高考数学第一轮复习精练检测试题立体几何 17页

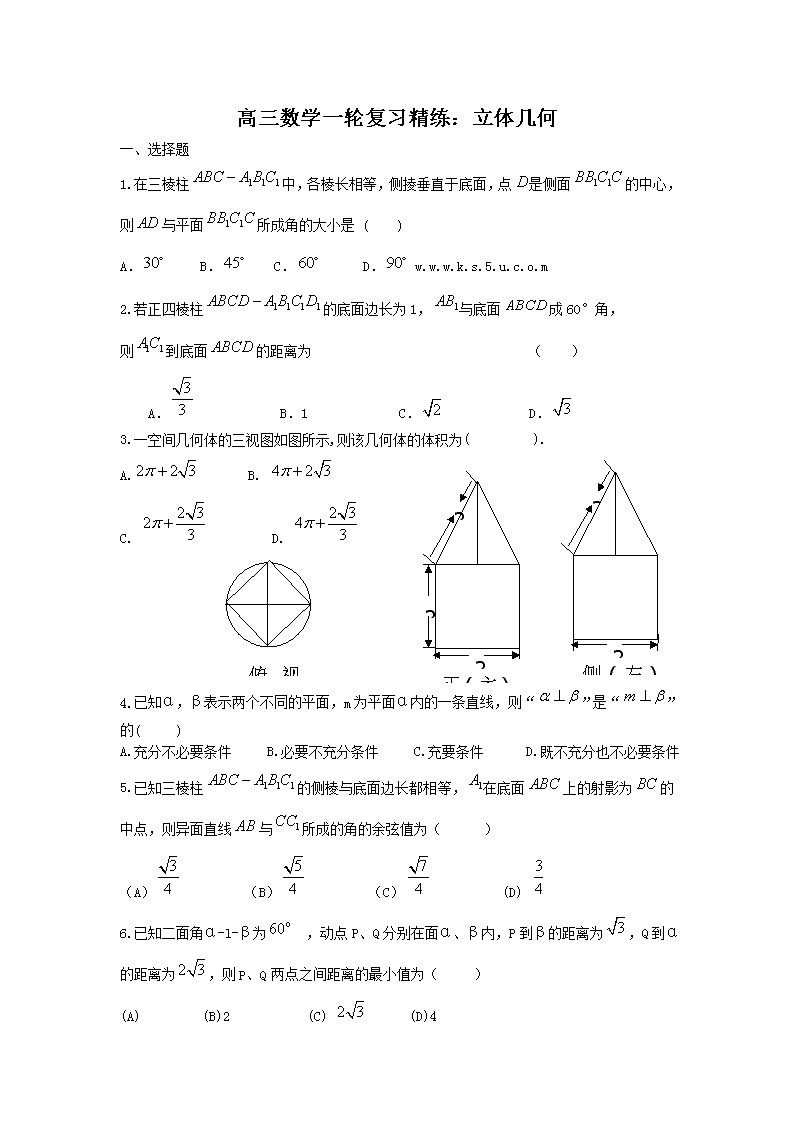
高三数学一轮复习精练：立体几何 一、选择题 ‎1.在三棱柱中，各棱长相等，侧掕垂直于底面，点是侧面的中心，则与平面所成角的大小是 ( )‎ A． B． C． D． w.w.w.k.s.5.u.c.o.m ‎ ‎2.若正四棱柱的底面边长为1，与底面成60°角，‎ 则到底面的距离为 （ ）‎ ‎ A． B．‎1 C． D．‎ ‎3.一空间几何体的三视图如图所示,则该几何体的体积为( ).‎ ‎2 ‎ ‎2 ‎ 侧(左)视图 ‎ ‎2 ‎ ‎2 ‎ ‎2 ‎ 正(主)视图 ‎ A. B. ‎ C. D. ‎ 俯视图 ‎ ‎4.已知α，β表示两个不同的平面，m为平面α内的一条直线，则“”是“”的( )‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎ ‎5.已知三棱柱的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为（ ）‎ ‎（A） （B） （C） (D) ‎ ‎6.已知二面角α-l-β为 ，动点P、Q分别在面α、β内，P到β的距离为，Q到α的距离为，则P、Q两点之间距离的最小值为（ ）‎ ‎(A) (B)2 (C) (D)4 ‎ ‎7.已知正四棱柱中，为中点，则异面直线与所成的角的余弦值为 ( )‎ ‎ A. B. C. D. ‎ ‎8.如图，正方体的棱线长为1，线段上有两个动点E，F，且，则下列结论中错误的是 ‎ ‎（A）‎ ‎（B）‎ ‎（C）三棱锥的体积为定值 ‎（D）异面直线所成的角为定值 ‎9.平面六面体中，既与共面也与共面的棱的条数为（ ）‎ A．3 B．‎4 C．5 D．6 ‎ ‎10.如图，已知六棱锥的底面是正六边形，，则下列结论正确的是 Ａ.　　 ‎ Ｂ.平面 ‎ C. 直线∥平面 Ｄ.‎ ‎11.如图，在半径为3的球面上有三点，，球心到平面的距离是，则两点的球面距离是 ( )‎ A. B. C. D. 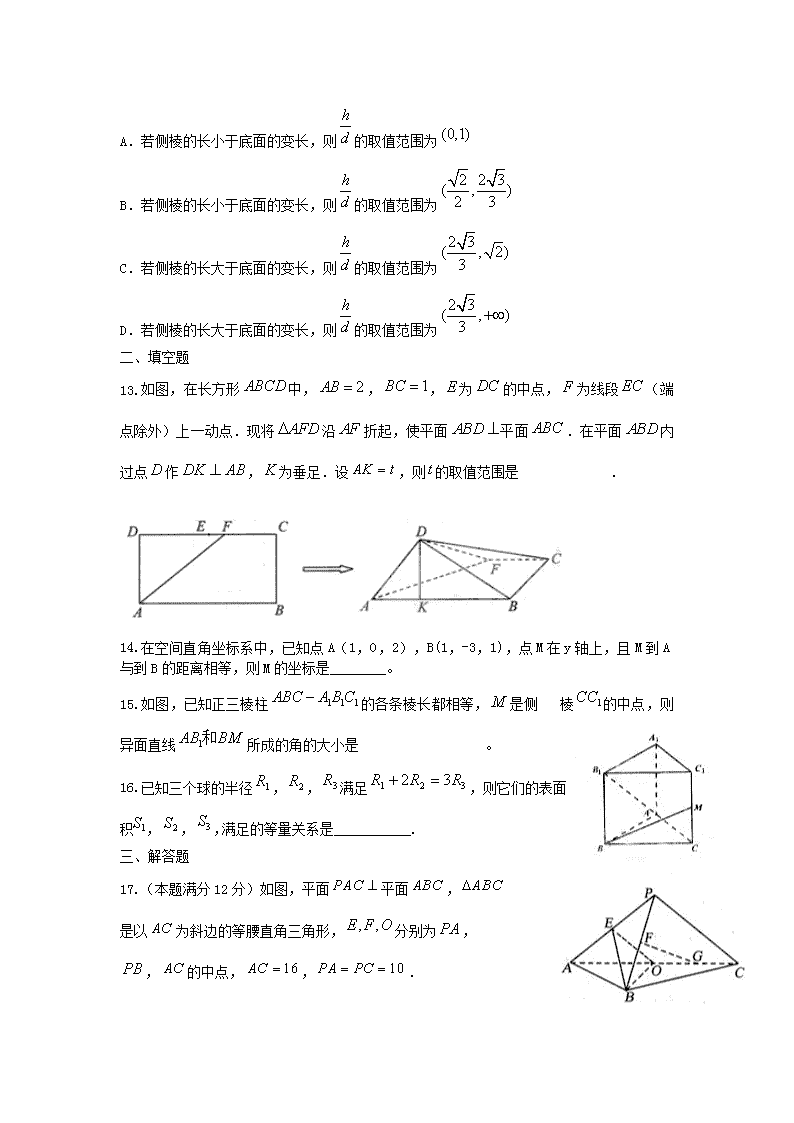‎ ‎12.在正四棱柱中，顶点到对角线和到平面的距离分别为和，则下列命题中正确的是（ ）‎ A．若侧棱的长小于底面的变长，则的取值范围为 B．若侧棱的长小于底面的变长，则的取值范围为 C．若侧棱的长大于底面的变长，则的取值范围为 D．若侧棱的长大于底面的变长，则的取值范围为 二、填空题 ‎13.如图，在长方形中，，，为的中点，为线段（端点除外）上一动点．现将沿折起，使平面平面．在平面内过点作，为垂足．设，则的取值范围是 ．‎ ‎14.在空间直角坐标系中，已知点A（1，0，2），B(1，-3，1)，点M在y轴上，且M到A与到B的距离相等，则M的坐标是________。‎ ‎15.如图，已知正三棱柱的各条棱长都相等，是侧 棱的中点，则异面直线所成的角的大小是 。 ‎ ‎16.已知三个球的半径，，满足，则它们的表面积，，，满足的等量关系是___________. ‎ 三、解答题 ‎17.（本题满分12分）如图，平面平面，‎ 是以为斜边的等腰直角三角形，分别为，‎ ‎，的中点，，．‎ ‎ （I）设是的中点，证明：平面；‎ ‎ （II）证明：在内存在一点，使平面，并求点到，的距离．‎ ‎18.（本小题共14分）‎ 如图，四棱锥的底面是正方形，，点E在棱PB上.‎ ‎（Ⅰ）求证：平面； ‎ ‎（Ⅱ）当且E为PB的中点时，求AE与平面PDB所成的角的大小.‎ ‎19.（本小题共14分）‎ ‎ 如图，在三棱锥中，底面，‎ 点，分别在棱上，且 ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）当为的中点时，求与平面所成的角的大小；‎ ‎（Ⅲ）是否存在点使得二面角为直二面角？并说明理由.‎ ‎20.（本小题满分12分）‎ 如图，在四棱锥中，底面是矩形，平面，，．以的中点为球心、为直径的球面交于点．‎ ‎（1）求证：平面⊥平面；‎ ‎（2）求直线与平面所成的角；w.w.w.k.s.5.u.c.o.m ‎ ‎（3）求点到平面的距离．‎ ‎21.（本小题满分12分）‎ 如图，正方形所在平面与平面四边形所在平面互相垂直，△‎ 是等腰直角三角形，‎ ‎（I）求证：；‎ ‎（II）设线段、的中点分别为、，求证： ∥‎ ‎（III）求二面角的大小。‎ ‎22.（本小题满分12分）‎ ‎ 如图，四棱锥S＝ABCD的底面是正方形，SD⊥平面ABCD,SD＝AD＝a,点E是SD上的点，且DE＝a(0<≦1). ‎ ‎(Ⅰ)求证：对任意的（0、1），都有AC⊥BE:‎ ‎(Ⅱ)若二面角C-AE-D的大小为‎600C，求的值。‎ 参考答案 ‎1.【答案】：C ‎ ‎【解析】：取BC的中点E，则面，w.w.w.k.s.5.u.c.o.m ‎ ‎，因此与平面所成角即为，设，则，，即有．‎ ‎2.【答案】D ‎【解析】本题主要考查正四棱柱的概念、‎ 直线与平面所成的角以及直线与平面的距离等概念（第4题解答图）‎ 属于基础知识、基本运算的考查.‎ ‎ 依题意，，如图，‎ ‎，故选D.‎ ‎3.【答案】:C ‎【解析】:该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为,四棱锥的底面边长为，高为，所以体积为 所以该几何体的体积为.‎ ‎【命题立意】:本题考查了立体几何中的空间想象能力,‎ 由三视图能够想象得到空间的立体图,并能准确地w.w.w.k.s.5.u.c.o.m ‎ 计算出.几何体的体积.‎ ‎4.【答案】:B.‎ ‎【解析】:由平面与平面垂直的判定定理知如果m为平面α内的一条直线,,则,反过来则不一定.所以“”是“”的必要不充分条件 .‎ ‎【命题立意】:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.‎ ‎5.【答案】：D ‎【解析】：设的中点为D，连结D，AD，易知即为异面直线 与所成的角,由三角余弦定理，‎ 易知.故选D ‎ ‎6.【答案】：C ‎【解析】:如图分别作 ‎ ‎，连 ‎，‎ 又 当且仅当，即重合时取最小值。‎ ‎7.【答案】：C ‎【解析】：令则,连∥ 异面直线与所成的角即与所成的角。在中由余弦定理易得。‎ ‎8.【答案】：D ‎【解析】：A正确，‎ 易证B显然正确，；C正确，可用等积法求得；D错误。.‎ ‎9.【答案】：C ‎【解析】:如图，用列举法知合要求的棱为：、、、、，‎ ‎10.【答案】：D ‎【考点定位】本小题考查空间里的线线、线面关系，基础题。（同文6）‎ 解：由三垂线定理，因AD与AB不相互垂直，排除A；作于，‎ 因面面ABCDEF，而AG在面ABCDEF上的射影在AB上，而AB与BC不相互垂直，故排除B；由，而EF是平面PAE的斜线，故排除C，故选择D。‎ 解析2：设低面正六边形边长为，则，由平面可知，且，所以在中有直线与平面所成的角为 ‎，故应选D。‎ ‎11.【答案】：B ‎【考点定位】本小题考查球的截面圆性质、球面距，基础题。（同文9）‎ ‎【解析】：由知截面圆的半径 ‎，故，所以两点的球面距离为，故选择B。w.w.w.k.s.5.u.c.o.m ‎ 解析2：过球心作平面的垂线交平面与，，则在直线上，由于，，所以，由为等腰直角三角形可得，所以为等边三角形，则两点的球面距离是。‎ ‎12.【答案】：C ‎【解析】：设底面边长为1，侧棱长为，过作。‎ 在中，，由三角形面积关系得w.w.w.k.s.5.u.c.o.m ‎ 设在正四棱柱中，由于，‎ 所以平面，于是，所以平面，故为点到平面 的距离，在中，又由三角形面积关系得于是，于是当，所以，所以 二、填空题（4题，每题5分）‎ ‎13.【答案】： ‎ ‎ 【解析】此题的破解可采用二个极端位置法，即对于F位于DC的中点时，，随着F点到C点时，因平面，即有，对于 ‎，又，因此有，则有，因此的取值范围是 w.w.w.k.s.5.u.c.o.m ‎ ‎14.【答案】(0,-1，0) w.w.w.k.s.5.u.c.o.m ‎ ‎【解析】设由可得故 ‎15.【答案】：。‎ ‎【考点定位】本小题考查异面直线的夹角，基础题。‎ ‎【解析】：不妨设棱长为2，选择基向量，则w.w.w.k.s.5.u.c.o.m ‎ ‎，故填写。‎ 法2：取BC中点N，连结，则面，∴是在面上的射影，由几何知识知，由三垂线定理得，故填写。‎ ‎16.【答案】‎ ‎【解析】，，同理：，即R1＝，R2＝，R3＝，由得 三．解答题（6题，共70分）‎ ‎17.证明：（I）如图，连结OP，以O为坐标原点，分别以OB、OC、OP所在直线为轴，轴，轴，建立空间直角坐标系O，w.w.w.k.s.5.u.c.o.m ‎ 则，由题意得，因，因此平面BOE的法向量为 ‎，得，又直线不在平面内，因此有平面 ‎（II）设点M的坐标为，则，因为平面BOE，所以有，因此有，即点M的坐标为，在平面直角坐标系中，的内部区域满足不等式组，经检验，点M的坐标满足上述不等式组，所以在内存在一点，使平面，由点M的坐标得点到，的距离为．w.w.w.k.s.5.u.c.o.m ‎ ‎18.【解法1】本题主要考查直线和平面垂直、平面与平面垂直、直线与平面所成的角等基础知识，考查空间想象能力、运算能力和推理论证能力．‎ ‎（Ⅰ）∵四边形ABCD是正方形，∴AC⊥BD，‎ ‎∵，‎ ‎∴PD⊥AC，∴AC⊥平面PDB，‎ ‎∴平面.‎ ‎（Ⅱ）设AC∩BD=O，连接OE，‎ ‎ 由（Ⅰ）知AC⊥平面PDB于O，‎ ‎ ∴∠AEO为AE与平面PDB所的角，‎ ‎ ∴O，E分别为DB、PB的中点，‎ ‎ ∴OE//PD，，又∵，‎ ‎ ∴OE⊥底面ABCD，OE⊥AO，‎ ‎ 在Rt△AOE中，，‎ ‎ ∴，即AE与平面PDB所成的角的大小为.‎ ‎【解法2】如图，以D为原点建立空间直角坐标系，‎ ‎ 设 则，‎ ‎（Ⅰ）∵，‎ ‎∴，‎ ‎∴AC⊥DP，AC⊥DB，∴AC⊥平面PDB，‎ ‎∴平面.‎ ‎（Ⅱ）当且E为PB的中点时，，‎ ‎ 设AC∩BD=O，连接OE， ‎ ‎ 由（Ⅰ）知AC⊥平面PDB于O，‎ ‎ ∴∠AEO为AE与平面PDB所的角，‎ ‎ ∵，‎ ‎∴，‎ ‎∴，即AE与平面PDB所成的角的大小为.‎ ‎19.【解法1】本题主要考查直线和平面垂直、直线与平面所成的角、二面角等基础知识，考查空间想象能力、运算能力和推理论证能力．‎ ‎（Ⅰ）∵PA⊥底面ABC，∴PA⊥BC.‎ 又，∴AC⊥BC.‎ ‎∴BC⊥平面PAC.‎ ‎（Ⅱ）∵D为PB的中点，DE//BC，‎ ‎∴，‎ 又由（Ⅰ）知，BC⊥平面PAC，w.w.w.k.s.5.u.c.o.m ‎ ‎∴DE⊥平面PAC，垂足为点E.‎ ‎∴∠DAE是AD与平面PAC所成的角，‎ ‎∵PA⊥底面ABC，∴PA⊥AB，又PA=AB，‎ ‎∴△ABP为等腰直角三角形，∴，‎ ‎∴在Rt△ABC中，，∴.‎ ‎∴在Rt△ADE中，，‎ ‎∴与平面所成的角的大小.‎ ‎（Ⅲ）∵AE//BC，又由（Ⅰ）知，BC⊥平面PAC，∴DE⊥平面PAC，‎ 又∵AE平面PAC，PE平面PAC，∴DE⊥AE，DE⊥PE，‎ ‎∴∠AEP为二面角的平面角，‎ ‎∵PA⊥底面ABC，∴PA⊥AC，∴.‎ ‎∴在棱PC上存在一点E，使得AE⊥PC，这时，‎ 故存在点E使得二面角是直二面角.‎ ‎【解法2】如图，以A为原煤点建立空间直角坐标系，‎ ‎ 设，由已知可得 ‎ .‎ ‎ （Ⅰ）∵， ∴，∴BC⊥AP.‎ 又∵，∴BC⊥AC，∴BC⊥平面PAC.‎ ‎（Ⅱ）∵D为PB的中点，DE//BC，∴E为PC的中点，‎ ‎∴，‎ ‎∴又由（Ⅰ）知，BC⊥平面PAC，∴∴DE⊥平面PAC，垂足为点E.‎ ‎∴∠DAE是AD与平面PAC所成的角，‎ ‎∵，‎ ‎∴.‎ ‎∴与平面所成的角的大小. w.w.w.k.s.5.u.c.o.m ‎ ‎（Ⅲ）同解法1.‎ ‎20.解：方法（一）：‎ ‎（1）证：依题设，Ｍ在以ＢＤ为直径的球面上，则ＢＭ⊥ＰＤ.‎ 因为ＰＡ⊥平面ＡＢＣＤ，则ＰＡ⊥ＡＢ，又ＡＢ⊥ＡＤ，‎ 所以ＡＢ⊥平面ＰＡＤ，则ＡＢ⊥ＰＤ，因此有ＰＤ⊥平面ＡＢＭ，所以平面ＡＢＭ⊥平面ＰＣＤ.‎ ‎（２）设平面ＡＢＭ与ＰＣ交于点Ｎ，因为ＡＢ∥ＣＤ，所以ＡＢ∥平面ＰＣＤ，则ＡＢ∥ＭＮ∥ＣＤ，‎ 由（1）知，ＰＤ⊥平面ＡＢＭ，则MN是PN在平面ABM上的射影，‎ 所以 就是与平面所成的角，‎ 且 ‎ 所求角为 ‎（3）因为O是BD的中点，则O点到平面ABM的距离等于D点到平面ABM距离的一半，由（1）知，ＰＤ⊥平面ＡＢＭ于M，则|DM|就是D点到平面ABM距离.‎ 因为在Rt△PAD中，，，所以为中点，，则O点到平面ABM的距离等于。‎ 方法二：‎ ‎（1）同方法一；‎ ‎（2）如图所示，建立空间直角坐标系，则，，， ，，，‎ 设平面的一个法向量，由可得：，令，则，即.设所求角为，则，‎ 所求角的大小为. ‎ ‎（3）设所求距离为，由，得：‎ ‎21.【解析】解法一：‎ 因为平面ABEF⊥平面ABCD，BC平面ABCD，BC⊥AB，平面ABEF∩平面ABCD=AB，‎ 所以BC⊥平面ABEF.‎ 所以BC⊥EF.‎ 因为⊿ABE为等腰直角三角形，AB=AE，‎ 所以∠AEB=45°，‎ 又因为∠AEF=45,‎ 所以∠FEB=90°，即EF⊥BE.‎ 因为BC平面ABCD, BE平面BCE, w.w.w.k.s.5.u.c.o.m ‎ BC∩BE=B 所以…………………6分 ‎（II）取BE的中点N,连结CN,MN,则MNPC ‎∴ PMNC为平行四边形,所以PM∥CN.‎ ‎∵ CN在平面BCE内,PM不在平面BCE内,‎ ‎∴ PM∥平面BCE. …………………………………………8分 ‎（III）由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.‎ 作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,‎ 作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.‎ ‎∴ ∠FHG为二面角F-BD-A的平面角.‎ ‎∵ FA=FE,∠AEF=45°,‎ ‎∠AEF=90°, ∠FAG=45°.‎ 设AB=1,则AE=1,AF=,则 在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+=, w.w.w.k.s.5.u.c.o.m ‎ ‎, ‎ 在Rt⊿FGH中, ,‎ ‎∴ 二面角的大小为……………………………12分 ‎ 解法二: 因等腰直角三角形，，所以 又因为平面，所以⊥平面，‎ 所以 即两两垂直；如图建立空间直角坐标系,‎ ‎ (I) 设，则，‎ ‎∵，∴，‎ 从而 ‎ ‎，‎ 于是，‎ ‎ ∴⊥,⊥‎ ‎ ∵平面，平面， ∴‎ ‎（II），从而 ‎ 于是 ‎ ∴⊥，又⊥平面，直线不在平面内，‎ ‎ 故∥平面 ‎（III）设平面的一个法向量为，并设＝（‎ ‎ ‎ ‎ 即 w.w.w.k.s.5.u.c.o.m ‎ ‎ 取，则，，从而＝（1，1，3）‎ 取平面D的一个法向量为 ‎ ，故二面角的大小为 ‎22.本小题主要考察空间直线与直线、直线与平面的位置关系和二面角等基础知识，考查空间想象能力、推理论证能力和运算求解能力。（满分12分）‎ ‎ （Ⅰ）证发1：连接BD，由底面是正方形可得ACBD。‎ ‎ SD平面ＡＢＣＤ，BD是BE在平面ABCD上的射影，‎ 由三垂线定理得ACBE.‎ ‎(II)解法1：SD平面ABCD，ＣＤ平面ＡＢＣＤ， SDCD. ‎ 又底面ＡＢＣＤ是正方形， ＣDＡD，又ＳＤAD=D，CD平面SAD。‎ 过点D在平面SAD内做DFAE于F，连接CF，则CFAE， ‎ 故CFD是二面角C-AE-D 的平面角，即CFD=60°‎ 在Rt△ADE中，AD=, DE= ， AE= 。‎ 于是，DF=‎ 在Rt△CDF中，由cot60°=‎ 得， 即=3 ‎ ‎， 解得=‎