高考常用24个物理模型 23页

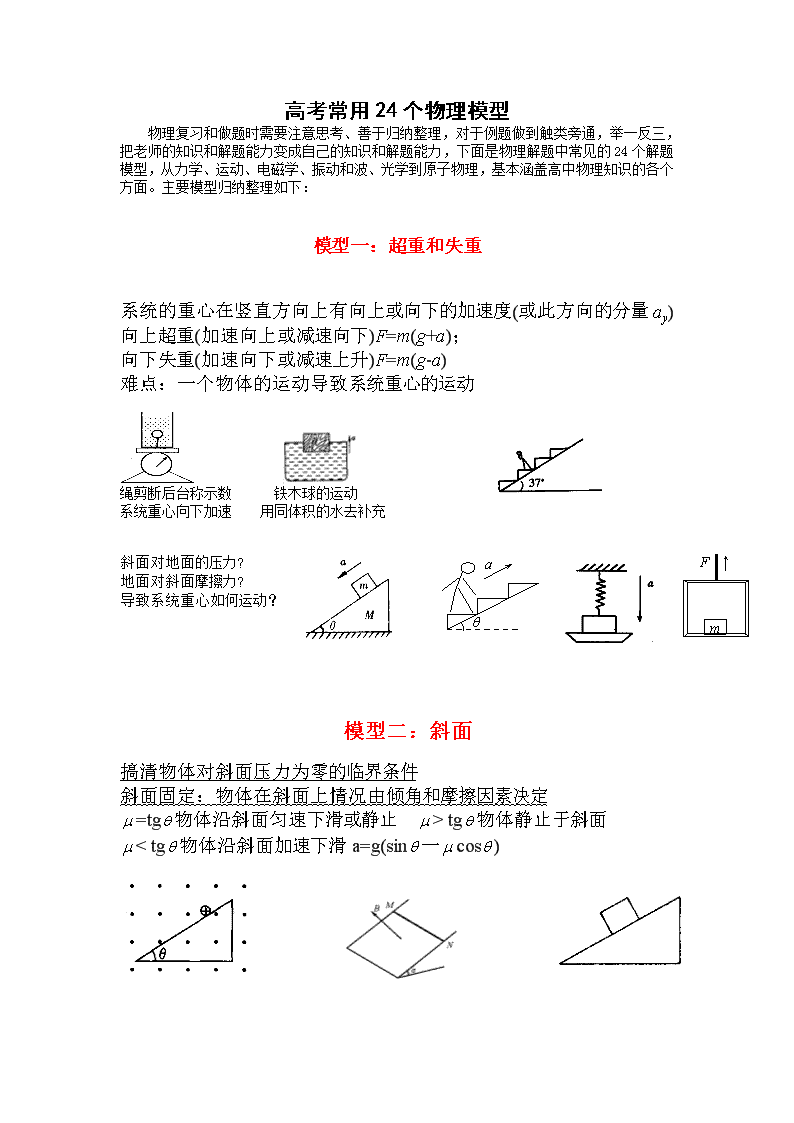
高考常用24个物理模型 物理复习和做题时需要注意思考、善于归纳整理，对于例题做到触类旁通，举一反三，把老师的知识和解题能力变成自己的知识和解题能力，下面是物理解题中常见的24个解题模型，从力学、运动、电磁学、振动和波、光学到原子物理，基本涵盖高中物理知识的各个方面。主要模型归纳整理如下：‎ 模型一：超重和失重 系统的重心在竖直方向上有向上或向下的加速度(或此方向的分量ay)‎ 向上超重(加速向上或减速向下)F=m(g+a)；‎ 向下失重(加速向下或减速上升)F=m(g-a)‎ 难点：一个物体的运动导致系统重心的运动 ‎ ‎ ‎ ‎ 绳剪断后台称示数 铁木球的运动 ‎ 系统重心向下加速 用同体积的水去补充 ‎ ‎ a q F m 斜面对地面的压力? ‎ 地面对斜面摩擦力? ‎ 导致系统重心如何运动？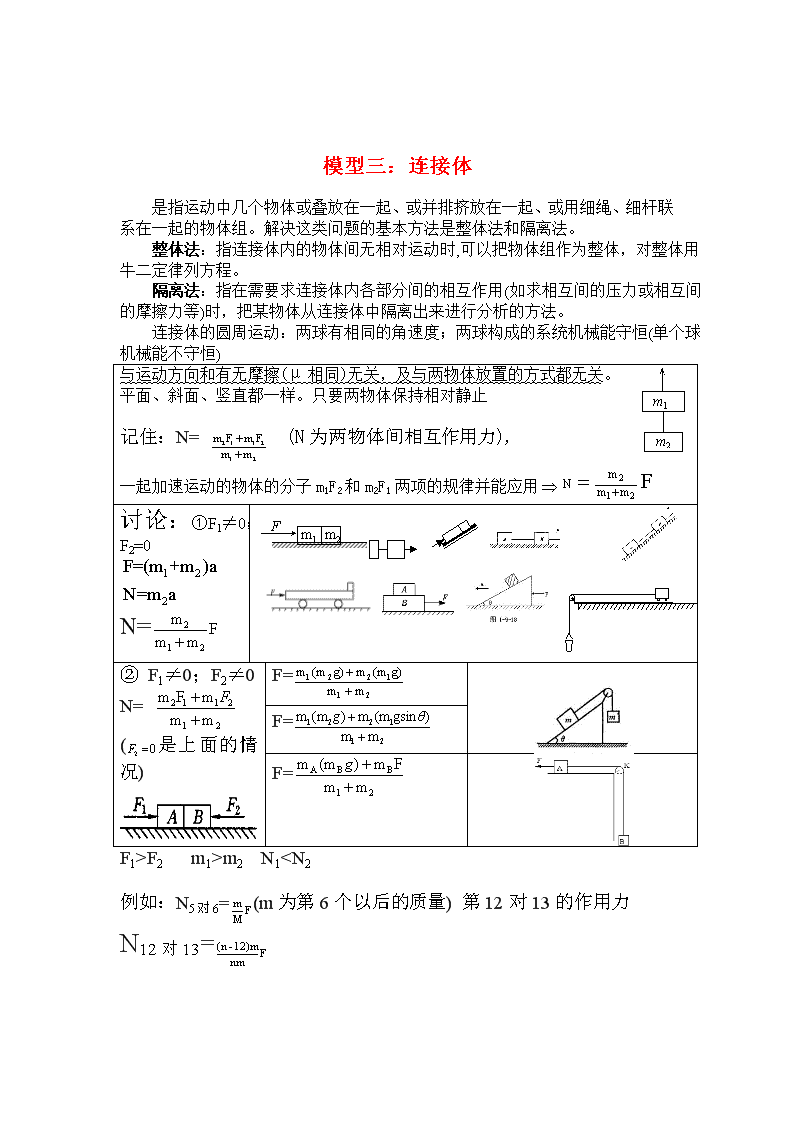‎ ‎ ‎ ‎ 模型二：斜面 搞清物体对斜面压力为零的临界条件 斜面固定：物体在斜面上情况由倾角和摩擦因素决定 ‎=tg物体沿斜面匀速下滑或静止 > tg物体静止于斜面 ‎< tg物体沿斜面加速下滑a=g(sin一cos) ‎ ‎ ‎ 模型三：连接体 是指运动中几个物体或叠放在一起、或并排挤放在一起、或用细绳、细杆联系在一起的物体组。解决这类问题的基本方法是整体法和隔离法。‎ ‎ 整体法：指连接体内的物体间无相对运动时,可以把物体组作为整体，对整体用牛二定律列方程。‎ ‎ 隔离法：指在需要求连接体内各部分间的相互作用(如求相互间的压力或相互间的摩擦力等)时，把某物体从连接体中隔离出来进行分析的方法。‎ ‎ 连接体的圆周运动：两球有相同的角速度；两球构成的系统机械能守恒(单个球机械能不守恒)‎ m1‎ m2‎ 与运动方向和有无摩擦(μ相同)无关，及与两物体放置的方式都无关。‎ 平面、斜面、竖直都一样。只要两物体保持相对静止 记住：N= (N为两物体间相互作用力), ‎ 一起加速运动的物体的分子m1F2和m2F1两项的规律并能应用 讨论：①F1≠0；F2=0‎ ‎ N=‎ m2‎ m1‎ F ‎② F1≠0；F2≠0‎ N= ‎ ‎(是上面的情况)‎ F=‎ F=‎ F=‎ F1>F2 m1>m2 N1 VB=‎ ‎ 所以AB杆对B做正功，AB杆对A做负功 ◆ 通过轻绳连接的物体 ‎①在沿绳连接方向(可直可曲)，具有共同的v和a。‎ 特别注意：两物体不在沿绳连接方向运动时，先应把两物体的v和a在沿绳方向分解，求出两物体的v和a的关系式，‎ ‎②被拉直瞬间，沿绳方向的速度突然消失，此瞬间过程存在能量的损失。‎ 讨论：若作圆周运动最高点速度 V0<，运动情况为先平抛，绳拉直时沿绳方向的速度消失。‎ ‎ 即是有能量损失，绳拉紧后沿圆周下落机械能守恒。而不能够整个过程用机械能守恒。‎ ‎ 自由落体时，在绳瞬间拉紧(沿绳方向的速度消失)有能量损失(即v1突然消失)，再v2下摆机械能守恒 ‎ ‎ 模型五：上抛和平抛 ‎1．竖直上抛运动：速度和时间的对称 ‎ ‎ 分过程：上升过程匀减速直线运动,下落过程初速为0的匀加速直线运动.‎ 全过程：是初速度为V0加速度为-g的匀减速直线运动。‎ ‎(1)上升最大高度:H=V0²/2g (2)上升的时间 t=V0/g ‎ (3)从抛出到落回原位置的时间:t =2‎ ‎ (4)上升、下落经过同一位置时的加速度相同，而速度等值反向 ‎ ‎(5)上升、下落经过同一段位移的时间相等。‎ ‎(6)匀变速运动适用全过程S = Vo t －g t2 ; Vt = Vo－g t ; ‎ Vt2－Vo2 = －2gS (S、Vt的正负号的理解)‎ ‎2.平抛运动：匀速直线运动和初速度为零的匀加速直线运动的合运动 ‎（1）运动特点：a、只受重力；b、初速度与重力垂直。其运动的加速度却恒为重力加速度g，是一个匀变速曲线运动，在任意相等时间内速度变化相等。‎ ‎（2）平抛运动的处理方法：可分解为水平方向的匀速直线运动和竖直方向的自由落体运动，两个分运动既具有独立性又具有等时性。‎ ‎（3）平抛运动的规律：做平抛运动的物体，任意时刻速度的反向延长线一定经过此时沿抛出方向水平总位移的中点。‎ 证：平抛运动示意如图，设初速度为V0，某时刻运动到A点，位置坐标为(x,y ),所用时间为t.此时速度与水平方向的夹角为,速度的反向延长线与水平轴的交点为,位移与水平方向夹角为.以物体的出发点为原点，沿水平和竖直方向建立坐标。‎ 依平抛规律有: ‎ ‎ Vx= V0 ‎ 速度： Vy=gt ‎ ‎ ① ‎ ‎ Sx= Vot ‎ 位移: ‎ ‎ ②‎ ‎ 由①②得： 即 ③‎ ‎ 所以: ④‎ ‎④式说明：做平抛运动的物体，任意时刻速度的反向延长线一定经过此时沿抛出方向水总位移的中点。‎ 模型六：水流星 (竖直平面圆周运动)‎ ‎◆变速圆周运动 研究物体通过最高点和最低点的情况，并且经常出现临界状态。(圆周运动实例) ‎ ‎ ①火车转弯 ‎ ‎②汽车过拱桥、凹桥3‎ ‎③飞机做俯冲运动时，飞行员对座位的压力。‎ ‎④物体在水平面内的圆周运动（汽车在水平公路转弯，水平转盘上的物体，绳拴着的物体在光滑水平面上绕绳的一端旋转）和物体在竖直平面内的圆周运动（翻滚过山车、水流星、杂技节目中的飞车走壁等）。‎ ‎⑤万有引力——卫星的运动、库仑力——电子绕核旋转、洛仑兹力——带电粒子在匀强磁场中的偏转、重力与弹力的合力——锥摆、（关健要搞清楚向心力怎样提供的）‎ （1） 火车转弯：‎ 设火车弯道处内外轨高度差为h，内外轨间距L，转弯半径R。由于外轨略高于内轨，使得火车所受重力和支持力的合力F合提供向心力。‎ ‎ ‎ ‎(是内外轨对火车都无摩擦力的临界条件)‎ 火车提速靠增大轨道半径或倾角来实现 （2） 无支承的小球：‎ 在竖直平面内作圆周运动过最高点情况：‎ 受力：由mg+T=mv2/L知,小球速度越小,绳拉力或环压力T越小,T最小值只能为零,此时小球重力作向心力。‎ 结论：最高点时绳子(或轨道)对小球没有力的作用，此时只有重力提供作向心力。‎ ‎ 能过最高点条件：V≥V临（当V≥V临时，绳、轨道对球分别产生拉力、压力）‎ ‎ 不能过最高点条件：V RX 适于测大电阻 Rx >‎ 外 A V R小 ‎　‎ R测=n倍的Rx 通电前调到最大 调压 ‎0～E ‎　0～‎ 电压变化范围大 要求电压 从0开始变化 Rx比较大、R滑 比较小 R滑全>Rx/2‎ 通电前调到最小 R滑唯一：比较R滑与Rx 控制电路 ‎ Rx