历年高考数学试题极坐标与参数方程 7页

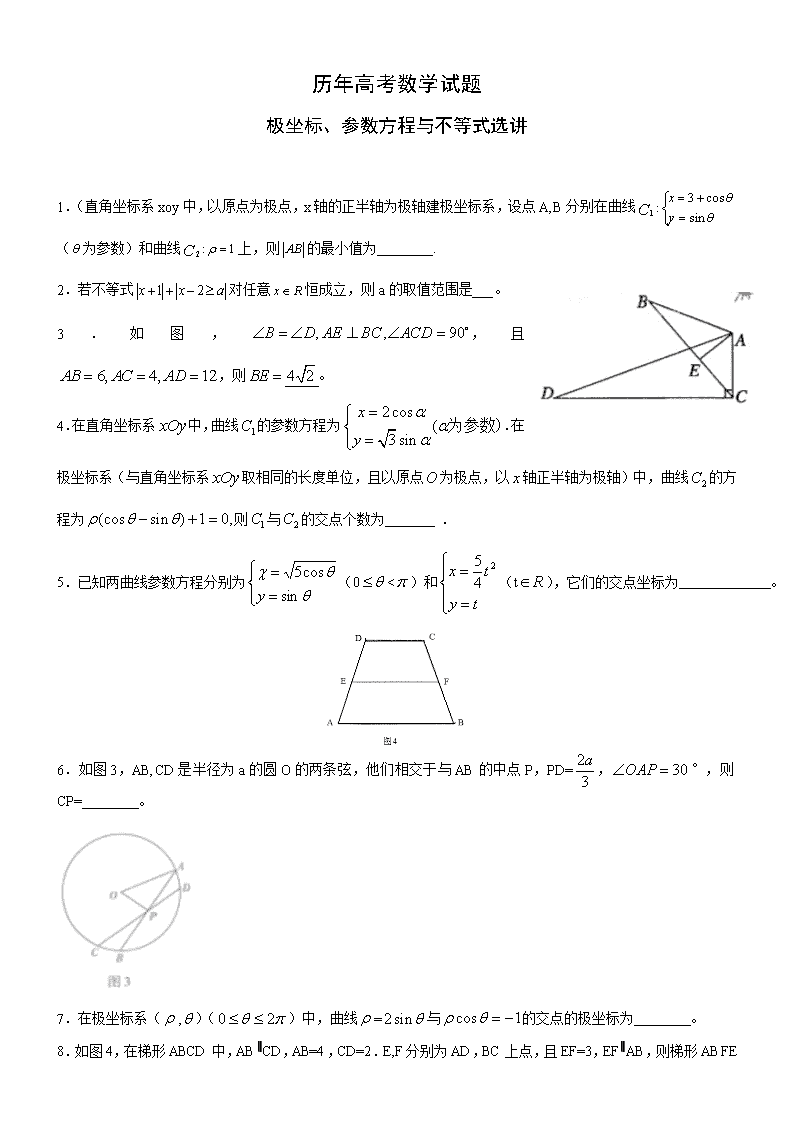
历年高考数学试题 极坐标、参数方程与不等式选讲 ‎1．（直角坐标系xoy中，以原点为极点，x轴的正半轴为极轴建极坐标系，设点A,B分别在曲线 （为参数）和曲线上，则的最小值为________.‎ ‎2．若不等式对任意恒成立，则a的取值范围是___。‎ ‎3．如图，，且，则。‎ ‎4．在直角坐标系中，曲线的参数方程为．在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，曲线的方程为则与的交点个数为 ．‎ ‎5．已知两曲线参数方程分别为（0<）和（t），它们的交点坐标为 。‎ ‎6．如图3，AB,CD是半径为a的圆O的两条弦，他们相交于与AB的中点P，PD=，°，则CP= 。‎ ‎7．在极坐标系（,）（）中，曲线=与的交点的极坐标为 。‎ ‎8．如图4，在梯形ABCD中，AB∥CD，AB=4，CD=2．E,F分别为AD，BC上点，且EF=3，EF∥AB，则梯形ABFE 与梯形EFCD的面积比为 。‎ ‎9．已知抛物线的参数方程为（为参数）若斜率为1的直线经过抛物线的焦点，且与圆相切，则=________.‎ ‎10．在极坐标系中，直线与直线的夹角大小为 。‎ ‎11．若关于的不等式存在实数解，则实数的取值范围是 。‎ ‎12．直角坐标系中，以原点为极点，轴的正半轴为极轴建立极坐标系，设点A，B分别在曲线（为参数）和曲线上，则的最小值为 3 。‎ ‎13.在直角坐标系中，曲线C1的参数方程为（为参数）在极坐标系（与直角坐标系取相同的长度单位，且以原点O为极点，以轴正半轴为极轴）中，曲线的方程为，则与的交点个数为 。 ‎ ‎14.设,则的最小值为 。‎ ‎16.如图2，是半圆周上的两个三等分点，直径，,垂足为D, 与相交与点F，则的长为 。‎ ‎17.已知两面线参数方程分别为 和，它们的交点坐标为___________.‎ ‎18．如图4，过圆外一点分别作圆的切线和割线交圆于,，且=7，是圆上一点使得=5，∠=∠, 则= 。‎ ‎19．在平面直角坐标系xOy中，曲线C1的参数方程为（为参数），‎ 曲线C2的参数方程为（，为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=与C1，C2各有一个交点．当=0时，这两个交点间的距离为2，当=时，这两个交点重合．‎ ‎（I）分别说明C1，C2是什么曲线，并求出a与b的值；‎ ‎（II）设当=时，l与C1，C2的交点分别为A1，B1，当=时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．‎ ‎20．已知函数=|x-2|x-5|．‎ ‎（I）证明：≤≤3；‎ ‎（II）求不等式≥x2x+15的解集．‎ ‎21．如图，，分别为的边，上的点，且不与的顶点重合。已知的长为，，的长是关于的方程的两个根。‎ ‎（Ⅰ）证明：，，，四点共圆；‎ ‎（Ⅱ）若，且，求，，，所在圆的半径。‎ ‎22．在直角坐标系xOy 中，曲线C1的参数方程为（为参数），M是C1上的动点，P点满足,P点的轨迹为曲线C2‎ ‎(Ⅰ)求C2的方程 ‎(Ⅱ)在以O为极点，x轴的正半轴为极轴的极坐标系中，射线与C1的异于极点的交点为A，与C2的异于极点的交点为B，求.‎ ‎23．设函数,其中。‎ ‎（Ⅰ）当时，求不等式的解集 ‎（Ⅱ）若不等式的解集为，求a的值。‎ ‎24．如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC=ED．‎ ‎（I）证明：CD//AB；‎ ‎（II）延长CD到F，延长DC到G，使得EF=EG，证明：A，B，G，F四点共圆．‎ ‎25．在平面直角坐标系xOy中，曲线C1的参数方程为（为参数），曲线C2的参数方程 为（，为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=与C1，C2各有一个交点．当=0时，这两个交点间的距离为2，当=时，这两个交点重合．‎ ‎（I）分别说明C1，C2是什么曲线，并求出a与b的值；‎ ‎（II）设当=时，l与C1，C2的交点分别为A1，B1，当=时，l与C1，C2的交点为A2，B2，求四边形A‎1A2B2B1的面积．‎ ‎26．若曲线的极坐标方程为，以极点为原点，极轴为x轴正半轴建立直角坐标系，则改曲线的直角坐标方程为 .‎ ‎27．对于实数x，y，若，，则的最大值为 .‎ ‎28．设矩阵 （其中a＞0，b＞0）.‎ ‎（I）若a=2，b=3，求矩阵M的逆矩阵M-1；‎ ‎（II）若曲线C：x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’：，求a，b的值.‎ ‎29．在直接坐标系中，直线l的方程为x-y+4=0，曲线C的参数方程为.‎ ‎（I）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，），判断点P与直线l的位置关系；‎ ‎（II）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值.‎ ‎30．设不等式的解集为M.‎ ‎（I）求集合M；‎ ‎（II）若a，b∈M，试比较ab+1与a+b的大小.‎ ‎31．如图：已知圆上的弧，过C点的圆的切线与BA的延长线交于 E点，证明：‎ ‎（Ⅰ）=。‎ ‎（Ⅱ）=BE x CD。‎ ‎32．y=tsina y=‎ X=‎ 已知直线：{ {t为参数}。图：{ {为参数}‎ ‎（Ⅰ）当a=时，求与的交点坐标：‎ ‎（Ⅱ）过坐标原点O做的垂线，垂足为A、P为OA的中点，当a变化时，求P点轨迹的参数方程，并指出它是什么曲线。‎ ‎33．设函数。‎ ‎（Ⅰ）画出函数的图像： ‎ ‎（Ⅱ）若不等式的解集非空，求n的取值范围 ‎34．不等式的解集为 .‎ ‎35．如图，已知Rt△ABC的两条直角边AC，BC的长分别为‎3cm，‎4cm，以AC为直径的圆与AB交于点D，则BD＝ cm.‎ ‎36．参数方程（为参数）化成普通方程为 .‎ ‎37．已知为半圆（为参数，）上的点，点的坐标为，为坐标原点，点在射线上，线段与的弧的长度均为。‎ ‎（Ⅰ）以为极点，轴的正半轴为极轴建立极坐标系，求点的坐标；‎ ‎（Ⅱ）求直线的参数方程 ‎（38．已知均为正数，证明：，并确定为何值时，等号成立。‎ ‎39．AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，求证：AB=2BC。‎ ‎40．在平面直角坐标系xOy中，已知点A(0,0)，B(-2,0)，C(-2,1)。设k为非零实数，矩阵M=,N=，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B‎1C1的面积是△ABC面积的2倍，求k的值。‎ ‎41．在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切，求实数a的值。‎ ‎42．设a、b是非负实数，求证：。‎ ‎43．如图，已经圆上的弧，过C点的圆切线与BA的延长线交于E点，证明：‎ ‎（Ⅰ）∠ACE=∠BCD；‎ ‎（Ⅱ）BC2=BF×CD。‎ ‎44．已知直线C1（t为参数），C2（为参数），‎ ‎（Ⅰ）当=时，求C1与C2的交点坐标；‎ ‎（Ⅱ）过坐标原点O做C1的垂线，垂足为，P为OA中点，当变化时，求P点的轨迹的参数方程，并指出它是什么曲线。‎ ‎45．不等式的解集为 ‎46．如图，已知Rt△ABC的两条直角边AC,BC的长分别为‎3cm,‎4cm，以AC为直径的圆与AB交于点D，则 ‎47．已知圆C的参数方程为（a为参数）以原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为，则直线l与圆C的交点的直角坐标系为__(-1,1).(1,1)_____‎ ‎48．如图，的角平分线AD的延长线交它的外接圆于点E ‎（I）证明：‎ ‎（II）若的面积，求的大小。‎ ‎49．已知P为半圆C： （为参数，）上的点，点A的坐标为（1,0），‎ O为坐标原点，点M在射线OP上，线段OM与C的弧的长度均为。‎ ‎（I）以O为极点，轴的正半轴为极轴建立极坐标系，求点M的极坐标；‎ ‎（II）求直线AM的参数方程。‎ ‎50．已知均为正数，证明：，并确定为何值时，等号成立。‎ ‎51．已知矩阵M=，N=，且MN=。‎ ‎（Ⅰ）求实数a,b,c,d的值；‎ ‎（Ⅱ）求直线y=3x在矩阵M所对应的线性变换作用下的像的方程。‎ ‎52．在直角坐标系xOy中，直线L的参数方程为 （t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为=2sin。‎ ‎（Ⅰ）求圆C的直角坐标方程；‎ ‎（Ⅱ）设圆C与直线L交于点A,B。若点P的坐标为（3，），求∣PA∣+∣PB∣。‎ ‎53．已知函数f(x)=∣x-a∣.‎ ‎（Ⅰ）若不等式f(x)3的解集为，求实数a的值；‎ ‎（Ⅱ）在（Ⅰ）的条件下，若f(x)+f(x+5)≥m对一切实数x恒成立，求实数m的取值范围。‎