2015高考数学一轮方法测评练必考附加题——模板成形练2 5页

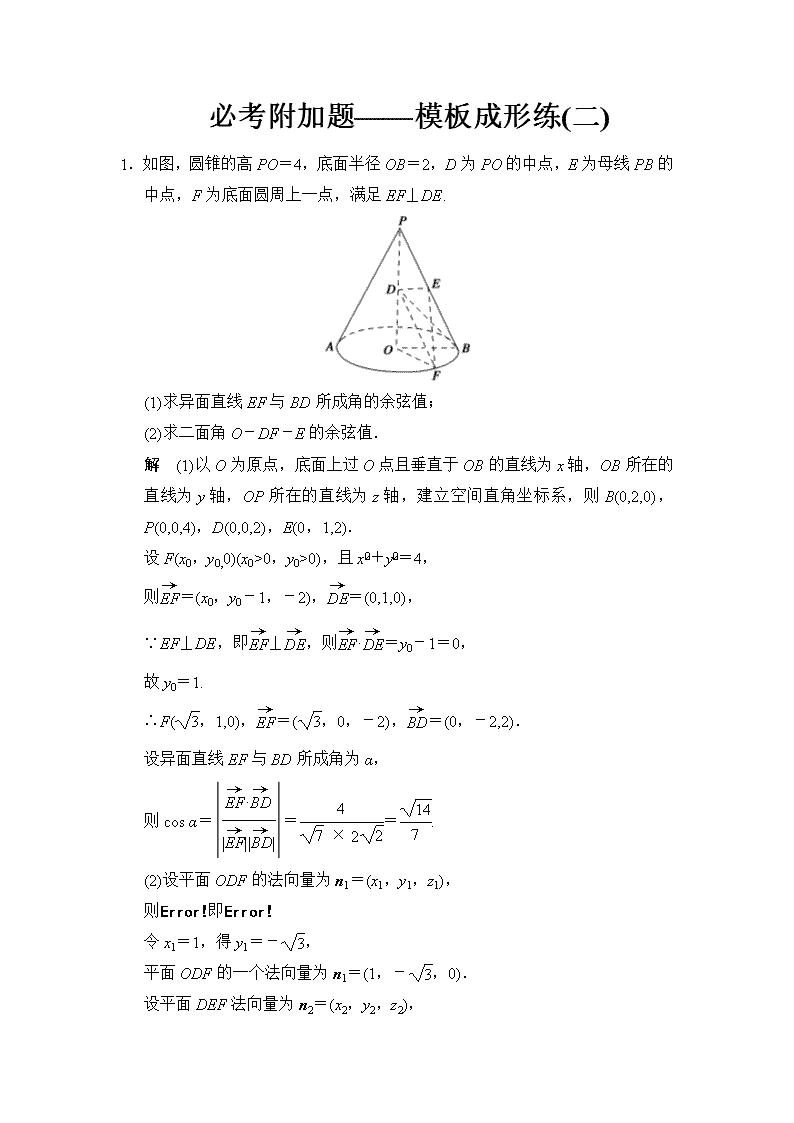
必考附加题——模板成形练(二)‎ ‎1．如图，圆锥的高PO＝4，底面半径OB＝2，D为PO的中点，E为母线PB的中点，F为底面圆周上一点，满足EF⊥DE.‎ ‎(1)求异面直线EF与BD所成角的余弦值；‎ ‎(2)求二面角O－DF－E的余弦值．‎ 解　(1)以O为原点，底面上过O点且垂直于OB的直线为x轴，OB所在的直线为y轴，OP所在的直线为z轴，建立空间直角坐标系，则B(0,2,0)，P(0,0,4)，D(0,0,2)，E(0，1,2)．‎ 设F(x0，y0,0)(x0>0，y0>0)，且x＋y＝4，‎ 则＝(x0，y0－1，－2)，＝(0,1,0)，‎ ‎∵EF⊥DE，即⊥，则·＝y0－1＝0，‎ 故y0＝1.‎ ‎∴F(，1,0)，＝(，0，－2)，＝(0，－2,2)．‎ 设异面直线EF与BD所成角为α，‎ 则cos α＝＝＝.‎ ‎(2)设平面ODF的法向量为n1＝(x1，y1，z1)，‎ 则即 令x1＝1，得y1＝－，‎ 平面ODF的一个法向量为n1＝(1，－，0)．‎ 设平面DEF法向量为n2＝(x2，y2，z2)，‎ 同理可得平面DEF的一个法向量为n2＝.‎ 设二面角O－DF－E的平面角为β，‎ 则|cos β|＝＝＝，‎ ‎∴sin β＝.‎ ‎2．已知数列{an}满足a1＝2，an＋1＝a－(n＋1)．‎ ‎(1)证明：an>n(n≥3)；‎ ‎(2)证明：<2.‎ 证明　(1)因为a1＝2，a2＝2，所以a3＝a－3＝5>3.‎ 假设当n＝k时，ak>k(k≥3)，‎ 则a>kk＋1>k2·k≥9k>2k＋2，‎ 那么，当n＝k＋1时，有 ak＋1＝a－(k＋1)>2k＋2－(k＋1)＝k＋1.‎ 这就是说，当n＝k＋1时，结论也成立．‎ 所以当n≥3时，an>n.‎ ‎(2)当n＝2时，<2显然成立，‎ 由(1)知，当n≥3时，an＝a－n>0，得a>n，‎ 所以an－1>，所以a－(n－1)>，‎ 即a>(n－1)＋，‎ 所以an－2>，以此类推，‎ 得2＝a1> ，问题得证．‎ ‎3．如图，在棱长为2的正方体ABCD－A1B1C1D1中，E，F分别为AD，DC的中点．‎ ‎(1)求直线BC1与平面EFD1所成角的正弦值；‎ ‎(2)设直线BC1上一点P满足平面PAC∥平面EFD1，求PB的长．‎ 解　(1)建立以D点为原点，DA所在直线为x轴，DC所在直线为y轴，DD1所在直线为z轴的空间直角坐标系．‎ D1(0,0,2)，A(2,0,0)，B(2,2,0)，‎ E(1,0,0)，C1(0,2,2)，F(0,1,0)，‎ ＝(－2,0,2)，＝(1,0，－2)，＝(－1,1,0)．‎ 设平面D1EF的法向量为n＝(x1，y1，z1)，‎ 则⇒ 令x1＝2，则n＝(2,2,1)，‎ cos〈n，〉＝＝－，‎ ‎∴直线BC1与平面EFD1所成角的正弦值为.‎ ‎(2)＝λ＝(－2λ，0,2λ)，‎ ＝＋＝(－2λ，2,2λ)，‎ n·＝－4λ＋4＋2λ＝0，∴λ＝2.‎ ‎∵AP不在平面EFD1内，AP∥平面EFD1，‎ 又AC∥EF，EF⊆平面EFD1，‎ ‎∴AC∥平面EFD1.‎ 又AP与AC相交于点A，‎ ‎∴平面PAC∥平面EFD1，‎ ＝(－4,0,4)，||＝4.‎ ‎4．已知数集A＝{a1，a2，…，an}，其中0≤a1a8，‎ 故a8＋a8∉A，∴0＝a8－a8∈A，故a1＝0.‎ ‎∵0＝a1a8，‎ 故a8＋ak∉A(k＝2,3，…，8)．‎ 由A具有性质P知，a8－ak∈A(k＝2,3，…，8)，‎ 又∵a8－a8