2020版高考数学二轮复习 专题六 统计与概率 专题对点练21 6 6页

专题对点练21　6.1~6.2组合练 ‎(限时90分钟,满分100分)‎ 一、选择题(共9小题,满分45分)‎ ‎1.某高校共有学生3 000人,新进大一学生有800人.现对大学生社团活动情况进行抽样调查,用分层抽样方法在全校抽取300人,则应在大一抽取的人数为(　　)‎ A.200 B.100 ‎ C.80 D.75‎ ‎2.‎ 如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为(　　)‎ A.3,5 B.5,5 ‎ C.3,7 D.5,7‎ ‎3.已知在数轴上0和3之间任取一个实数x,则使“log2x<‎1”‎的概率为(　　)‎ A. B. C. D.‎ ‎4.为考察某种药物对预防禽流感的效果,在四个不同的实验室取相同的个体进行动物试验,根据四个实验室得到的列联表画出如下四个等高条形图,最能体现该药物对预防禽流感有效果的图形是(　　)‎ ‎5.在区间[-3,3]内随机取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为(　　)‎ A. B. C. D.‎ ‎6.现采用随机模拟的方法估计某运动员射击4次至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1,2表示没有击中目标,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:‎ ‎7527　0293　7140　9857　0347　4373　8636　6947　1417　4698　0371　6233　2616　8045　6011　3661　9597　7424　7610　4281‎ 根据以上数据估计该射击运动员射击4次至少击中3次的概率为(　　)‎ A.0.55 ‎B.0.6 ‎ C.0.65 D.0.7‎ ‎7.设样本数据x1,x2,…,x10的平均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的平均值和方差分别为(　　)‎ A.1+a,4 B.1+a,4+a ‎ 6‎ C.1,4 D.1,4+a ‎8.(2018广东深圳调研)某食品研究部门为了解一种酒品的储藏年份与芳香度之间的相关关系,在市场上收集到了一部分不同年份的该酒品,并测定了其芳香度(如下表):‎ 年份x ‎0‎ ‎1‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 芳香度y ‎1.3‎ ‎1.8‎ ‎5.6‎ ‎7.4‎ ‎9.3‎ 由最小二乘法得到回归方程=1.03x+1.13,但不小心在检测后滴到表格上一滴检测液,污损了一个数据,请你推断该数据为(　　)‎ A.6.1 ‎B.‎6.28 ‎C.6.5 D.6.8‎ ‎9.已知半径为r的圆内切于某等边三角形,若在该三角形内任取一点,则该点到圆心的距离大于半径r的概率为(　　)‎ A. B.1- C. D.1-‎ 二、填空题(共3小题,满分15分)‎ ‎10.(2018江苏,3)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为　　　　　. ‎ ‎11.(2018上海,9)有编号互不相同的五个砝码,其中‎5克、‎3克、‎1克砝码各一个,‎2克砝码两个,从中随机选取三个,则这三个砝码的总质量为‎9克的概率是　　　　　.(结果用最简分数表示) ‎ ‎12.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请200名同学每人随机写下一个都小于1的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计π的值.假如统计结果是m=56,那么可以估计π≈　　　　.(用分数表示) ‎ 三、解答题(共3个题,满分分别为13分,13分,14分)‎ ‎13.如图所示,茎叶图记录了甲、乙两组5名工人制造某种零件的个数.‎ ‎(1)求甲组工人制造零件的平均数和方差;‎ ‎(2)分别从甲、乙两组中随机选取一名工人,求这两名工人制造的零件总数不超过20的概率.‎ 6‎ ‎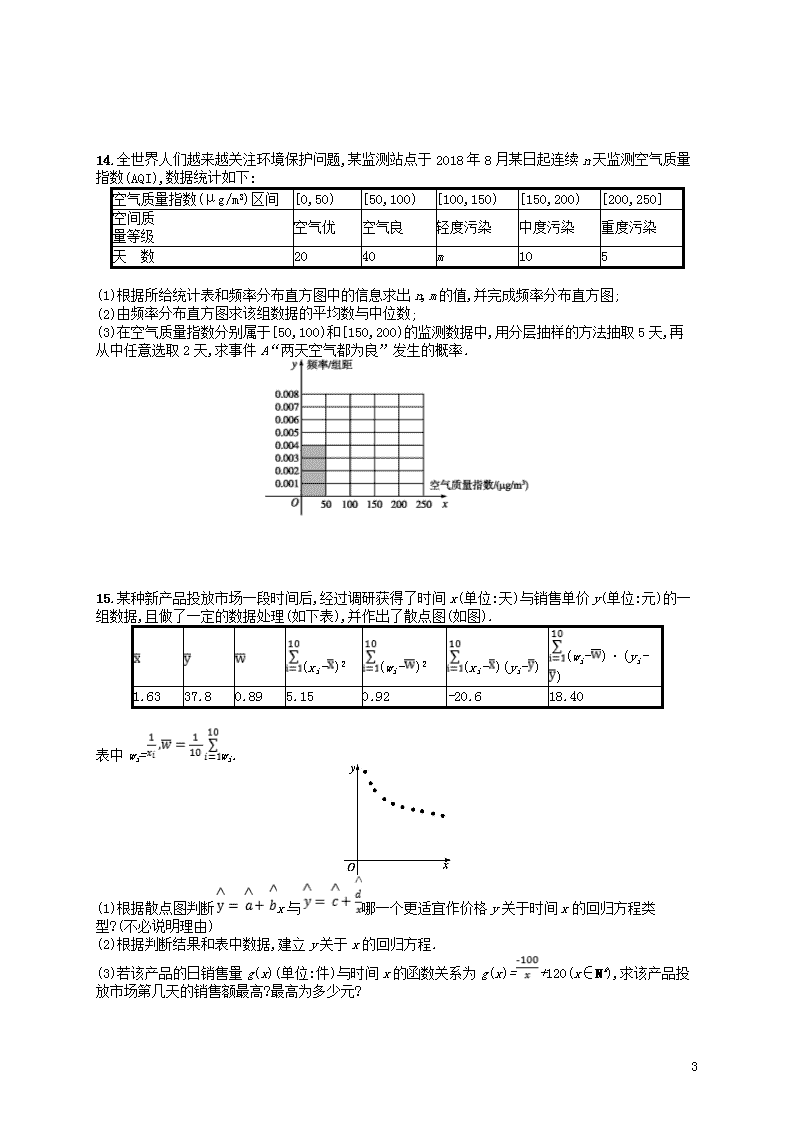14.全世界人们越来越关注环境保护问题,某监测站点于2018年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:‎ 空气质量指数(μg/m3)区间 ‎[0,50)‎ ‎[50,100)‎ ‎[100,150)‎ ‎[150,200)‎ ‎[200,250]‎ 空间质 量等级 空气优 空气良 轻度污染 中度污染 重度污染 天　数 ‎20‎ ‎40‎ m ‎10‎ ‎5‎ ‎(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;‎ ‎(2)由频率分布直方图求该组数据的平均数与中位数;‎ ‎(3)在空气质量指数分别属于[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件A“两天空气都为良”发生的概率.‎ ‎15.某种新产品投放市场一段时间后,经过调研获得了时间x(单位:天)与销售单价y(单位:元)的一组数据,且做了一定的数据处理(如下表),并作出了散点图(如图).‎ ‎(xi-)2‎ ‎(wi-‎)2‎ ‎(xi-)(yi-)‎ ‎(wi-‎)·(yi-)‎ ‎1.63‎ ‎37.8‎ ‎0.89‎ ‎5.15‎ ‎0.92‎ ‎-20.6‎ ‎18.40‎ 表中wi=wi.‎ ‎(1)根据散点图判断x与哪一个更适宜作价格y关于时间x的回归方程类型?(不必说明理由)‎ ‎(2)根据判断结果和表中数据,建立y关于x的回归方程.‎ ‎(3)若该产品的日销售量g(x)(单位:件)与时间x的函数关系为g(x)=+120(x∈N*),求该产品投放市场第几天的销售额最高?最高为多少元?‎ 6‎ 附:对于一组数据(u1,v1),(u2,v2),(u3,v3),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为.‎ 6‎ 专题对点练21答案 ‎1.C　解析 设大一抽取的人数为x,则用分层抽样的方法可得,解得x=80.故选C.‎ ‎2.A　解析 甲组数据为56,62,65,70+x,74;乙组数据为59,61,67,60+y,78.若两组数据的中位数相等,则65=60+y,所以y=5.‎ 又两组数据的平均值相等,所以56+62+65+70+x+74=59+61+67+65+78,解得x=3.‎ ‎3.C　解析 由log2x<1,得00},得2+a-a2>0,‎ 解得-10}这个事件的测度为3,‎ 故区间[-3,3]内随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为,故选D.‎ ‎6.B　解析 由题意知模拟射击4次的结果,经随机模拟产生了20组随机数,‎ 在20组随机数中表示射击4次至少击中3次的有:7527,9857,0347,4373,8636,6947,4698,6233,8045,3661,9597,7424,共12组随机数,‎ 故所求概率P≈=0.6.故选B.‎ ‎7.A　解析 由题意知yi=xi+a(i=1,2,…,10),则(x1+x2+…+x10+‎10a)=(x1+x2+…+x10)+a=+a=1+a,‎ 方差s2=[(x1+a--a)2+(x2+a--a)2+…+(x10+a--a)2]=[(x1-)2+(x2-)2+…+(x10-)2]=s2=4.故选A.‎ ‎8.A　解析 =4,因为样本中心点在回归直线=1.03x+1.13上,所以将x=4代入回归方程=1.03x+1.13,可得=5.25.设该数据的值为m,由5.25=,解得m=6.1,‎ 即该数据为6.1.故选A.‎ ‎9.B　解析 已知半径为r的圆内切于某等边三角形,则等边三角形的边长为2r,‎ 故该点到圆心的距离大于半径r的概率为1-=1-.‎ ‎10.90　解析 由题中茎叶图可知,5位裁判打出的分数分别为89,89,90,91,91,故平均数为=90.‎ ‎11.　解析 从编号互不相同的五个砝码中随机选取三个,总的结果数为10,其中选取的三个砝码的总质量为‎9克的有两种,所以所求概率为.‎ ‎12.　解析 由题意,得200对都小于1的正实数对(x,y),对应区域的面积为1,‎ 两个数能与1构成钝角三角形三边的数对(x,y),满足x2+y2<1且x,y都小于1,x+y>1,面积为.‎ 因为统计两数能与1构成钝角三角形三边的数对(x,y)的个数m=56,‎ 所以,所以π≈.故答案为.‎ ‎13.解 (1)甲组工人制造零件数为9,9,10,10,12,故甲组工人制造零件的平均数 (9+9+10+10+12)=10,‎ 方差为s2= [(9-10)2+(9-10)2+(10-10)2+(10-10)2+(12-10)2]=.‎ ‎(2)由题意,得甲、乙两组工人制造零件的个数分别是:‎ 甲:9,9,10,10,12;乙:8,9,9,10,11,‎ 甲组中5名工人分别记为a,b,c,d,e,乙组中5名工人分别记为A,B,C,D,E,‎ 分别从甲、乙两组中随机选取1名工人,共有25种方法,‎ 6‎ 制造零件总数超过20的有:‎ eB,eC,eD,eE,dE,cE,共6种,‎ 故这两名工人制造的零件总数不超过20的概率P=1-.‎ ‎14.解 (1)0.004×50=,解得n=100.‎ ‎20+40+m+10+5=100,解得m=25,=0.008,=0.005,=0.002,=0.001.‎ 完成频率分布直方图如下图:‎ ‎(2)由频率分布直方图知该组数据的平均数为 ‎=25×0.004×50+75×0.008×50+125×0.005×50+175×0.002×50+225×0.001×50=95.‎ ‎∵[0,50)的频率为0.004×50=0.2,[50,100)的频率为0.008×50=0.4,‎ ‎∴该组数据的中位数为50+×50=87.5.‎ ‎(3)在空气质量指数为[50,100)和[150,200)的监测天数中分布抽取4天和1天,在所抽取的5天中,将空气质量指数为[50,100)的4天分别记为a,b,c,d,将空气质量指数为[150,200)的1天记为e.‎ 从中任取2天的基本事件分别为:(a,b),(a,c),(a,d),(a,e),(b, c),(b,d),(b,e),(c,d),(c,e),(d,e),共10个,‎ 其中事件A“两天空气都为良”包含的基本事件为:‎ ‎(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),共6个,‎ ‎∴事件A“两天空气都为良”发生的概率P(A)=.‎ ‎15.解 (1)由散点图可以判断适合作价格y关于时间x的回归方程类型.‎ ‎(2)令w=,先建立y关于w的线性回归方程.∵=20,‎ ‎∴=37.8-20×0.89=20,‎ ‎∴y关于w的线性方程为=20+20w,‎ ‎∴y关于x的线性方程为=20+.‎ ‎(3)日销售额h(x)=g(x)‎ ‎=-200‎ ‎=-2 000,‎ 故x=10时,h(x)有最大值2 420元,‎ 即该产品投放市场第10天的销售额最高,最高为2 420元. ‎ 6‎