闵行区高考数学一模试卷含答案 9页

‎ 2017年闵行区高考数学一模试卷含答案 ‎ （满分150分，时间120分钟）‎ 考生注意：‎ ‎1．答卷前，考生务必在答题纸上将学校、班级、考生号、姓名等填写清楚．‎ ‎2．请按照题号在答题纸各题答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ ‎3．本试卷共有21道试题．‎ 一、填空题（本大题共有12题，满分54分）考生应在答题纸上相应编号的空格内直接填写结果，第1～6题每个空格填对得4分，第7～12题每个空格填对得5分，否则一律得零分．‎ 1. 方程的解_____________． ‎ 2. 若关于x的不等式的解集为，则____． ‎ 3. 已知数列的前项和为，则此数列的通项公式为___________． ‎ 4. 函数的反函数是_____________． ‎ C1‎ D1‎ B1‎ A1‎ C A B D M E 5. 的展开式中项的系数为___________．（用数字作答）‎ 6. 如右图，已知正方体，，为棱的中点，则三棱锥的体积为________________． ‎ 7. 从单词“”中任意选取4个不同的字母排成一排，则其中含 有“”的共有_____________种排法．（用数字作答） ‎ 8. 集合 _____．（用列举法表示）‎ 9. 如右图，已知半径为的扇形，，为弧上的一个动点，则的取值范围是__________． ‎ 10. 已知满足曲线方程，则的取值范围是____________． ‎ 11. 已知两个不相等的非零向量和，向量组和均由个和 个排列而成.记，那么的所有可能取值中的最小值是________________．（用向量表示）‎ 1. 已知无穷数列，，对任意，有，数列满足（），若数列中的任意一项都在该数列中重复出现无数次，则满足要求的的值为_______________． ‎ 二、选择题（本大题共有4题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．‎ 2. 若为实数，则“”是“”的 ( )‎ ‎(A) 充要条件 (B) 充分不必要条件 ‎(C) 必要不充分条件 (D) 既不充分也不必要条件 3. 若为实数，（是虚数单位），则 ( )‎ ‎(A) (B) (C) (D) ‎ 4. 函数在区间上的最大值是，那么实数的取值范围是 ( )‎ ‎(A) (B) (C) (D) ‎ 5. 曲线:，曲线:，它们交点的个数 ( )‎ ‎ (A) 恒为偶数 (B) 恒为奇数 (C) 不超过 (D) 可超过 三、解答题（本大题满分76分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．‎ 6. ‎（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．‎ A B O D C 如图，在中，，斜边，是的中点．现将以直角边为轴旋转一周得到一个圆锥，点为圆锥底面圆周上的一点，且， 求：‎ ‎（1）圆锥的侧面积；‎ ‎（2）直线与平面所成的角的大小．（用反三角函数表示）‎ 7. 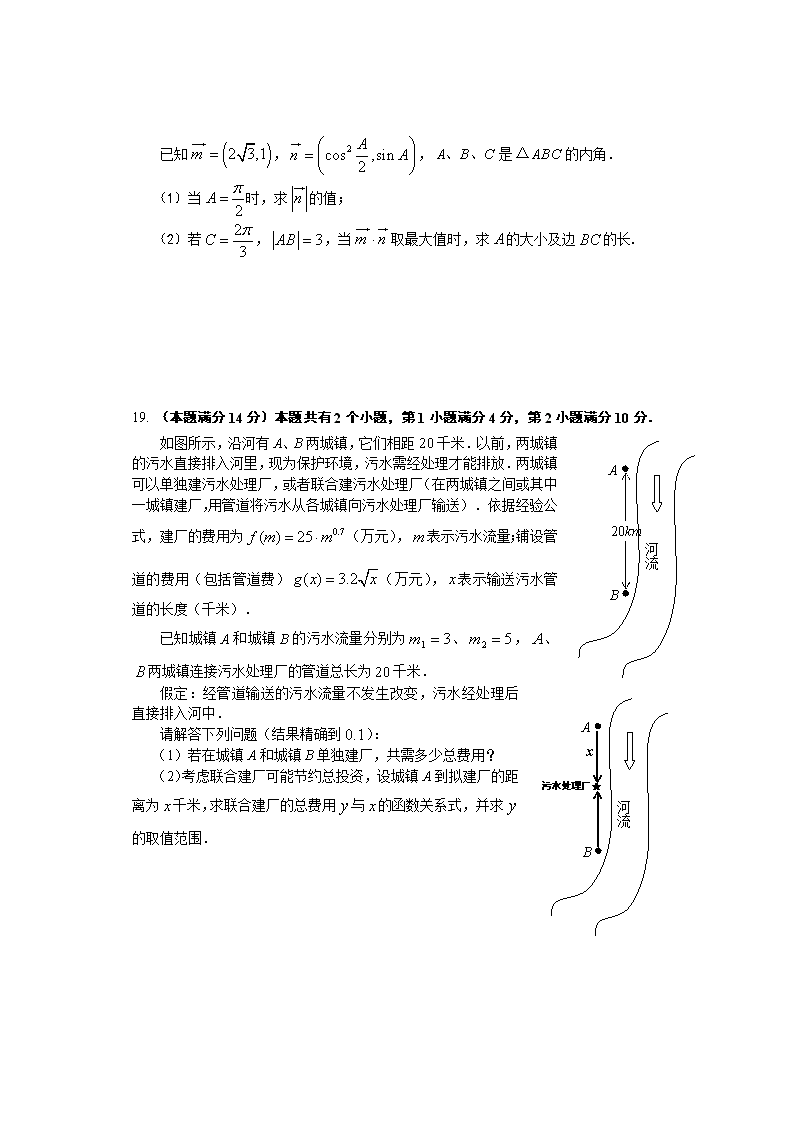‎（本题满分14分）本题共有2个小题，第1小题满分4分，第2小题满分10分．‎ 已知，，是的内角．‎ ‎（1）当时，求的值；‎ ‎（2）若，，当取最大值时，求的大小及边的长.‎ 1. ‎（本题满分14分）本题共有2个小题，第1小题满分4分，第2小题满分10分． ‎ 河流 A B ‎20km 如图所示，沿河有A、B两城镇，它们相距千米．以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放．两城镇可以单独建污水处理厂，或者联合建污水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送）．依据经验公式，建厂的费用为（万元），表示污水流量；铺设管道的费用（包括管道费）（万元），表示输送污水管道的长度（千米）．‎ 已知城镇A和城镇B的污水流量分别为、，、两城镇连接污水处理厂的管道总长为千米．‎ 河流 A B 污水处理厂★‎ x 假定：经管道输送的污水流量不发生改变，污水经处理后直接排入河中．‎ 请解答下列问题（结果精确到）：‎ ‎（1）若在城镇A和城镇B单独建厂，共需多少总费用？‎ ‎（2）考虑联合建厂可能节约总投资，设城镇A到拟建厂的距离为千米，求联合建厂的总费用与的函数关系式，并求的取值范围．‎ 1. ‎(本题满分16分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分．‎ ‎ 如图，椭圆的左、右顶点分别为、，双曲线以、为顶点，焦距为．点是上在第一象限内的动点，直线与椭圆相交于另一点，线段的中点为，记直线的斜率为，为坐标原点．‎ ‎（1）求双曲线的方程；‎ ‎（2）求点的纵坐标的取值范围；‎ ‎（3）是否存在定直线，使得直线与直线关于直线对称？若存在，求直线的方程；若不存在，请说明理由．‎ 2. ‎ (本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分． ‎ 在平面直角坐标系上，有一点列，设点的坐标（），其中． 记，，且满足（）． ‎ ‎（1）已知点，点满足，求的坐标；‎ ‎（2）已知点，（），且（）是递增数列，点在直线：上，求；‎ ‎（3）若点的坐标为，，求的最大值．‎ ‎ ‎ 闵行区2016学年第一学期高三年级质量调研考试 数学试卷参考答案与评分标准 一. 填空题 1．； 2．； 3．； 4．； 5．160； 6．； 7．；8．；9．； 10．； 11．；12．2； ‎ A B O D C E 二. 选择题 13．C； 14．B； 15．C； 16．D．‎ 三. 解答题 ‎ ‎17．[解] （1） …………………………2分 ‎ …………………………6分 ‎（2）取的中点，连接、， ………………8分 则，所以，‎ 所以是直线与平面所成的角， …………10分 在中，， …………12分 所以 所以直线与平面所成的角的大小为（）…………14分 ‎18．[解] （1）当时， …………4分 ‎（2） …………6分 ‎ ‎ …………………………8分 取到最大值时 ， …………………………10分 由正弦定理， …………………………12分 ‎ 解得 …………………………14分 ‎19．[解] （1）分别单独建厂，共需总费用 万元 …………………………4分 ‎（2）联合建厂，共需总费用 ‎（）‎ 所以与的函数关系式为（）……8分 令（）‎ ‎ ………10分 的取值范围为． …………………………14分 ‎20．[解] ‎ ‎（1）设双曲线的方程为，双曲线的焦距为；………2分 依题意可得， ，‎ ‎；‎ ‎ ‎ 双曲线的方程为 …………………………4分 ‎ (2) 由题意可知，直线的斜率皆存在，且不为零．‎ 设点、，‎ 直线的方程为 （）‎ 联立方程组 整理，得， ………6分 解得，或，，‎ 得，， ………8分 ‎ 因为， 在上是增函数，所以………10分 ‎（或者，当且仅当时取等号，所以）（3）方法一：由题（2）知直线的方程为: ………………12分 同理，解方程组，可得，‎ 得点的坐标为 ‎ 直线的斜率 直线的方程为:， …………………………14分 联立直线与直线的方程，解得，‎ 因为直线与的斜率互为相反数，所以直线与关于直线对称． …………………………16分 方法二：由在双曲线上可得： ‎ 所以 …………………………12分 同理，即, …………………………14分 因此 设直线:，则直线:,解得 因为直线与的斜率互为相反数，所以直线与关于直线对称． …………………………16分 ‎21．[解] （1）因为、，所以 又因为，， 所以 ………………2分 所以，‎ 所以点的坐标为 …………………………4分 ‎（2）因为，（），‎ 得 ………………………6分 又，，得（），‎ 因为，而（）是递增数列，‎ 故（）‎ ‎， ……………………8分 所以 ‎ 将代入，得，得 ……………10分 ‎（3）‎ ‎ …………………………12分 记 ‎ …………………………14分 因为是偶数，，‎ ‎…16分 当，‎ 时（取法不唯一），‎ 所以 …………………………18分