高中物理必修二知识点总结及典型题解析 20页

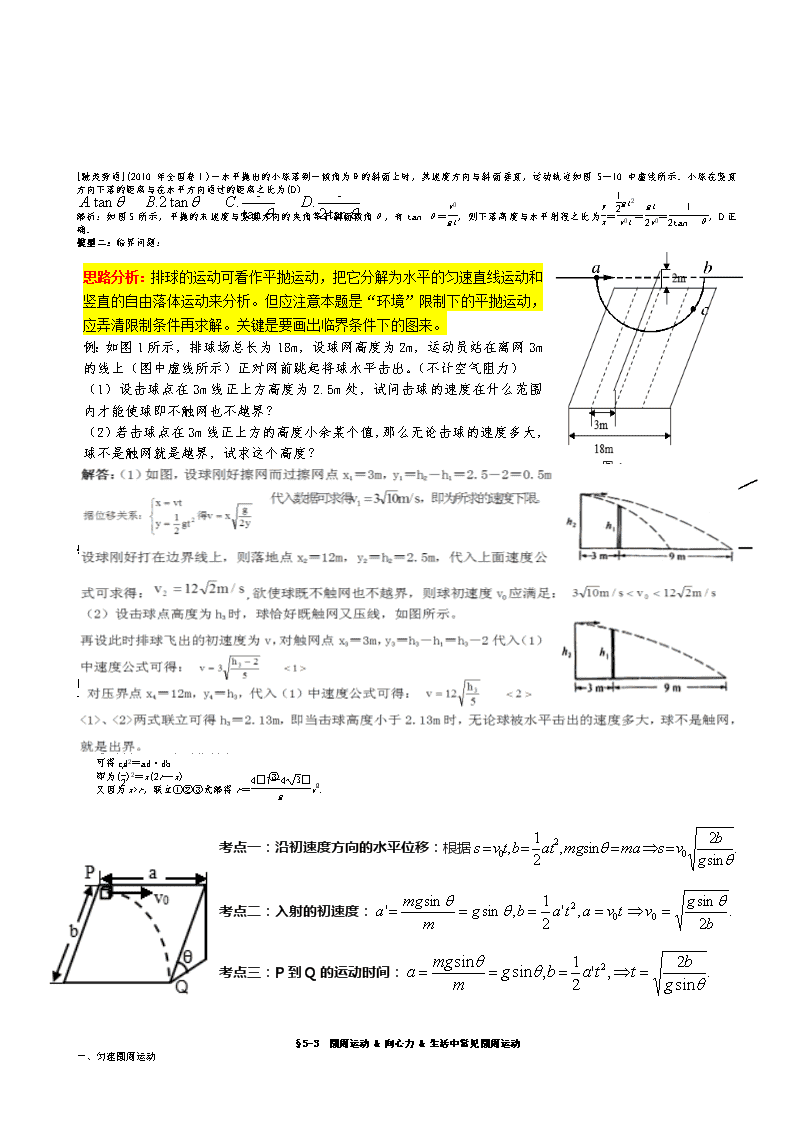
第五章平抛运动§5-1曲线运动&运动的合成与分解一、曲线运动1.定义：物体运动轨迹是曲线的运动。2.条件：运动物体所受合力的方向跟它的速度方向不在同一直线上。3.特点：①方向：某点瞬时速度方向就是通过这一点的曲线的切线方向。②运动类型：变速运动（速度方向不断变化）。③F合≠0，一定有加速度a。④F合方向一定指向曲线凹侧。⑤F合可以分解成水平和竖直的两个力。4.运动描述——蜡块运动P蜡块的位置vvxvy涉及的公式：θ二、运动的合成与分解1.合运动与分运动的关系：等时性、独立性、等效性、矢量性。2.互成角度的两个分运动的合运动的判断：①两个匀速直线运动的合运动仍然是匀速直线运动。②速度方向不在同一直线上的两个分运动，一个是匀速直线运动，一个是匀变速直线运动，其合运动是匀变速曲线运动，a合为分运动的加速度。③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。④两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时，合运动是匀变速直线运动，否则即为曲线运动。三、有关“曲线运动”的两大题型（一）小船过河问题模型一：过河时间t最短：模型二：直接位移x最短：模型三：间接位移x最短：dvv水v船θ当v水v船时，，，θv船dvv水v船θ，d[触类旁通]1．(2011年上海卷)如图5－4所示，人沿平直的河岸以速度v行走，且通过不可伸长的绳拖船，船沿绳的方向行进．此过程中绳始终与水面平行，当绳与河岸的夹角为α时，船的速率为（C）。解析：依题意，船沿着绳子的方向前进，即船的速度总是沿着绳子的，根据绳子两端连接的物体在绳子方向上的投影速度相同，可知人的速度v在绳子方向上的分量等于船速，故v船＝vcosα，C正确．2．(2011年江苏卷)如图5－5所示，甲、乙两同学从河中O点出发，分别沿直线游到A点和B点后，立即沿原路线返回到O点，OA、OB分别与水流方向平行和垂直，且OA＝OB.若水流速度不变，两人在静水中游速相等，则他们所用时间t甲、t乙的大小关系为(C)A．t甲t乙D．无法确定解析：设游速为v，水速为v0，OA＝OB＝l，则t甲＝＋；乙沿OB运动，乙的速度矢量图如图4所示，合速度必须沿OB方向，则t乙＝2·，联立解得t甲>t乙，C正确．（二）绳杆问题(连带运动问题)1、实质：合运动的识别与合运动的分解。2、关键：①物体的实际运动是合速度，分速度的方向要按实际运动效果确定；②沿绳（或杆）方向的分速度大小相等。模型四：如图甲，绳子一头连着物体B，一头拉小船A，这时船的运动方向不沿绳子。BOOAvAθv1v2vA甲乙 处理方法：如图乙，把小船的速度vA沿绳方向和垂直于绳的方向分解为v1和v2，v1就是拉绳的速度，vA就是小船的实际速度。[触类旁通]如图，在水平地面上做匀速直线运动的汽车，通过定滑轮用绳子吊起一个物体，若汽车和被吊物体在同一时刻的速度分别为v1和v2，则下列说法正确的是(C）A．物体做匀速运动，且v2＝v1B．物体做加速运动，且v2>v1C．物体做加速运动，且v2r，联立①②③式解得r＝v.考点一：沿初速度方向的水平位移：根据考点二：入射的初速度：考点三：P到Q的运动时间：§5-3圆周运动&向心力&生活中常见圆周运动 一、匀速圆周运动1.定义：物体的运动轨迹是圆的运动叫做圆周运动，物体运动的线速度大小不变的圆周运动即为匀速圆周运动。2.特点：①轨迹是圆；②线速度、加速度均大小不变，方向不断改变，故属于加速度改变的变速曲线运动，匀速圆周运动的角速度恒定；③匀速圆周运动发生条件是质点受到大小不变、方向始终与速度方向垂直的合外力；④匀速圆周运动的运动状态周而复始地出现，匀速圆周运动具有周期性。3.描述圆周运动的物理量：（1）线速度v是描述质点沿圆周运动快慢的物理量，是矢量；其方向沿轨迹切线，国际单位制中单位符号是m/s，匀速圆周运动中，v的大小不变，方向却一直在变；（2）角速度ω是描述质点绕圆心转动快慢的物理量，是矢量；国际单位符号是rad／s；（3）周期T是质点沿圆周运动一周所用时间，在国际单位制中单位符号是s；（4）频率f是质点在单位时间内完成一个完整圆周运动的次数，在国际单位制中单位符号是Hz；（5）转速n是质点在单位时间内转过的圈数，单位符号为r/s，以及r/min．4.各运动参量之间的转换关系：5.三种常见的转动装置及其特点：ABr2r1rROBA模型一：共轴传动模型二:皮带传动模型三：齿轮传动ABOrRO[触类旁通]1、一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定，有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动，如图所示，A的运动半径较大，则(AC)A．A球的角速度必小于B球的角速度B．A球的线速度必小于B球的线速度C．A球的运动周期必大于B球的运动周期D．A球对筒壁的压力必大于B球对筒壁的压力解析：小球A、B的运动状态即运动条件均相同，属于三种模型中的皮带传送。则可以知道，两个小球的线速度v相同，B错；因为RA>RB，则ωA<ωB,TA小球固定在轻杆的一端在竖直平面内转动杆对球可以是拉力也可以是支持力①若F＝0，则mg＝，v＝②若F向下，则mg＋F＝m，v>③若F向上，则mg－F＝或mg－F＝0，则0≤v<小球在竖直细管内转动管对球的弹力FN可以向上也可以向下依据mg＝判断，若v＝v0，FN＝0；若vv0，FN向下球壳外的小球在最高点时弹力FN的方向向上①如果刚好能通过球壳的最高点A，则vA＝0，FN＝mg②如果到达某点后离开球壳面，该点处小球受到壳面的弹力FN＝0，之后改做斜抛运动，若在最高点离开则为平抛运动六、有关生活中常见圆周运动的涉及的几大题型分析（一）解题步骤：①明确研究对象；②定圆心找半径；③对研究对象进行受力分析；④对外力进行正交分解；⑤列方程：将与和物体在同一圆周运动平面上的力或其分力代数运算后，另得数等于向心力；⑥解方程并对结果进行必要的讨论。（二）典型模型：I、圆周运动中的动力学问题谈一谈：圆周运动问题属于一般的动力学问题，无非是由物体的受力情况确定物体的运动情况，或者由物体的运动情况求解物体的受力情况。解题思路就是，以加速度为纽带，运用那个牛顿第二定律和运动学公式列方程，求解并讨论。a、涉及公式：①②，由①②得：。b、分析：设转弯时火车的行驶速度为v，则：（1）若v>v0，外轨道对火车轮缘有挤压作用；（2）若vv3、ω1>ω3，A错B对．Q点是圆周轨道1与椭圆轨道2的相切点，由于万有引力提供向心力，则有G＝ma向，所以a向＝，显然，卫星在经过圆周轨道1上的Q点和在经过椭圆轨道2上的Q点时具有的向心加速度均为a向＝，C错；同理可得D对．3、(多选)地球同步卫星到地心的距离r可由r3＝求出．已知式中x的单位是m,y的单位是s，z的单位是m/s2，则A．x是地球半径，y是地球自转的周期，z是地球表面处的重力加速度B．x是地球半径，y是同步卫星绕地心运动的周期，z是同步卫星的加速度C．x是赤道周长，y是地球自转周期，z是同步卫星的加速度D．x是地球半径，y是同步卫星绕地心运动的周期，z是地球表面处的重力加速度解析：由，可得r3＝①，与题目中给出的r3＝相比需再作进一步处理．考虑到z的单位是m/s2，是加速度的单位，于是引入加速度a＝G②，上式中a为同步卫星的加速度，r为同步卫星到地心的距离，由①②两式可得r3＝，显然与所有选项不对应；引入地球表面处的重力加速度：g＝G③，由①③两式可得r3＝，与r3＝相比，形式相同，并且与A、D对应．对于同步卫星，其绕地心运动的周期与地球自转周期T相同．【题外延伸】此题不能靠单纯分析量纲来验证结论，各选项都符合量纲，无法求解．要结合同步卫星的知识进行推导，推导的方向是既要符合题目中给出的r3＝形式，又要符合选项的要求．在推导的过程中思路要清晰，量纲要相符，形式要相同，表面上看是一件很难的事情，其实只要尝试多几次即可．4、(多选)下列关于同步卫星的说法，正确的是(AC）。A．同步卫星和地球自转同步，卫星的高度和速率是确定的B．同步卫星的角速度是确定的，但高度和速率可以选择，高度增加，速率增大，且仍保持同步C．一颗人造地球卫星的周期是114min，比同步卫星的周期短，所以这颗人造地球卫星离地面的高度比同步卫星低D．同步卫星的速率比地球大气层附近的人造卫星的速率大解析：同步卫星和地球自转同步，即它们的周期T相同，同步卫星绕地心近似做匀速圆周运动，所需向心力由卫星m和地球M之间的万有引力提供．设地球半径为R，同步卫星高度为h，因为F引＝F向，所以G＝m(R＋h)，得h＝－R，可见h是一定的；由G＝m得：v＝，可见v也是一定的，A正确．由于同步卫星的周期确定，即角速度确定，则h和v均随之确定，不能改变，否则不能同步，B错误．由h＝－R可知，当T变小时，h变小，可见，人造卫星离地面的高度比同步卫星低，速率比同步卫星大，C正确，D错误。5、2007年10月24日18时，“嫦娥一号”卫星星箭成功分离，卫星进入绕地轨道。在绕地运行时，要经过三次近地变轨：12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④。11月5日11时，当卫星经过距月球表面高度为h的A点时，再一次实施变轨，进入12小时椭圆轨道⑤，后又经过两次变轨，最后进入周期为T的月球极月圆轨道⑦。如图所示。已知月球半径为R。(1)请回答：“嫦娥一号”在完成三次近地变轨时需要加速还是减速？(2)写出月球表面重力加速度的表达式。解析：(1)加速(2)设月球表面的重力加速度为g月，在月球表面有G＝mg月，卫星在极月圆轨道有，G＝m()2(R＋h)，解得g月＝。6、2009年5月，航天飞机在完成对哈勃空间望远镜的维修任务后，在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ，B为轨道Ⅱ上的一点，如图所示，关于航天飞机的运动，下列说法中正确的有(ABC)A．在轨道Ⅱ上经过A的速度小于经过B的速度B．在轨道Ⅱ上经过A的动能小于在轨道Ⅰ上经过A的动能C．在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期D．在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度解析：逐项判断A．根据开普勒定律，近地点的速度大于远地点的速度，A正确；B．由I轨道变到II轨道要减速，所以B正确；C．根据开普勒定律，=c，R2＜R1，所以T2＜T1。C正确；D．根据a=，应等于，D错误。7、我国发射的“嫦娥一号” 卫星经过多次加速、变轨后，最终成功进入环月工作轨道。如图所示，卫星既可以在离月球比较近的圆轨道a上运动，也可以在离月球比较远的圆轨道b上运动。下列说法正确的是(D)A．卫星在a上运行的线速度小于在b上运行的线速度B．卫星在a上运行的周期大于在b上运行的周期C．卫星在a上运行的角速度小于在b上运行的角速度D．卫星在a上运行时受到的万有引力大于在b上运行时的万有引力解析：根据万有引力提供向心力，推导出线速度、角速度和周期与轨道半径的关系式。第七章机械能守恒定律运动§7-1能量&功&功率百度文库-让每个人平等地提升自我一、能量的转化和守恒1.能量的物理意义：一个物体如果具备了对外做功的本领，我们就说这个物体具有能量。能量是状态量，是标量，与物体的某一状态相对应。能量的表现形式多种多样，如动能、势能等。2.能量守恒与转化定律：能量只能从一种形式转化成另一种形式，或从一个物体转移到另一个物体，但能的总量保持不变，这就是能量守恒和转化定律。3.寻找守恒量的方法：寻找守恒量必须讲究科学的方法：如观察此消彼长的物理量、研究其相互的关系、科学构思巧妙实验、精确地论证、推理和计算等。二、功1.概念：如果一个物体受到力的作用，并在力的方向上发生了一段位移，则这个力就对物体做了功。2.公式：W=Flcosθ[F为该力的大小，l为力发生的位移，θ为位移l与力F之间的夹角]。注：功仅与F、S、θ有关，与物体所受的其它外力、速度、加速度无关。3.单位：焦耳，简称“焦”，符号J。4.标量：但它有正功、负功。功的正负表示能量传递的方向，或表示动力做功还是阻力做功，即表示做过的效果。5.物理意义：功是能量转化的量度。功是一个过程所对应的量，因此功是过程量。6.合力的功：①总功等于各个力对物体做功的代数和：；②总功等于合外力所做的功：W总=F合lcosθ。7.判断力F做功的情况的方法：①利用公式W=Flcosθ来判断：当时，即力与位移成锐角，力做正功，功为正当时，即力与位移垂直，力不做功，功为零当时，即力与位移成钝角，力做负功，功为负②看物体间是否有能量的转化或转移：若有能量的转化或转移，则必定有力做功。此方法常用于两个相互联系的物体。三、功率1.概念：描述力对物体做功快慢的物理量。2.公式：（定义式），适用于任何情况，。3.单位：瓦特，简称“瓦”，符号W。4.标量：功率表示功的变化率，是一种频率，只有大小，没有方向。5.分类：额定功率：指发动机正常工作时最大输出功率，电器的铭牌上写的功率即为额定功率；实际功率：指发动机实际输出的功率即发动机产生牵引力的功率，P实≤P额。6.机械效率：输入功率：机器工作时，外界对机器做功的功率。输出功率：极其对外做功的功率。机械效率：7.机车的两种启动方式：启动方式恒定功率启动恒定加速度启动过程分析阶段一：阶段二：阶段一：,直到P=P额=F·vm’。阶段二：.阶段三：。运动规律做加速度逐渐减小的变加速直线运动（对应下图中的OA段）→以vm做匀速直线运动（对应下图中AB段）以加速度a做匀加速直线运动（对应下图中的OA段，）→做加速度减小的变加速直线运动（对应下图中的AB段）→以vm做匀速直线运动（对应下图中的BC段）v-t图像vvmABOt1tvvm’ABOt1tCvmt0注意：①不管哪种启动方式，机动车的功率均是指牵引力的功率，对启动过程的分析也都是用分段分析法。②P=Fv中的F仅是机动车的牵引力，而非机动车所受的合力，这一点是在解题时极易出现错误的地方。§7-2重力做功&重力势能&弹性势能一、重力做功1.特点：重力做的功由重力大小和重力方向上发生的位移（数值方向上的高度差）决定。2.公式：WG=mg·Δh。3.注意：重力做功与物体的运动路径无关，只决定于运动初始位置的高度差。二、重力势能1.定义：物体由于位于高处而具有的能量。 2.表达式：Ep=mgh[h为物体重心到参考平面的竖直高度]，单位J。3.影响因素：物体的质量m和所在的高度h。4.标量：正负不表示方向。重力势能为正，表示物体在参考面的上方；重力势能为负，表示物体在参考面的下方；重力势能为零，表示物体在参考面的上。5.重力势能的变化：ΔEp=Ep2-Ep1，即末状态与初状态的重力势能的差值。6.对Ep=mgh的理解：①其中h为物体重心的高度。②重力势能具有相对性，是相对于选取的参考平面而言的。选择不同的参考平面，确定出的物体高度不一样，重力势能也不同。③重力势能可正可负，在参考平面上方重力势能为正值，在参考平面下方重力势能为负值。重力势能是标量，其正负表示比参考平面高或低。注：a、在计算重力势能时，应该明确选取参考平面。b、选择哪个水平面作为参考平面，可视研究问题的方便而定，通常选择地面作为参考平面。7.系统性：重力势能属于地球和物体所组成的系统，通常说物体具有多少重力势能，只是一种简略的说法。8.重力做功与重力势能变化的关系：重力势能变化的过程也就是重力做功的过程，重力做正功，重力势能减少；重力做负功，重力势能增加，即满足WG=-ΔEp=Ep1-Ep2。三、弹性势能1.概念：发生弹性形变的物体的各部分之间，由于弹力的相互作用具有势的能。2.表达式：，单位为J。3.影响因素：弹簧的劲度系数k和弹簧形变量x。4.弹力做功与弹性势能的关系：。弹力做正功时，物体弹性势能减少；弹力做负功时，物体弹性势能增加，即。§7-3动能&动能定理一、动能1.概念：物体由于运动而具有的能量，称为动能。2.表达式：，单位为J。3.影响因素：只与物体某状态下的速度大小有关，与速度的方向无关。注：动能是相对量（因为速度是相对量）。参考系不同，速度就不同，所以动能也不同，一般来说都以地面为参考系。4.动能的变化：，即末状态动能与初状态动能之差。注意：ΔEK>0，表示物体的动能增加；ΔEK<0，表示物体的动能减少。5.说明：①动能具有相对性，与参考系的选取有关，一般以地面为参考系描述物体的动能。②动能是表征物体运动状态的物理量，与时刻、位置对应。③动能是一个标量，有大小、无方向，且恒为正值。二、动能定理1.内容：力在一个过程中对物体做的功，等于物体在这个过程中动能的变化。2.表达式：。3.意义：动能定理指出了外力对物体所做的总功与物体动能变化之间的关系。即外力对物体所做的总功，对应于物体动能的变化，变化的大小由做功的多少来量度。4.适用情况：①适用于受恒力作用的直线运动，也适用于变力作用的曲线运动；②不涉及加速度和时间的问题中，首选动能定律；③求解多个过程的问题；④变力做功。5.解题步骤：①明确研究对象，找出研究对象初末运动状态（对应的速度）及其对应的过程；②对研究对象进行受力分析；③弄清外力做功的大小和正负，计算时将正负号代入；④当研究对象运动由几个物理过程所组成，则可以采用整体法进行研究。§7-4机械能守恒定律&能量守恒定律一、机械能守恒定律1.内容：在只有重力或弹簧弹力做功的物体系统内，动能与势能可以相互转化，而总的机械能保持不变。2.条件：只有重力或弹簧弹力做功。3.用法：①，系统中初末状态机械能总和相等，且初末状态必须用同一零势能计算势能。②，系统重力势能减少（增加）多少，动能就增加（减少）多少。③，系统中A部分增加（减少）多少，B部分就减少（增加）多少。4.解题步骤：①确定研究对象，分析研究对象的物理过程；②进行受力分析；③分析各力做功的情况，明确守恒条件；④选择零势能面，确定初末状态的机械能（必须用同一零势能计算势能）；⑤根据机械能守恒定律列方程。5.判断机械能守恒的方法：①从做功角度判断：分析物体或物体系的受力情况，明确各力做功的情况，若只有重力或弹簧弹力对物体或物体系做功，则物体或物体系机械能守恒；②从能量转化的角度来判断：若物体系中只有动能和势能的相互转化，而无机械能与其他形式的能的转化，则物体系的机械能守恒。二、能量守恒定律1.内容：能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为另一种形式，或从一个物体转移到另一个物体，在转化或转移的过程中，能量的总量保持不变。2.表达式：。3.意义：动能定理指出了外力对物体所做的总功与物体动能变化之间的关系。即外力对物体所做的总功，对应于物体动能的变化，变化的大小由做功的多少来量度。4.解题思路：①转化：同一系统中，A增必定存在B减，且增减量相等；②转移：两个物体A、B，只要A的某种能量增加，B的某种能量一定减少，且增减量相等。5.解题步骤：①分清有哪几种形式的能在变化；②分别列出减少的能量ΔE减和增加的能量ΔE增的表达式或列出最初的能量E初和最终的能量E末的表达式；③根据列等式求解。 §7-5综合：各种力做功的计算&功能关系一、各种力做功的计算问题1.恒力做功：（1）运用公式W=Flcosθ：使用此式时需找对真正做功的力F和它发生的位移lcosθ。注意：用此式计算只能计算恒力做功。（2）多个恒力的做功求解：①用平行四边形定则求出合外力，再根据W=F合lcosθ计算功。注意θ应是合外力与位移l间的夹角。②分别求出各个外力做的功:W1=F1lcosθ1,W2=F2lcosθ2…再求出各个外力做功的代数和W总=W1+W2+…。2.变力做功（物理八种常见的分析方法）：（1）等值法：若某一变力做的功和某一恒力做的功相等，则可以通过计算该恒力做的功，求出该变力做的功。恒力做功用计算。（2）功率法：若功率恒定，可根据W=Pt求变力做的功。（3）动能定理法：根据W=ΔEK计算。（4）功能分析法：某种功与某种能对应，可根据相应能的变化求对应的力做的功。（5）平均力法：如果力的方向不变，力的大小随位移按线性规律变化，可用算术平均值（恒力）代替变力，公式为。（6）图像法：如果参与做功的力是变力，方向与位移方向始终一致而大小随时间变化，我们可作出该力随位移变化的图像。如图，那么曲线与横坐标轴所围的面积，即为变力做的功。（7）极限法（极端法）：将所求的物理量推向极大或极小推断出现的情况，此方法适用于选择题中。（8）微元法：将一个过程分解成无数段极小的过程，即整个过程是由小过程组合而成，先分析小过程，从而引向总过程讨论分析，从而得出结论。3.摩擦力做功：（1）做功特点：①摩擦力既可以对物体做正功，也可以对物体做负功。②在相互存在的静摩擦力的系统中，一对静摩擦力中，一个做正功，另一个做负功，且功的代数和为0。③静摩擦力对物体做功的过程，是机械能在相互接触的物体之间转移的过程，没有机械能转化为内能。（2）摩擦力做的功与产生内能的关系：①滑动摩擦力做的功为负值，在数值上等于滑动摩擦力与相对位移的乘积，即W滑=-fs相对。②滑动摩擦力做的功在数值上等于存在相互摩擦力的系统机械能的减少量，根据能量守恒定律可知，滑动摩擦力做的功在数值上等于系统内产生的内能，即W滑=-ΔE。二、功和能的关系1.能量的转化必须通过做功才能实现：做功的过程就是能量转化的过程，某种力做功往往与某一具体的能量变化相对应。2.功是能量转化的量度：①合外力做的功（所有外力做的功）动能变化量；②重力做的功重力势能变化量；③弹簧弹力做的功弹性势能变化量；④外力（除重力、弹簧弹力）做的功机械能变化量：⑤弹簧弹力、重力做的功不引起机械能的变化；⑥一对滑动摩擦力做的功内能变化量；⑦电场力做的功电视能变化试题链接1．(2010年湖南师大附中模拟)如右图所示，一质量为m的小球固定于轻质弹簧的一端，弹簧的另一端固定于O点处，将小球拉至A处，弹簧恰好无形变，由静止释放小球，它运动到O点正下方B点的速度为v，与A点的竖直高度差为h，则(　AD　)A．由A至B重力做功为mghB．由A至B重力势能减少mv2C．由A至B小球克服弹力做功为mghD．小球到达位置B时弹簧的弹性势能为。2．质量为m的物体，从距地面h高处由静止开始以加速度a＝g竖直下落到地面，在此过程中(　B　)A．物体的重力势能减少mghB．物体的动能增加mghC．物体的机械能减少mghD．物体的机械能保持不变【解析】　物体所受合力为F合＝ma＝mg，由动能定理得，动能的增加量ΔEk＝F合·h＝mgh.3．如右图所示，具有一定初速度的物块，沿倾角为30°的粗糙斜面向上运动的过程中，受一个恒定的沿斜面向上的拉力F作用，这时物块的加速度大小为4m/s2，方向沿斜面向下，那么，在物块向上运动的过程中，正确的说法是(　A　)A．物块的机械能一定增加B．物块的机械能一定减小C．物块的机械能可能不变D．物块的机械能可能增加也可能减小【解析】　机械能变化的原因是非重力、弹力做功，题中除重力外，有拉力F和摩擦力Ff做功，则机械能的变化决定于F与Ff做功大小关系．由mgsinα＋Ff－F＝ma，知F－Ff＝mgsin30°－ma＞0，即F＞Ff.故F做正功多于克服摩擦力做功，故机械能增大．4．(2010年济宁模拟)如右图所示，固定斜面倾角为θ，整个斜面分为AB、BC两段，AB＝2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放，恰好能滑动到C点而停下，那么θ、μ1、μ2间应满足的关系是(　B　)A．tanθ＝　　　　　　B．tanθ＝C．tanθ＝2μ1－μ2D．tanθ＝2μ2－μ1 【解析】　由动能定理得mg·AC·sinθ－μ1mgcosθ·AB－μ2mgcosθ·BC＝0，则有tanθ＝，B项正确．5．两辆汽车在同一平直路面上行驶，它们的质量之比m1∶m2＝1∶2，速度之比v1∶v2＝2∶1，当两车急刹车后，甲车滑行的最大距离为l1，乙车滑行的最大距离为l2，设两车与路面间的动摩擦因数相等，不计空气阻力，则(　D　)A．l1∶l2＝1∶2B．l1∶l2＝1∶1C．l1∶l2＝2∶1D．l1∶l2＝4∶1【解析】　由动能定理，对两车分别列式－F1l1＝0－m1v，－F2l2＝0－m2v，F1＝μm1g，F2＝μm2g.由以上四式联立得l1∶l2＝4∶1故选项D是正确的．6．一起重机的钢绳由静止开始匀加速提起质量为m的重物，当重物的速度为v1时，起重机的有用功率达到最大值P以后，起重机保持该功率不变，继续提升重物，直到以最大速度v2匀速上升为止，物体上升的高度为h，则整个过程中，下列说法正确的是(　BCD　)A．钢绳的最大拉力为B．钢绳的最大拉力为C．重物的最大速度v2＝D．重物匀加速运动的加速度为－g【解析】　由F－mg＝ma和P＝Fv可知，重物匀加速上升过程中钢绳拉力大于重力且不变，达到最大功率P后，随v增加，钢绳拉力F变小，当F＝mg时重物达最大速度v2，故v2＝，最大拉力F＝mg＋ma＝，A错误，B、C正确，由－mg＝ma得：a＝－g，D正确．7．如下图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°固定的粗糙斜面上，对物体施以平行于斜面向上的拉力F，t1＝1s时撤去拉力，物体运动的部分v－t图象如图乙，下列说法正确的是(g＝10m/s2)(B)A．拉力F的大小为20NB．物体运动到最高点的时间为3sC．0～1s内重力的平均功率为100WD．t＝4s时物体的速度大小为10m/s【解析】　由乙图可知，物体加速时，a1＝20m/s2，撤去F后，a2＝10m/s2，方向沿斜面向下，由牛顿第二定律得：F－mgsinθ－μmgcosθ＝ma1，mgsinθ＋μmgcosθ＝ma2，得：F＝30N，物体减速的时间t2＝＝2s，故B正确，A错误；mg＝mgsinθ·＝60W，C错误；物体至最高点后mgsinθ－μmgcosθ＝ma3，得a3＝2m/s2，故t＝4s时物体的速度v＝a3(t－3)＝2m/s，D错误．8．(2009年高考山东卷)右图示为某探究活动小组设计的节能运动系统．斜面轨道倾角为30°，质量为M的木箱与轨道的动摩擦因数为.木箱在轨道顶端时，自动装货装置将质量为m的货物装入木箱．然后木箱载着货物沿轨道无初速滑下，当轻弹簧被压缩至最短时，自动卸货装置立刻将货物卸下，然后木箱恰好被弹回到轨道顶端，再重复上述过程．下列选项正确的是(　BC　)A．m＝MB．m＝2MC．木箱不与弹簧接触时，上滑的加速度大于下滑的加速度D．在木箱与货物从顶端滑到最低点的过程中，减少的重力势能全部转化为弹簧的弹性势能【解析】　受力分析可知，下滑时加速度为g－μgcosθ，上滑时加速度为g＋μgcosθ，所以C正确；设下滑的距离为l，根据能量守恒有μ(m＋M)glcosθ＋μMglcosθ＝mglsinθ，得m＝2M，也可以根据除了重力、弹力做功以外，其他力(非重力、弹力)做的功之和等于系统机械能的变化量，A错误B正确；在木箱与货物从顶端滑到最低点的过程中，减少的重力势能转化为弹簧的弹性势能和内能，所以D不正确．9．带电荷量为＋q、质量为m的滑块，沿固定的斜面匀速下滑，现加上一竖直向上的匀强电场(如右图)，电场强度为E，且qE