【物理】2019届一轮复习人教版 　曲线运动　运动的合成与分解 学案 9页

第1讲　曲线运动　运动的合成与分解 板块一　主干梳理·夯实基础 ‎【知识点1】　曲线运动 ‎1．速度的方向：质点在某一点的速度方向，沿曲线上该点的切线方向。‎ ‎2．运动性质：做曲线运动的物体，速度的方向时刻改变，故曲线运动一定是变速运动，即必然具有加速度。‎ ‎3．物体做曲线运动的条件 ‎(1)运动学角度：物体的加速度方向跟速度方向不在同一条直线上。‎ ‎(2)动力学角度：物体所受合外力的方向跟速度方向不在同一条直线上。‎ ‎【知识点2】　运动的合成与分解　Ⅱ ‎1．基本概念 ‎(1)分运动和合运动：一个物体同时参与几个运动，参与的这几个运动即分运动，物体的实际运动即合运动。‎ ‎(2)运动的合成：已知分运动求合运动，包括位移、速度和加速度的合成。‎ ‎(3)运动的分解：已知合运动求分运动，解题时应按实际效果分解，或正交分解。‎ ‎2．遵循的规律：位移、速度、加速度都是矢量，故它们的合成与分解都遵循平行四边形法则。‎ ‎3．合运动的性质 ‎(1)两个匀速直线运动的合运动一定是匀速直线运动。‎ ‎(2)一个匀速直线运动、一个匀变速直线运动的合运动不一定(选填“一定”或“不一定”)是直线运动。‎ ‎(3)两个匀变速直线运动的合运动，不一定(选填“一定”或“不一定”)是匀变速直线运动。‎ 板块二　考点细研·悟法培优 考点1合运动的性质和轨迹[拓展延伸]‎ ‎1．运动类型的判断 ‎(1)判断物体是否做匀变速运动，要分析合力是否为恒力。‎ ‎(2)判断物体是否做曲线运动，要分析合力方向是否与速度方向成一定夹角。‎ ‎①当合力方向与速度方向的夹角为锐角时，物体的速率增大；‎ ‎②当合力方向与速度方向的夹角为钝角时，物体的速率减小；‎ ‎③当合力方向与速度方向垂直时，物体的速率不变。‎ ‎2．合运动的性质和轨迹的判断 ‎(1)根据加速度判定合运动的性质：若合加速度不变，则为匀变速运动；若合加速度(大小或方向)变化，则为非匀变速运动。‎ ‎(2)根据合加速度的方向与合初速度的方向判定合运动的轨迹：若合加速度的方向与合初速度的方向在同一直线上则为直线运动，否则为曲线运动。‎ ‎(3)合力(或合加速度)方向与轨迹的关系 无力不拐弯，拐弯必有力。‎ 物体做曲线运动的轨迹一定夹在合力(或合加速度)方向和速度方向之间，速度方向与轨迹相切，合力(或合加速度)方向指向曲线的凹侧。‎ 例1　(多选)如图所示，物体在恒定外力F的作用下沿曲线从A运动到B，此时突然使物体受到的力F反向，大小不变，则关于物体以后的运动情况，下列说法中正确的是(　　)‎ A．物体不可能沿曲线Ba运动 B．物体不可能沿直线Bb运动 C．物体不可能沿曲线Bc运动 D．物体不可能沿原曲线由B返回A ‎ (1)物体做曲线运动的条件是什么？‎ 提示：有初速度，且受到与初速度不在一条线上的合外力。‎ ‎(2)合力方向与轨迹的关系是什么？‎ 提示：合力方向指向轨迹凹侧。‎ 尝试解答　选ABD。‎ 物体从A点向B点做曲线运动，所受合外力可能的方向如图所示。由于物体所受的力是恒力，所以任何一种可能的情况中力的方向也不能和过B点的切线Bb平行，那么当力F突然反向时，物体受的力也不可能与Bb直线平行，所以物体不可能沿过B点的切线Bb做直线运动，物体仍做曲线运动，故B选项正确；由于合外力方向的变化，必然导致曲线弯曲的方向与原来相反，因此，物体在所受力变向后沿曲线Bc运动是可能的，C不正确，A、B、D正确。‎ 总结升华 决定物体运动的两因素 决定物体运动的因素一是初速度，二是合力，而物体运动的轨迹在合力与速度方向的夹角范围内，且弯向受力方向，这是分析该类问题的技巧。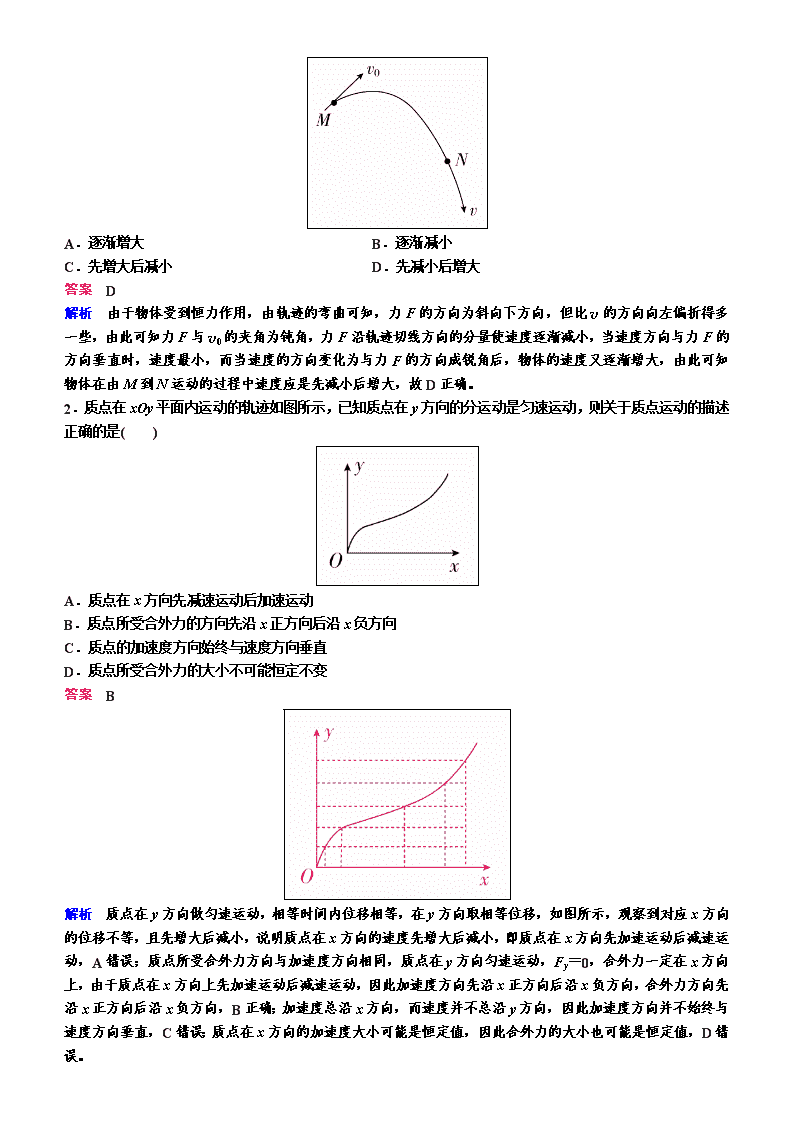‎ 1.一个物体在光滑水平面上以初速度v0做曲线运动，已知此过程中水平方向只受一个恒力的作用，运动轨迹如图所示，M点的速度为v0，则由M到N的过程中，速度大小的变化为(　　)‎ A．逐渐增大 B．逐渐减小 C．先增大后减小 D．先减小后增大 答案　D 解析　由于物体受到恒力作用，由轨迹的弯曲可知，力F的方向为斜向下方向，但比v的方向向左偏折得多一些，由此可知力F与v0的夹角为钝角，力F沿轨迹切线方向的分量使速度逐渐减小，当速度方向与力F的方向垂直时，速度最小，而当速度的方向变化为与力F的方向成锐角后，物体的速度又逐渐增大，由此可知物体在由M到N运动的过程中速度应是先减小后增大，故D正确。‎ ‎2．质点在xOy平面内运动的轨迹如图所示，已知质点在y方向的分运动是匀速运动，则关于质点运动的描述正确的是(　　)‎ A．质点在x方向先减速运动后加速运动 B．质点所受合外力的方向先沿x正方向后沿x负方向 C．质点的加速度方向始终与速度方向垂直 D．质点所受合外力的大小不可能恒定不变 答案　B 解析　质点在y方向做匀速运动，相等时间内位移相等，在y方向取相等位移，如图所示，观察到对应x方向的位移不等，且先增大后减小，说明质点在x方向的速度先增大后减小，即质点在x方向先加速运动后减速运动，A错误；质点所受合外力方向与加速度方向相同，质点在y方向匀速运动，Fy＝0，合外力一定在x方向上，由于质点在x方向上先加速运动后减速运动，因此加速度方向先沿x正方向后沿x负方向，合外力方向先沿x正方向后沿x负方向，B正确；加速度总沿x方向，而速度并不总沿y方向，因此加速度方向并不始终与速度方向垂直，C错误；质点在x方向的加速度大小可能是恒定值，因此合外力的大小也可能是恒定值，D错误。‎ 考点2运动的合成与分解[深化理解]‎ ‎1．合运动和分运动的关系 ‎(1)等时性：各个分运动与合运动总是同时开始，同时结束，经历时间相等(不同时的运动不能合成)。‎ ‎(2)独立性：一个物体同时参与几个分运动时，各分运动独立进行，互不影响。‎ ‎(3)等效性：各分运动叠加起来与合运动有完全相同的效果。‎ ‎(4)同一性：各分运动与合运动是指同一物体参与的分运动和实际发生的运动，不能是几个不同物体发生的不同运动。‎ ‎2．运动的合成与分解的运算法则：运动的合成与分解是指描述运动的各物理量即位移、速度、加速度的合成与分解，由于它们均是矢量，故合成与分解都遵守平行四边形定则。‎ 例2　[2017·太原模拟](多选)如图在灭火抢险的过程中，消防队员有时要借助消防车上的梯子爬到高处进行救人或灭火作业。为了节省救援时间，在消防车向前前进的过程中，人同时相对梯子匀速向上运动。在地面上看消防队员的运动，下列说法中正确的是(　　)‎ A．当消防车匀速前进时，消防队员一定做匀加速直线运动 B．当消防车匀速前进时，消防队员一定做匀速直线运动 C．当消防车匀加速前进时，消防队员一定做匀变速曲线运动 D．当消防车匀加速前进时，消防队员一定做匀变速直线运动 ‎ (1)消防员同时参与了哪两个分运动？‎ 提示：沿梯子向上和随车前进。‎ ‎(2)两个直线运动的合运动是什么运动取决于什么？‎ 提示：合初速度与合加速度的方向。‎ 尝试解答　选BC。‎ 两个互成角度的匀速直线运动的合运动仍然是匀速直线运动，一个匀速直线运动与一个匀变速直线运动的合运动是匀变速曲线运动。当消防车匀速前进时，消防队员一定做匀速直线运动，B正确，A错误；当消防车匀加速前进时，消防队员一定做匀变速曲线运动，C正确，D错误。‎ 总结升华 求解运动的合成与分解的技巧 ‎(1)求解运动的合成与分解问题，应抓住合运动与分运动具有等时性、独立性。‎ ‎(2)物体的实际运动是合运动。‎ 　[2017·北京海淀区期中](多选)某同学在研究运动的合成时做了如图所示活动：用左手沿黑板推动直尺竖直向上运动，运动中保持直尺水平，同时，用右手沿直尺向右移动笔尖。若该同学左手的运动为匀速运动，右手相对于直尺的运动为初速度为零的匀加速运动，则关于笔尖的实际运动，下列说法中正确的是(　　)‎ A．笔尖做匀速直线运动 B．笔尖做匀变速直线运动 C．笔尖做匀变速曲线运动 D．笔尖的速度方向与水平方向夹角逐渐变小 答案　CD 解析　笔尖同时参与了向右的初速度为零的匀加速运动，竖直向上的匀速运动，所以合运动是匀变速曲线运动，速度合成如图所示，则tanθ＝，v1逐渐变大，θ变小，故C、D正确。‎ 考点3关联速度问题[解题技巧]‎ ‎1．模型特点 沿绳(或杆)方向的速度分量大小相等。‎ ‎2．思路与方法 合速度→物体的实际运动速度v 分速度→ 方法：v1与v2的合成遵循平行四边形定则。‎ 例3　如图所示，细线一端固定在天花板上的O点，另一端穿过一张CD光盘的中央小孔后拴着一个橡胶球，橡胶球静止时，竖直悬线刚好挨着水平桌面的边沿。现将CD光盘按在桌面上，并沿桌面边缘以速度v匀速移动，移动过程中，CD光盘中央小孔始终紧挨桌面边线，当悬线与竖直方向的夹角为θ时，小球上升的速度大小为(　　)‎ A．vsinθ B．vcosθ C．vtanθ D．vcotθ ‎ (1)哪个速度是合速度？‎ 提示：光盘向右的速度。‎ ‎(2)小球上升的速度和哪个速度相等？‎ 提示：沿绳分速度。‎ 尝试解答　选A。‎ 将光盘水平向右移动的速度v分解为沿细线方向的速度和垂直于细线方向的速度，而小球上升的速度大小与速度v沿细线方向的分速度大小相等，故可得：v球＝vsinθ，A正确。‎ 总结升华 关联速度问题常见模型 把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)的两个分量，根据沿绳(杆)方向的分速度大小相等求解。常见的模型如图所示。‎ 　[2017·太原模拟]如图所示，开始时A、B间的细绳呈水平状态，现由计算机控制物体A的运动，使其恰好以速度v沿竖直杆匀速下滑，经细绳通过定滑轮拉动物体B在水平面上运动，则下列vt图象中，最接近物体B的运动情况的是(　　)‎ 答案　A 解析　A向下运动为合运动，将它分解成沿绳的v1和垂直绳的v2，B的速度等于v1，设v1与v夹角为θ，则v1＝vcosθ，θ变小，cosθ变大，v1变大，但变化的越来越慢，故A正确。‎ ‎1．模型构建 在运动的合成与分解问题中，两个匀速直线运动的合运动仍是匀速直线运动，其中一个速度大小和方向都不变，另一个速度大小不变，方向在180°范围内(在速度不变的分运动所在直线的一侧)变化。我们对合运动或分运动的速度、时间、位移等问题进行研究。这样的运动系统可看作“小船渡河模型”。‎ ‎2．模型条件 ‎(1)物体同时参与两个匀速直线运动。‎ ‎(2)一个分运动速度大小和方向保持不变，另一个分运动速度大小不变，方向可在一定范围内变化。‎ ‎3．模型特点 ‎(1)船的实际运动是水流的运动和船相对静水的运动的合运动。‎ ‎(2)三种速度：船在静水中的速度v1、水的流速v2、船的实际速度v。‎ ‎(3)三种情景 ‎①过河时间最短：船头正对河岸，渡河时间最短，t短＝(d为河宽)。‎ ‎②过河路径最短(v2v1时)：合速度不可能垂直于河岸，无法垂直河岸渡河。确定方法如下：如图所示，以v2矢量末端为圆心，以v1矢量的大小为半径画弧，从v2‎ 矢量的始端向圆弧作切线，则合速度沿此切线方向航程最短。由图可知sinθ＝，最短航程x短＝＝d。‎ ‎[2018·合肥检测]有一条两岸平直、河水均匀流动，流速恒为v的大河，一条小船渡河，去程时船头指向始终与河岸垂直，回程时行驶路线与河岸垂直，小船在静水中的速度大小为，回程与去程所用时间之比为(　　)‎ A．3∶2 B．2∶1 ‎ C．3∶1 D．2∶1‎ ‎[答案]　B ‎[解析]　设河宽为d，则去程所用的时间t1＝＝；回程时的合速度：v′＝＝，回程的时间为：t2＝＝；故回程与去程所用时间之比为t2∶t1＝2∶1，B正确。‎ 名师点睛 求解小船渡河问题的方法 求解小船渡河问题有两类：一是求渡河时间，二是求渡河位移。无论哪类都必须明确以下四点：‎ ‎(1)解决这类问题的关键：正确区分分运动和合运动，船的航行方向也就是船头指向，是分运动。船的运动方向也就是船的实际运动方向，是合运动，一般情况下与船头指向不一致。‎ ‎ (2)运动分解的基本方法，按实际效果分解，一般用平行四边形定则按水流方向和船头指向分解。‎ ‎(3)渡河时间只与垂直河岸的船的分速度有关，与水流速度无关。求解渡河时间，一般根据运动的独立性t＝＝＝。‎ ‎(4)求最短渡河位移时，当水速小于船速时即为河宽，当水速大于船速时，根据船速v船与水流速度v水的情况用三角形法则求极限的方法处理。‎ ‎[2017·四川成都模拟]如图所示，小船以大小为v1、方向与上游河岸成θ的速度(在静水中的速度)从A处过河，经过时间t正好到达正对岸的B处。现要使小船在更短的时间内过河并且也正好到达正对岸B处，在水流速度不变的情况下，可采取下列方法中的哪一种(　　)‎ A．只要增大v1大小，不必改变θ角 B．只要增大θ角，不必改变v1大小 C．在增大v1的同时，也必须适当增大θ角 D．在增大v1的同时，也必须适当减小θ角 答案　C 解析　若只增大v1大小，不必改变θ角，则船在水流方向的分速度增大，因此船不可能垂直达到对岸，故A错误；若只增大θ角，不必改变v1大小，同理可知，水流方向的分速度在减小，而垂直河岸的分速度在增大，船不可能垂直到达对岸，故B错误；若在增大v1的同时，也适当增大θ角，保证水流方向的分速度不变，而垂直河岸的分速度在增大，则船能垂直达到对岸，且时间更短，故C正确；若增大v1的同时，也减小θ角，则水流方向的分速度增大，不能垂直到达对岸，故D错误。‎