【物理】2020届一轮复习人教版竖直平面内(斜面内)的圆周运动学案 7页

‎2020届一轮复习人教版 竖直平面内(斜面内)的圆周运动 学案 ‎1．竖直面内圆周运动的两个基本模型的比较 轻绳模型 轻杆模型 最高点 受力 特征 除重力外，物体可能受到向下或等于零的弹力 除重力外，物体可能受到向下、等于零或向上的弹力 受力 示意图 力学 方程 mg＋FT＝m mg±FN＝m 临界 特征 FT＝0，即mg＝m，即vmin＝ v＝0时F向＝0，即FN＝mg v＝‎ 的意义 物体能否过最高点的临界点 FN表现为拉力还是支持力的临界点 ‎2．解题技巧 ‎(1)定模型：首先判断是轻绳模型还是轻杆模型，两种模型过最高点的临界条件不同。‎ ‎(2)确定临界点：抓住绳模型中最高点v≥及杆模型中v≥0这两个临界条件。‎ ‎(3)研究状态：通常情况下竖直平面内的圆周运动只涉及最高点和最低点的运动情况。‎ ‎(4)受力分析：对物体在最高点或最低点时进行受力分析，根据牛顿第二定律列出方程：F合＝F向。‎ ‎(5)过程分析：应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程。‎ 模型1　绳—球模型 ‎[例1]　 如图所示，一质量为m＝‎0.5 kg的小球，用长为‎0.4 m的轻绳拴着在竖直平面内做圆周运动。g取‎10 m/s2，求：‎ ‎(1)小球要做完整的圆周运动，在最高点的速度至少为多大？‎ ‎(2)当小球在最高点的速度为‎4 m/s时，轻绳拉力多大？‎ ‎(3)若轻绳能承受的最大张力为45 N，小球的速度不能超过多大？‎ 解析(1)在最高点，对小球受力分析如图甲，由牛顿第二定律得mg＋F1＝m①‎ 由于轻绳对小球只能提供指向圆心的拉力，即F1不可能取负值，亦即F1≥0②‎ 联立①②得v≥，‎ 代入数值得v≥‎2 m/s 所以，小球要做完整的圆周运动，在最高点的速度至少为‎2 m/s。‎ ‎(2)对小球，由牛顿第二定律得mg＋F2＝m，‎ 将v2＝‎4 m/s代入得，F2＝15 N。‎ ‎(3)由分析可知，小球在最低点时轻绳张力最大，对小球受力分析如图乙，由牛顿第二定律得 F3－mg＝m③‎ 又F3≤45 N④‎ 联立③④得v3≤‎4 m/s，所以小球的速度不能超过‎4 m/s。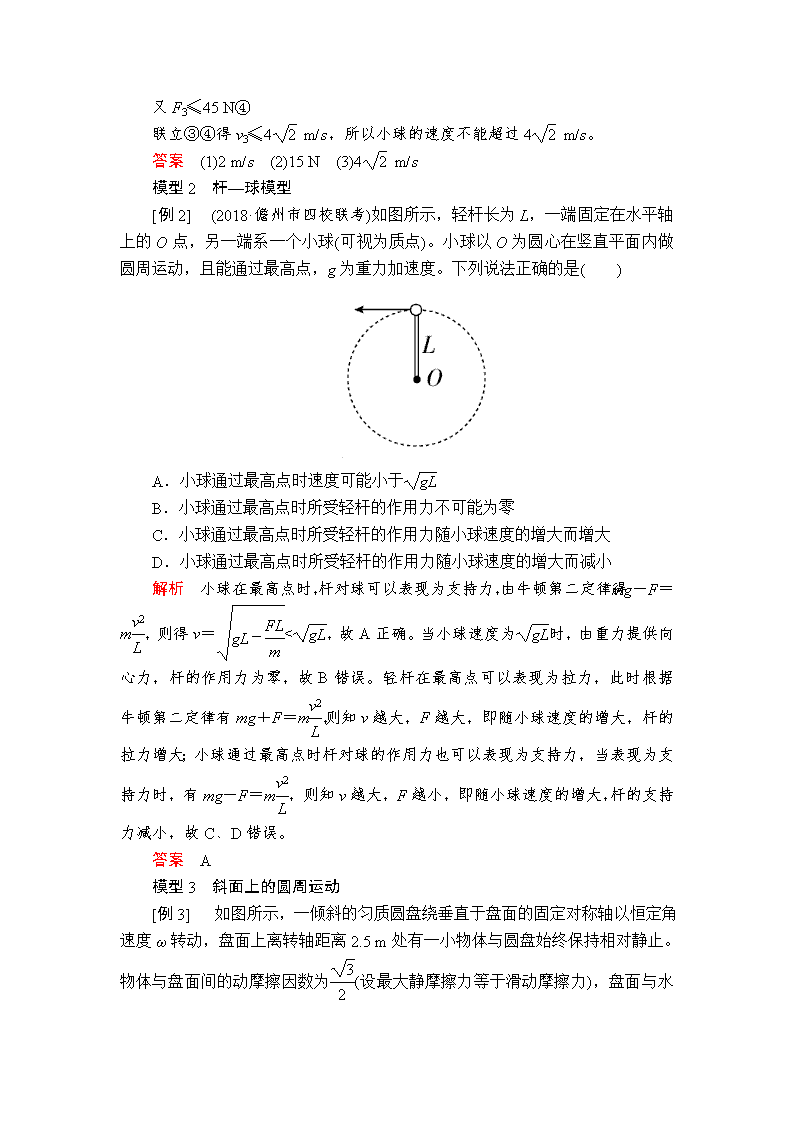‎ 答案　(1)‎2 m/s　(2)15 N　(3)‎4 m/s 模型2　杆—球模型 ‎[例2]　 (2018·儋州市四校联考)如图所示，轻杆长为L，一端固定在水平轴上的O点，另一端系一个小球(可视为质点)。小球以O为圆心在竖直平面内做圆周运动，且能通过最高点，g为重力加速度。下列说法正确的是(　　)‎ A．小球通过最高点时速度可能小于 B．小球通过最高点时所受轻杆的作用力不可能为零 C．小球通过最高点时所受轻杆的作用力随小球速度的增大而增大 D．小球通过最高点时所受轻杆的作用力随小球速度的增大而减小 解析　小球在最高点时，杆对球可以表现为支持力，由牛顿第二定律得：mg－F＝m，则得v＝<，故A正确。当小球速度为时，由重力提供向心力，杆的作用力为零，故B错误。轻杆在最高点可以表现为拉力，此时根据牛顿第二定律有mg＋F＝m，则知v越大，F越大，即随小球速度的增大，杆的拉力增大；小球通过最高点时杆对球的作用力也可以表现为支持力，当表现为支持力时，有mg－F＝m，则知v越大，F越小，即随小球速度的增大，杆的支持力减小，故C、D错误。‎ 答案　A 模型3　斜面上的圆周运动 ‎[例3]　 如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω转动，盘面上离转轴距离‎2.5 m 处有一小物体与圆盘始终保持相对静止。物体与盘面间的动摩擦因数为(设最大静摩擦力等于滑动摩擦力)，盘面与水平面的夹角为30°，g取‎10 m/s2。则ω的最大值是(　　)‎ A. rad/s B. rad/s C．1.0 rad/s D．0.5 rad/s 解析　物体随圆盘做圆周运动，运动到最低点时最容易滑动，因此物体在最低点且刚好要滑动时的转动角速度为最大值，这时，根据牛顿第二定律有，μmgcos30°－mgsin30°＝mrω2，求得ω＝1.0 rad/s，C正确，A、B、D错误。‎ 答案　C 方法感悟 ‎1．求解斜面上的圆周运动问题时，注意对物体所受重力沿斜面方向的分力以及沿斜面方向的静摩擦力进行分析，注意静摩擦力的方向是可变的。‎ ‎2．斜面上圆周运动的临界问题 在斜面上做圆周运动的物体，因所受的控制因素不同，如静摩擦力控制、轻绳控制、轻杆控制，物体的受力情况和所遵循的规律也不相同。解决方法可参照水平面内圆周运动和竖直面内的圆周运动临界问题的解决方法。‎ ‎(1)静摩擦力控制下的圆周运动 ‎(2)轻绳控制下的圆周运动 ‎(3)轻杆控制下的圆周运动 ‎1. 如图所示，长均为L的两根轻绳一端共同系住质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间的距离也为L。重力加速度大小为g。现使小球在竖直平面内以AB为轴做圆周运动，若小球在最高点速率为v时，两根绳的拉力恰好均为零，则小球在最高点速率为2v时，每根绳的拉力大小为(　　)‎ A.mg B.mg C．3mg D．2mg 答案　A 解析　设小球在竖直面内做圆周运动的半径为r，小球运动到最高点时轻绳与圆周运动轨道平面的夹角为θ＝30°，则有r＝Lcosθ＝L。根据题述，小球在最高点速率为v时，两根绳的拉力恰好均为零，有mg＝m；小球在最高点速率为2‎ v时，设每根绳的拉力大小为F，则有2Fcosθ＋mg＝m，联立解得F＝mg，A正确。‎ ‎2. 如图所示，小球在竖直放置的光滑圆形管道内做圆周运动，内侧壁半径为R，小球半径为r，则下列说法中正确的是(　　)‎ A．小球通过最高点时的最小速度vmin＝ B．小球通过最高点时的最小速度vmin＝ C．小球在水平线ab以下的管道中运动时，内侧管壁对小球一定无作用力 D．小球在水平线ab以上的管道中运动时，外侧管壁对小球一定有作用力 答案　C 解析　因是在圆形管道内做圆周运动，所以在最高点时，内壁可以给小球沿半径向外的支持力，所以小球通过最高点时的最小速度为零，故A、B错误；小球在水平线ab以下的管道中运动时，竖直向下的重力沿半径方向的分力沿半径方向向外，小球的向心力是沿半径指向圆心的，小球与外壁一定会相互挤压，所以小球一定会受到外壁的作用力，内侧管壁对小球一定无作用力，故C正确；小球在水平线ab以上的管道中运动时，当速度较小时，重力沿半径方向上的分力大于或等于小球做圆周运动需要的向心力，此时小球与外壁不存在相互挤压，外侧管壁对小球没有作用力，故D错误。‎ ‎3. (多选)如图所示，两个质量均为m的小物块a和b(可视为质点)静止在倾斜的匀质圆盘上，圆盘可绕垂直于盘面的固定轴转动，a到转轴的距离为l，b到转轴的距离为‎2l，物块与盘面间的动摩擦因数为，盘面与水平面的夹角为30°。设最大静摩擦力等于滑动摩擦力，重力加速度大小为g，若a、b随圆盘以角速度ω 匀速转动，下列说法中正确的是(　　)‎ A．a在最高点时所受摩擦力可能为0‎ B．a在最低点时所受摩擦力可能为0‎ C．ω＝ 是a开始滑动的临界角速度 D．ω＝ 是b开始滑动的临界角速度 答案　AD 解析　a在最高点时可能由重力沿斜面的分力提供向心力，所以所受摩擦力可能为0，故A正确；a在最低点，由牛顿运动定律f－mgsinθ＝m，所以a在最低点时所受摩擦力不可能为0，故B错误；对a在最低点，由牛顿运动定律μmgcosθ－mgsinθ＝mω‎2l，代入数据解得ω＝，故C错误；对b在最低点，由牛顿运动定律μmgcosθ－mgsinθ＝mω2(‎2l)，代入数据解得ω＝ ，故D正确。‎