高三物理一轮复习第4章曲线运动万有引力与航天第3节圆周运动教师用书 11页

第 3 节 圆周运动 考点一| 圆周运动的基本概念 1．线速度：描述物体圆周运动快慢的物理量． v＝Δs Δt ＝2πr T . 2．角速度：描述物体绕圆心转动快慢的物理量． ω＝Δθ Δt ＝2π T . 3．周期和频率：描述物体绕圆心转动快慢的物理量． T＝2πr v ，T＝1 f . 4．向心加速度：描述速度方向变化快慢的物理量． an＝v2 r ＝rω2＝ωv＝4π2 T2 r. 5．相互关系：(1)v＝ωr＝2π T r＝2πrf. (2)an＝v2 r ＝rω2＝ωv＝4π2 T2 r＝4π2f2r. 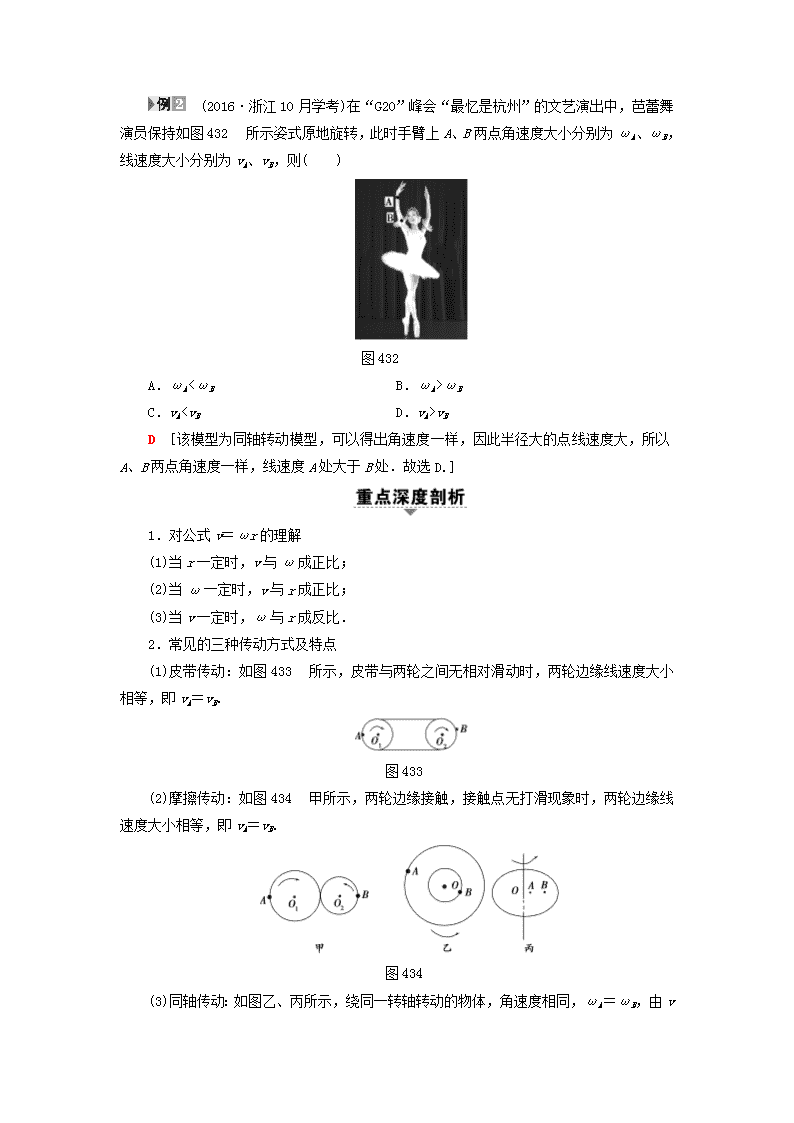(2016·浙江 4 月学考)如图 431 为某中国运动员在短道速滑比赛中勇夺金牌 的精彩瞬间．假定此时他正沿圆弧形弯道匀速率滑行，则他( ) 图 431 A．所受的合力为零，做匀速运动 B．所受的合力恒定，做匀加速运动 C．所受的合力恒定，做变加速运动 D．所受的合力变化，做变加速运动 D [运动员做匀速圆周运动，其加速度指向圆心，方向时刻变化，为变加速运动，合力 也指向圆心，方向时刻变化．D 正确．] (2016·浙江 10 月学考)在“G20”峰会“最忆是杭州”的文艺演出中，芭蕾舞 演员保持如图 432 所示姿式原地旋转，此时手臂上 A、B 两点角速度大小分别为ωA、ωB， 线速度大小分别为 vA、vB，则( ) 图 432 A．ωA<ωB B．ωA>ωB C．vAvB D [该模型为同轴转动模型，可以得出角速度一样，因此半径大的点线速度大，所以 A、 B 两点角速度一样，线速度 A 处大于 B 处．故选 D.] 1．对公式 v＝ωr 的理解 (1)当 r 一定时，v 与ω成正比； (2)当ω一定时，v 与 r 成正比； (3)当 v 一定时，ω与 r 成反比． 2．常见的三种传动方式及特点 (1)皮带传动：如图 433 所示，皮带与两轮之间无相对滑动时，两轮边缘线速度大小 相等，即 vA＝vB. 图 433 (2)摩擦传动：如图 434 甲所示，两轮边缘接触，接触点无打滑现象时，两轮边缘线 速度大小相等，即 vA＝vB. 图 434 (3)同轴传动：如图乙、丙所示，绕同一转轴转动的物体，角速度相同，ωA＝ωB，由 v ＝ωr 知 v 与 r 成正比． 1．对于做匀速圆周运动的物体，下列说法中不正确的是( ) A．相等的时间内通过的路程相等 B．相等的时间内通过的弧长相等 C．相等的时间内通过的位移相等 D．相等的时间内转过的角度相等 C [匀速圆周运动是指线速度大小不变的圆周运动，因此在相等时间内通过路程相等， 弧长相等，转过的角度也相等，故选项 A、B、D 正确；相等的时间内通过的位移方向不同， 由于位移是矢量，因此位移不相等，故选项 C 错误．] 2.皮带传动装置如图 435 所示，两轮的半径不相等，传动过程中皮带不打滑．关于两 轮边缘上的点，下列说法正确的是( ) 图 435 【导学号：81370156】 A．周期相同 B．角速度相等 C．线速度大小相等 D．向心加速度相等 C [皮带不打滑时，皮带上各点的线速度大小相等，C 正确．] 3.如图 436 所示，当正方形薄板绕着过其中心 O 并与板垂直的转动轴转动时，板上 A、 B 两点( ) 图 436 A．角速度之比ωA∶ωB＝ 2∶1 B．角速度之比ωA∶ωB＝1∶ 2 C．线速度之比 vA∶vB＝ 2∶1 D．线速度之比 vA∶vB＝1∶ 2 D [板上 A、B 两点的角速度相等，角速度之比ωA∶ωB＝1∶1，选项 A、B 错误；线速 度 v＝ωr，线速度之比 vA∶vB＝1∶ 2，选项 C 错误，D 正确．] 4．(加试要求)如图 437 是自行车传动装置的示意图，其中Ⅰ是半径为 r1 的大齿轮， Ⅱ是半径为 r2 的小齿轮，Ⅲ是半径为 r3 的后轮，假设脚踏板的转速为 n r/s，则自行车前进 的速度为( ) 图 437 A.πnr1r3 r2 B.πnr2r3 r1 C.2πnr2r3 r1 D.2πnr1r3 r2 D [因为要计算自行车前进的速度，即车轮Ⅲ边缘上的线速度的大小，根据题意知：轮 Ⅰ和轮Ⅱ边缘上的线速度的大小相等，据 v＝rω可知：r1ω1＝r2ω2，已知ω1＝ω，则轮Ⅱ 的角速度ω2＝r1 r2 ω，因为轮Ⅱ和轮Ⅲ共轴，所以转动的角速度相等即ω3＝ω2，根据 v＝rω 可知，v3＝r3ω3＝ωr1r3 r2 ＝2πnr1r3 r2 .] 考点二| 圆周运动中的动力学分析 1．匀速圆周运动的向心力 (1)作用效果 向心力产生向心加速度，只改变速度的方向，不改变速度的大小． (2)大小 F＝mv2 r ＝mω2r＝m4π2 T2 r＝mωv＝4π2mf2r. (3)方向 始终沿半径方向指向圆心，时刻在改变，即向心力是一个变力． (4)来源(加试要求) 向心力可以由一个力提供，也可以由几个力的合力提供，还可以由一个力的分力提供． 2．离心现象的受力特点(只必考要求) 图 438 当 F＝mrω2 时，物体做匀速圆周运动； 当 F＝0 时，物体沿切线方向飞出；当 FFC D．FB>FC B [在平直公路上行驶时，重力等于支持力，由牛顿第三定律知，压力等于支持力，所 以压力 FA＝mg；汽车到达 B 点时，有向下的加速度，汽车失重，故支持力小于重力，因而压 力小于重力；在 C 点时与在 B 点时相反，压力大于重力，所以 FC>FA>FB，故 B 正确．] 2．(2017·通化高三检测)如图 4310 所示，在匀速转动的圆筒内壁上紧靠着一个物体 一起运动，充当向心力的是( ) 图 4310 A．重力 B．弹力 C．静摩擦力 D．滑动摩擦力 B [物体在竖直方向上受重力和静摩擦力作用，两力平衡，在水平方向上受弹力作用， 弹力充当向心力，B 正确．] 3．(2017·绍兴市调研)奥运会单杠比赛中有一个“单臂大回环”的动作，难度系数非 常大．假设运动员质量为 m，单臂抓杠杆身体下垂时，手掌到人体重心的距离为 l.如图 4311 所示，在运动员单臂回转从顶点倒立转至最低点过程中，可将人体视为质量集中于重心的质 点，且不考虑手掌与单杠间的摩擦力，重力加速度为 g，若运动员在最低点的速度为 2 gl， 则运动员的手臂拉力为自身重力的( ) 【导学号：81370158】 图 4311 A．2 倍 B．3 倍 C．4 倍 D．5 倍 D [对运动员在最低点受力分析，由牛顿第二定律可得，F－mg＝mv2 l ，解得，F＝5mg， D 项正确．] 4．(加试要求)在云南省某些地方到现在还要依靠滑铁索过江，若把这滑铁索过江简化 成如图 4312 所示的模型，铁索的两个固定点 A、B 在同一水平面内，A、B 间的距离为 L ＝80 m，铁索的最低点离 A、B 连线的垂直距离为 H＝8 m，若把铁索看做是圆弧，已知一质 量 m＝52 kg 的人借助滑轮(滑轮质量不计)滑到最低点时的速度为 10 m/s，那么( ) 图 4312 A．人在整个铁索上的运动可看成是匀速圆周运动 B．可求得铁索的圆弧半径为 100 m C．人在滑到最低点时，滑轮对铁索的压力为 570 N D．人在滑到最低点时，滑轮对铁索的压力为 50 N C [人借助滑轮下滑过程中，其速度是逐渐增大的，因此人在整个铁索上的运动不能看 成匀速圆周运动；设圆弧的半径为 r，由几何关系，有：(r－H)2＋ L 2 2＝r2，解得 r＝104 m； 人在滑到最低点时，根据牛顿第二定律得：FN－mg＝mv2 r ，解得 FN＝570 N，选项 C 正确．] 考点三| 竖直面内圆周运动的临界问题 1．在竖直平面内做圆周运动的物体，按运动到轨道最高点时的受力情况可分为两类： 一是无支撑(如球与绳连接、沿内轨道运动的过山车等)，称为“绳(环)约束模型”，二是有 支撑(如球与杆连接、在弯管内的运动等)，称为“杆(管)约束模型”． 2．绳、杆模型涉及的临界问题 绳模型 杆模型 常见类型 过最高点的 临界条件 由 mg＝m v2 r 得 v 临＝ gr 由小球恰能做圆周运动得 v 临＝0 讨论分析 (1)过最高点时，v≥ gr，FN＋mg ＝mv2 r ，绳、圆轨道对球产生弹力 FN (2)不能过最高点时，v< gr，在到 (1)当 v＝0 时，FN＝mg，FN 为支持力， 沿半径背离圆心 (2)当 0 gr时，FN＋mg＝mv2 r ，FN 指向圆 心并随 v 的增大而增大 (2016·浙江 4 月学考)如图 4313 所示，装置由一理想弹簧发射器及两个轨 道组成．其中轨道Ⅰ由光滑轨道 AB 与粗糙直轨道 BC 平滑连接，高度差分别是 h1＝0.20 m、 h2＝0.10 m，BC 水平距离 L＝1.00 m．轨道Ⅱ由 AE、螺旋圆形 EFG 和 GB 三段光滑轨道平滑 连接而成，且 A 点与 F 点等高．当弹簧压缩量为 d 时，恰能使质量 m＝0.05 kg 的滑块沿轨 道Ⅰ上升到 B 点；当弹簧压缩量为 2d 时，恰能使滑块沿轨道Ⅰ上升到 C 点．(已知弹簧弹性 势能与压缩量的平方成正比) 图 4313 当弹簧压缩量为 d 时，若沿轨道Ⅱ运动，滑块能否上升到 B 点？请通过计算说明理由. 【导学号：81370159】 【解析】 恰能通过圆环最高点，需满足的条件是 mg＝mv2 Rm ① 由弹簧压缩量为 d 时，恰好使滑块上升到 B 点得 EpA＝mgh1 ② 沿轨道Ⅱ运动时由 A 到 F 机械能守恒 EpA＝1 2 mv2 ③ ①②③联立解得 v＝2 m/s，Rm＝0.4 m 当 R>Rm＝0.4 m 时，滑块会脱离螺旋轨道，不能上升到 B 点． 【答案】 见解析 1．(多选)(2016·台州市六校高二联考)如图 4314 所示甲、乙、丙、丁是游乐场中比 较常见的过山车，甲、乙两图的轨道车在轨道的外侧做圆周运动，丙、丁两图的轨道车在轨 道的内侧做圆周运动，两种过山车都有安全锁(由上、下、侧三个轮子组成)把轨道车套在了 轨道上，四个图中轨道的半径都为 R，下列说法正确的是( ) 图 4314 A．甲图中，当轨道车以一定的速度通过轨道最高点时，座椅一定给人向上的力 B．乙图中，当轨道车以一定的速度通过轨道最低点时，安全带一定给人向上的力 C．丙图中，当轨道车以一定的速度通过轨道最低点时，座椅一定给人向上的力 D．丁图中，轨道车过最高点的最小速度为 gR BC [在甲图中，当速度比较小时，根据牛顿第二定律得，mg－FN＝mv2 R ，即座椅给人施 加向上的力，当速度比较大时，根据牛顿第二定律得，mg＋FN＝mv2 R ，即座椅给人施加向下的 力，故 A 错误；在乙图中，因为合力指向圆心，重力竖直向下，所以安全带一定给人向上的 力，故 B 正确；在丙图中，当轨道车以一定的速度通过轨道最低点时，合力方向向上，重力 竖直向下，则座椅给人的作用力一定竖直向上，故 C 正确；在丁图中，由于轨道车有安全锁， 可知轨道车在最高点的最小速度为零，故 D 错误．] 2．(2017·东阳模拟)一轻杆一端固定质量为 m 的小球，以另一端 O 为圆心，使小球在 竖直面内做半径为 R 的圆周运动，如图 4315 所示，则下列说法正确的是( ) 图 4315 【导学号：81370160】 A．小球过最高点时，杆所受到的弹力可以等于零 B．小球过最高点的最小速度是 gR C．小球过最高点时，杆对球的作用力一定随速度增大而增大 D．小球过最高点时，杆对球的作用力一定随速度增大而减小 A [轻杆可对小球产生向上的支持力，小球经过最高点的速度可以为零，当小球过最高 点的速度 v＝ gR时，杆所受的弹力等于零，A 正确，B 错误；若 v< gR，则杆在最高点对小 球的弹力竖直向上，mg－F＝mv2 R ，随 v 增大，F 减小，若 v> gR，则杆在最高点对小球的弹 力竖直向下，mg＋F＝mv2 R ，随 v 增大，F 增大，故 C、D 均错误．] 3．长度为 1 m 的轻杆 OA 的 A 端有一质量为 2 kg 的小球，以 O 点为圆心，在竖直平面 内做圆周运动，如图 4316 所示，小球通过最高点时的速度为 3 m/s，g 取 10 m/s2，则此 时小球将( ) 图 4316 A．受到 18 N 的拉力 B．受到 38 N 的支持力 C．受到 2 N 的拉力 D．受到 2 N 的支持力 D [设此时轻杆拉力大小为 F，根据向心力公式有 F＋mg＝mv2 r ，代入数值可得 F＝－2 N， 表示受到 2 N 的支持力，选项 D 正确．] 4.如图 4317 所示，小球紧贴在竖直放置的光滑圆形管道内壁做圆周运动，内侧壁半 径为 R，小球半径为 r，则下列说法正确的是( ) 图 4317 【导学号：81370161】 A．小球通过最高点时的最小速度 vmin＝ g R＋r B．小球通过最高点时的最小速度 vmin＝ gR C．小球在水平线 ab 以下的管道中运动时，内侧管壁对小球一定无作用力 D．小球在水平线 ab 以上的管道中运动时，外侧管壁对小球一定有作用力 C [小球沿光滑圆形管道上升，到达最高点的速度可以为零，A、B 选项均错误；小球在水 平线 ab 以下的管道中运动时，由于重力的方向竖直向下，向心力方向斜向上，必须受外侧 管壁指向圆心的作用力，C 正确；小球在水平线 ab 以上的管道中运动时，由于重力有指向 圆心的分量，若速度较小，小球可不受外侧管壁的作用力，D 错误．]