【物理】2019届一轮复习人教版交变电流的产生及描述教案 7页

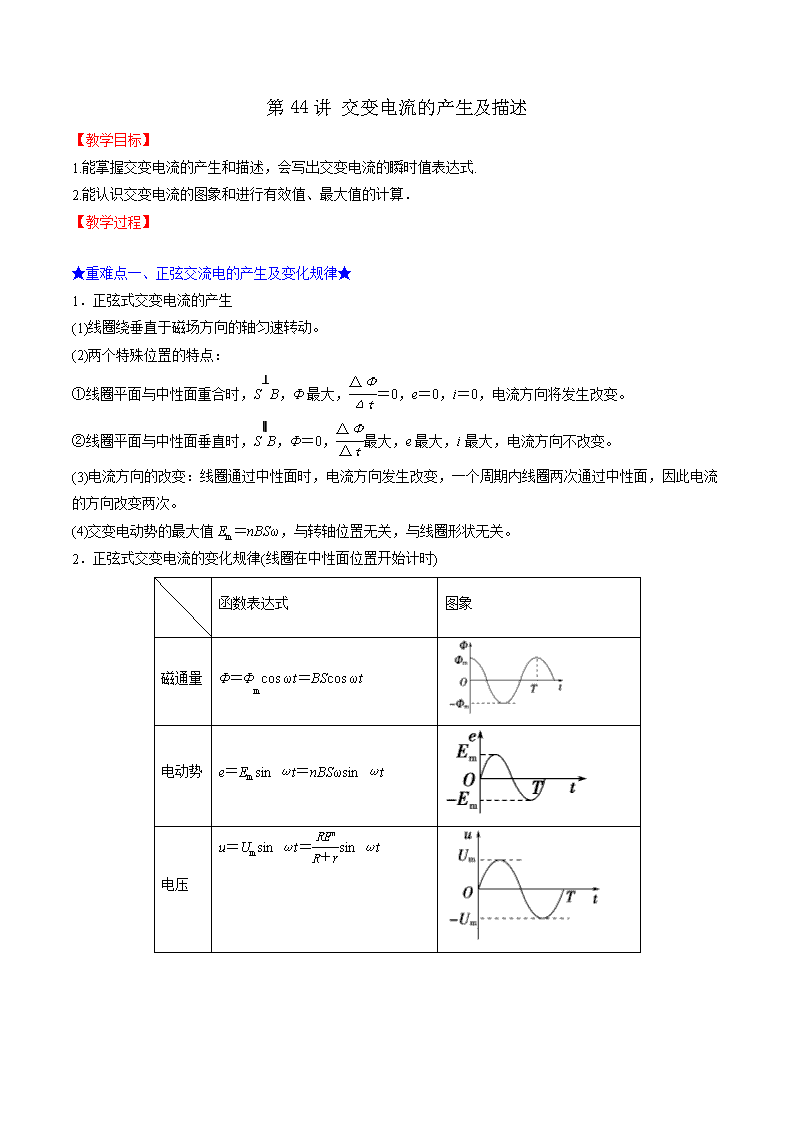
第44讲 交变电流的产生及描述 ‎【教学目标】‎ ‎1.能掌握交变电流的产生和描述，会写出交变电流的瞬时值表达式.‎ ‎2.能认识交变电流的图象和进行有效值、最大值的计算．‎ ‎【教学过程】‎ ‎ ‎ ‎★重难点一、正弦交流电的产生及变化规律★‎ ‎1．正弦式交变电流的产生 ‎(1)线圈绕垂直于磁场方向的轴匀速转动。‎ ‎(2)两个特殊位置的特点：‎ ‎①线圈平面与中性面重合时，S⊥B，Φ最大，＝0，e＝0，i＝0，电流方向将发生改变。‎ ‎②线圈平面与中性面垂直时，S∥B，Φ＝0，最大，e最大，i最大，电流方向不改变。‎ ‎(3)电流方向的改变：线圈通过中性面时，电流方向发生改变，一个周期内线圈两次通过中性面，因此电流的方向改变两次。‎ ‎(4)交变电动势的最大值Em＝nBSω，与转轴位置无关，与线圈形状无关。‎ ‎2．正弦式交变电流的变化规律(线圈在中性面位置开始计时)‎ 函数表达式 图象 磁通量 Φ＝Φmcos ωt＝BScos ωt 电动势 e＝Emsin ωt＝nBSωsin ωt 电压 u＝Umsin ωt＝sin ωt 电流 i＝Imsin ωt＝sin ωt ‎3.解决交变电流图象问题的三点注意 ‎（1）只有当线圈从中性面位置开始计时，电流的瞬时值表达式才是正弦形式，其变化规律与线圈的形状及转动轴处于线圈平面内的位置无关。‎ ‎（2）注意峰值公式Em＝nBSω中的S为有效面积。‎ ‎（3）在解决有关交变电流的图象问题时，应先把交变电流的图象与线圈的转动位置对应起来，再根据特殊位置求特征解。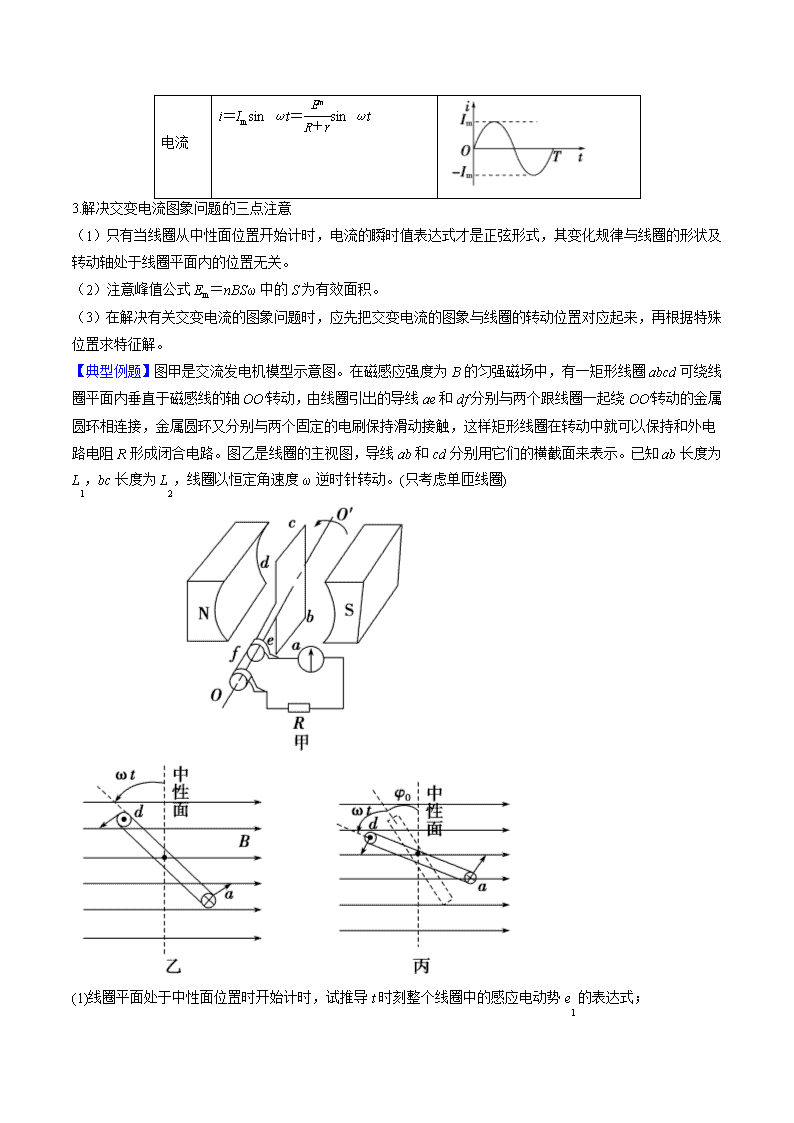‎ ‎【典型例题】图甲是交流发电机模型示意图。在磁感应强度为B的匀强磁场中，有一矩形线圈abcd可绕线圈平面内垂直于磁感线的轴OO′转动，由线圈引出的导线ae和df分别与两个跟线圈一起绕OO′转动的金属圆环相连接，金属圆环又分别与两个固定的电刷保持滑动接触，这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路。图乙是线圈的主视图，导线ab和cd分别用它们的横截面来表示。已知ab长度为L1，bc长度为L2，线圈以恒定角速度ω逆时针转动。(只考虑单匝线圈)‎ ‎(1)线圈平面处于中性面位置时开始计时，试推导t时刻整个线圈中的感应电动势e1的表达式；‎ ‎(2)线圈平面处于与中性面成φ0夹角位置时开始计时，如图丙所示，试写出t时刻整个线圈中的感应电动势e2的表达式。‎ ‎【答案】　(1)e1＝BL1L2ωsin ωt ‎(2)e2＝BL1L2ωsin(ωt＋φ0)‎ ‎【解析】　(1)矩形线圈abcd转动过程中，只有ab和cd切割磁感线，设ab和cd的转动速度为v，则 v＝ω·①‎ 在t时刻，导线ab和cd因切割磁感线而产生的感应电动势均为 E1＝BL1vy②‎ 由图可知vy＝vsin ωt③‎ 则整个线圈的感应电动势为e1＝2E1＝BL1L2ωsin ωt④‎ ‎(2)当线圈由图丙位置开始运动时，在t时刻整个线圈的感应电动势为e2＝BL1L2ωsin(ωt＋φ0)。‎ ‎★重难点二、有效值的理解与计算★‎ 对交变电流有效值的理解 ‎1．交变电流的有效值是根据电流的热效应(电流通过电阻生热)进行定义的，所以进行有效值计算时，要紧扣电流通过电阻生热(或热功率)进行计算。注意“三同”即“相同电阻”上，“相同时间”内产生“相同热量”。计算时“相同时间”至少要取一个周期的时间。‎ ‎2．在交流电路中，电压表、电流表、功率表等电工仪表的示数均为交变电流的有效值。在没有具体说明的情况下，所给出的交变电流的电压、电流及电功率指的都是有效值。‎ ‎3．非正弦式交变电流的有效值，应按有效值的定义计算。‎ ‎4．几种典型的电流及其有效值 名称 电流(电压)图象 有效值 正弦式交变电流 I＝ U＝ 正弦式半波脉冲电流 I＝ U＝ 正弦单向脉冲电流 I＝ U＝ 矩形脉冲电流 I＝ Im U＝ Um 非对称性交变电流 I＝ U＝ ‎4.计算交变电流有效值的方法 ‎(1)计算有效值时要根据电流的热效应，抓住“三同”：“相同时间”内“相同电阻”上产生“相同热量”列式求解。‎ ‎(2)分段计算电热求和得出一个周期内产生的总热量。‎ ‎(3)利用两类公式Q＝I2Rt和Q＝t可分别求得电流有效值和电压有效值。‎ ‎(4)若图象部分是正弦(或余弦)交流电，其中的(但必须是从零至最大值或从最大值至零)和周期部分可直接应用正弦式交变电流有效值与最大值间的关系I＝Im/、U＝Um/求解。‎ ‎【特别提醒】‎ ‎　计算交变电流有效值的方法 ‎1.要取一个周期的时间计算电热。‎ ‎2.分段处理：曲线为正弦的部分用I＝代替，不随时间变化的恒定的部分，有效值即为瞬时值。‎ ‎【典型例题】家用电子调光灯的调光功能是用电子线路将输入的正弦交流电压的波形截去一部分来实现的，由截去部分的多少来调节电压，从而实现灯光的可调，比过去用变压器调压方便且体积小。某电子调光灯经调整后电压波形如图所示，求灯泡两端的电压的有效值。‎ ‎【答案】 ‎【解析】从ut图像看出，每个周期的前半周期是正弦图形，其有效值为U1＝；后半周期电压为零。根据有效值的定义，T＝·＋0，解得U＝。‎ ‎★重难点三、交变电流“四值”的比较★‎ ‎1、交变电流的瞬时值、峰值、有效值和平均值的比较 物理量 物理含义 重要关系 应用情况及说明 瞬时值 交变电流某一时刻的值 e＝Emsin ωt，‎ u＝Umsin ωt，‎ i＝Imsin ωt 计算线圈某时刻的受力情况 最大值 最大的瞬时值 Em＝nBSω，‎ Em＝nΦmω，‎ Im＝ 当考虑某些电学元件(电容器、晶体管等)的击穿电压时，指的是交变电压的最大值 有效值 根据电流的热效应(电流通过电阻产生的热)进行定义 对正弦、余弦式交变电流 E＝，U＝，‎ I＝ ‎(1)通常所说的交变电流的电压、电流强度，交流电表的读数，保险丝的熔断电流值，电器设备铭牌上所标的电压、电流值都是指交变电流的有效值 ‎(2)计算与电流的热效应有关的量(如电功、电功率、电热等)用有效值 平均值 交变电流图象中图线与t轴所围成的面积与时间的比值 E＝BL，‎ E＝n，‎ I＝ 计算通过电路截面的电荷量 ‎2、书写交变电流瞬时值表达式的基本思路 ‎（1）求出角速度ω，ω＝＝2πf。‎ ‎（2）确定正弦式交变电流的峰值，根据已知图象读出或由公式Em＝nBSω求出相应峰值。‎ ‎（3）明确线圈的初始位置，找出对应的函数关系式。‎ ‎①若线圈从中性面位置开始转动，则i t图象为正弦函数图象，函数式为i＝Imsin ωt；‎ ‎②若线圈从垂直中性面位置开始转动，则i t图象为余弦函数图象，函数式为i＝Imcos ωt。‎ ‎【典型例题】如图所示，线圈abcd的面积是0.05 m2，共100匝，线圈电阻为1 Ω，外接电阻R＝9 Ω，匀强磁场的磁感应强度B＝ T，当线圈以300 r/min的转速匀速旋转时。问：‎ ‎(1)若从线圈处于中性面开始计时，写出线圈中感应电动势的瞬时值表达式；‎ ‎(2)线圈转过 s时电动势的瞬时值多大？‎ ‎(3)电路中，电压表和电流表的示数各是多少？‎ ‎(4)从中性面开始计时，经 s通过电阻R的电荷量是多少？‎ ‎【答案】(1)e＝50sin 10πt(V)　(2)43.3 V (3)31.86 V　3.54 A　(4) C ‎【解析】(1)e＝Emsin ωt＝nBS·2πfsin(2πft)＝100××0.05×2π×sinV＝50sin 10πt V ‎(2)当t＝ s时，e＝50sinV≈43.3 V ‎(3)电动势的有效值为E＝＝ V≈35.4 V 电流表示数I＝＝ A＝3.54 A 电压表示数U＝IR＝3.54×9 V＝31.86 V ‎(4) s内线圈转过的角度θ＝ωt＝×2π×＝ 该过程中，ΔΦ＝BS－BScos θ＝BS 由I＝，I＝，E＝ 得q＝＝＝ C＝ C