2021高考物理二轮复习专题四电路和电磁感应第12讲电磁感应课件 54页

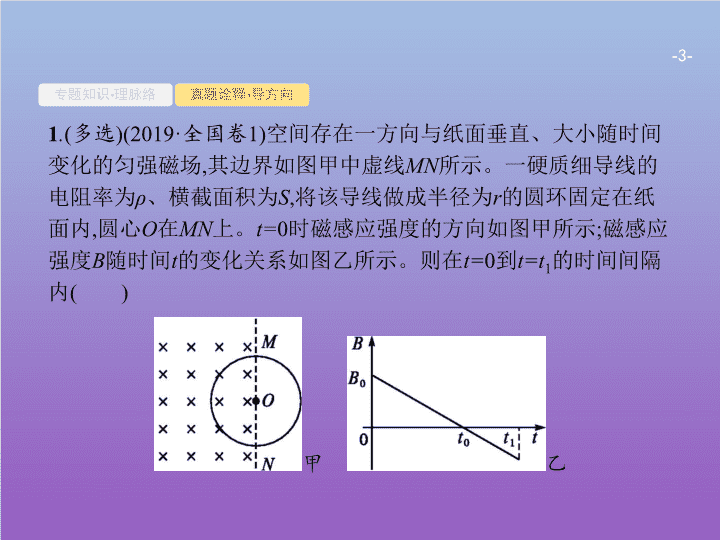
第 12 讲 　 电磁感应 - 2 - 专题知识 • 理脉络 真题诠释 • 导方向 - 3 - 专题知识 • 理脉络 真题诠释 • 导方向 1 . ( 多选 )(2019· 全国卷 1) 空间存在一方向与纸面垂直、大小随时间变化的匀强磁场 , 其边界如图甲中虚线 MN 所示。一硬质细导线的电阻率为 ρ 、横截面积为 S , 将该导线做成半径为 r 的圆环固定在纸面内 , 圆心 O 在 MN 上。 t= 0 时磁感应强度的方向如图甲所示 ; 磁感应强度 B 随时间 t 的变化关系如图乙所示。则在 t= 0 到 t=t 1 的时间间隔内 ( 　　 ) - 4 - 专题知识 • 理脉络 真题诠释 • 导方向 A. 圆环所受安培力的方向始终不变 B. 圆环中的感应电流始终沿顺时针方向 答案 : BC 　 解析 : 根据楞次定律可知 , 圆环中的感应电流始终沿顺时针方向 ,B 正确。从 0 时刻到 t 1 时刻 , 电流方向未变 , 磁场方向改变 , 根据左手定则 , 安培力方向必定改变 ,A 错误。根据法拉第电磁感应定律 , - 5 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 法拉第电磁感应定律 , 闭合电路欧姆定律。 能力要求 本题是电磁感应与电路相结合的综合题 , 根据题意应用楞次定律、左手定则、电磁感应定律、电阻定律与欧姆定律即可解题。 - 6 - 专题知识 • 理脉络 真题诠释 • 导方向 2 . ( 多选 )(2018· 全国卷 3) 如图甲所示 , 在同一平面内固定有一长直导线 PQ 和一导线框 R , R 在 PQ 的右侧。导线 PQ 中通有正弦式交变电流 i , i 的变化如图乙所示 , 规定从 Q 到 P 为电流正方向。导线框 R 中的感应电动势 ( 　　 ) D. 在 t=T 时最大 , 且沿顺时针 方向 AC - 7 - 专题知识 • 理脉络 真题诠释 • 导方向 解析 : PQ 中的电流在导线框 R 中产生变化的磁场 , 所以线框 R 中的 磁 增强 , 感应电流的磁场方向垂直纸面向里 , 感应电动势为顺时针方向 ,C 选项正确 ; 在 T 时刻 , 线框 R 中的磁场从垂直纸面向外减弱变为垂直纸面向里增强 , 感应电流的磁场方向垂直纸面向外 , 感应电动势为逆时针方向 ,D 选项错误。 - 8 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 电磁感应图像。 能力要求 据右手螺旋定则得出直导线周围的磁场方向 , 结合交变电流电流大小的变化 , 根据楞次定律判断电势的高低。 - 9 - 专题知识 • 理脉络 真题诠释 • 导方向 3 . (2019· 天津卷 ) 如图所示 , 固定在水平面上间距为 l 的两条平行光滑金属导轨 , 垂直于导轨放置的两根金属棒 MN 和 PQ 长度也为 l 、电阻均为 R , 两棒与导轨始终接触良好。 MN 两端通过开关 S 与电阻为 R 的单匝金属线圈相连 , 线圈内存在竖直向下均匀增加的磁场 , 磁通量变化率为常量 k 。图中虚线右侧有垂直于导轨平面向下的匀强磁场 , 磁感应强度大小为 B 。 PQ 的质量为 m , 金属导轨足够长、电阻忽略不计。 - 10 - 专题知识 • 理脉络 真题诠释 • 导方向 (1) 闭合 S, 若使 PQ 保持静止 , 需在其上加多大的水平恒力 F , 并指出其方向 ; (2) 断开 S, PQ 在上述恒力作用下 , 由静止开始到速度大小为 v 的加速过程中流过 PQ 的电荷量为 q , 求该过程安培力做的功 W 。 - 11 - 专题知识 • 理脉络 真题诠释 • 导方向 解析 : (1) 设线圈中的感应电动势为 E , 设 PQ 受到的安培力为 F 安 , 有 F 安 =BI PQ l ⑤ 保持 PQ 静止 , 由受力平衡 , 有 F=F 安 ⑥ 方向水平向右 。 - 12 - 专题知识 • 理脉络 真题诠释 • 导方向 (2) 设 PQ 由静止开始到速度大小为 v 的加速过程中 , PQ 运动的位移为 x , 所用时间为 Δ t , 回路中的磁通量变化为 Δ Φ , 平均感应电动势为 - 13 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 法拉第电磁感应定律 , 电磁感应中的能量问题。 能力要求 分析解答第 (2) 问时注意 分析功能 关系 , 求出安培力做功。 - 14 - 专题知识 • 理脉络 真题诠释 • 导方向 4 . (2018· 天津卷 ) 真空管道超高速列车的动力系统是一种将电能直接转换成平动动能的装置。图甲是某种动力系统的简化模型 , 图中粗实线表示固定在水平面上间距为 l 的两条平行光滑金属导轨 , 电阻忽略不计。 ab 和 cd 是两根与导轨垂直、长度均为 l 、电阻均为 R 的金属棒 , 通过绝缘材料固定在列车底部 , 并与导轨良好接触 , 其间距也为 l , 列车的总质量为 m 。列车启动前 , ab 、 cd 处于磁感应强度为 B 的匀强磁场中 , 磁场方向垂直于导轨平面向下 , 如图甲所示。为使列车启动 , 需在 M 、 N 间连接电动势为 E 的直流电源 , 电源内阻及导线电阻忽略不计。列车启动后电源自动关闭。 - 15 - 专题知识 • 理脉络 真题诠释 • 导方向 甲 乙 (1) 要使列车向右运行 , 启动时图甲中 M 、 N 哪个接电源正极 , 并简要说明理由 ; (2) 求刚接通电源时列车加速度 a 的大小 ; (3) 列车减速时 , 需在前方设置如图乙所示的一系列磁感应强度为 B 的匀强磁场区域 , 磁场宽度和相邻磁场间距均大于 l 。若某时刻列车的速度为 v 0 , 此时 ab 、 cd 均在无磁场区域 , 试讨论 : 要使列车停下来 , 前方至少需要多少块这样的有界磁场 ? - 16 - 专题知识 • 理脉络 真题诠释 • 导方向 解析 : (1) M 接电源正极。列车要向右运动 , 安培力方向应向右。根据左手定则 , 接通电源后 , 金属棒中电流方向由 a 到 b 、由 c 到 d , 故 M 接电源正极。 (2) 由题意 , 启动时 ab 、 cd 并联 , 设回路总电阻为 R 总 , 设两根金属棒所受安培力之和为 F , 有 F=IlB ③ 根据牛顿第二定律有 F=ma ④ - 17 - 专题知识 • 理脉络 真题诠释 • 导方向 (3) 设列车减速时 , cd 进入磁场后经 Δ t 时间 ab 恰好进入磁场 , 此过程中穿过两金属棒与导轨所围回路的磁通量的变化为 Δ Φ , 平均感应电动势为 E 1 , 由法拉第电磁感应定律有 设 cd 受到的平均安培力为 F' , 有 F'=I'lB ⑨ 以向右为正方向 , 设 Δ t 时间内 cd 受安培力冲量为 I 冲 , 有 I 冲 =-F' Δ t ⑩ 同理可知 , 回路出磁场时 ab 受安培力冲量仍为上述值 , 设回路进出 - 18 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 电磁感应 , 动量定理 , 牛顿运动定律。 能力要求 分析解答第 (3) 问的难点在于找出列车通过相同有界磁场过程动量变化量是相同的。 - 19 - 突破点一 突破点二 突破点三 突破点四 楞次定律与电磁感应定律的应用 考查方向 常以选择题形式考查。 突破方略 1 . 楞次定律中 “ 阻碍 ” 的主要表现形式 (1) 阻碍原磁通量的变化 ——“ 增反减同 ”; (2) 阻碍相对运动 ——“ 来拒去留 ”; (3) 使线圈面积有扩大或缩小的趋势 ——“ 增缩减扩 ”; (4) 阻碍原电流的变化 ( 自感现象 )——“ 增反减同 ”; (5) 感应电流产生的 “ 结果 ” 阻碍引起感应电流的 “ 原因 ” 。 - 20 - 突破点一 突破点二 突破点三 突破点四 2 . 求感应电动势大小的五种 类型 3 . 电磁感应现象中的电源与电路 (1) 产生感应电动势的那部分导体相当于电源。 (2) 在电源内部电流由负极流向正极。 (3) 电源两端的电压为路端电压。 - 21 - 突破点一 突破点二 突破点三 突破点四 模型构建 【例 1 】 ( 多选 )(2019· 湖南常德期末 ) 图甲为兴趣小组制作的无线充电装置中的受电线圈示意图 , 已知线圈匝数 n= 100 、电阻 r= 1 Ω 、横截面积 S= 1 . 5×10 - 3 m 2 , 外接电阻 R= 7 Ω 。线圈处在平行于线圈轴线的匀强磁场中 , 磁场的磁感应强度随时间变化如图乙所示 , 则 ( 　　 ) - 22 - 突破点一 突破点二 突破点三 突破点四 A. 在 t= 0 . 01 s 时通过 R 的电流发生改变 B. 在 t= 0 . 01 s 时线圈中的感应电动势 E= 0 . 6 V C. 在 0 ~ 0 . 02 s 内通过电阻 R 的电荷量 q= 1 . 5×10 - 3 C D. 在 0 . 02 ~ 0 . 03 s 内 R 产生的焦耳热为 Q= 1 . 8×10 - 3 J 答案 : BC 　 - 23 - 突破点一 突破点二 突破点三 突破点四 解析 : 根据楞次定律可知 , 在 0 ~ 0 . 01 s 内电流方向和在 0.01~0.02 s 内电流方向相同 , 故 A 错误 ; 根据法拉第电磁感应定律可知 : 故 B 正确 ; 在 0 ~ 0 . 02 s 内 , 产生的感应电流为 电荷量为 q=It= 0 . 075×0 . 02 C=1.5×10 -3 C, 故 C 正确 ; - 24 - 突破点一 突破点二 突破点三 突破点四 在 0.02~0.03 s 内 , 产生的感应电动势 为 R 上产生的热量为 Q=I' 2 Rt= 0 . 15 2 ×7×0 . 01 J=1.575×10 -3 J, 故 D 错误。 - 25 - 突破点一 突破点二 突破点三 突破点四 迁移训练 1 .(2019· 天津河西一模 ) 如图所示 , 弹簧上端固定 , 下端悬挂一个磁铁。如果在磁铁下端的水平桌面上放一个固定的闭合线圈 , 并使磁极上下振动。磁铁在向下运动的过程中 , 说法正确的是 ( 　　 ) A . 线圈给磁铁的磁场力始终向上 B. 线圈给磁铁的磁场力先向上再向下 C. 线圈给磁铁的磁场力始终向下 D. 线圈给磁铁的磁场力先向下再向上 A 解析 : 根据楞次定律的 “ 来拒去留 ”, 则当磁铁在向下运动的过程中 , 线圈产生感应电流 , 形成感应磁场 , 从而阻碍磁铁的向下运动 , 则线圈给它的磁场力始终向上 , 故 A 正确 ,B 、 C 、 D 错误。 - 26 - 突破点三 突破点四 突破点一 突破点二 电磁感应中的图像问题 突破方略 1 . 磁场变化产生感应电动势或感应电流时一般由 B - t 图像或 Φ - t 图像 , 判断 I - t 或 E - t 关系。 (1) 注意正方向的规定。 (2) B - t 图像、 Φ - t 图像的斜率不变时 , E 、 I 大小方向不变 ; 反之电流、电动势恒定时 , B ( Φ ) 随时间均匀变化。 (3) 安培力大小与 B 、 I 、 l 有关 , 当 I 、 l 不变 , B 随时间均匀变化时安培力随时间均匀变化。 2 . 导体棒、线框切割磁感线时有效切割长度 : 导体首尾连线在垂直磁场、垂直切割速度方向上的投影长度。 - 27 - 突破点三 突破点四 突破点一 突破点二 模型构建 【例 2 】 ( 多选 )(2019· 湖北省武汉市调研 ) 如图甲所示 , 在足够长的光滑的斜面上放置着金属线框 , 垂直于斜面方向的匀强磁场的磁感应强度 B 随时间的变化规律如图乙所示 ( 规定垂直斜面向上为正方向 ) 。 t= 0 时刻将线框由静止释放 , 在线框下滑的过程中 , 下列说法正确的是 ( 　　 ) A. 线框中产生大小、方向周期性变化的电流 B. MN 边受到的安培力先减小后增大 C. 线框做匀加速直线运动 D. 线框中产生的热量等于其机械能的损失 BC - 28 - 突破点三 突破点四 突破点一 突破点二 解析 : 穿过线框的磁通量先向下减小 , 后向上增加 , 则根据楞次定律可知 , 感应电流方向不变 , 选项 A 错误 ; 因 B 的变化率不变 , 则感应电动势不变 , 感应电流不变 , 而 B 的大小先减小后增加 , 根据 F=BIl 可知 , MN 边受到的安培力先减小后增大 , 选项 B 正确 ; 因线框平行的两边电流等大反向 , 则整个线框受的安培力为零 , 则线框下滑的加速度不变 , 线框做匀加速直线运动 , 选项 C 正确 ; 因安培力对线框做功为零 , 斜面光滑 , 则线框的机械能守恒 , 选项 D 错误。 - 29 - 突破点三 突破点四 突破点一 突破点二 以题说法 解决两类图像问题的方法 (1) 图像选择问题 求解物理图像的选择类问题可用 “ 排除法 ”, 即排除与题目要求相违背的图像 , 留下正确图像 ; 也可用 “ 对照法 ”, 即按照题目要求画出正确的草图 , 再与选项对照 , 选出正确选项。解决此类问题的关键就是把握图像特点 、 分析相关 物理量的函数关系、 分析物理过程 的变化规律或关键物理状态。 - 30 - 突破点三 突破点四 突破点一 突破点二 (2) 图像 分析问题 在 定性分析物理 图像时 , 要明确图像中的横轴与纵轴所代表的物理量 , 要弄清图像的物理意义 , 借助有关的物理概念、公式、定理和定律作出 分析判断 ; 而对物理图像定量计算时 , 要搞清图像所揭示的物理规律或物理量间的函数关系 , 并要注意物理量的单位换算问题 , 要善于挖掘图像中的隐含条件 , 明确有关图线与坐标轴所包围的面积、图线在某位置的斜率 ( 或其绝对值 ) 、图线在纵轴和横轴上的截距所表示的物理意义。 - 31 - 突破点三 突破点四 突破点一 突破点二 迁移训练 2 . (2019· 天津期末 ) 如图甲所示 , 闭合矩形导线框 abcd 固定在匀强磁场中 , 磁场的方向与导线框所在平面垂直 , 磁感应强度 B 随时间的变化规律如图乙所示。规定垂直纸面向外为磁场的正方向 , 顺时针方向为感应电流的正方向 , 水平向右为安培力的正方向。关于线框中的感应电流 i 和 ad 边所受的安培力 F 随时间 t 变化的图像 , 下列选项正确的是 ( 　　 ) B - 32 - 突破点三 突破点四 突破点一 突破点二 解析 : 由图示 B - t 图像可知 ,0 ~ 1 s 时间内 , B 增大 , Φ 增大 , 由楞次定律可知 , 感应电流是顺时针的 , 为正值 ;1 ~ 2 s 磁通量不变 , 无感应电流 ;2~3 s, B 的方向垂直纸面向外 , B 减小 , Φ 减小 , 由楞次定律可知 , 感应电流沿逆时针方向 , 感应电流是负的 ;3 ~ 4 s 内 , B 的方向垂直纸面向里 , B 增大 , Φ 增大 , 由楞次定律可知 , 感应电流沿逆时针方向 , 感应电流是负的 , 故 A 错误 ,B 正确。由左手定则可知 , 在 0~1 s 内 , ad 受到的安培力方向水平向右 , 是正的 ;1 ~ 2 s 无感应电流 , 没有安培力 ;2~4 s 时间内 , 安培力水平向左 , 是负的 ; 由法拉第电磁感应定律可知 , 感应 I 、 L 不变 , B 均匀变化 , 则安培力 F 均匀变化 , 不是定值 , 故 C 、 D 错误。 - 33 - 突破点三 突破点四 突破点一 突破点二 电磁感应中的动力学与能量综合问题 考查方向 常以计算题或选择题形式考查。 突破方略 1 . 电磁感应与动力学综合题的解题策略 (1) 做好电路分析 , 明确电源与外电路 , 可画等效电路图。 (2) 做好受力分析 , 把握安培力的特点 , 安培力大小与导体棒速度有关 , 一般在牛顿第二定律方程里讨论 , v 的变化影响安培力大小 , 进而影响加速度大小 , 加速度的变化又会影响 v 的变化。 (3) 做好运动过程分析 : 注意导体棒进入磁场或离开磁场时的速度是否达到 “ 收尾速度 ” 。 - 34 - 突破点三 突破点四 突破点一 突破点二 2 . 电磁感应中能量的三种求解方法 (1) 利用克服安培力做功求解 : 电磁感应中产生的电能等于克服安培力所做的功。 (2) 利用能量守恒定律求解 : 若只有电能和机械能参与转化 , 则机械能的减少量等于产生的电能。 (3) 利用电路的相关公式 —— 电功公式或电热公式求解 : 若通过电阻的电流是恒定的或电流的有效值已知 , 则可直接利用电功公式或焦耳定律求解热量。 特别提醒 注意区分回路中某个元件的热量和回路总热量 , 不能混淆。 - 35 - 突破点三 突破点四 突破点一 突破点二 模型构建 【例 3 】 (2019· 河北保定质检 ) 如图所示 , 竖直平行光滑金属导轨间距为 l , 上端接阻值为 R 的电阻 , 下端接电源和开关 S, 电源电动势为 E , 内阻为 R , 整个装置处于垂直导轨平面的匀强磁场中。当开关闭合时 , 一质量为 m , 电阻也为 R 的金属棒恰好能静止在导轨上 , 金属棒与导轨一直保持良好接触 , 导轨足够长且不计电阻 , 重力加速度为 g 。 ( 1) 求匀强磁场的磁感应强度 ; (2) 断开开关后 , 金属棒开始运动 , 求金属棒最终的运动速度。 - 36 - 突破点三 突破点四 突破点一 突破点二 分析推理 (1) 当开关 S 闭合时 , 电路结构是怎样的 ? (2) 断开开关后 , 金属棒做什么运动 ? (1) 提示 : 如图所示 。 (2) 提示 : 先是做加速度 a 越来越小的加速直线运动 , 最终做匀速直线运动。 - 37 - 突破点三 突破点四 突破点一 突破点二 解析 : (1) 设金属棒中电流为 I , 匀强磁场的磁感应强度为 B 由于金属棒静止 , 则 mg=BIl ① 对于整个电路 , 由闭合电路的欧姆定律 E= 2 IR+IR ② 由左手定则可知磁感应强度 B 的方向垂直于导轨平面向里 。 - 38 - 突破点三 突破点四 突破点一 突破点二 (2) 金属棒最终做匀速直线运动 , 仍然处于平衡状态 , 棒中电流仍为 I , 设感应电动势为 E' , 再由欧姆定律得 : E'= 2 IR ③ 设金属棒最终的速度大小为 v , 由法拉第电磁感应定律得 : E'=Blv ④ - 39 - 突破点三 突破点四 突破点一 突破点二 以题说法 解题思路 分析 - 40 - 突破点三 突破点四 突破点一 突破点二 迁移训练 3 . (2019· 湖北四地七校联考 ) 如图所示 , 相距 l= 0 . 5 m 的平行导轨 MNS 、 PQT 处在磁感应强度 B= 0 . 4 T 的匀强磁场中 , 水平导轨处的磁场方向竖直向上 , 光滑倾斜导轨处的磁场方向垂直于导轨平面斜向下。质量均为 m= 40 g 、电阻均为 R= 0 . 1 Ω 的导体棒 ab 、 cd 均垂直放置于导轨上 , 并与导轨接触良好 , 导轨电阻不计。 - 41 - 突破点三 突破点四 突破点一 突破点二 质量为 m C = 200 g 的物体 C, 用绝缘细线绕过光滑的定滑轮分别与导体棒 ab 、 cd 相连接。细线沿导轨中心线且在导轨平面内 , 细线及滑轮质量不计。已知倾斜导轨与水平面的夹角 θ = 37 ° , 水平导轨与 ab 棒间的动摩擦因数 μ = 0 . 4 。重力加速度 g 取 10 m/s 2 , 水平导轨足够长 , 导体棒 cd 运动中始终不离开倾斜导轨。物体 C 由静止释放 , 当它达到最大速度时下落高度 h= 1 m, 试求这一运动过程中 :(sin 37 ° = 0 . 6,cos 37 ° = 0 . 8) (1) 物体 C 能达到的最大速度 v m 是多少 ? (2) 系统产生的内能是多少 ? (3) 连接 cd 棒的细线对 cd 棒做的功是多少 ? - 42 - 突破点三 突破点四 突破点一 突破点二 答案 : (1)2 m/s 　 (2)1.2 J 　 (3)0.84 J 解析 : (1)C 达到最大速度 v m 时 , 由法拉第电磁感应定律得 , 回路的感应电动势为 E= 2 Blv m ① 导体棒 ab 、 cd 受到的安培力为 F=BIl ③ 对物体 C 受力分析可知 , m C g=T 线 = μ mg+ 2 F+mg sin 37 ° ④ 联立 ①②③④ 式得 v m =2 m/s 。 ⑤ (2) 设系统在该过程中产生的内能为 E 1 , 由能量守恒定律得 : 联立 ⑤⑥ 式 , 并代入数据解得 E 1 = 1 . 2 J 。 ⑦ - 43 - 突破点三 突破点四 突破点一 突破点二 (3) 导体棒 cd 的受力分析如图所示 , 运动过程中系统由于摩擦产生的内能 E 2 = μ mgh= 0 . 16 J 结合第 (2) 问的计算结果知 , 这一过程电流产生的内能 E 3 =E 1 -E 2 = 1 . 04 J 又因为 ab 棒、 cd 棒的电阻相等 , 故电流通过 cd 棒产生的内能 E 4 = 0 . 52 J ⑧ 对导体棒 cd , 设这一过程中细线对其做的功为 W , 克服安培力做的功大小是 W A , 则由动能定理得 : - 44 - 突破点三 突破点四 突破点一 突破点二 电磁感应与动量、能量综合问题 考查方向 常以计算题或选择题形式考查。 突破方略 1 . 应用动量定理可以由动量变化来求解变力的冲量。如在导体棒做非匀变速运动的问题中 , 应用动量定理可以解决牛顿运动定律不易 解答的 问题。 2 . 在相互平行的水平轨道间的双导体棒做切割磁感线运动时 , 由于这两根导体棒所受的安培力等大反向 , 合外力为零 , 若不受其他外力 , 两导体棒的总动量守恒 , 解决此类问题往往要应用动量守恒定律。 - 45 - 突破点三 突破点四 突破点一 突破点二 模型构建 【例 4 】 如图所示 , 两根质量均为 m= 2 kg 的金属棒垂直放在光滑的水平导轨上 , 左右两部分导轨间距之比为 1 ∶ 2, 导轨间有大小相等但左、右两部分方向相反的匀强磁场 , 两棒电阻与棒长成正比 , 不计导轨电阻。现用 250 N 的水平拉力 F 向右拉 CD 棒 , CD 棒运动 s= 0 . 5 m 时其上产生的焦耳热为 Q 2 = 30 J, 此时两棒速率之比为 v A ∶ v C = 1 ∶ 2, 现立即撤去拉力 F , 设导轨足够长且两棒始终在不同磁场中运动 , 求 : - 46 - 突破点三 突破点四 突破点一 突破点二 (1) 在 CD 棒运动 0 . 5 m 的过程中 , AB 棒上产生的热量 ; (2) 撤去拉力 F 瞬间 , 两棒的速度大小 v A 和 v C ; (3) 撤去拉力 F 后 , 两棒最终匀速运动的速度大小 v A ' 和 v C ' 。 分析推理 (1) 在 CD 棒运动 0 . 5 m 的过程中 , 两棒中电流相同吗 ? (2) 撤去拉力 F 后 , 两棒最终匀速运动的速度大小 v A ' 和 v C ' 相等吗 ? (1) 提示 : 相同。 (2) 提示 : 不相等。 - 47 - 突破点三 突破点四 突破点一 突破点二 答案 : (1)15 J 　 (2)4 m/s 　 8 m/s 　 (3)6.4 m/s 　 3.2 m/s 解析 : (1) 设两棒的长度分别为 l 和 2 l , 所以电阻分别为 R 和 2 R , 由于电路中任何时刻电流均相等 , 根据焦耳定律 Q=I 2 Rt 可知 Q 1 ∶ Q 2 = 1 ∶ 2, 则 AB 棒上产生的热量 Q 1 = 15 J 。 (2) 根据能量守恒定律 , 又 v A ∶ v C = 1 ∶ 2, 联立以上两式并代入数据得 v A = 4 m/s, v C = 8 m/s 。 - 48 - 突破点三 突破点四 突破点一 突破点二 (3) 撤去拉力 F 后 , AB 棒继续向左做加速运动 , 而 CD 棒向右做减速运动 , 两棒最终匀速运动时电路中电流为零 , 即两棒切割磁感线产生的电动势大小相等 , 此时两棒的速度满足 BLv A '=B· 2 Lv C ' 即 v A '= 2 v C ' ( 不对过程进行分析 , 认为系统动量守恒是常见错误 ) 对两棒分别应用动量定理 , 规定水平向左为正方向 , 联立以上各式解得 v A '= 6 . 4 m/s, v C '= 3 . 2 m/s 。 - 49 - 突破点三 突破点四 突破点一 突破点二 以题说法 对于双导体棒运动的问题 , 通常是两棒与导轨构成一个闭合回路 , 当其中一棒在外力作用下获得一定速度时必然在磁场中切割磁感线 , 在该闭合电路中形成一定的感应电流 ; 另一根导体棒在磁场中通电时在安培力的作用下开始运动 , 一旦运动起来也将切割磁感线产生一定的感应电动势 , 对原来电流的变化起阻碍作用。 - 50 - 突破点三 突破点四 突破点一 突破点二 迁移训练 4 . (2019· 宁夏一中模拟 ) 如图所示 , 在绝缘水平面上的两物块 A 、 B 用劲度系数为 k 的水平绝缘轻质弹簧连接 , 物块 B 、 C 用跨过轻质定滑轮的绝缘轻绳连接 ,A 靠在竖直墙边 ,C 在倾角为 θ 的长斜面上 , 滑轮两侧的轻绳分别与水平面和斜面平行。 A 、 B 、 C 的质量分别是 m 、 2 m 、 2 m ,A 、 C 均不带电 ,B 带正电 , 滑轮左侧存在着水平向左的匀强电场 , 整个系统不计一切摩擦 ,B 与滑轮足够远。 B 所受的电场力大小为 6 mg sin θ , 开始时系统静止。现让 C 在沿斜面向下的拉力 F 作用下做加速度大小为 a 的匀加速直线运动 , 弹簧始终未超过弹性限度 , 重力加速度大小为 g 。 - 51 - 突破点三 突破点四 突破点一 突破点二 (1) 求弹簧的压缩长度 x 1 ; (2) 求 A 刚要离开墙壁时 C 的速度大小 v 1 及拉力 F 的大小 ; (3) 若 A 刚要离开墙壁时 , 撤去拉力 F , 同时电场力大小突然减为 2 mg sin θ , 方向不变 , 求在之后的运动过程中弹簧的最大弹性势能 E pm 。 - 52 - 突破点三 突破点四 突破点一 突破点二 解析 : (1) 开始时 , 弹簧处于压缩状态 对 C 受力平衡有 F T1 = 2 mg sin θ 对 B 受力平衡有 F T1 +kx 1 = 6 mg sin θ - 53 - 突破点三 突破点四 突破点一 突破点二 (2)A 刚要离开墙壁时墙壁对 A 的弹力为零 , 弹簧刚好不发生形变 ,B 与 C 相连做匀加速直线运动 , 根据牛顿第二定律 对 B 有 : F T2 - 6 mg sin θ = 2 ma 对 C 有 : F+ 2 mg sin θ -F T2 = 2 ma 解得 F= 4 m ( g sin θ +a ) 。 - 54 - 突破点三 突破点四 突破点一 突破点二 (3)A 离开墙壁后 ,A 、 B 、 C 系统的合外力为零 , 系统动量守恒 , 当三个物块的速度相等时 ( 设为 v 2 ), 弹簧弹性势能最大 , 有 (2 m+ 2 m ) v 1 = ( m+ 2 m+ 2 m ) v 2 根据能量守恒定律有