【物理】2020届一轮复习人教版专题四曲线运动问题的解法学案 5页

专题四：曲线运动问题的解法 ‎1．分解法 应用平行四边形定则(或三角形定则)，将矢量进行分解(如合速度分解为分速度)的方法．‎ 例1 如图所示，一辆汽车沿水平地面匀速行驶，通过跨过定滑轮的轻绳将一物体A竖直向上提起，在此过程中，物体A的运动情况是(　　)‎ A．加速上升，且加速度不断增大 B．加速上升，且加速度不断减小 C．减速上升，且加速度不断减小 D．匀速上升 解析　物体A的速率即为左段绳子上移的速率，而左段绳子上移的速率与右段绳子在沿绳方向的分速率是相等的．右段绳子实际上同时参与两个运动：沿绳方向拉长及绕定滑轮逆时针转动．将右段绳子与汽车相连的端点的运动速度v沿绳子方向和沿与绳子垂直的方向分解，如图所示，则沿绳方向的速率即为物体A的速率vA＝v1＝vsinθ，随着汽车的运动，θ增大，vA增大，故物体A应加速上升．θ角在0°～90°范围内增大，由正弦曲线形状可知vA的变化率减小，故物体A上升的加速度逐渐减小．‎ 答案　B 规律总结　‎ 解决“绳连”问题的具体方法可以概括为：绳端的速度是合速度，绳端的运动包含了两个分效果：沿绳方向的分运动(伸长或缩短)，垂直于绳方向的分运动(转动)，故可以将绳端的速度分解为沿绳(伸长或收缩)方向的分速度和垂直于绳方向的分速度．另外，同一条绳子的两端沿绳方向的分速度大小相等．‎ ‎2．合成法 应用平行四边形定则(或三角形定则)，将分矢量进行合成(如分速度合成为合速度)的方法．‎ 例2玻璃板生产线上宽‎9 m的成型玻璃板以‎4 m/s的速度连续不断地向前运动，在切割工序处，金刚钻割刀的速度为‎8 m/s，为了使割下的玻璃都成规定尺寸的矩形，金刚钻割刀的轨道应如何控制？切割一次的时间多长？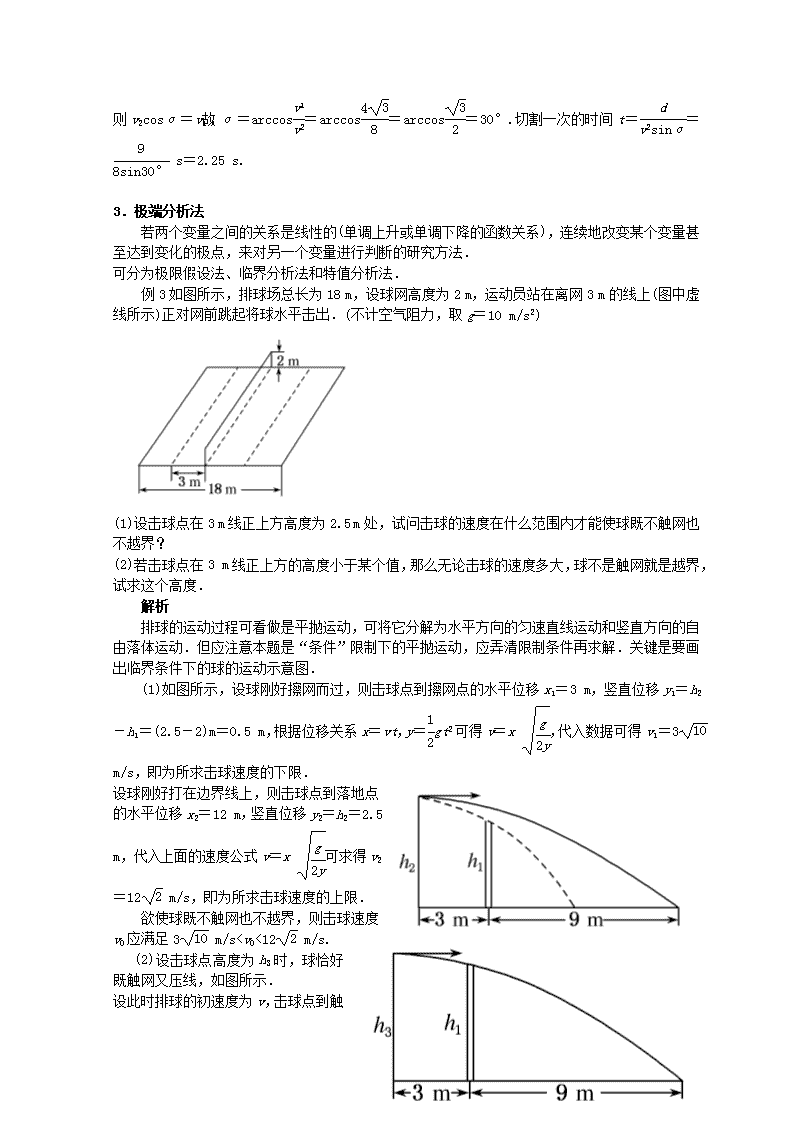‎ 解析　为了使割下的玻璃都成规定尺寸的矩形．金刚钻割刀沿玻璃板运动方向的分速度与玻璃板的速度大小应相等．将金刚钻割刀的速度沿玻璃板运动方向和垂直玻璃板运动方向分解，如图，设金刚钻割刀的速度方向与玻璃板运动方向成α角，以v1、v2‎ 分别表示玻璃板和金刚钻割刀的速度，则v2cosα＝v1，故α＝arccos＝arccos＝arccos＝30°.切割一次的时间t＝＝ s＝2.25 s.‎ ‎3．极端分析法 若两个变量之间的关系是线性的(单调上升或单调下降的函数关系)，连续地改变某个变量甚至达到变化的极点，来对另一个变量进行判断的研究方法．‎ 可分为极限假设法、临界分析法和特值分析法．‎ 例3如图所示，排球场总长为‎18 m，设球网高度为‎2 m，运动员站在离网‎3 m的线上(图中虚线所示)正对网前跳起将球水平击出．(不计空气阻力，取g＝‎10 m/s2)‎ ‎(1)设击球点在‎3 m线正上方高度为‎2.5 m处，试问击球的速度在什么范围内才能使球既不触网也不越界？‎ ‎(2)若击球点在‎3 m线正上方的高度小于某个值，那么无论击球的速度多大，球不是触网就是越界，试求这个高度．‎ 解析　‎ 排球的运动过程可看做是平抛运动，可将它分解为水平方向的匀速直线运动和竖直方向的自由落体运动．但应注意本题是“条件”限制下的平抛运动，应弄清限制条件再求解．关键是要画出临界条件下的球的运动示意图．‎ ‎(1)如图所示，设球刚好擦网而过，则击球点到擦网点的水平位移x1＝‎3 m，竖直位移y1＝h2－h1＝(2.5－2)m＝‎0.5 m，根据位移关系x＝vt，y＝gt2可得v＝x ，代入数据可得v1＝‎3 m/s，即为所求击球速度的下限．‎ 设球刚好打在边界线上，则击球点到落地点的水平位移x2＝‎12 m，竖直位移y2＝h2＝‎2.5 m，代入上面的速度公式v＝x 可求得v2＝‎12 m/s，即为所求击球速度的上限．‎ 欲使球既不触网也不越界，则击球速度v0应满足‎3 m/s