【物理】2018届一轮复习人教版运动的合成与分解教案 7页

‎ 运动的合成与分解 ‎【教学目标】‎ ‎1.掌握曲线运动的概念、特点及条件.‎ ‎2.掌握运动的合成与分解法则． ‎ ‎【教学过程】‎ ‎★重难点一、物体做曲线运动的条件与轨迹分析★‎ 曲线运动的特点 曲线运动的条件 内容 物体在某一点的速度沿曲线上该点的切线方向 物体所受合力的方向与它的速度方向不在同一直线上 深入理解 ‎①速度方向时刻在变化，所以曲线运动一定是变速运动 ‎②速度大小可以不变，相应的动能就不变，如匀速圆周运动 ‎③加速度可以是不变的，即物体做匀变速曲线运动，如平抛运动 ‎④加速度可以是变化的，即物体做非匀变速曲线运动，如匀速圆周运动 ‎①合力指向曲线的凹侧，所以合力与速度分居曲线两侧 ‎②合力可以是不变的，如平抛运动中物体的合力为重力，大小、方向都不变 ‎③合力可以是变化的，如匀速圆周运动中物体的合力为向心力，方向时刻在变化 ‎【特别提醒】‎ ‎1．合力方向与轨迹的关系 物体做曲线运动的轨迹一定夹在合力方向与速度方向之间，速度方向与轨迹相切，合力方向指向轨迹的“凹”侧。‎ ‎2．合力方向与速率变化的关系 ‎【典型例题】质点做曲线运动从A到B 速率逐渐增加，如图所示，有四位同学用示意图表示A到B的轨迹及速度方向和加速度的方向，其中正确的是(　　)‎ ‎【答案】D ‎★重难点二、运动的合成与分解的应用★‎ ‎1．合运动与分运动的关系 ‎(1)等时性：各个分运动与合运动总是同时开始，同时结束，经历时间相等(不同时的运动不能合成)。‎ ‎(2)等效性：各分运动叠加起来与合运动有相同的效果。‎ ‎(3)独立性：一个物体同时参与几个运动，其中的任何一个都会保持其运动性质不变，并不会受其他分运动的干扰。虽然各分运动互相独立，但是它们共同决定合运动的性质和轨迹。‎ ‎2．运动的合成与分解的运算法则 运动的合成与分解是指描述运动的各物理量，即位移、速度、加速度的合成与分解，由于它们均是矢量，故合成与分解都遵守平行四边形定则。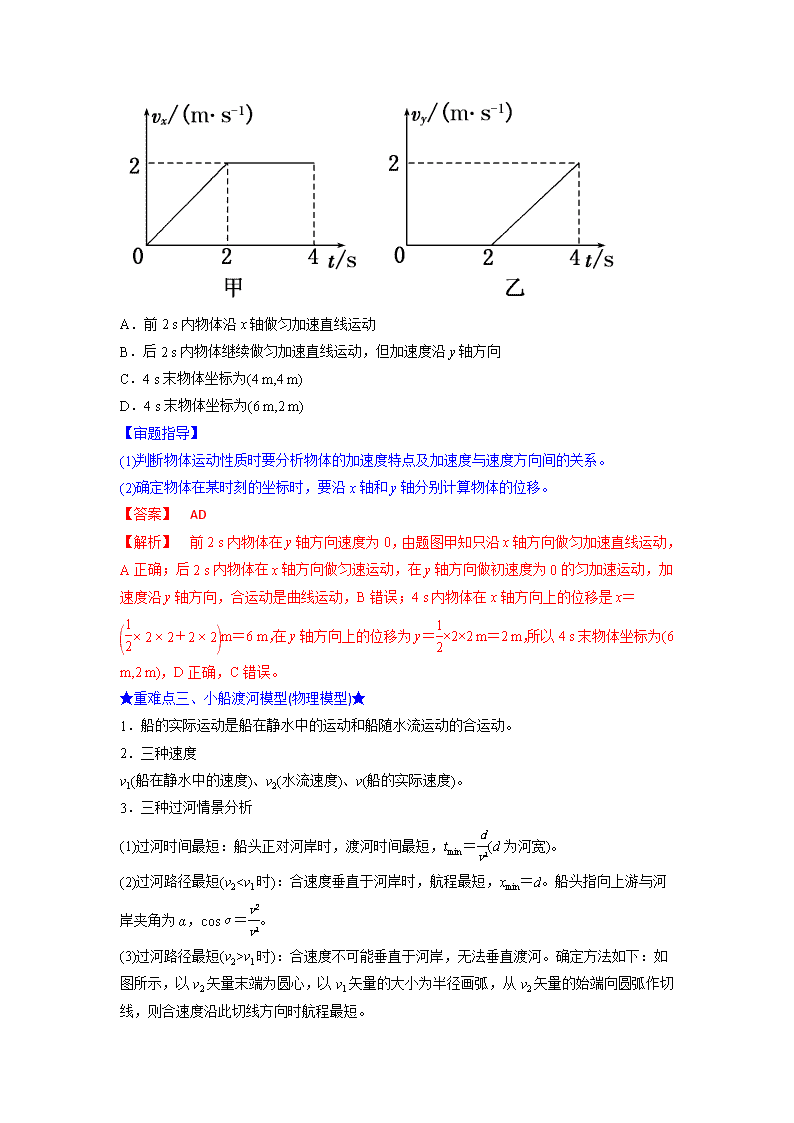‎ ‎3．合运动性质的判断 ‎【典型例题】(多选)在一光滑水平面内建立平面直角坐标系，一物体从t＝0时刻起，由坐标原点O(0,0)开始运动，其沿x轴和y轴方向运动的速度—时间图像如图甲、乙所示，下列说法中正确的是 (　　)‎ A．前2 s内物体沿x轴做匀加速直线运动 B．后2 s内物体继续做匀加速直线运动，但加速度沿y轴方向 C．4 s末物体坐标为(4 m,4 m)‎ D．4 s末物体坐标为(6 m,2 m)‎ ‎【审题指导】‎ ‎(1)判断物体运动性质时要分析物体的加速度特点及加速度与速度方向间的关系。‎ ‎(2)确定物体在某时刻的坐标时，要沿x轴和y轴分别计算物体的位移。‎ ‎【答案】　AD ‎【解析】　前2 s内物体在y轴方向速度为0，由题图甲知只沿x轴方向做匀加速直线运动，A正确；后2 s内物体在x轴方向做匀速运动，在y轴方向做初速度为0的匀加速运动，加速度沿y轴方向，合运动是曲线运动，B错误；4 s内物体在x轴方向上的位移是x＝m＝6 m，在y轴方向上的位移为y＝×2×2 m＝2 m，所以4 s末物体坐标为(6 m,2 m)，D正确，C错误。‎ ‎★重难点三、小船渡河模型(物理模型)★‎ ‎1．船的实际运动是船在静水中的运动和船随水流运动的合运动。‎ ‎2．三种速度 v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。‎ ‎3．三种过河情景分析 ‎(1)过河时间最短：船头正对河岸时，渡河时间最短，tmin＝(d为河宽)。‎ ‎(2)过河路径最短(v2v1时)：合速度不可能垂直于河岸，无法垂直渡河。确定方法如下：如图所示，以v2矢量末端为圆心，以v1矢量的大小为半径画弧，从v2矢量的始端向圆弧作切线，则合速度沿此切线方向时航程最短。‎ 由图可知cosα＝，‎ 最短航程s短＝＝d。‎ ‎4．小船渡河问题的分析思路 ‎【特别提醒】‎ 求解小船渡河问题的3点注意 ‎1.船的航行方向是船头指向，是分运动；船的运动方向是船的实际运动方向，是合运动，一般情况下与船头指向不一致。‎ ‎2.渡河时间只与船垂直于河岸方向的分速度有关，与水流速度无关。‎ ‎3.船渡河位移的最小值与v船和v水的大小关系有关，v船>v水时，河宽即为最小位移；v船vB B．vA