【物理】2020届一轮复习人教版跨滑轮绳连接物体系的牛顿第二定律教案 4页

跨滑轮绳连接物体系的牛顿第二定律 一、问题的缘起 A B ‎【例1】如图所示，物体A和B由跨过轻质滑轮的轻绳连接后竖直悬挂，然后由静止释放，已知A的质量为m、B的质量为M，且M＞m，不计一切摩擦，求A上升的加速度。‎ 本题常见两种解法，如下：‎ 解法一：设绳中张力为FT，则由牛顿第二定律，对A，有：FT－mg=maA，对B，有Mg－FT=MaB，其中：aA=aB，联立解得：。‎ 解法二：选A、B、轻绳系统为研究对象，由系统的牛顿第二定律，有：Mg－mg=(M+m)a，解得：。‎ ‎【质疑】按常规理解，第二种解法存在一些明显的问题：等式左边，两个重力方向均向下，按矢量合成规则，怎么能够相减？等式右边，aA、aB两个加速度方向相反，MaB和maA怎么能够相加？而且，真的选A、B、轻绳系统为研究对象，其受力还有滑轮对整体向上的弹力F，且系统的牛顿第二定律的方程应为：Mg+mg－F=Ma-ma。‎ ‎【解释】当然，我们可以认为，解法二的方程实际上是解法一两个方程联立得到的一个数学结论式，没有物理意义。可是，列解法二方程时，我们的解释往往是：我们研究的是A、B沿绳的运动——A、B沿绳运动的加速度相同，沿绳方向看，两个重力的方向相反，所以有：Mg－mg=(M+m)a。明显，这种理解是有物理意义的，那么，前面的质疑又如何回应？或者说这种理解是不科学、不严谨的?‎ 二、问题的解决 ‎1、曲线坐标系下物体运动的动力学 ‎·‎ O s 在上述问题中，我们可以在绳上取某个点为原点，规定从物体A经滑轮到物体B为该曲线的“正方向”，从而建立起一个描述物体运动位置的“曲线坐标系”。‎ 如果物体沿绳运动，则其沿绳运动的加速度即为自然坐标系下的切向加速度，由牛顿第二定律，有：；如果物体不沿绳运动，我们可以将物体运动分解到垂直绳和沿绳方向，物体沿绳方向的加速度可根据极坐标系等求出，沿绳方向仍然有动力学方程：。‎ ‎·‎ O mg Mg a s ‎2、跨滑轮绳连接物体系的牛顿第二定律 在前述例题中，若我们沿绳建立曲线坐标系，规定从A经滑轮到B为正方向，则分别对两物体列动力学方程，有：‎ 对A：‎ 对B：‎ 其中：aA=aB=a，‎ 前两式相加，得：Mg－mg=(M+m)a 此式即为A、B、轻绳系统在曲线坐标系下的牛顿第二定律方程，其理解就是：B均沿绳的运动——沿绳方向看，A、B沿绳运动的加速度相同，两个重力的方向相反，所以有：‎ Mg－mg=(M+m)a ‎【例2】如图所示，压力传感器能测量物体对其正压力的大小，现将质量分别为M、m的物块和小球通过轻绳固定，并跨过两个水平固定的定滑轮（滑轮光滑且较小），当小球在竖直面内左右摆动且高度相等时，物块始终没有离开水平放置的传感器．已知小球摆动偏离竖直方向的最大角度为θ，滑轮O到小球间细线长度为l，重力加速度为g，求：小球摆到最低点时，压力传感器示数为0，则M/m的大小．‎ ‎【解析】设小球在最低点速度为v，则由机械能守恒，有 ‎·‎ O’‎ Mg mg s 当小球运动到最低点时，沿绳方向建立如图所示曲线坐标系；此时，物块M沿绳的加速度为零，但小球m绕O点做圆周运动，因此有沿绳方向的加速度，则由系统的牛顿第二定律，有 解得：‎ 三、对物体系的牛顿第二定律的一个说明 物体系的牛顿第二定律的方程的得来，是先用隔离法分别对系统内各个物体列牛顿第二定律的方程，然后几个方程相加而得来，在相加过程中，我们做了一个“数学处理”——作用力和反作用力等大反向，“相加为零”。‎ 这个数学处理，从物理角度来说是不合适的，作用力和反作用力分别作用在系统内不同物体上，其效果是不能叠加的，因此“相加为零”是不合适的。从这个意义上讲，物体系的牛顿第二定律的方程是一个数学方程，不具有严谨的物理意义。很多学生很难理解物体系的牛顿第二定律，他们常常问的问题是：作用在A上的外力，如何能够在B上产生加速度？‎ A B 但是，这个数学方程用起来是方便的，因为该方程中没有内力，所以列出的方程简单。在用曲线坐标系处理跨滑轮绳连接物体系的运动时，绳中张力即是内力，且等大、反向，因此也没有出现在方程中。此时用物体系的牛顿第二定律还避免了滑轮弹力（其方向是垂直绳的）的引入，大大简化了方程和计算。‎ 四、应用示例 ‎【例3】如图‎·‎ O mg Mg a Ff s FN 所示，固定的粗糙斜面顶端有一个轻质滑轮，物体A和B由跨过滑轮的轻绳连接，然后由静止释放，已知斜面倾角为θ，A物体与斜面的动摩擦因数μ，A的质量为m、B的质量为M，且M＞m，轻绳足够长，求B下降的加速度。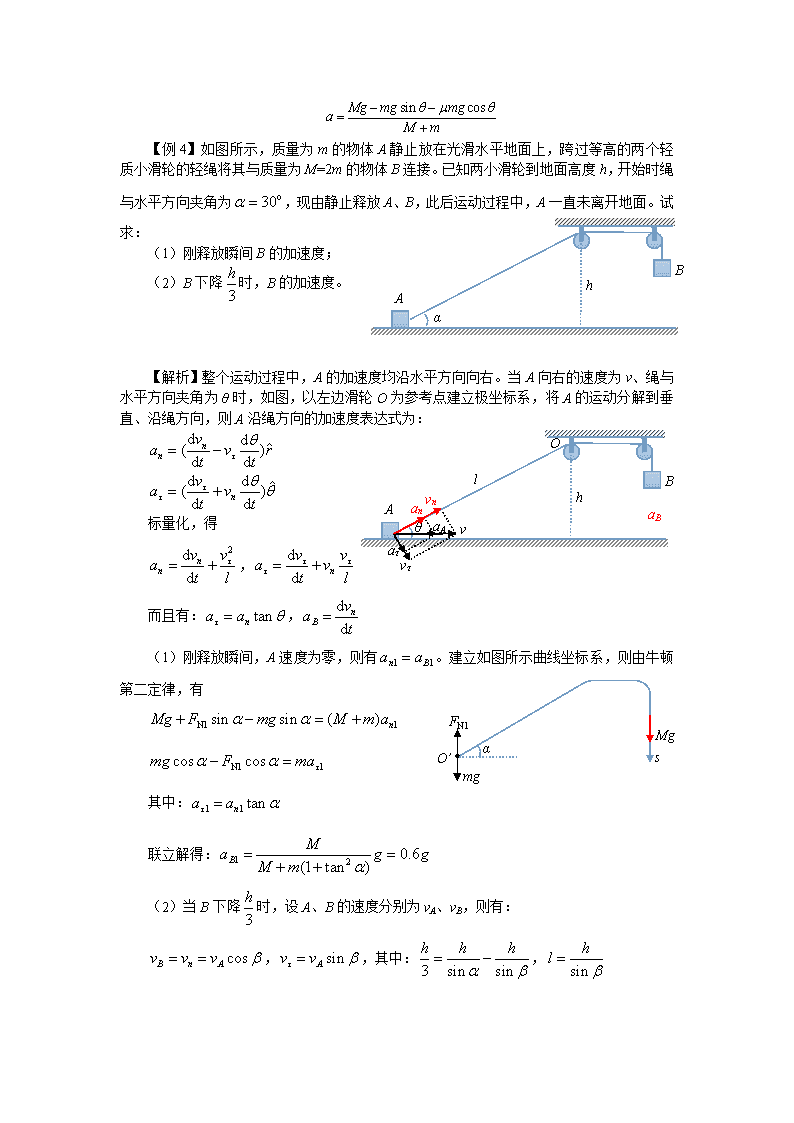‎ ‎【解析】如图，沿绳建立曲线坐标系，规定从A经滑轮到B为正方向，则对A、B、轻绳系统，由系统的牛顿第二定律，有 Mg－mgsinθ－μmgcosθ=(M+m)a 解得：‎ ‎【例4】如图A B h α 所示，质量为m的物体A静止放在光滑水平地面上，跨过等高的两个轻质小滑轮的轻绳将其与质量为M=2m的物体B连接。已知两小滑轮到地面高度h，开始时绳与水平方向夹角为，现由静止释放A、B，此后运动过程中，A一直未离开地面。试求：‎ ‎（1）刚释放瞬间B的加速度；‎ ‎（2）B下降时，B的加速度。‎ ‎【解析】整个运动过程中，A的加速度均沿水平方向向右。当A向右的速度为v、绳与水平方向夹角为θ时，如图，以左边滑轮O为参考点建立极坐标系，将A的运动分解到垂直、沿绳方向，则A沿绳方向的加速度表达式为：‎ A B h θ O v vn vτ l aτ an aB aA 标量化，得 ‎，‎ 而且有：，‎ ‎（1）刚‎·‎ O’‎ mg Mg s FN1‎ α 释放瞬间，A速度为零，则有。建立如图所示曲线坐标系，则由牛顿第二定律，有 其中：‎ 联立解得：‎ ‎（2）当B下降时，设A、B的速度分别为vA、vB，则有：‎ ‎，，其中：，‎ 此时，对A，有：，且，‎ Mg s ‎·‎ O’‎ mg FN2‎ β 建立如图所示曲线坐标系，则由牛顿第二定律，有 由机械能守恒，有 联立解得：‎