【物理】2019届一轮复习人教版第十三章第一单元光的传播几何光学教案 6页

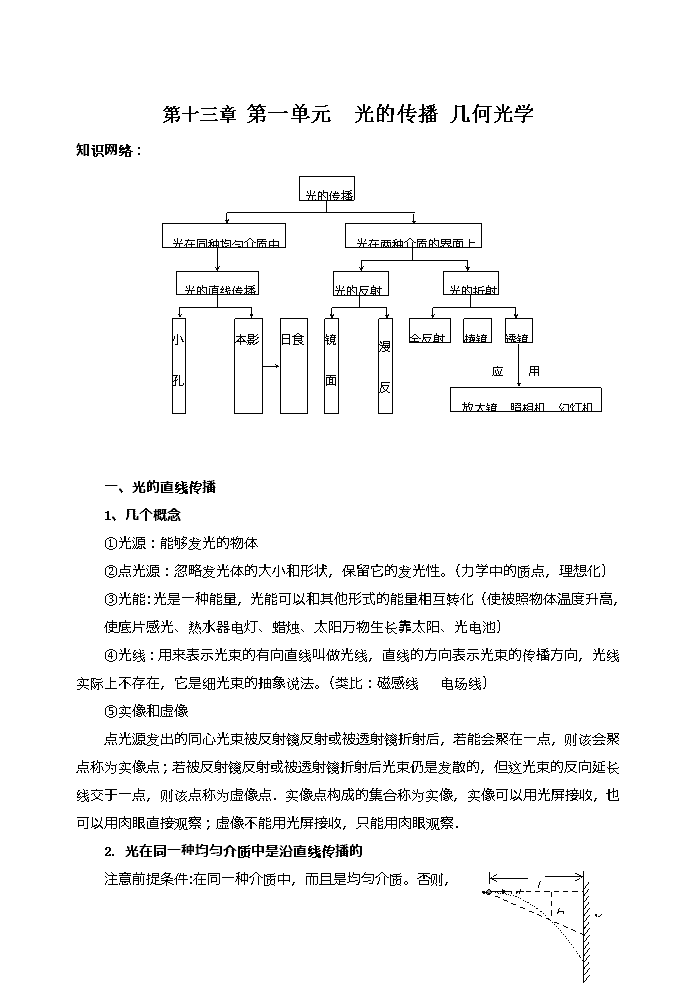
第十三章 第一单元 光的传播 几何光学 知识网络：‎ 应　　用 光的传播 光在同种均匀介质中 光在两种介质的界面上 光的直线传播 光的反射 光的折射 小孔成像 本影 半影 日食 月食 镜面反射 漫反射 全反射 棱镜 透镜 放大镜　照相机　幻灯机 一、光的直线传播 ‎ ‎1、几个概念 ‎①光源：能够发光的物体 ‎②点光源：忽略发光体的大小和形状，保留它的发光性。（力学中的质点，理想化）‎ ‎③光能：光是一种能量，光能可以和其他形式的能量相互转化（使被照物体温度升高，使底片感光、热水器电灯、蜡烛、太阳万物生长靠太阳、光电池）‎ ‎④光线：用来表示光束的有向直线叫做光线，直线的方向表示光束的传播方向，光线实际上不存在，它是细光束的抽象说法。（类比：磁感线 电场线）‎ ‎⑤实像和虚像 点光源发出的同心光束被反射镜反射或被透射镜折射后，若能会聚在一点，则该会聚点称为实像点；若被反射镜反射或被透射镜折射后光束仍是发散的，但这光束的反向延长线交于一点，则该点称为虚像点．实像点构成的集合称为实像，实像可以用光屏接收，也可以用肉眼直接观察；虚像不能用光屏接收，只能用肉眼观察．‎ ‎2．光在同一种均匀介质中是沿直线传播的 l S A h x vt 注意前提条件：在同一种介质中，而且是均匀介质。否则，可能发生偏折。如光从空气斜射入水中（不是同一种介质）；“海市蜃楼”现象（介质不均匀）。‎ 点评：光的直线传播是一个近似的规律。当障碍物或孔的尺寸和波长可以比拟或者比波长小时，将发生明显的衍射现象，光线将可能偏离原来的传播方向。‎ ‎【例1】如图所示，在A点有一个小球，紧靠小球的左方有一个点光源S。现将小球从A 点正对着竖直墙平抛出去，打到竖直墙之前，小球在点光源照射下的影子在墙上的运动是 A.匀速直线运动 B.自由落体运动 C.变加速直线运动 D.匀减速直线运动 解：小球抛出后做平抛运动，时间t后水平位移是vt，竖直位移是h=gt2，根据相似形知识可以由比例求得，因此影子在墙上的运动是匀速运动。‎ ‎【例2】某人身高1.8 m，沿一直线以2 m/s的速度前进，其正前方离地面5 m高处有一盏路灯，试求人的影子在水平地面上的移动速度。‎ 解析：如图所示，设人在时间t内由开始位置运动到G位置，人头部的影子由D点运动到C点。‎ G F E D C B A 三角形ABC∽FGC，有 因为三角形ACD∽AFE，所以有 由以上各式可以得到 即= 解得S影=3.125t 。‎ 可见影的速度为3.125m/s 。‎ 二、反射 平面镜成像 ‎1、反射定律 光射到两种介质的界面上后返回原介质时，其传播规律遵循反射定律．反射定律的基本内容包含如下三个要点：‎ ‎① 反射光线、法线、入射光线共面；‎ ‎② 反射光线与入射光线分居法线两侧；‎ ‎③ 反射角等于入射角，即　‎ ‎2．平面镜成像的特点——平面镜成的像是正立等大的虚像，像与物关于镜面对称 ‎3．光路图作法——根据成像的特点，在作光路图时，可以先画像，后补画光路图。‎ ‎4．充分利用光路可逆——在平面镜的计算和作图中要充分利用光路可逆。（眼睛在某点A通过平面镜所能看到的范围和在A点放一个点光源，该点光源发出的光经平面镜反射后照亮的范围是完全相同的。）‎ S S /‎ M N P Q ‎5．利用边缘光线作图确定范围 ‎【例3】 如图所示，画出人眼在S处通过平面镜可看到障碍物后地面的范围。‎ 解：先根据对称性作出人眼的像点S /，再根据光路可逆，设想S 处有一个点光源，它能通过平面镜照亮的范围就是人眼能通过平面镜看到的范围。图中画出了两条边缘光线。‎ ‎【例4】如图所示，用作图法确定人在镜前通过平面镜可看到AB完整像的范围。‎ 解：先根据对称性作出AB的像A/B/，分别作出A点、B点发出的光经平面镜反射后能射到的范围，再找到它们的公共区域（交集）。就是能看到完整像的范围。‎ 三、折射与全反射 ‎1．折射定律 (荷兰 斯涅尔)‎ i r 光射到两种介质的界面上后从第一种介质进入第二种介质时，其传播规律遵循折射定律．折射定律的基本内容包含如下三个要点：‎ ‎① 折射光线、法线、入射光线共面；‎ ‎② 折射光线与入射光线分居法线两侧；‎ ‎③ 入射角的正弦与折射角的正弦之比等于常数，即 折射定律的各种表达形式： (θ1为入、折射角中的较大者，C为全反射时的临界角。)‎ ‎④折射光路是可逆的。‎ ‎⑤n＞1‎ ‎⑥介质确定，n确定。（空气1.00028 水n＝1.33 酒精n＝1.6）（不以密度为标准）‎ ‎⑦光密介质和光疏介质——（1）与密度不同(2)相对性 （3）n大角小，n小角大 ‎2．全反射现象 ‎（1）现象：光从光密介质进入到光速介质中时，随着入射角的增加，折射光线远离法线，强度越来越弱，但是反射光线在远离法线的同时强度越来越强，当折射角达到90度时，折射光线认为全部消失，只剩下反射光线——全反射。‎ ‎（2）条件：①光从光密介质射向光疏介质；② 入射角达到临界角，即 ‎（3）临界角: 折射角为900（发生全发射）时对应的入射角,‎ α A B C D ‎【例5】 直角三棱镜的顶角α=15°， 棱镜材料的折射率n=1.5，一细束单色光如图所示垂直于左侧面射入，试用作图法求出该入射光第一次从棱镜中射出的光线。‎ 解：由n=1.5知临界角大于30°小于45°，边画边算可知该光线在射到A、B、C、D各点时的入射角依次是75°、60°、45°、30°，因此在A、B、C均发生全反射，到D点入射角才第一次小于临界角，所以才第一次有光线从棱镜射出。‎ ‎3．光导纤维，海市蜃楼和内窥镜 全反射的一个重要应用就是用于光导纤维（简称光纤）。光纤有内、外两层材料，其中内层是光密介质，外层是光疏介质。光在光纤中传播时，每次射到内、外两层材料的界面，都要求入射角大于临界角，从而发生全反射。这样使从一个端面入射的光，经过多次全反射能够没有损失地全部从另一个端面射出。‎ α ‎【例6】如图所示，一条长度为L=5.0m的光导纤维用折射率为n=的材料制成。一细束激光由其左端的中心点以α= 45°‎ 的入射角射入光导纤维内，经过一系列全反射后从右端射出。求：⑴该激光在光导纤维中的速度v是多大？⑵该激光在光导纤维中传输所经历的时间是多少？‎ 解：⑴由n=c/v可得v =2.1×108m/s ‎⑵由n=sinα/sinr可得光线从左端面射入后的折射角为30°，射到侧面时的入射角为60°，大于临界角45°，因此发生全反射，同理光线每次在侧面都将发生全反射，直到光线达到右端面。由三角关系可以求出光线在光纤中通过的总路程为s=2L/，因此该激光在光导纤维中传输所经历的时间是t=s/v=2.7×10-8s。‎ 四、棱镜和玻璃砖对光路的作用 ‎1．棱镜对光的偏折作用 一般所说的棱镜都是用光密介质制作的。入射光线经三棱镜两次折射后，射出方向与入射方向相比，向底边偏折，虚像向顶角偏移。‎ a b M ‎【例7】 如图所示，一细束红光和一细束蓝光平行射到同一个三棱镜上，经折射后交于光屏上的同一个点M，若用n1和n2分别表示三棱镜对红光和蓝光的折射率，下列说法中正确的是 A.n1n2，a红光，b蓝光 D.n1>n2，a蓝光，b红光 ‎ 解：由图可知，b光线经过三棱镜后的偏折角较小，因此折射率较小，是红光。‎ ‎2．全反射棱镜 横截面是等腰直角三角形的棱镜叫全反射棱镜。选择适当的入射点，可以使入射光线经过全反射棱镜的作用在射出后偏转90o（右图1）或180o（右图2）。要特别注意两种用法中光线在哪个表面发生全反射。‎ ‎【例8】 如图所示，自行车的尾灯采用了全反射棱镜的原理。它虽然本身不发光，但在夜间骑行时，从后面开来的汽车发出的强光照到尾灯后，会有较强的光被反射回去，使汽车司机注意到前面有自行车。尾灯的原理如图所示，下面说法中正确的是 （ C ）‎ A.汽车灯光应从左面射过来在尾灯的左表面发生全反射 B.汽车灯光应从左面射过来在尾灯的右表面发生全反射 C.汽车灯光应从右面射过来在尾灯的左表面发生全反射 D.汽车灯光应从右面射过来在尾灯的右表面发生全反射 ‎ ‎3．光的折射和色散 ‎ 一束白光经过三棱镜折射后形式色散，构成红橙黄绿蓝靛紫的七条彩色光带，形成光谱。红 紫 光谱的产生表明白光是由各种单色光组成的复色光，各种单色光的偏转角度不同。‎ ‎ 红 紫 偏转角 小 大 折射率n 小 大 同介质速率v 大 小 频率γ 小 大 波长λ 大 小 ‎4．玻璃砖——所谓玻璃砖一般指横截面为矩形的棱柱。当光线从上表面入射，从下表面射出时，其特点是：⑴射出光线和入射光线平行；⑵各种色光在第一次入射后就发生色散；⑶射出光线的侧移和折射率、入射角、玻璃砖的厚度有关；⑷可利用玻璃砖测定玻璃的折射率。‎ θ1‎ θ2‎ ‎【例9】 透明材料做成一长方体形的光学器材，要求从上表面射入的光线可能从右侧面射出，那么所选的材料的折射率应满足B A.折射率必须大于 B.折射率必须小于 C.折射率可取大于1的任意值 D.无论折射率是多大都不可能 ‎ 解：从图中可以看出，为使上表面射入的光线经两次折射后从右侧面射出，θ1和θ2都必须小于临界角C，即θ145°，n=1/sinC<，选B答案。 ‎