【物理】2018届一轮复习人教版直线运动的图象教案 3页

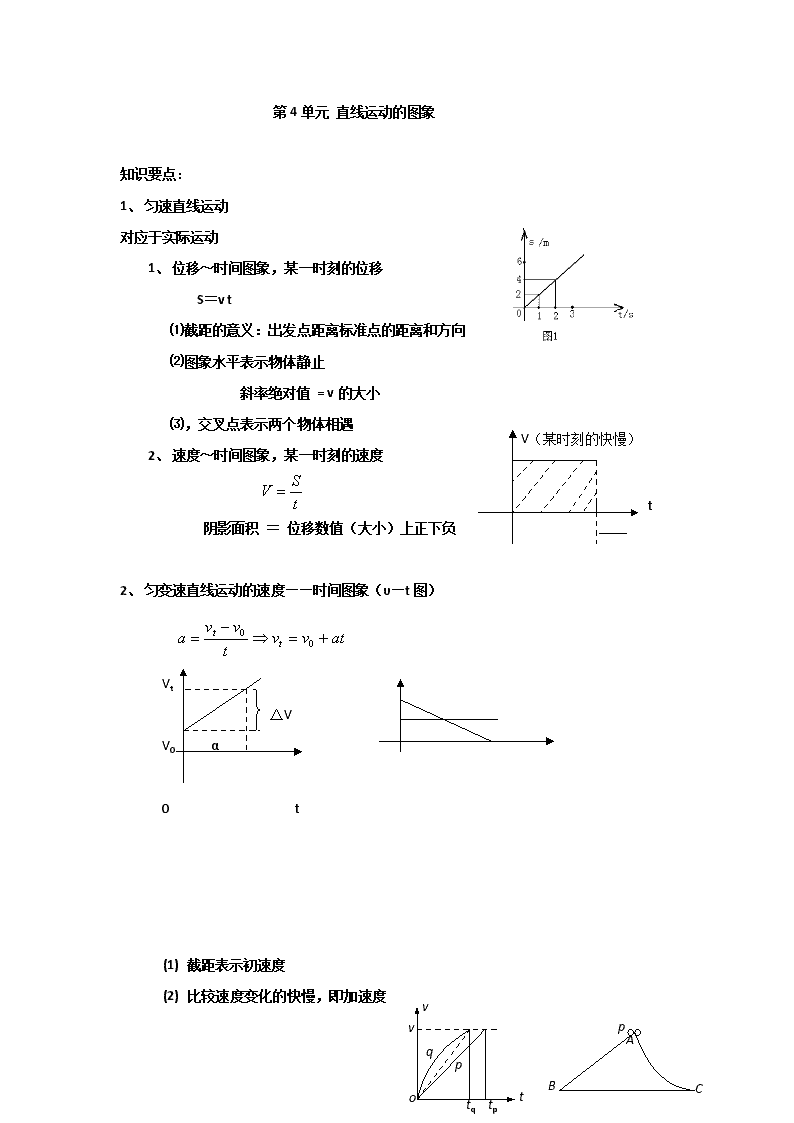
第4单元 直线运动的图象 知识要点：‎ 1、 匀速直线运动 对应于实际运动 ‎ 1、 位移～时间图象，某一时刻的位移 ‎ S＝v t ‎⑴截距的意义：出发点距离标准点的距离和方向 ‎⑵图象水平表示物体静止 ‎ 斜率绝对值 = v的大小 ‎⑶，交叉点表示两个物体相遇V（某时刻的快慢）‎ t 2、 速度～时间图象，某一时刻的速度 ‎ ‎ ‎ 阴影面积 ＝ 位移数值（大小）上正下负 2、 匀变速直线运动的速度——时间图象（υ—t图）‎ ‎ ‎ ‎△V ‎ Vt ‎ ‎ ‎ ‎ VO α ‎ ‎ ‎ ‎ 0 t ‎ ‎ (1) 截距表示初速度 ‎ p q A B C v t o ‎ p ‎ q v tq tp (2) 比较速度变化的快慢，即加速度 ‎ Z,xx,k.Com][ 学_科_网]‎ (1) 交叉点表示速度相等 (2) 面积 = 位移 上正下负 ‎【例1】 一个固定在水平面上的光滑物块，其左侧面是斜面AB，右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止 下滑，比较它们到达水平面所用的时间 A.p小球先到 B.q小球先到 C.两小球同时到 D.无法确定 v a a’‎ v1‎ v2‎ l1‎ l1‎ l2‎ l2‎ v t1‎ t2‎ t o vm 解：可以利用v-t图象(这里的v是速率，曲线下的面积表示路程s)定性地进行比较。在同一个v-t图象中做出p、q的速率图线，显然 时q的加速度较大，斜率较大；由于机械能守恒，末速率相同，即曲线末端在同一水平图线上。为使路程相同（曲线和横轴所围的面积相同），显然q用的时间较少。‎ ‎【例2】 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a/ 同时从管口由静止滑下，问谁先从下端的出口掉出？(假设通过拐角处时无机械能损失) ‎ 解析：首先由机械能守恒可以确定拐角处v1> v2，而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律，小球的加速度大小a=gsinα，小球a第一阶段的加速度跟小球a/第二阶段的加速度大小相同（设为a1）；小球a第二阶段的加速度跟小球a/第一阶段的加速度大小相同（设为a2），根据图中管的倾斜程度，显然有a1> a2。根据这些物理量大小的分析，在同一个v-t图象中两球速度曲线下所围的面积应该相同，且末状态速度大小也相同（纵坐标相同）。 时a球曲线的斜率大。由于两球两阶段加速度对应相等，如果同时到达（经历时间为t1）则必然有s1>s2，显然不合理。考虑到两球末速度大小相等（图中vm），球a/ 的速度图象只能如蓝线所示。因此有t1< t2，即a球先到。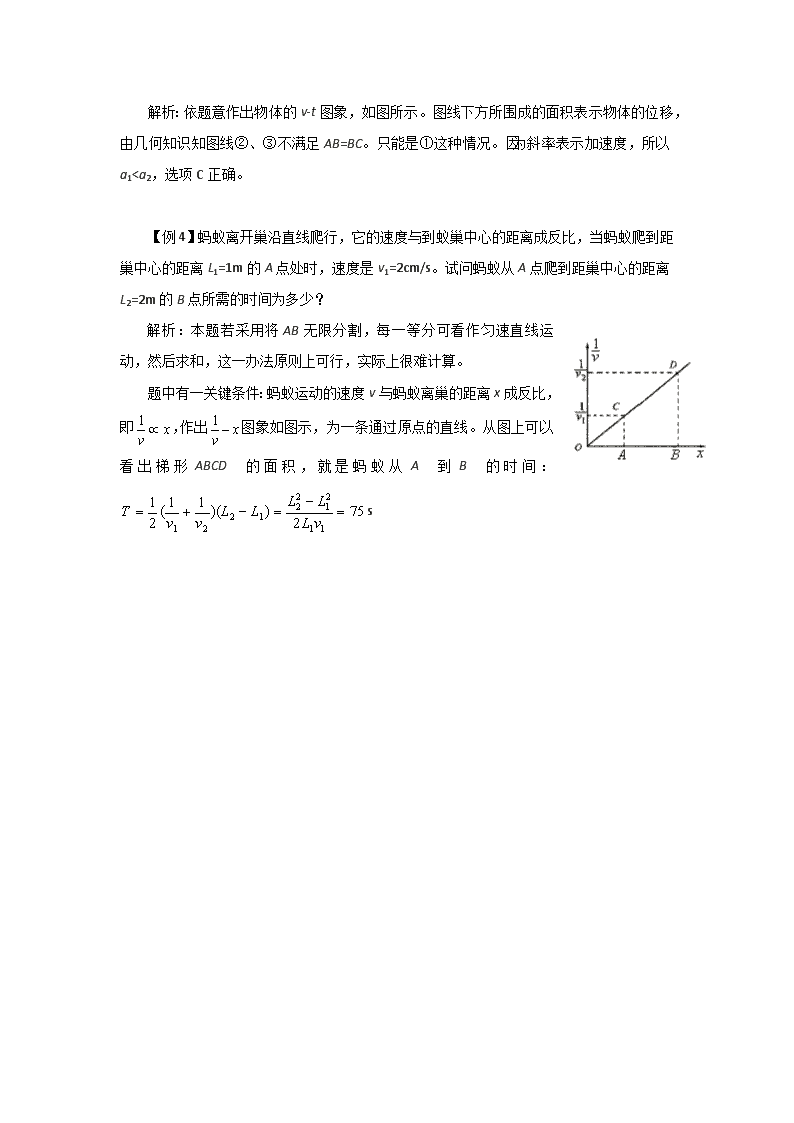‎ ‎【例3】一物体做加速直线运动，依次通过A、B、C三点，AB=BC。物体在AB段加速度为a1，在BC段加速度为a2，且物体在B点的速度为，则 A．a1> a2 B．a1= a2 ‎ C．a1< a2 D．不能确定 解析：依题意作出物体的v-t图象，如图所示。图线下方所围成的面积表示物体的位移，由几何知识知图线②、③不满足AB=BC。只能是①这种情况。因为斜率表示加速度，所以a1