【物理】2018届一轮复习人教版第14章机械振动机械波光电磁波与相对论学案 108页

第1节　机械振动 一、简谐运动 ‎1．概念：质点的位移与时间的关系遵从正弦函数的规律，即它的振动图象(x－t图象)是一条正弦曲线．‎ ‎2．简谐运动的表达式 ‎(1)动力学表达式：F＝－kx，其中“－”表示回复力与位移的方向相反．‎ ‎(2)运动学表达式：x＝Asin(ωt＋φ)，其中A代表振幅，ω＝2πf表示简谐运动的快慢，(ωt＋φ)代表简谐运动的相位，φ叫做初相．‎ ‎3．回复力 ‎(1)定义：使物体返回到平衡位置的力．‎ ‎(2)方向：时刻指向平衡位置．‎ ‎(3) 振动物体所受的沿振动方向的合力．‎ ‎4．描述简谐运动的物理量 物理量 定义 意义 振幅 振动质点离开平衡位置的最大距离 描述振动的强弱 周期 振动物体完成一次全振动所需时间 描述振动的快慢，两者互为倒数：T＝ 频率 振动物体单位时间内完成全振动的次数 相位 ωt＋φ 描述周期性运动在各个时刻所处的不同状态 二、简谐运动的图象 ‎1．物理意义：表示振子的位移随时间变化的规律，为正弦(或余弦)曲线．‎ ‎2．简谐运动的图象 ‎(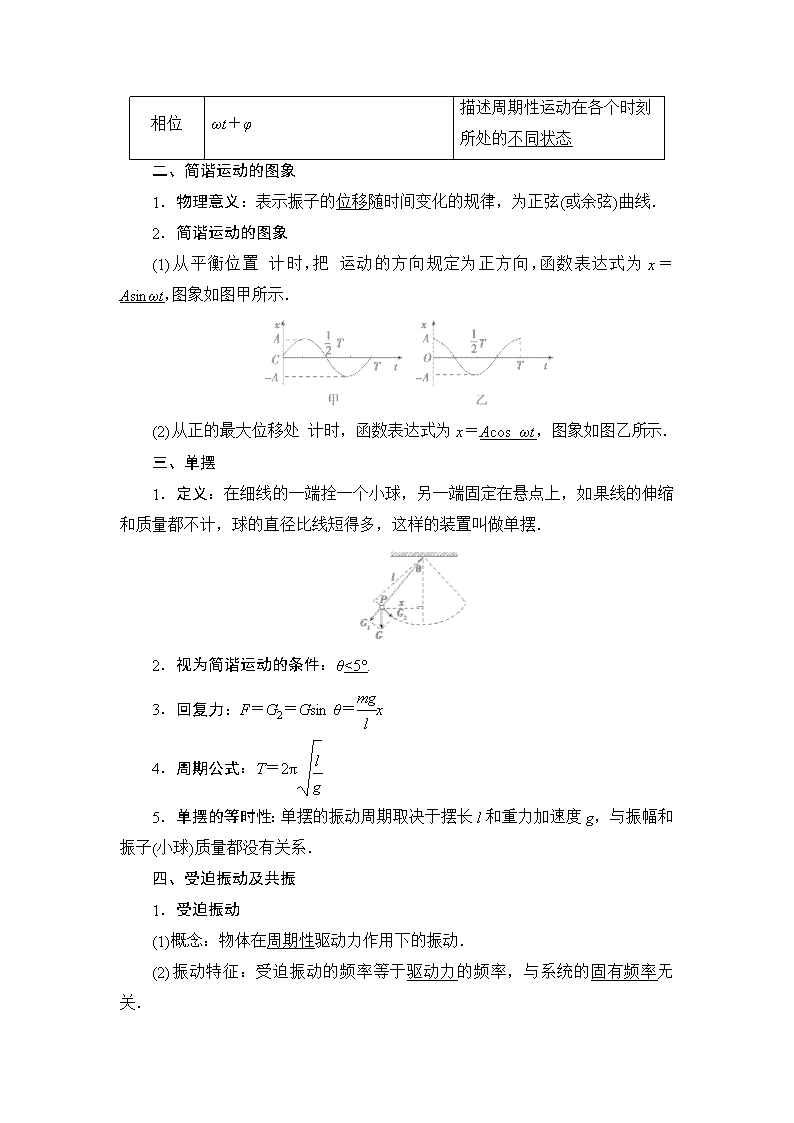1)从平衡位置 计时，把 运动的方向规定为正方向，函数表达式为x＝Asinωt，图象如图甲所示．‎ ‎(2)从正的最大位移处 计时，函数表达式为x＝Acos_ωt，图象如图乙所示．‎ 三、单摆 ‎1．定义：在细线的一端拴一个小球，另一端固定在悬点上，如果线的伸缩和质量都不计，球的直径比线短得多，这样的装置叫做单摆．‎ ‎2．视为简谐运动的条件：θ<5°.‎ ‎3．回复力：F＝G2＝Gsin θ＝x ‎4．周期公式：T＝2π.‎ ‎5．单摆的等时性：单摆的振动周期取决于摆长l和重力加速度g，与振幅和振子(小球)质量都没有关系．‎ 四、受迫振动及共振 ‎1．受迫振动 ‎(1)概念：物体在周期性驱动力作用下的振动．‎ ‎(2)振动特征：受迫振动的频率等于驱动力的频率，与系统的固有频率 无关．‎ ‎2．共振 ‎(1)概念：当驱动力的频率等于固有频率时，受迫振动的振幅最大的现象．‎ ‎(2)共振的条件：驱动力的频率等于固有频率．‎ ‎(3)共振的特征：共振时振幅最大．‎ ‎(4)共振曲线(如图所示)．‎ f＝f0时，A＝Am.f与f0差别越大，物体做受迫振动的振幅越小．‎ ‎[自我诊断]‎ ‎1．判断正误 ‎(1)简谐运动是匀变速运动．(×)‎ ‎(2)周期、频率和振幅都是表征物体做简谐运动快慢程度的物理量．(×)‎ ‎(3)振幅就是简谐运动物体的位移．(×)‎ ‎(4)简谐运动的回复力可以是恒力．(×)‎ ‎(5)物体做受迫振动时，其振动频率与固有频率无关．(√)‎ ‎(6)简谐运动的图象描述的是振动质点的轨迹．(×)‎ ‎2．做简谐运动的物体，当它每次经过同一位置时，可能不同的物理量是(　　)‎ A．位移　 B．速度 C．加速度 D．回复力 解析：选B.做简谐运动的物体，当它每次经过同一位置时，位移相同，加速度相同，速度的大小相等，但方向不一定相同，所以可能不同的物理量是速度，选项B正确．‎ ‎3．如图所示，弹簧振子在M、N之间做简谐运动．以平衡位置O为原点，建立Ox轴，向右为x轴正方向．若振子位于N点时 计时，则其振动图象为(　　)‎ 解析：选A.当弹簧振子在MN之间运动时，M、N为振动的最远点，OM、ON的距离为振幅，从N点计时粒子距O点最远，ON为正方向，A正确，B、C、D错误．‎ ‎4．(多选)如右图所示，A球振动后，通过水平细绳迫使B、C振动，振动达到稳定时，下列说法中正确的是(　　)‎ A．A、C振动周期相等 B．C的振幅比B的振幅小 C．C的振幅比B的振幅大 D．A、B、C的振动周期相等 解析：选ACD.A振动后，水平细绳上驱动力的周期TA＝2π，迫使B、C做受迫振动，受迫振动的频率等于施加的驱动力的频率，所以TA＝TB＝TC，A、D正确；而TC固＝2π＝TA，TB固＝2π＞TA，故C共振，B不共振，C的振幅比B的振幅大，B错误、C正确．‎ ‎5．一个质点在平衡位置O点附近做机械振动．若从O点 计时，经过3 s质点第一次经过M点(如图所示)；再继续运动，又经过2 s它第二次经过M点；则该质点第三次经过M点还需要的时间是________或________．‎ 解析：若质点从O点 向右运动，则tOM＝3 s，tMb＝2× s＝1 s，则有T＝16 s，解得第三次回到M还需要14 s.‎ 若质点从O点 向左运动，tMb＝1 s，tOaM＝3 s，又由tOaM＝T－tMb，得T＝ s，tOM＝ s，解得第三次回到M点还需要 s.‎ 答案：14 s　 s 考点一　简谐运动的特征 ‎1．动力学特征：F＝－kx，“－”表示回复力的方向与位移方向相反，k是比例系数，不一定是弹簧的劲度系数．‎ ‎2．运动学特征：简谐运动的加速度与物体偏离平衡位置的位移成正比，而方向相反，为变加速运动，远离平衡位置时，x、F、a、Ep均增大，v、Ek均减小，靠近平衡位置时则相反．‎ ‎3．运动的周期性特征：相隔T或nT的两个时刻振子处于同一位置且振动状态相同．‎ ‎4．对称性特征：‎ ‎(1)相隔或(n为正整数)的两个时刻，振子位置关于平衡位置对称，位移、速度、加速度大小相等，方向相反．‎ ‎(2)如图所示，振子经过关于平衡位置O对称的两点P、P′(OP＝OP′)时，速度的大小、动能、势能相等，相对于平衡位置的位移大小相等．‎ ‎(3)振子由P到O所用时间等于由O到P′所用时间，即tPO＝tOP′.‎ ‎(4)振子往复过程中通过同一段路程(如OP段)所用时间相等，即tOP＝tPO.‎ ‎5．能量特征：振动的能量包括动能Ek和势能Ep，简谐运动过程中，系统动能与势能相互转化，系统的机械能守恒．‎ ‎1．(多选)关于简谐运动的下列说法中，正确的是(　　)‎ A．位移减小时，加速度减小，速度增大 B．位移方向总跟加速度方向相反，跟速度方向相同 C．物体的运动方向指向平衡位置时，速度方向跟位移方向相反；背向平衡位置时，速度方向跟位移方向相同 D．水平弹簧振子朝左运动时，加速度方向跟速度方向相同，朝右运动时，加速度方向跟速度方向相反 解析：选AC.物体做简谐运动的加速度a＝－，可得位移减小时，加速度减小，速度增大，A正确．位移方向总跟加速度方向相反，但位移方向跟速度方向可能相同，也可能相反，B错误，C正确．水平弹簧振子朝左运动时，若振子在平衡位置右侧，加速度方向与速度方向相同，若振子在平衡位置左侧，加速度方向与速度方向相反，D错误．‎ ‎2．如图所示，弹簧振子在振动过程中，振子从a到b历时0.2 s，振子经a、b两点时速度相同，若它从b再回到a的最短时间为0.4 s，则该振子的振动频率为(　　)‎ A．1 Hz　 B．1.25 Hz C．2 Hz D．2.5 Hz 解析：选B.由简谐运动的对称性可知，tO b＝0.1 s，从b向右运动到最大位移的时间也为0.1 s，故＝0.2 s，解得T＝0.8 s，频率f＝＝1.25 Hz，选项B正确．‎ ‎3．(2017·山东济宁模拟)(多选)一简谐振子沿x轴振动，平衡位置在坐标原点．t＝0时刻振子的位移x＝－‎0.1 m；t＝ s时刻x＝‎0.1 m；t＝4 s时刻x＝‎0.1 m．该振子的振幅和周期可能为(　　)‎ A．‎0.1 m， s B．‎0.1 m,8 s C．‎0.2 m， s D．‎0.2 m,8 s 解析：选ACD.若振子的振幅为0.1 m， s＝T，s＝n1T，则周期最大值为 s，A正确，B错误；若振子的振幅为0.2 m，由简谐运动的对称性可知，当振子由x＝－0.1 m处运动到负向最大位移处再反向运动到x＝0.1 m处，再经n个周期时所用时间为 s，则T＝ s，所以周期的最大值为 s，且t＝4 s时刻x＝0.1 m，C正确；当振子由x＝－0.1 m经平衡位置运动到x＝0.1 m处，再经n个周期时所用时间为 s，则T＝s，所以此时周期的最大值为8 s，且t＝4 s时，x＝0.1 m，D正确．‎ 分析简谐运动的技巧 ‎(1)分析简谐运动中各物理量的变化情况时，一定要以位移为桥梁，位移增大时，振动质点的回复力、加速度、势能均增大，速度、动能均减小；反之，则产生相反的变化．另外，各矢量均在其值为零时改变方向．‎ ‎(2)分析过程中要特别注意简谐运动的周期性和对称性．‎ 考点二　简谐运动的公式和图象 ‎1．简谐运动的公式：‎ ‎(1)简谐运动中位移随时间变化的表达式叫振动方程，一般表示为x＝Asin(ωt＋φ)．‎ ‎(2)从平衡位置 计时，函数表达式为x＝Asin ωt，从最大位移处 计时，函数表达式为x＝Acos ωt.‎ ‎2．对简谐运动图象的认识：‎ ‎(1)简谐运动的图象是一条正弦或余弦曲线，如图所示．‎ ‎(2)图象反映的是位移随时间的变化规律，随时间的增加而延伸，图象不代表质点运动的轨迹．‎ ‎3．图象信息：‎ ‎(1)由图象可以得出质点做简谐运动的振幅、周期和频率．‎ ‎(2)可以确定某时刻质点离开平衡位置的位移．‎ ‎(3)可以确定某时刻质点回复力、加速度的方向：因回复力总是指向平衡位置，故回复力和加速度在图象上总是指向t轴．‎ ‎(4)确定某时刻质点速度的方向：速度的方向可以通过下一时刻位移的变化来判定，下一时刻位移如增加，振动质点的速度方向就是远离t轴，下一时刻位移如减小，振动质点的速度方向就是指向t轴．‎ ‎(5)比较不同时刻回复力、加速度的大小．‎ ‎(6)比较不同时刻质点的动能、势能的大小．‎ ‎[典例]　(2017·浙江台州检测)如图甲所示，弹簧振子以点O为平衡位置，在A、B两点之间做简谐运动．取向右为正方向，振子的位移x随时间t的变化如图乙所示，下列说法正确的是(　　)‎ A．t＝0.8 s时，振子的速度方向向左 B．t＝0.2 s时，振子在O点右侧‎6 cm处 C．t＝0.4 s和t＝1.2 s时，振子的加速度完全相同 D．t＝0.4 s到t＝0.8 s的时间内，振子的速度逐渐减小 解析　由图象乙可知t＝0.8 s时，振子在平衡位置向负方向运动，所以速度方向向左，选项A正确；t＝0.2 s时，振子远离平衡位置运动，速度逐渐减小，应在O点右侧大于6 cm处，选项B错误；t＝0.4 s和t＝1.2 s时，振子的加速度大小相同，方向相反，选项C错误；t＝0.4 s到t＝0.8 s的时间内，振子向平衡位置运动，速度逐渐增大，选项D错误．‎ 答案　A ‎“图象—运动结合法”分析图象问题 ‎(1)解此类题时，首先要理解x－t图象的意义，其次要把x－t图象与质点的实际振动过程联系起来．‎ ‎(2)图象上的一个点表示振动中的一个状态(位置、振动方向等)，图象上的一段曲线对应振动的一个过程，关键是判断好平衡位置、最大位移及振动方向．‎ ‎1．(2016·湖北武汉部分重点中学联考)一质点沿x轴做简谐运动，其振动图象如图所示．在1.5～2 s的时间内，质点的速度v、加速度a的大小的变化情况是(　　)‎ A．v变小，a变大　　　 B．v变小，a变小 C．v变大，a变小 D．v变大，a变大 解析：选A.由振动图象可知，质点在1.5～2 s的时间内向下振动，故质点的速度越来越小，位移逐渐增大，回复力逐渐变大，加速度逐渐变大，选项A正确．‎ ‎2．(2017·北京昌平三中检测)如图为弹簧振子的振动图象，由此可知(　　)‎ A．在t1时刻，振子的动能最大，所受的弹力最大 B．在t2时刻，振子的动能最大，所受的弹力最小 C．在t3时刻，振子的动能最大，所受的弹力最大 D．在t4时刻，振子的动能最大，所受的弹力最大 解析：选B.x－t图象的斜率表示速度，故在t1时刻，速度为零，动能为零，选项A错误；在t2时刻，速度最大，动能最大，位移为零，故回复力为零，弹力为零，选项B正确；在t3时刻，振子的速度为零，故动能为零，选项C错误；在t4时刻，速度最大，动能最大，位移为零，故回复力为零，弹力为零，选项D错误．‎ ‎3．(2016·湖北荆州江陵中学期中)如图所示为某弹簧振子在0～5 s内的振动图象，由图可知，下列说法中正确的是(　　)‎ A．振动周期为5 s，振幅为‎8 cm B．第2 s末振子的速度为零，加速度为负向的最大值 C．第3 s末振子的速度为正向的最大值 D．从第1 s末到第2 s末振子在做加速运动 解析：选C.根据图象，周期T＝4 s，振幅A＝8 cm，A错误．第2 s末振子到达波谷位置，速度为零，加速度为正向的最大值，B错误．第3 s末振子经过平衡位置，速度达到最大值，且向正方向运动，C正确．从第1 s末到第2 s末振子经过平衡位置向下运动到达波谷位置，速度逐渐减小，做减速运动，D错误．‎ ‎4．(多选)如图，轻弹簧上端固定，下端连接一小物块，物块沿竖直方向做简谐运动．以竖直向上为正方向，物块简谐运动的表达式为y＝0.1sin(2.5πt)m.t＝0时刻，一小球从距物块h高处自由落下；t＝0.6 s时，小球恰好与物块处于同一高度．取重力加速度的大小g＝‎10 m/s2.以下判断正确的是(　　)‎ A．h＝‎‎1.7 m B．简谐运动的周期是0.8 s C．0.6 s内物块运动的路程为‎0.2 m D．t＝0.4 s时，物块与小球运动方向相反 解析：选AB.由物块简谐运动的表达式y＝0.1 sin(2.5πt) m知，ω＝2.5π rad/s，T＝＝ s＝0.8 s，选项B正确；t＝0.6 s时，y＝－0.1 m，对小球：h＋|y|＝gt2，解得h＝1.7 m，选项A正确；物块0.6 s内路程为0.3 m，t＝0.4 s时，物块经过平衡位置向下运动，与小球运动方向相同．故选项C、D错误．‎ 考点三　受迫振动和共振 1． 自由振动、受迫振动和共振的关系比较 振动 项目　　‎ 自由振动 受迫振动 共振 受力情况 仅受回复力 受驱动力作用 受驱动力作用 振动周期或频率 由系统本身性质决定，即固有周期T0或固有频率f0‎ 由驱动力的周期或频率决定，即T＝T驱或f＝f驱 T驱＝T0或f驱＝f0‎ 振动能量 振动物体的机械能不变 由产生驱动力的物体提供 振动物体获得的能量最大 常见例子 弹簧振子或单摆(θ≤5°)‎ 机械工作时底座发生的振动 共振筛、声音的共鸣等 ‎2.对共振的理解 ‎(1)共振曲线：如图所示，横坐标为驱动力频率f，纵坐标为振幅A.它直观地反映了驱动力频率对某固有频率为f0的振动系统受迫振动振幅的影响，由图可知，f与f0越接近，振幅A越大；当f＝f0时，振幅A最大．‎ ‎(2)受迫振动中系统能量的转化：做受迫振动的系统的机械能不守恒，系统与外界时刻进行能量交换．‎ ‎1．(2016·陕西三模)在实验室可以做“声波碎杯”的实验，用手指轻弹一只玻璃酒杯，可以听到清脆的声音，测得这声音的频率为500 Hz.将这只酒杯放在一个大功率的声波发生器前，操作人员通过调整其发出的声波，就能使酒杯碎掉．下列说法中正确的是(　　)‎ A．操作人员必须把声波发生器输出的功率调到很大 B．操作人员必须使声波发生器发出频率很高的超声波 C．操作人员必须同时增大声波发生器发出声波的频率和功率 D．操作人员必须将声波发生器发出的声波频率调到500 Hz，且适当增大其输出功率 解析：选D.由题可知用手指轻弹一只酒杯，测得这声音的频率为500 Hz，就是酒杯的固有频率．当物体发生共振时，物体振动的振幅最大，甚至可能造成物体解体．将这只酒杯放在两只大功率的声波发生器之间，操作人员通过调整其发出的声波，将酒杯碎掉是利用的共振现象，而发生共振的条件是驱动力的频率等于物体的固有频率，而酒杯的固有频率为500 Hz，故操作人员要将声波发生器发出的声波频率调到500 Hz，使酒杯产生共振，从而能将酒杯碎掉，故D正确．‎ ‎2．如图所示，两个弹簧振子悬挂在同一支架上，已知甲弹簧振子的固有频率为8 Hz，乙弹簧振子的固有频率为72 Hz，当支架受到竖直方向且频率为9 Hz的驱动力作用做受迫振动时，两个弹簧振子的振动情况是(　　) ‎ A．甲的振幅较大，且振动频率为8 Hz B．甲的振幅较大，且振动频率为9 Hz C．乙的振幅较大，且振动频率为9 Hz D．乙的振幅较大，且振动频率为72 Hz 解析：选B.物体做受迫振动时，振动频率一定等于驱动力的频率，故甲和乙的振动频率都是9 Hz.再根据受迫振动的“振幅特征”可知，甲弹簧振子的固有频率更接近驱动力的频率，所以甲的振幅较大．综上知，B正确．‎ ‎3．(多选)如图所示为两单摆分别在受迫振动中的共振曲线，则下列说法正确的是(　　)‎ A．若两摆的受迫振动分别在月球上和地球上进行，且摆长相同，则图线Ⅰ 表示月球上单摆的共振曲线 B．若两摆的受迫振动是在地球上同一地点进行，则两摆摆长之比LⅠ∶LⅡ＝25∶4‎ C．图线Ⅱ若表示在地面上完成的，则该单摆摆长约为‎1 m D．若摆长均为‎1 m，则图线Ⅰ表示在地面上完成的 解析：选ABC.图线中振幅最大处对应的频率应与做受迫振动的单摆的固有频率相等，从图线上可以看出，两摆的固有频率fⅠ＝0.2 Hz，fⅡ＝0.5 Hz.当两摆在月球和地球上分别做受迫振动且摆长相等时，根据公式f＝可知，g越大，f越大，所以gⅡ＞gⅠ，因为g地＞g月，因此可推知图线Ⅰ表示月球上单摆的共振曲线，A正确；若在地球上同一地点进行两次受迫振动，g相同，摆长长的f小，且有＝，所以＝，B正确；fⅡ＝0.5 Hz，若图线Ⅱ表示在地面上完成的，根据g＝9.8 m/s2，可计算出LⅡ约为1 m，C正确，D错误．‎ 考点四　实验：探究单摆运动　用单摆测定重力加速度 ‎1．实验原理：由单摆的周期公式T＝2π，可得出g＝l，测出单摆的摆长l和振动周期T，就可求出当地的重力加速度g.‎ ‎2．实验器材：单摆、游标卡尺、毫米刻度尺、停表．‎ ‎3．实验步骤 ‎(1)做单摆：取约‎1 m长的细丝线穿过带中心孔的小钢球，并打一个比小孔大一些的结，然后把线的另一端用铁夹固定在铁架台上，让摆球自然下垂，如图所示．‎ ‎(2)测摆长：用毫米刻度尺量出摆线长L(精确到毫米)，用游标卡尺测出小球直径D，则单摆的摆长l＝L＋.‎ ‎(3)测周期：将单摆从平衡位置拉开一个角度(小于10°)，然后释放小球，记下单摆摆动30～50次的总时间，算出平均每摆动一次的时间，即为单摆的振动周期．‎ ‎(4)改变摆长，重做几次实验．‎ ‎(5)数据处理的两种方法：‎ 方法一：计算法．‎ 根据公式T＝2π，g＝.将测得的几次周期T和摆长l代入公式g＝中算出重力加速度g的值，再算出g的平均值，即为当地的重力加速度的值．‎ 方法二：图象法．‎ 由单摆的周期公式T＝2π可得l＝T2，因此以摆长l为纵轴，以T2为横轴作出的l－T2图象是一条过原点的直线，如图所示，求出图线的斜率k，即可求出g值．g＝4π2k，k＝＝.‎ ‎4．注意事项 ‎(1)悬线顶端不能晃动，需用夹子夹住，保证悬点固定．‎ ‎(2)单摆必须在同一平面内振动，且摆角小于10°.‎ ‎(3)选择在摆球摆到平衡位置处时 计时，并数准全振动的次数．‎ ‎(4)小球自然下垂时，用毫米刻度尺量出悬线长L，用游标卡尺测量小球的直径，然后算出摆球的半径r，则摆长l＝L＋r.‎ ‎(5)选用一米左右的细线．‎ ‎1．在“用单摆测定重力加速度”的实验中：‎ ‎(1)图甲中秒表示数为一单摆振动50次所需时间，则单摆的振动周期为________．‎ ‎(2)用最小刻度为‎1 mm的刻度尺测摆长，测量情况如图乙所示．O为悬挂点，从图中可知单摆的摆长为________．‎ ‎(3)若用l表示摆长，T表示周期，那么重力加速度的表达式为g＝________.‎ ‎(4)考虑到单摆振动时空气浮力的影响后，学生甲说：“因为空气浮力与摆球重力方向相反，它对球的作用相当于重力加速度变小，因此振动周期变大．”学生乙说：“浮力对摆球的影响好像用一个轻一些的摆球做实验，因此振动周期不变．”这两个学生中________．‎ A．甲说得对　　 B．乙说得对　　　‎ C．都说得不对 解析：(1)t＝2 min＋12.5 s＝132.5 s，T＝＝2.65 s ‎(2)摆长是从悬挂点到球心的距离，读数为‎990.0 mm＋‎6.5 mm(估计读数)＝‎996.5 mm.‎ ‎(3)由T＝2π，得g＝.‎ ‎(4)球的质量大小并不影响重力加速度的大小，而空气的浮力的存在，能够造成“看上去”重力加速度减小，故甲的说法是正确的．‎ 答案：(1)2.65 s　(2)996.5 mm　(3)　(4)A ‎2．(2017·四川雅安中学模拟)用单摆测重力加速度时，‎ ‎(1)摆球应采用直径较小，密度尽可能________的小球，摆线长度要在‎1米左右，用细而不易断的尼龙线．‎ ‎(2)摆线偏离竖直方向的最大角度θ应________．‎ ‎(3)要在摆球通过________位置时 计时并计为零次，摆线每经过此位置两次才完成一次全振动，摆球应在________面内摆动，利用单摆测重力加速度的实验中，摆长的测量应在摆球自然下垂的状况下从悬点量至________．‎ ‎(4)某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为L＝‎97.50 cm；用50分度的游标卡尺(测量值可准确到‎0.02 mm)测得摆球直径为d＝‎2.100 cm；然后用停表记录了单摆振动n＝50次全振动所用的时间为t＝99.9 s．则该摆摆长为________ cm，周期为________ s，计算重力加速度的表达式为________．‎ 解析：(1)用单摆测重力加速度时，由于存在空气阻力对实验的影响，为了减小这种影响，所以采用体积小、密度大的摆球．‎ ‎(2)当角度很小时，单摆运动可以看成是简谐运动，所以最大角度θ应小于5°.‎ ‎(3)本实验偶然误差主要来自于时间(单摆周期)的测量上，因此，要注意测准时间，从摆球通过平衡位置 计时，为了防止振动是圆锥摆，要在竖直平面内摆动，摆长是悬线的长度和小球半径之和．‎ ‎(4)真正的摆长为l＝L＋＝‎97.50 cm＋ cm＝‎98.550 cm，周期T＝＝ s＝1.998 s．根据周期公式T＝2π得出g＝，代入摆长和周期计算可得g＝.‎ 答案：(1)大　(2)小于5°　(3)平衡　同一竖直　摆球球心　(4)98.550　1.998　g＝2π2n2(2L＋d)/t2‎ ‎3．用单摆测定重力加速度的实验装置如图1所示．‎ ‎(1)(多选)组装单摆时，应在下列器材中选用________(选填选项前的字母)．‎ A．长度为‎1 m左右的细线 B．长度为‎30 cm左右的细线 C．直径为‎1.8 cm的塑料球 D．直径为‎1.8 cm的铁球 ‎(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n 次全振动所用的时间t，则重力加速度g＝________(用L、n、t表示)．‎ ‎(3)下表是某同学记录的3组实验数据，并做了部分计算处理.‎ 组次 ‎1‎ ‎2‎ ‎3‎ 摆长L/cm ‎80.00‎ ‎90.00‎ ‎100.00‎ ‎50次全振动时间t/s ‎90.0‎ ‎95.5‎ ‎100.5‎ 振动周期T/s ‎1.80‎ ‎1.91‎ 重力加速度g/(m·s－2)‎ ‎9.74‎ ‎9.73‎ 请计算出第3组实验中的T＝______s，g＝______m/s2.‎ ‎(4)用多组实验数据做出T2L图象，也可以求出重力加速度g.已知三位同学做出的T2L图线的示意图如图2中的a、b、c所示，其中a和b平行，b和c都过原点，图线b对应的g值最接近当地重力加速度的值．则相对于图线b，下列分析正确的是________(选填选项前的字母)．‎ A．出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L B．出现图线c的原因可能是误将49次全振动记为50次 C．图线c对应的g值小于图线b对应的g值 ‎(5)某同学在家里测重力加速度．他找到细线和铁锁，制成一个单摆，如图3所示，由于家里只有一根量程为0～‎30 cm的刻度尺，于是他在细线上的A点做了一个标记，使得悬点O到A点间的细线长度小于刻度尺量程．保持该标记以下的细线长度不变，通过改变O、A间细线长度以改变摆长．实验中，当O、A间细线的长度分别为l1、l2时，测得相应单摆的周期为T1、T2，由此可得重力加速度g＝________(用l1，l2，T1，T2表示)．‎ 解析：(1)组装单摆时，应选用1 m左右的细线，摆球应选择体积小、密度大的球，选项A、D正确．‎ ‎(2)单摆的振动周期T＝.‎ 根据T＝2π，得g＝＝.‎ ‎(3)T3＝＝2.01 s.‎ 根据T＝2π，得g＝≈9.76 m/s2.‎ ‎(4)根据T＝2π，得T2＝L，即当L＝0时，T2＝0.出现图线a的原因是计算摆长时过短，误将悬点O到小球上端的距离记为摆长，选项A错误；对于图线c，其斜率k变小了，根据k＝，可能是T变小了或L变大了．选项B中误将49次全振动记为50次，则周期T变小，选项B正确；由＝k得g＝，则k变小，重力加速度g变大，选项C错误．‎ ‎(5)设A点到铁锁重心的距离为l0.根据单摆的周期公式T＝2π，得T1＝2π　，T2＝2π　.联立以上两式，解得重力加速度g＝.‎ 答案：(1)AD　(2)　(3)2.01　9.76　(4)B ‎(5) ‎　‎ 用单摆测重力加速度的几点注意 ‎(1)该实验为测量性实验，要从多方面减小误差：摆球要体积小且密度大；偏角小于5°；测量摆长时，要从悬点到球心；对秒表要正确读数等．‎ ‎(2)游标卡尺读数规律和读数公式．‎ ‎①读数公式：读数＝主尺上的整毫米数＋精确度×n(n为游标尺上与主尺某一刻度对齐的格数)‎ ‎②读数位数：各种游标卡尺的读数结果若以毫米为单位，小数点后保留的位数与其精确度相同．‎ ‎③游标卡尺是根据刻度线对齐来读数的，所以不再往下一位估读．‎ ‎ (3)减少各种失误：如游标尺上的精度分析错误；把边框线误认为零刻线；计算失误等．‎ 课时规范训练 ‎[基础巩固题组]‎ ‎1．摆长为L的单摆做简谐运动，若从某时刻 计时(取t＝0)，当振动至t＝时，摆球具有负向最大速度，则单摆的振动图象是图中的(　　)‎ 解析：选C.单摆周期为T＝2π，当t＝＝时摆球具有负向最大速度，知摆球经过平衡位置向负方向振动，选项C正确，A、B、D错误．‎ ‎2．在飞机的发展史中有一个阶段，飞机上天后不久，飞机的机翼很快就抖动起来，而且越抖越厉害，后来人们经过了艰苦的探索，利用在飞机机翼前缘处装置一个配重杆的方法，解决了这一问题．在飞机机翼前装置配重杆的主要目的是(　　)‎ A．加大飞机的惯性 B．使机体更加平衡 C．使机翼更加牢固 D．改变机翼的固有频率 解析：选D.当驱动力的频率与物体的固有频率相等时，振幅较大，因此要减弱机翼的振动，必须改变机翼的固有频率，选D.‎ ‎3．做简谐运动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的，则单摆振动的(　　)‎ A．频率、振幅都不变 B．频率、振幅都改变 C．频率不变、振幅改变 D．频率改变、振幅不变 解析：选C.由单摆周期公式T＝2π知周期只与l、g有关，与m和v无关，周期不变，其频率不变；在没改变质量前，设单摆最低点与最高点高度差为h，最低点速度为v，则mgh＝mv2，质量改变后有4mgh′＝×4m·2，可知h′≠h，振幅改变，C正确．‎ ‎4．一个单摆在地面上做受迫振动，其共振曲线(振幅A与驱动力频率f的关系)如图所示，则下列说法正确的是(　　)‎ A．此单摆的固有周期约为0.5 s B．此单摆的摆长约为‎1 m C．若摆长增大，单摆的固有频率增大 D．若摆长增大，共振曲线的峰将向右移动 解析：选B.由共振曲线知此单摆的固有频率为0.5 Hz，固有周期为2 s；再由T＝2π，得此单摆的摆长约为1 m；若摆长增大，则单摆的固有周期增大，固有频率减小，共振曲线的峰将向左移动，B正确，A、C、D错误．‎ ‎5．(多选)如图甲所示的弹簧振子(以O点为平衡位置在B、C间振动)，取水平向右的方向为振子离开平衡位置的位移的正方向，得到如图乙所示的振动曲线，由曲线所给的信息可知，下列说法正确的是(　　)‎ A．t＝0时，振子处在B位置 B．振子运动的周期为4 s C．t＝4 s时振子对平衡位置的位移为‎10 cm D．t＝2.5 s时振子对平衡位置的位移为‎5 cm E．如果振子的质量为‎0.5 kg，弹簧的劲度系数20‎ ‎ N/cm，则振子的最大加速度大小为‎400 m/s2‎ 解析：选ABE.由图乙可知，振子做简谐振动的振幅为10 cm，其周期T＝4 s，t＝0和t＝4 s时，振子在负的最大位置，即图甲中的B位置．由于振子做变速运动，故t＝2.5 s时，振子的位移应大于5 cm，故选项A、B正确，C、D错误，由a＝－可知，振子的最大加速度为400 m/s2，选项E正确．‎ ‎6．(多选)一个质点经过平衡位置O，在A、B间做简谐运动，如图(a)所示，它的振动图象如图(b)所示，设向右为正方向，下列说法正确的是(　　)‎ A．OB＝‎‎5 cm B．第0.2 s末质点的速度方向是A→O C．第0.4 s末质点的加速度方向是A→O D．第0.7 s末时质点位置在O点与A点之间 E．在4 s内完成5次全振动 解析：选ACE.由图(b)可知振幅为5 cm，则OB＝OA＝5 cm，A项正确；由图可知0～0.2 s内质点从B向O运动，第0.2 s末质点的速度方向是B→O，B项错误；由图可知第0.4 s末质点运动到A点处，则此时质点的加速度方向是A→O，C项正确；由图可知第0.7 s末时质点位置在O与B之间，D项错误；由图(b)可知周期T＝0.8 s，则在4 s内完成全振动的次数为＝5，E项正确．‎ ‎7．(1)在利用单摆测定重力加速度的实验中．若测得的g值偏大，可能的原因是(　　)‎ A．摆球质量过大 B．单摆振动时振幅较小 C．测量摆长时，只考虑了线长，忽略了小球的半径 D．测量周期时，把n个全振动误认为(n＋1)个全振动，使周期偏小 E．测量周期时，把n个全振动误认为(n－1)个全振动，使周期偏大 ‎(2)若单摆是一个秒摆，将此摆移到月球上，其周期是________．‎ ‎(3)实验中停表的读数如图，为________ s.‎ 解析：(1)由单摆周期公式T＝2π可知，重力加速度g＝，进而知重力加速度与摆球质量无关，故A错误；重力加速度与单摆振动的振幅无关，故B错误；测量摆长时，只考虑了线长，忽略了小球的半径，摆长l偏小，由g＝可知，所测重力加速度偏小，故C错误；测量周期时，把n个全振动误认为(n＋1)个全振动，使周期偏小，由g＝可知，所测重力加速度偏大，故D正确；测量周期时，把n个全振动误认为(n－1)个全振动，使周期偏大，由g＝可知，所测重力加速度偏小，故E错误．‎ ‎(2)在地球上秒摆的周期T＝2 s，将秒摆移到月球上，其周期T＝2π＝T＝2 s.‎ ‎(3)由图示停表可知，分针示数为1 min＝60 s，秒针示数为10.8 s，则停表示数为60 s＋10.8 s＝70.8 s.‎ 答案：(1)D　(2)2 s　(3)70.8‎ ‎[综合应用题组]‎ ‎8．(多选)如图所示为同一地点的两单摆甲、乙的振动图象，下列说法中正确的是(　　)‎ A．甲、乙两单摆的摆长相等 B．甲摆的振幅比乙摆大 C．甲摆的机械能比乙摆大 D．在t＝0.5 s时有正向最大加速度的是乙摆 E．由图象可以求出当地的重力加速度 解析：选ABD.由图看出，两单摆的周期相同，同一地点g相同，由单摆的周期公式T＝2π得知，甲、乙两单摆的摆长l相等，故A正确；甲摆的振幅为10 cm，乙摆的振幅为7 cm，则甲摆的振幅比乙摆大，故B正确；尽管甲摆的振幅比乙摆大，两摆的摆长也相等，但由于两摆的质量未知，无法比较机械能的大小，故C错误；在t＝0.5 s时，甲摆经过平衡位置，振动的加速度为零，而乙摆的位移为负向最大，则乙摆具有正向最大加速度，故D正确；由单摆的周期公式T＝2π得g＝，由于单摆的摆长未知，所以不能求得当地的重力加速度，故E错误．‎ ‎9．如图甲所示是一个摆线长度可调的单摆振动的情景图，O是它的平衡位置，P、Q是小球所能到达的最高位置．小球的质量m＝‎0.4 kg，图乙是摆线长为l时小球的振动图象，g取‎10 m/s2.‎ ‎(1)为测量单摆的摆动周期，测量时间应从摆球经过________(填“O”“P”或“Q”)时 计时；测出悬点到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t，则重力加速度g＝________(用L、n、t表示)．‎ ‎(2)由图乙写出单摆做简谐运动的表达式，并判断小球在什么位置时加速度最大？最大加速度为多少？‎ 解析：‎ ‎(1)因摆球经过最低点的速度大，容易观察和计时，所以测量时间应从摆球经过最低点O 计时．单摆周期T＝，再根据单摆周期公式T＝2π，可解得g＝.‎ ‎(2)由图乙可知单摆的振幅A＝‎5 cm，ω＝＝ rad/s＝π rad/s，所以单摆做简谐运动的表达式为x＝5sin πt(cm)．‎ 小球在最大位移处的加速度最大，由图乙可看出此摆的周期是2 s，根据T＝2π，可求得摆长为L＝1 m，加速度最大值am＝＝＝ m/s2＝0.5 m/s2.‎ 答案：(1)O　　(2)x＝5sin πt(cm)　小球在最大位移处的加速度最大　0.5 m/s2‎ ‎10．弹簧振子以O点为平衡位置，在B、C两点间做简谐运动，在t＝0时刻，振子从O、B间的P点以速度v向B点运动；在t＝0.20 s时刻，振子速度第一次变为－v；在t＝0.50 s时刻，振子速度第二次变为－v.‎ ‎(1)求弹簧振子的振动周期T；‎ ‎(2)若B、C之间的距离为‎25 cm，求振子在4.00 s内通过的路程；‎ ‎(3)若B、C之间的距离为‎25 cm，从平衡位置 计时，写出弹簧振子位移表达式，并画出弹簧振子的振动图象．‎ 解析：(1)画出弹簧振子简谐运动示意图如图所示．‎ 由对称性可得T＝×4 s＝1 s ‎(2)若B、C之间距离为‎25 cm，‎ 则振幅A＝×25 cm＝12.5 cm 振子4.00 s内通过的路程s＝4×4×12.5 cm＝200 cm ‎(3)根据x＝Asin ωt，A＝‎12.5 cm，ω＝＝2π rad/s 得x＝12.5sin 2πt(cm)‎ 振动图象如图所示．‎ 答案：(1)1 s　(2)200 cm　(3)x＝12.5sin 2πt(cm)‎ 图象见解析图 第2节　机械波 一、机械波 ‎1．机械波的形成条件 ‎(1)有发生机械振动的波源．‎ ‎(2)有传播介质，如空气、水等．‎ ‎2．传播特点 ‎(1)传播振动形式、传递能量、传递信息．‎ ‎(2)质点不随波迁移．‎ ‎3．机械波的分类 机械波 二、描述机械波的物理量 ‎1．波长λ：在波动中振动相位总是相同的两个相邻质点间的距离．用“λ”表示．‎ ‎2．频率f：在波动中，介质中各质点的振动频率都是相同的，都等于波源的振动频率．‎ ‎3．波速v、波长λ和频率f、周期T的关系 公式：v＝＝λf.‎ 机械波的速度大小由介质决定，与机械波的频率无关．‎ 三、机械波的图象 ‎1．图象：在平面直角坐标系中，用横坐标表示介质中各质点的平衡位置 ‎，用纵坐标表示某一时刻各质点偏离平衡位置的位移，连接各位移矢量的末端，得出的曲线即为波的图象，简谐波的图象是正弦(或余弦)曲线．‎ ‎2．物理意义：某一时刻介质中各质点相对平衡位置的位移．‎ 四、波的衍射 ‎1．定义：波可以绕过障碍物继续传播的现象．‎ ‎2．发生明显衍射的条件：只有缝、孔的宽度或障碍物的尺寸跟波长相差不多，或者小于波长时，才会发生明显的衍射现象．‎ 五、波的干涉 ‎1．波的叠加原理：几列波相遇时能保持各自的运动状态，继续传播，在它们重叠的区域里，介质的质点同时参与这几列波引起的振动，质点的位移等于这几列波单独传播时引起的位移的矢量和．‎ ‎2．波的干涉 ‎(1)定义：频率相同的两列波叠加时，某些区域的振动加强、某些区域的振动减弱，这种现象叫波的干涉．‎ ‎(2)条件：两列波的频率相同．‎ ‎3．干涉和衍射是波特有的现象，波同时还可以发生反射、折射．‎ 六、多普勒效应 由于波源与观察者互相靠近或者互相远离时，接收到的波的频率与波源频率不相等的现象．‎ ‎[自我诊断]‎ ‎1．判断正误 ‎(1)在机械波的传播过程中，各质点随波的传播而迁移．(×)‎ ‎(2)相距一个(或整数个)波长的两个质点的振动位移在任何时刻都相同，而且振动速度的大小和方向也相同．(√)‎ ‎(3)两列波在介质中叠加，一定产生干涉现象．(×)‎ ‎(4)波的传播在时间上有周期性，在空间上也有周期性．(√)‎ ‎(5)机械波传递的是振动形式和能量．(√)‎ ‎(6)波的图象描述的是一个质点的位移随时间变化的关系．(×)‎ ‎(7)发生多普勒效应的原因是波在传播过程中频率发生了变化．(×)‎ ‎2．(多选)关于波的干涉、衍射等现象，下列说法正确的是(　　)‎ A．有的波只能发生干涉现象，有的波只能发生衍射现象 B．产生干涉现象的必要条件之一，就是两列波的频率相等 C．能观察到明显的衍射现象的条件是障碍物的尺寸与波长比较相差不多或比波长更小 D．在干涉图样中，振动加强区域中的质点，其位移始终最大，振动减弱区域的质点，其位移始终保持最小 E．当观测者靠近波源时，接收到的波的频率会大于波源的振动频率 解析：选BCE.干涉、衍射是波共有的特性，所以A错误．干涉具备两波频率相同、相位差恒定的条件，B正确．当满足d≤λ时产生明显的衍射现象，C正确．在干涉图样中，质点的位移随时间时刻发生变化，D错误．在多普勒效应中，观测者与波源相对靠近时，接收到的波的频率大于波源的振动频率，E正确．‎ ‎3．(多选)如图所示，一列简谐横波沿x轴正方向传播，波传到x＝‎1 m的P点时，P点 向下振动，此时为计时起点，已知在t＝0.4 s时PM间第一次形成图示波形，此时x＝‎4 m的M点正好在波谷．下列说法中正确的是(　　)‎ A．P点的振动周期为0.4 s B．M点 振动的方向沿y轴正方向 C．当M点 振动时，P点正好在波峰 D．这列波的传播速度是‎10 m/s E．从计时 的0.4 s内，P质点通过的路程为‎30 cm 解析：选ACD.根据t＝0.4 s时的波形和传播方向可知，此时P点再次经过平衡位置且向下振动，所以周期T＝0.4 s，A正确．所有质点的起振方向都应与振源的起振方向相同，所以M点 振动时沿y轴负方向，B错误．PM间平衡位置的距离为λ，当M点 振动时，P点已经振动了T，所以P点正好在波峰，C正确．由波形知，该波的波长λ＝4 m，所以波速v＝＝10 m/s，D正确．一个周期(‎ T＝0.4 s)内，P质点通过的路程s＝4A＝40 cm，E错误．‎ ‎4．一列简谐横波沿x轴正方向传播，t＝0时刻的波形如图所示，介质中质点P、Q分别位于x＝‎2 m、x＝‎4 m处．从t＝0时刻 计时，当t＝15 s时质点Q刚好第4次到达波峰．‎ ‎(1)求波速；‎ ‎(2)写出质点P做简谐运动的表达式(不要求推导过程)．‎ 解析：(1)设简谐横波的波速为v，波长为λ，周期为T，由图象知λ＝4 m．由题意知t＝15 s＝3T＋T①‎ 又v＝②‎ 联立①②式，代入数据得v＝1 m/s ‎(2)质点P做简谐运动的表达式为y＝0.2sin(0.5πt)m 答案：(1)1 m/s　(2)y＝0.2sin(0.5πt)m 考点一　波的图象及波速公式的应用 ‎1．波动图象的特点 ‎(1)质点振动nT(波传播nλ)时，波形不变．‎ ‎(2)在波的传播方向上，当两质点平衡位置间的距离为nλ时(n＝1,2,3…)，它们的振动步调总相同；当两质点平衡位置间的距离为(2n＋1)(n＝0,1,2,3…)时，它们的振动步调总相反．‎ ‎(3)波源质点的起振方向决定了它后面的质点的起振方向，各质点的起振方向与波源的起振方向相同．‎ ‎2．波动图象的信息 ‎(1)直接读取振幅A和波长λ，以及该时刻各质点的位移．‎ ‎(2)确定某时刻各质点加速度的方向，并能比较其大小．‎ ‎(3)结合波的传播方向可确定各质点的振动方向或由各质点的振动方向确定波的传播方向．‎ ‎3．波速与波长、周期、频率的关系为：v＝＝λf.‎ ‎1．(多选)如图所示为从波源 振动到经过一个周期T时在介质中形成的波形图．则据此图可知下列说法中正确的是(　　)‎ A．若N点是波源，则该时刻P点的速度最大 B．若N点是波源，则P点已振动了 C．若M点是波源，则P点已振动了 D．若M点是波源，则M点 振动的方向向上 E．若波向右传播，则此时M点正在向下振动 解析：选BCE.若N是波源，则此波向左传播，P点已振动T，此时速度为零，A错误，B正确．若M是波源，由“上下坡法”可知M点 向下振动，P点已振动T，C、E正确，D错误．‎ ‎2．(多选)一列沿x轴正方向传播的简谐横波在t＝0时刻的波形如图所示，质点P的x坐标为‎3 m．已知任意振动质点连续2次经过平衡位置的时间间隔为0.4 s．下列说法正确的是(　　)‎ A．波速为‎4 m/s B．波的频率为1.25 Hz C．x坐标为‎15 m的质点在t＝0.6 s时恰好位于波谷 D．x坐标为‎22 m的质点在t＝0.2 s时恰好位于波峰 E．当质点P位于波峰时，x坐标为‎17 m的质点恰好位于波谷 解析：选BDE.任意振动质点连续2次经过平衡位置的时间间隔为0.4 s，可知振动周期T＝0.8 s，频率f＝＝1.25 Hz，B正确．从题图中可以看出波长λ＝4 m，根据v＝λf，得v＝5 m/s，A错误．由于波在传播过程中具有空间周期性，x坐标为15 m处的质点运动规律与x＝3 m处相同，从t＝0时刻经过0.6 s，即经历周期，质点应位于平衡位置，C错误．用同样的方法可判断出D、E正确．‎ ‎3．(2017·湖北孝感调研)(多选)一列简谐横波沿x轴正方向传播，周期为T.在t＝0时的波形如图所示，波上有P、Q两点，其纵坐标分别为yP＝‎2 cm，yQ＝－‎2 cm，下列说法中正确的是(　　)‎ A．P点的振动形式传到Q点需要 B．P、Q在振动过程中，位移的大小总相等 C．在内，P点通过的路程为‎20 cm D．经过，Q点回到平衡位置 E．在相等时间内，P、Q两质点通过的路程相等 解析：选ABE.由图看出，P、Q两点所对应的平衡位置间的距离等于半个波长，因简谐横波传播过程中，在一个周期内传播一个波长，则P点的振动形式传到Q点需要半个周期，P、Q两点的振动情况总是相反，所以在振动过程中，它们的位移大小总是相等，故A、B正确．若图示时刻P点在平衡位置或最大位移处，在T内，P点通过的路程为：s＝5A＝5×4 cm＝20 cm，而实际上图示时刻，P点不在平衡位置或最大位移处，所以在T内，P点通过的路程不是20 cm，故C错误．‎ 图示时刻，Q点向下运动，速度减小，所以从图示位置运动到波谷的时间大于，再从波谷运动到平衡位置的时间为，所以经过T，Q点没有回到平衡位置，故D错误．由于P、Q两点的振动步调总是相反，所以在相等时间内，P、Q两质点通过的路程相等，故E正确．‎ ‎4．(2017·宁夏银川一中模拟)(多选)一列简谐横波在某时刻的波形如图所示，此时刻质点P的速度为v，经过1.0 s它的速度大小、方向第一次与v相同，再经过0.2 s它的速度大小、方向第二次与v相同，则下列判断中正确的是(　　)‎ A．波沿x轴负方向传播，波速为‎5 m/s B．波沿x轴正方向传播，波速为‎5 m/s C．若某时刻质点M到达波谷处，则质点P一定到达波峰处 D．质点M与质点Q的位移大小总是相等、方向总是相反 E．从图示位置 计时，在2.0 s时刻，质点P的位移为‎20 cm 解析：选ACE.根据图可得λ＝6 m，根据经过1.0 s它的速度大小、方向第一次与v相同，再经过0.2 s它的速度大小、方向第二次与v相同可得周期T＝1.2 s，根据公式可得v＝＝5 m/s.根据“走坡法”可得波沿－x方向传播，选项A正确，B错误；因为此时质点M与质点P两点平衡位置之间的距离是半个波长，属于反相点，即振动情况总是相反，若质点M到达波谷处，则质点P一定到达波峰处，选项C正确；‎ 质点M与质点Q不属于反相点，所以位移不是总是大小相等、方向相反，选项D错误；根据题中信息可得P从图示位置运动到波谷需要0.2 s，从波谷运动到波峰需要0.6 s，所以在2.0 s时刻，质点P正好运动到了波峰，所以位移为20 cm，选项E正确．‎ 判断波的传播方向与质点的振动方向的三种常见方法 ‎(1)上下坡法：沿波的传播方向，上坡时质点向下振动，下坡时质点向上振动，如图甲所示．‎ ‎(2)同侧法：波形图上某点表示传播方向和振动方向的箭头在图线同侧，如图乙所示．‎ ‎(3) 微平移法：将波形图沿传播方向平移Δx(Δx≤)，再由x轴上某一位置的两波形曲线上的点来判定，如图丙所示．‎ 考点二　波动图象和振动图象的综合 振动图象与波动图象的比较：‎ 两种图象 比较内容　　‎ 振动图象 波动图象 研究对象 一振动质点 沿波传播方向上的所有质点 图象意义 一质点位移随时间变化的规律 某时刻所有质点相对平衡位置的位移 图象特点 图象信息 ‎①振动周期、振幅②各时刻质点的位移、速度、加速度(包括大小、方向)‎ ‎①波长、振幅②任意一质点此时刻的位移③任意一质点在此时刻加速度方向 图象变化 随时间推移图象延续，但原有形状不变 随时间推移，图象沿传播方向平移 一完整曲线 对应横坐标 一个周期 一个波长 ‎[典例1]　(多选)图甲为一列简谐横波在t＝0.10 s时刻的波形图，P是平衡位置在x＝‎1.0 m处的质点，Q是平衡位置在x＝‎4.0 m处的质点；图乙为质点Q的振动图象．下列说法正确的是(　　)‎ A．在t＝0.10 s时，质点Q向y轴正方向运动 B．在t＝0.25 s时，质点P的加速度方向与y轴正方向相同 C．从t＝0.10 s到t＝0.25 s，该波沿x轴负方向传播了‎6 m D．从t＝0.10 s到t＝0.25 s，质点P通过的路程为‎30 cm E．质点Q简谐运动的表达式为y＝0.10sin 10πt(国际单位制)‎ 解析　由题图乙可知，在t＝0.10 s时，质点Q向y轴负方向运动，A错误．结合题图甲、乙可知，波沿x轴负方向传播，t＝0.25 s时P处于y轴的负方向，则其加速度沿y轴的正方向，B正确．由图甲知波长λ＝8 m，由图乙知周期T＝0.2 s，则波传播的速度v＝＝40 m/s，所以在t＝0.10 s到t＝0.25 s时间内波向x轴负方向传播的距离x＝vt＝6 m，C正确．从t＝0.10 s到t＝0.25 s，经历的时间t＝T，只有计时 时，振动质点处于平衡位置或振幅点处，其经过的路程才是30 cm，D错误．由图乙可知E正确．‎ 答案　BCE ‎“一分、一看、二找”巧解波的图象与 振动图象综合类问题 ‎(1)分清振动图象与波的图象．只要看清横坐标即可，横坐标为x则为波的图象，横坐标为t则为振动图象．‎ ‎(2)看清横、纵坐标的单位．尤其要注意单位前的数量级．‎ ‎(3)找准波的图象对应的时刻．‎ ‎(4)找准振动图象对应的质点．‎ ‎1．(2016·贵州贵阳二模)(多选)如图所示，甲为一列沿x轴传播的简谐波在t＝0.1 s时刻的波形图象，乙表示该波在传播介质中x＝‎2 m处的质点a从t＝0时起的振动图象．则(　　)‎ A．该波的周期是0.10 s B．该波沿x轴负方向传播 C．t＝0.05 s时，质点a在负的最大位移处 D．从t＝0.10 s到t＝0.25 s，质点a通过的路程为‎40 cm E．t＝0.25 s，x＝‎4 m处的质点b的加速度沿y轴负方向 解析：选BCE.由质点a的振动图象知，波的周期T＝0.20 s，A错误．t＝0.10 s时，质点a沿y轴正方向运动，所以波沿x轴负方向传播，B正确．质点a在T时(即t＝0.05 s时)的位置应在负的最大位移处，C正确．从t＝0.10 s到t＝0.25 s，质点a又振动了T，所以通过的路程为60 cm，D错误．质点b在t＝0.10 s时向y轴负方向运动，t＝0.25 s时振动到正向最大位移处，所以加速度沿y轴负方向，E正确．‎ ‎2．(2017·四川资阳一诊)(多选)某横波在介质中沿x轴传播，图甲是t＝1 s时的波形图，图乙是介质中x＝‎2 m处质点的振动图象，则下列说法正确的是(　　)‎ A．波沿x轴正向传播，波速为‎1 m/s B．t＝2 s时，x＝‎2 m处质点的振动方向为y轴负向 C．x＝‎1 m处质点和x＝‎2 m处质点振动步调总相同 D．在1 s的时间内，波动图象上任意质点通过的路程都是‎10 cm E．在t＝1 s到t＝2 s的时间内，x＝‎0.5 m处的质点运动速度先增大后减小 解析：选BDE.由图乙可知，t＝1 s时，x＝2 m处的质点向上振动，故波沿x轴负向传播，波速为v＝＝ m/s＝1 m/s，选项A错误；由图乙可知，t＝2 s时，x＝2 m处质点的振动方向为y轴负向，选项B正确；x＝1 m处质点和x＝2 m处质点间的距离相差半个波长，故振动步调总相反，选项C错误；因为1 s＝T，故在1 s的时间内，波动图象上任意质点通过的路程都是2A＝5 cm×2＝10 cm，选项D正确；在t＝1 s到t＝2 s的时间内，x＝0.5 m处的质点从波峰到波谷位置，故运动速度先增大后减小，选项E正确．‎ ‎3．(2016·山西八校联考)(多选)如图甲所示为一简谐波在t＝0时刻的图象，图乙所示为x＝‎4 m处的质点P的振动图象，则下列判断正确的是(　　)‎ A．这列波的波速是‎2 m/s B．这列波的传播方向沿x轴正方向 C．t＝3.5 s时P点的位移为‎0.2 m D．从t＝0时刻 P点的振动方程为y＝0.2sin(πt＋π)m E．从t＝0时刻 P点的振动方程为y＝0.2sinm 解析：选ACD.由图象可知波长λ＝4 m，周期T＝2 s，波速v＝＝2 m/s，选项A正确；t＝0时刻P点向－y方向振动，由波动和振动的关系可判断波沿x轴负方向传播，选项B错误；由质点P的振动图象知，t＝3.5 s＝1T，此时P点位于波峰位置，位移为0.2 m，选项C正确；由图乙知ω＝＝π rad/s，初相位为π，振动方程为y＝0.2sin(πt＋π)m，选项D正确，E错误．‎ ‎4．(2016·广东联考)一列简谐横波沿x轴正方向传播，t＝0时刻的波形如图甲所示，A、B、P和Q是介质中的四个质点，t＝0时刻波刚好传播到B 点，质点A的振动图象如图乙所示，则：‎ ‎(1)该波的传播速度是多大？‎ ‎(2)从t＝0到t＝1.6 s，质点P通过的路程为多少？‎ ‎(3)经过多长时间质点Q第二次到达波谷？‎ 解析：(1)由图乙知，质点的振动周期为T＝0.8 s.‎ 由图甲知，波长λ＝20 m，则波速v＝＝ m/s＝25 m/s.‎ ‎(2)振幅为‎2 m，从t＝0到t＝1.6 s时，质点P通过的路程为：s＝2×‎4A＝‎16 m.‎ ‎(3)质点P、Q的平衡位置之间的距离为：L＝‎85 m－‎10 m＝‎75 m，由L＝vt，解得t＝3 s，即经过3 s时间质点Q第一次到达波谷，经过3.8 s时间质点Q第二次到达波谷．‎ 答案：(1)25 m/s　(2)16 m　(3)3.8 s 考点三　机械波的多解问题 ‎1．造成波动问题多解的主要因素有 ‎(1)周期性：‎ ‎①时间周期性：时间间隔Δt与周期T的关系不明确；‎ ‎②空间周期性：波传播距离Δx与波长λ的关系不明确．‎ ‎(2)双向性：‎ ‎①传播方向双向性：波的传播方向不确定；‎ ‎②振动方向双向性：质点振动方向不确定．‎ ‎2．解决波的多解问题的思路 一般采用从特殊到一般的思维方法，即找出一个周期内满足条件的关系Δt或Δx，若此关系为时间，则t＝nT＋Δt(n＝0,1,2…)；若此关系为距离，则x＝nλ＋Δx(n＝0,1,2…)．‎ ‎3．求解波的多解问题的一般步骤 ‎(1)根据初、末两时刻的波形图确定传播距离与波长的关系通式．‎ ‎(2)根据题设条件判断是唯一解还是多解．‎ ‎(3)根据波速公式v＝或v＝＝λf求波速．‎ ‎[典例2]　甲、乙两列简谐横波在同一介质中分别沿x轴正向和负向传播，波速均为v＝‎25 cm/s.两列波在t＝0时的波形曲线如图所示．求：‎ ‎(1)t＝0时，介质中偏离平衡位置位移为‎16 cm的所有质点的x坐标；‎ ‎(2)从t＝0 ，介质中最早出现偏离平衡位置位移为－‎16 cm的质点的时间．‎ 解析　(1)t＝0时，在x＝50 cm处两列波的波峰相遇，该处质点偏离平衡位置的位移为16 cm.两列波的波峰相遇处的质点偏离平衡位置的位移均为16 cm.‎ 从图线可以看出，甲、乙两列波的波长分别为 λ1＝‎50 cm，λ2＝‎60 cm①‎ 甲、乙两列波波峰的x坐标分别为 x1＝50＋k1λ1，k1＝0，±1，±2，…②‎ x2＝50＋k2λ2，k2＝0，±1，±2，…③‎ 由①②③式得，介质中偏离平衡位置位移为16 cm的所有质点的x坐标为 x＝(50＋300n) cm　(n＝0，±1，±2，…)④‎ ‎(2)只有两列波的波谷相遇处的质点的位移为－‎16 cm.‎ t＝0时，两列波波谷间的x坐标之差为 Δx′＝[50＋(‎2m2‎＋1)]－[50＋(‎2m1＋1)]⑤‎ 式中，m1和m2均为整数，将①式代入⑤式得 Δx′＝10×(‎6m2‎－‎5m1)＋5⑥‎ 由于m1、m2均为整数，相向传播的波谷间的距离最小为Δx0′＝5 cm⑦‎ 从t＝0 ，介质中最早出现偏离平衡位置位移为－16 cm的质点的时间为 t＝⑧‎ 代入数值得 t＝0.1 s⑨‎ 答案　(1)x＝(50＋300n) cm　(n＝0，±1，±2，…) (2)0.1 s 波的多解问题中几点注意 ‎(1)首先考虑双向性，若题目未告知波的传播方向或没有其他条件暗示，应首先按波传播的可能性进行讨论．‎ ‎(2)对设定的传播方向，确定Δt和T的关系，一般先确定最简单的情况，即一个周期内的情况，然后在此基础上加nT.‎ ‎(3)应注意题目是否有限制条件，如有的题目限制波的传播方向，或限制时间Δt大于或小于一个周期等，所以解题时应综合考虑，加强多解意识，认真分析题意．‎ ‎(4)空间的周期性与时间的周期性是一致的，实质上是波形平移规律的应用，所以应用时我们可以针对不同题目选择其中一种方法求解．‎ ‎1．(多选)一列简谐横波沿x轴正方向传播，t＝0时刻的波形如图中实线所示，t＝0.1 s时刻的波形如图中虚线所示．波源不在坐标原点O，P是传播介质中离坐标原点xP＝‎2.5 m处的一个质点．则以下说法正确的是(　　)‎ A．质点P的振幅为‎0.1 m B．波的频率可能为7.5 Hz C．波的传播速度可能为‎50 m/s D．在t＝0.1 s时刻与P相距‎5 m处的质点一定沿x轴正方向运动 E．在t＝0.1 s时刻与P相距‎5 m处的质点可能是向上振动，也可能是向下振动 解析：选ACE.质点P的振幅为0.1 m，选项A正确；波沿x轴正方向传播，t＝0.1 s内传播的距离至少为λ，即传播的距离Δx＝λ＝(4n＋1)m，t＝ T，故周期通式T＝ s(n＝0,1,2，…)，选项B错误；波速通式v＝Δx/t＝10(4n＋1)m/s(n＝0,1,2，…)，当n＝1时，v＝50 m/s，选项C正确；波的传播过程是振动形式的传播，质点不会沿波传播方向运动，选项D错误；在t＝0.1 s时刻与P相距5 m处的质点可能是向上振动，也可能是向下振动，选项E正确．‎ ‎2．(2017·吉林实验中学一模)(多选)一列简谐横波沿x轴正方向传播，t时刻波形图如图中的实线所示，此时波刚好传到P点，t＋0.6 s时刻，这列波刚好传到Q点，波形如图中的虚线所示，a、b、c、P、Q是介质中的质点，则以下说法正确的是(　　)‎ A．这列波的波速为‎16.7 m/s B．这列波的周期为0.8 s C．质点c在这段时间内通过的路程一定等于‎30 cm D．从t时刻 计时，质点a第一次到达平衡位置时，恰好是t＋ s这个时刻 E．当t＋0.5 s时刻，质点b、P的位移相同 解析：选BDE.由图可知，波的波长为40 m,0.6 s＝T，故周期为T＝(n＝0,1,2，…)，波速为v＝＝(4n＋3)m/s(n＝0,1,2，…)，把n＝0代入得T＝0.8 s，v＝50 m/s，选项A错误，B正确；因为c只振动了半个周期，故路程为2A＝20 cm，选项C错误；a点在实线位置时向上振动，第一次到达平衡位置时，根据对称性可得恰好是t＋ s这个时刻，D正确；‎ 在t时刻，因波沿x轴正方向传播，所以此时质点P是向上振动的，经0.5 s后，P正在向下振动(负位移)，是经过平衡位置后向下运动0.1 s；而质点b正在向上振动(负位移)，是到达最低点后向上运动0.1 s，因为0.2 s＝ ‎，可见此时两个质点的位移是相同的，选项E正确．‎ ‎3．(2016·陕西师大附中第二次模拟)一列简谐横波，沿波的传播方向依次有P、Q两点，平衡位置相距‎5.5 m，其振动图象如图所示，实线为P点的振动图象，虚线为Q点的振动图象，求：‎ ‎(1)该波的波长；‎ ‎(2)该波的最大传播速度．‎ 解析：(1)根据题意，画出如图所示的波动图象，‎ 其对应的方程y＝－10sin x，当y＝5时，sin x＝－ 解得x＝2nπ＋π(n＝0、1、2、3、…)‎ 根据数学关系类比可得 ＝(n＝0、1、2、3、…)‎ nλ＋λ＝5.5(n＝0、1、2、3、…)‎ 解得λ＝m(n＝0、1、2、3、…)‎ ‎(2)由图象可知：周期T＝1 s，由波速公式可得 v＝＝ m/s(n＝0、1、2、3、…)‎ 当n＝0时，vm＝6 m/s 答案：(1) m(n＝0、1、2、3、…)　(2)6 m/s 考点四　波的干涉、衍射、多普勒效应 ‎1．波的干涉中振动加强点和减弱点的判断 某质点的振动是加强还是减弱，取决于该点到两相干波源的距离之差Δr.‎ ‎(1)当两波源振动步调一致时 若Δr＝nλ(n＝0,1,2，…)，则振动加强；‎ 若Δr＝(2n＋1)(n＝0,1,2，…)，则振动减弱．‎ ‎(2)当两波源振动步调相反时 若Δr＝(2n＋1)(n＝0,1,2，…)，则振动加强；‎ 若Δr＝nλ(n＝0,1,2，…)，则振动减弱．‎ ‎2．波的衍射现象是指波能绕过障碍物继续传播的现象，产生明显衍射现象的条件是缝、孔的宽度或障碍物的尺寸跟波长相差不大或者小于波长．‎ ‎3．多普勒效应的成因分析 ‎(1)接收频率：观察者接收到的频率等于观察者在单位时间内接收到的完全波的个数．当波以速度v通过观察者时，时间t内通过的完全波的个数为N＝，因而单位时间内通过观察者的完全波的个数，即接收频率．‎ ‎(2)当波源与观察者相互靠近时，观察者接收到的频率变大，当波源与观察者相互远离时，观察者接收到的频率变小．‎ ‎1．(多选)如右图所示为观察水面波衍射的实验装置，AC和BD是两块挡板，AB是一个小孔，O是波源，图中已画出波源所在区域波的传播情况，每两条相邻波纹(图中曲线)之间的距离表示一个波长，则对波经过孔后的传播情况，下列描述正确的是(　　)‎ A．此时能明显观察到波的衍射现象 B．挡板前后波纹间距相等 C．如果将孔AB扩大，有可能观察不到明显的衍射现象 D．如果孔的大小不变，使波源频率增大，能更明显地观察到衍射现象 解析：选ABC.由题图可以看出，孔AB尺寸与波长相差不大，因只有缝、孔的宽度或障碍物的尺寸跟波长相差不多，或者比波长更小时，才能观察到明显的衍射现象，A、C正确；由λ＝知，v不变，f增大，λ减小，衍射现象不明显，D错误；既然衍射是指“波绕过障碍物而传播的现象”，那么经过孔后的波长自然不变，B正确．‎ ‎2．(2016·南昌二模)(多选)水面上两列频率相同的波在某时刻的叠加情况如图所示，以波源S1、S2为圆心的两组同心圆弧分别表示同一时刻两列波的波峰(实线)和波谷(虚线)．S1的振幅A1＝‎4 cm，S2的振幅A2＝‎3 cm，则下列说法正确的是(　　)‎ A．质点D是振动减弱点 B．质点A、D在该时刻的高度差为‎14 cm C．再过半个周期，质点B、C是振动加强点 D．质点C的振幅为‎1 cm E．质点C此刻以后将向下振动 解析：选BDE.由题图可知，D点为两波谷相遇，应该是加强点，选项A错误；此时A点在加强后的最高点，D点在加强后的最低点，由波的叠加可知AD的高度差为14 cm，选项B正确；由于两波的频率相等，叠加后会形成稳定的干涉图象，所以A、D点始终是加强点，B、C点始终是减弱点，选项C错误；质点C为减弱点，振幅为两振幅之差为1 cm，选项D正确；由题意可知此时质点C将向下振动，选项E正确．‎ ‎3．(1)(多选)一渔船向鱼群发出超声波，若鱼群正向渔船靠近，则被鱼群反射回来的超声波与发出的超声波相比(　　)‎ A．波速变大　 B．波速不变 C．频率变高 D．频率不变 ‎(2)用2×106 Hz的超声波检查胆结石，该超声波在结石和胆汁中的波速分别为2 ‎250 m/s和1 ‎‎500 m ‎/s，则该超声波在结石中的波长是胆汁中的______倍．用超声波检查胆结石是因为超声波的波长较短，遇到结石时_____(填“容易”或“不容易”)发生衍射．‎ 解析：(1)超声波的波速由介质决定，介质不变，则波速不变，B正确．当鱼群向渔船靠近时，由于多普勒效应，被鱼群反射回来的超声波频率高于波源发出的频率，C正确．‎ ‎(2)由于波长、波速、频率三者的关系为v＝λf，而同一超声波在不同介质中传播时频率不变(不发生多普勒效应)，则波长之比等于波速之比，所以该超声波在结石中的波长是胆汁的＝1.5倍；发生明显衍射现象的条件是缝、孔的宽度或障碍物的尺寸与波长相差不多，或小于波长．因为超声波的波长较短，所以遇到结石不容易发生衍射．‎ 答案：(1)BC　(2)1.5　不容易 ‎4．如图所示，在某一均匀介质中，A、B是振动情况完全相同的两个波源，其简谐运动表达式均为x＝0.1sin(20πt)m，介质中P点与A、B两波源间的距离分别为‎4 m和‎5 m，两波源形成的简谐横波分别沿AP、BP方向传播，波速都是‎10 m/s.‎ ‎(1)求简谐横波的波长；‎ ‎(2)P点的振动________(填“加强”或“减弱”)．‎ 解析：(1)设简谐波的速度为v，波长为λ，周期为T，由题意知T＝＝0.1 s 波速v＝ 代入数据得λ＝1 m ‎(2)因为xPB－xPA＝‎1 m＝λ，所以P点的振动加强．‎ 答案：(1)1 m　(2)加强 课时规范训练 ‎[基础巩固题组]‎ ‎1．(多选)某同学漂浮在海面上，虽然水面波正平稳地以‎1.8 m/s的速率向着海滩传播，但他并不向海滩靠近．该同学发现从第1个波峰到第10个波峰通过身下的时间间隔为15 s．下列说法正确的是(　　)‎ A．水面波是一种机械波 B．该水面波的频率为6 Hz C．该水面波的波长为‎3 m D．水面波没有将该同学推向岸边，是因为波传播时能量不会传递出去 E．水面波没有将该同学推向岸边，是因为波传播时振动的质点并不随波迁移 解析：选ACE.水面波是一种机械波，说法A正确．根据题意得周期T＝ s＝ s，频率f＝＝0.6 Hz，说法B错误．波长λ＝＝ m＝3 m，说法C正确．波传播过程中，传播的是振动形式，能量可以传递出去，但质点并不随波迁移，说法D错误，说法E正确．‎ ‎2．(多选)一振动周期为T、振幅为A、位于x＝0点的波源从平衡位置沿y轴正向 做简谐运动．该波源产生的一维简谐横波沿x轴正向传播，波速为v，传播过程中无能量损失．一段时间后，该振动传播至某质点P，关于质点P振动的说法正确的是(　　)‎ A．振幅一定为A B．周期一定为T C．速度的最大值一定为v D． 振动的方向沿y轴向上或向下取决于它离波源的距离 E．若P点与波源距离s＝vT，则质点P的位移与波源的相同 解析：选ABE.波传播过程中，各振动质点的振动周期、振幅、起振方向都和波源相同，A、B正确，D错误；质点的振动速度大小跟波速无关，C错误；s＝vT，则s等于一个波长，即P 点与波源相位相同，振动情况总相同，位移总相同，E正确．‎ ‎3．(多选)一列简谐横波从左向右以v＝‎2 m/s的速度传播，某时刻的波形图如图所示，下列说法正确的是(　　)‎ A．A质点再经过一个周期将传播到D点 B．B点正在向上运动 C．B点再经过T回到平衡位置 D．该波的周期T＝0.05 s E．C点再经过T将到达波峰的位置 解析：选BDE.质点不随波迁移，选项A错误；由波沿x轴向右传播可知B点正向上运动，选项B正确；B点向上运动靠近平衡位置过程中平均速度变大，所用时间小于八分之一周期，选项C错误；由T＝可知周期为0.05 s，选项D正确；C点向下运动，所以经过四分之三周期到达波峰，选项E正确．‎ ‎4．(多选)图甲为一列简谐横波在t＝2 s时的波形图，图乙为媒质中平衡位置在x＝‎1.5 m处的质点的振动图象，P是平衡位置为x＝‎2 m的质点，下列说法中正确的是(　　)‎ A．波速为‎0.5 m/s B．波的传播方向向右 C．0～2 s时间内，P运动的路程为‎8 cm D．0～2 s时间内，P向y轴正方向运动 E．当t＝7 s时，P恰好回到平衡位置 解析：选ACE.由振动图象知，周期T＝4 s，由波的图象知，波长λ＝2‎ ‎ m，波速v＝＝0.5 m/s，A正确；又由振动图象知，x＝1.5 m处的质点在t＝2 s时在平衡位置且向下振动，则波应该向左传播，B错误；则0～2 s内P运动的路程为8 cm，C正确；由于t＝2 s时的波形如题图甲，则0～2 s内P向y轴负方向运动，D错误；Δt＝7 s＝1T，P质点恰好回到平衡位置，E正确．‎ ‎5．(多选)一列简谐横波沿x轴正方向传播，在x＝‎12 m处的质点的振动图线如图甲所示，在x＝‎18 m处的质点的振动图线如图乙所示，下列说法正确的是(　　)‎ A．该波的周期为12 s B．x＝‎12 m处的质点在平衡位置向上振动时，x＝‎18 m处的质点在波峰 C．在0～4 s内x＝‎12 m处和x＝‎18 m处的质点通过的路程均为‎6 cm D．该波的波长可能为‎8 m E．该波的传播速度可能为‎2 m/s 解析：选ABD.根据题图甲可知，该波的周期为12 s，A正确．根据图甲和图乙，x＝12 m处的质点在平衡位置向上振动时，x＝18 m处的质点在波峰，B正确．x＝18 m处质点的振动方程为y＝4sin t，在0～4 s内质点通过的路程为(8－2)cm，C错误．两质点间的距离Δx可能满足Δx＝λ＝6 m，当n＝0时，λ＝8 m，D正确．这列波的波速v＝＝ m/s＝ m/s，无论n取何值，该波的传播速度都不可能为2 m/s，E错误．‎ ‎6．(多选)从O点发出的甲、乙两列简谐横波沿x轴正方向传播，某时刻两列波分别形成的波形如图所示，P点在甲波最大位移处，Q 点在乙波最大位移处，下列说法中正确的是(　　)‎ A．两列波具有相同的波速 B．两列波传播相同距离时，乙波所用的时间比甲波的短 C．P点比Q点先回到平衡位置 D．P质点完成20次全振动的时间内Q质点可完成30次全振动 E．若甲、乙两列波在空间相遇时不会发生干涉 解析：选ADE.两列简谐横波在同一介质中传播，波速相同，传播相同距离所用时间相同，故A正确，B错误．由图可知，两列波的波长之比λ甲∶λ乙＝3∶2，波速相同，由波速公式v＝得周期之比为T甲∶T乙＝3∶2，Q点与P点都要经过周期才回到平衡位置，所以Q点比P点先回到平衡位置，故C错误．两列波的频率之比为f甲∶f乙＝2∶3，则在P质点完成20次全振动的时间内Q质点完成30次全振动，故D正确．两列波的频率不同，不能产生稳定的干涉图样，故E正确．‎ ‎7．(多选)如图所示，同一均匀介质中的一条直线上有相距‎6 m的两个振幅相等的振源A、B.从t＝0时刻起，质点A、B同时 振动，且都只振动了一个周期．图甲为A的振动图象，图乙为B的振动图象．若A向右传播的波与B向左传播的波在0.3 s时相遇，则下列说法正确的是(　　)‎ A．两列波的波长都是‎2 m B．两列波在A、B间的传播速度均为‎10 m/s C．在两列波相遇过程中，A、B连线的中点C为振动加强点 D．在0.9 s时，质点B经过平衡位置且振动方向向上 E．两个波源振动的相位差为π 解析：选ABE.两列波在均匀介质中传播速度相同，设为v，则有2vt1＝xAB，代入解得v＝＝10 m/s，故B正确．由题图知周期T＝0.2 s，则波长λ＝vT＝2 m，故A正确．当A的波峰(或波谷)传到C时，恰好B的波谷(或波峰)传到C点，所以C点的振动始终减弱，故C错误．t2＝0.9 s＝4T时，质点B不振动，故D错误．振源A的简谐运动方程为y＝Asin ωt，振源B的简谐运动方程为y＝－Asin ωt＝Asin(ωt－π)，两个波源振动的相位差为π，故E正确．‎ ‎8．(多选)如图所示，图甲为一列简谐横波在t＝0.50 s时的波形图象，P点是距平衡位置‎2.5 cm的质点，图乙是Q点的振动图象．以下说法正确的是(　　)‎ A．0.05 s时质点Q具有最大的加速度和位移 B．0.05 s时质点P的速度正在减小，加速度正在增大 C．这列简谐横波的波速为‎15 m/s D．这列波的传播方向为＋x方向 E．从0.60 s到0.90 s，质点P通过的路程为‎30 cm 解析：选ACE.由图乙可知0.05 s时，Q质点在正向最大位移处，具有最大的加速度，A正确．由题给条件可画出0.05 s时波动图象如图所示：‎ 再由甲、乙两图分析可知波向x轴负方向传播，则可知此时质点P的速度在增大，加速度在减小，B、D错．由图甲知波长λ＝3 m，由图乙知周期T＝0.20 s，则波速v＝＝15 m/s，C正确．因Δt＝0.9 s－0.6 s＝0.3 s＝1.5T，则质点P通过的路程s＝1.5×4×5 cm＝30 cm，E正确．‎ ‎[综合应用题组]‎ ‎9．(多选)如图所示，空间同一平面内有A、B、C三点，AB＝‎5 m，BC＝‎4 m，AC＝‎3 m．A、C两点处有完全相同的波源做简谐运动，振动频率为1 360 Hz，波速为‎340 m/s.下列说法正确的是(　　)‎ A．B点的位移总是最大 B．A、B间有7个振动加强的点 C．两列波的波长均为‎0.25 m D．B、C间有12个振动减弱的点 E．振动减弱点的位移总是为零 解析：选CDE.波长λ＝＝ m＝0.25 m，B点到两波源的路程差Δx＝1 m＝4λ，该点为振动加强点，但不是位移总是最大，故A错误、C正确．AB上的点与A的距离和与C的距离之差一定小于AC，即小于3 m，则路程差可能为0、0.5 m、0.75 m、1 m、1.25 m、1.50 m、1.75 m、2 m、2.25 m、2.5 m、2.75 m，可知有11个振动加强点，故B错误．BC上的点与A的距离和与C的距离之差一定小于AC，即小于3 m，则路程差可能为0.125 m、0.375 m、0.625 m、0.875 m、1.125 m、1.375 m、1.625 m、1.875 m、2.125 m、2.375 m、2.625 m、2.875 m，有12个振动减弱点，故D正确．由于两波源的振幅相同，可知振动减弱点的位移总是为零，故E正确．‎ ‎10．(多选)如图所示，有一列减幅传播的简谐横波，x＝0与x＝‎75 m处的A、B两个质点的振动图象分别如图中实线与虚线所示．则这列波的(　　)‎ A．A点处波长是‎10 cm，B点处波长是‎5 cm B．周期一定都是2×10－2 s C．t＝0.012 5 s时刻，两质点的振动速度方向相反 D．传播速度一定是‎600 m/s E．A质点的振幅是B质点的振幅的2倍 解析：选BCE.由A、B两质点的振动图象可知两质点的周期均为2×10－2 s，所以B项正确；再由振动图象知t＝0时，质点A在平衡位置且向上振动，B处在波峰，则有75 m＝λ＋nλ(n＝0、1、2、3…)，解得λ＝(n＝0、1、2、3…)，所以A项错；在t＝0.012 5 s＝ T时，质点A向下振动，B向上振动，所以C项正确；波的传播速度v＝＝ m/s(n＝0、1、2、3…)．有多种可能，D项错；由图可知质点A的振幅为10 cm，质点B的振幅为5 cm，所以E项正确．‎ ‎11．在一列沿水平直线传播的简谐横波上有相距‎4 m的A、B两点，如图甲、乙分别是A、B两质点的振动图象，已知该波的波长大于‎2 m，求这列波可能的波速．‎ 解析：由振动图象得质点振动周期T＝0.4 s.‎ 若波由A向B传播，B点比A点晚振动的时间 Δt＝nT＋T(n＝0,1,2,3，…)，‎ 所以A、B间的距离为Δs＝nλ＋λ(n＝0,1,2,3，…)，‎ 则波长为λ＝＝(n＝0,1,2,3，…)．‎ 因为λ＞2 m，所以n＝0,1.‎ 当n＝0时，λ1＝ m，v1＝＝ m/s；‎ 当n＝1时，λ2＝ m，v2＝＝ m/s.‎ 若波由B向A传播，A点比B点晚振动的时间 Δt＝nT＋T(n＝0,1,2,3，…)，‎ 所以A、B间的距离为Δs＝nλ＋λ(n＝0,1,2,3，…)，‎ 则波长为λ＝＝(n＝0,1,2,3，…)．λ＞2 m，所以n＝0,1.‎ 当n＝0时，λ1＝16 m，v1＝40 m/s；‎ 当n＝1时，λ2＝ m，v2＝8 m/s.‎ 答案：若波由A向B传播，则波速为 m/s或者 m/s.若波由B向A传播，则波速为40 m/s或者8 m/s.‎ ‎12．如图所示，一列水平向右传播的简谐横波，波速大小为v＝‎0.6 m/s，P质点的平衡位置坐标为x＝‎0.96 m．从图中状态 计时(此时该波刚好传到距O点‎0.24 m的位置)，求：‎ ‎(1)经过多长时间，P质点第一次到达波峰？‎ ‎(2)经过多长时间，P质点第二次到达波谷？P质点第二次到达波谷时，P质点通过的路程及该时刻的位移为多少？‎ 解析：由波形图可知，波长λ＝0.24 m，振幅A＝5 cm，‎ 周期T＝＝＝0.4 s ‎(1)P质点第一次到达波峰所需的时间，就是初始时刻x＝‎0.06 m处的质点的振动状态传到P点所需的时间，由图可知：Δx1＝‎0.96 m－‎0.06 m＝‎‎0.90 m 则t1＝＝ s＝1.5 s ‎(2)为了求P质点第二次到达波谷所需的时间，可选取x＝‎0.18 m处的质点的振动状态作为研究对象，该振动状态传到P点所需的时间再加一个周期即为所求时间，则：‎ Δx2＝‎0.96 m－‎0.18 m＝‎‎0.78 m t2＝＋T＝ s＋0.4 s＝1.7 s 设波最右端传到P处所需时间为t3，有：‎ t3＝ s＝1.2 s 所以从质点P起振到第二次到达波谷历时 Δt＝t2－t3＝1.7 s－1.2 s＝0.5 s，相当于1T 所以P通过路程为 ‎5A‎＝‎‎0.25 m 此时刻质点P的位移为－5 cm 答案：(1)1.5 s　(2)1.7 s　0.25 m　－5 cm ‎第3节　光的折射　全反射 一、光的折射与折射率 ‎1．折射 光从一种介质斜射进入另一种介质时传播方向改变的现象．‎ ‎2．折射定律(如图) ‎ ‎(1)内容：折射光线与入射光线、法线处在同一平面内，折射光线与入射光线分别位于法线的两侧；入射角的正弦与折射角的正弦成正比．‎ ‎ (2)表达式：＝n12，式中n12是比例常数．‎ ‎(3)在光的折射现象中，光路是可逆的．‎ ‎3．折射率 ‎(1)定义：光从真空射入某种介质发生折射时，入射角的正弦与折射角的正弦的比值．‎ ‎(2)物理意义：折射率仅反映介质的光学特性，折射率大，说明光从真空射入到该介质时偏折大，反之偏折小．‎ ‎(3)定义式：n＝.不能说n与sin θ1成正比、与sin θ2成反比．折射率由介质本身的光学性质和光的频率决定．‎ ‎(4)计算公式：n＝，因v＜c，故任何介质的折射率总大于(填“大于”或“小于”)1.‎ ‎4．光密介质与光疏介质 ‎(1)光密介质：折射率较大的介质．‎ ‎(2)光疏介质：折射率较小的介质．‎ 二、全反射和光的色散现象 ‎1．全反射 ‎(1)条件：①光从光密介质射入光疏介质．‎ ‎②入射角≥临界角．‎ ‎(2)现象：折射光完全消失，只剩下反射光．‎ ‎(3)临界角：折射角等于90°时的入射角，用C表示，sin C＝.‎ ‎(4)应用：①全反射棱镜．‎ ‎②光导纤维，如图．‎ ‎2．光的色散 ‎(1)色散现象 白光通过三棱镜会形成由红到紫七种色光组成的彩色光谱，如图．‎ ‎(2)成因 由于n红＜n紫，所以以相同的入射角射到棱镜界面时，红光和紫光的折射角不同，就是说紫光偏折得更明显些，当它们射到另一个界面时，紫光的偏折角最大，红光偏折角最小．‎ ‎[自我诊断]‎ ‎1．判断正误 ‎(1)光的传播方向发生改变的现象叫光的折射．(×)‎ ‎(2)折射率跟折射角的正弦成正比．(×)‎ ‎(3)入射角足够大，也不一定能发生全反射．(√)‎ ‎(4)若光从空气中射入水中，它的传播速度一定增大．(×)‎ ‎(5)已知介质对某单色光的临界角为C，则该介质的折射率等于.(√)‎ ‎(6)密度大的介质一定是光密介质．(×)‎ ‎2．(多选)若某一介质的折射率较大，那么(　　)‎ A．光由空气射入该介质时折射角较大 B．光由空气射入该介质时折射角较小 C．光在该介质中的速度较大 D．光在该介质中的速度较小 解析：选BD.由＝n，且n＞1，可得sin θ2＝sin θ1，A错误，B正确；又因为n＝，得v＝c，C错误、D正确．‎ ‎3．(多选)如右图所示，一束光从空气中射向折射率为n＝的某种玻璃的表面，θ1表示入射角，则下列说法中正确的是(　　)‎ A．当θ1＞45°时会发生全反射现象 B．只有当θ1＝90°时才会发生全反射 C．无论入射角θ1是多大，折射角θ2都不会超过45°‎ D．欲使折射角θ2＝30°，应以θ1＝45°的角度入射 E．当入射角θ1＝arctan时，反射光线和折射光线恰好互相垂直 解析：选CDE.发生全反射现象的条件是：光从光密介质射向光疏介质，且入射角大于临界角，所以，选项A、B均错误；由折射率n＝＝可知，当入射角最大为90°时，折射角θ2＝45°，所以C正确；由折射率n＝可知，选项D、E均正确．‎ ‎4．一厚度为h的大平板玻璃水平放置，其下表面贴有一半径为r的圆形发光面．在玻璃板上表面放置一半径为R的圆纸片，圆纸片与圆形发光面的中心在同一竖直线上．已知圆纸片恰好能完全遮挡住从圆形发光面发出的光线(不考虑反射)，求平板玻璃的折射率．‎ 解析：根据全反射定律，圆形发光面边缘发出的光线射到玻璃板上表面时入射角为临界角(如图所示)设为θ，且sin θ＝.‎ 根据几何关系得：sin θ＝ 而L＝R－r，联立以上各式，解得n＝.‎ 答案： 考点一　光的折射率和折射定律 ‎1．对折射率的理解 ‎(1)折射率大小不仅反映了介质对光的折射本领，也反映了光在介质中传播速度的大小v＝.‎ ‎(2)折射率的大小不仅与介质本身有关，还与光的频率有关．同一种介质中，频率越大的色光折射率越大，传播速度越小．‎ ‎(3)同一种色光，在不同介质中虽然波速、波长不同，但频率相同．‎ ‎2．几种常见折射模型 类别 项目　　‎ 平行玻璃砖 三棱镜 圆柱体(球)‎ 光的折射图 通过平行玻璃砖的光线不改变传播方向，但要发生侧移 通过三棱镜的光线经两次折射后，出射光线向棱镜底边偏折 圆界面的法线是过圆心的直线，经过两次折射后向圆心偏折 应用 测定玻璃的折射率 全反射棱镜，改变光的传播方向 改变光的传播方向 ‎3．光路的可逆性 在光的折射现象中，光路是可逆的．如果让光线逆着原来的折射光线射到界面上，光线就会逆着原来的入射光线发生折射．‎ ‎1．(多选)如图所示，真空中有一个半径为R、质量分布均匀的玻璃球，频率为f的激光束在真空中沿直线BC传播，于C点经折射进入玻璃球，并在玻璃球表面的D点又经折射进入真空中．已知∠COD＝120°，玻璃球对该激光束的折射率为，则下列说法中正确的是(设c为真空中的光速)(　　)‎ A．激光束的入射角α＝60°‎ B．改变入射角α的大小，激光束可能在玻璃球的内表面发生全反射 C．激光束在射入玻璃球后，光的频率变小 D．此激光束在玻璃中的波长为λ＝ E．从C点射入玻璃球的激光束，在玻璃球中不经反射传播的最长时间为 解析：选ADE.由几何知识得到激光束在C点的折射角r＝30°，由n＝得，sin α＝nsin r＝，得α＝60°，故A正确．激光束从C点进入玻璃球时，无论怎样改变入射角α，在D点的入射角等于C点的折射角，根据光路可逆性原理得知，光束不可能在D点发生全反射，一定能从D点折射出玻璃球，故B错误．‎ 光的频率由光源决定，则激光束穿越玻璃球时频率不变，选项C错误．激光束在玻璃球中传播的速度为v＝＝，由v＝λf得λ＝，选项D正确．当光束沿玻璃球直径方向射入，路程最长，传播时间最长为t＝，可得t＝，选项E正确．‎ ‎2．(2017·湖北武汉调研)如图所示，厚度为d的平行玻璃砖与光屏EF均竖直放置，玻璃砖右侧面距光屏为d，左侧面距激光源S也是d.由S发出的两束激光，一束垂直玻璃砖表面，另一束与玻璃砖表面成45°角，两束光经折射后射到光屏上，光屏上两光点间距为d，已知光在真空中的传播速度为c.求：‎ ‎(1)玻璃砖的折射率；‎ ‎(2)激光在玻璃砖中传播的时间．‎ 解析：(1)作出光路图如图所示，入射角α＝45°‎ 设折射角为β，光束从玻璃砖出射时偏离入射点距离为y，y＝d sin β＝＝ 由折射定律n＝＝ ‎(2)n＝， ＝vt 解得t＝ 答案：(1)　(2) ‎3．(2016·高考全国丙卷)如图，玻璃球冠的折射率为，其底面镀银，底面的半径是球半径的倍；在过球心O且垂直于底面的平面(纸面)内，有一与底面垂直的光线射到玻璃球冠上的M点，该光线的延长线恰好过底面边缘上的A点，求该光线从球面射出的方向相对于其初始入射方向的偏角．‎ 解析：设球半径为R，球冠底面中心为O′，连接OO′，则OO′⊥AB.令∠OAO′＝α，有cos α＝＝①‎ 即α＝30°②‎ 由题意知MA⊥AB 所以∠OAM＝60°③‎ 设图中N点为光线在球冠内底面上的反射点，所考虑的光线的光路图如图所示．设光线在M点的入射角为i，折射角为r，在N点的入射角为i′，反射角为i″，玻璃的折射率为n.由于△OAM为等边三角形，有i＝60°④‎ 由折射定律有sin i＝nsin r⑤‎ 代入题给条件n＝得r＝30°⑥‎ 作底面在N点的法线NE，‎ 由于NE∥AM，有i′＝30° ⑦‎ 根据反射定律，有i″＝30°⑧‎ 连接ON，由几何关系知△MAN≌△MON，故有∠MNO＝60°⑨‎ 由⑦⑨式得∠ENO＝30°⑩‎ 于是∠ENO为反射角，ON为反射光线．这一反射光线经球面再次折射后不改变方向．所以，射出玻璃球冠的光线相对于入射光线的偏角β为 β＝180°－∠ENO＝150°⑪‎ 答案：150°‎ 应用光的折射定律解题的一般思路 ‎(1)根据入射角、折射角及反射角之间的关系．作出比较完整的光路图．‎ ‎(2)充分利用光路图中的几何关系，确定各角之间的联系，根据折射定律求解相关的物理量：折射角、折射率等．‎ ‎(3)注意在折射现象中，光路是可逆的．‎ 考点二　光的全反射的理解及应用 ‎1．求解光的折射、全反射问题的四点提醒 ‎(1)光密介质和光疏介质是相对而言的．同一种介质，相对于其他不同的介质，可能是光密介质，也可能是光疏介质．‎ ‎(2)如果光线从光疏介质进入光密介质，则无论入射角多大，都不会发生全反射现象．‎ ‎(3)在光的反射和全反射现象中，均遵循光的反射定律，光路均是可逆的．‎ ‎(4)当光射到两种介质的界面上时，往往同时发生光的折射和反射现象，但在全反射现象中，只发生反射，不发生折射．‎ ‎2．求解全反射现象中光的传播时间的一般思路 ‎(1)全反射现象中，光在同种均匀介质中的传播速度不发生变化，即v＝.‎ ‎(2)全反射现象中，光的传播路程应结合光路图与几何关系进行确定．‎ ‎(3)利用t＝求解光的传播时间．‎ ‎3．解决全反射问题的一般方法 ‎(1)确定光是从光密介质进入光疏介质．‎ ‎(2)应用sin C＝确定临界角．‎ ‎(3)根据题设条件，判定光在传播时是否发生全反射．‎ ‎(4)如发生全反射，画出入射角等于临界角时的临界光路图．‎ ‎(5)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算，解决问题．‎ ‎[典例]　(2016·高考全国乙卷)如图，在注满水的游泳池的池底有一点光源A，它到池边的水平距离为‎3.0 m．从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角，水的折射率为.‎ ‎(1)求池内的水深；‎ ‎(2)一救生员坐在离池边不远处的高凳上，他的眼睛到池面的高度为‎2.0 m．当他看到正前下方的点光源A时，他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字)．‎ 解析　(1)如图，设到达池边的光线的入射角为i，依题意，水的折射率n＝，光线的折射角θ＝90°.由折射定律有 nsin i＝sin θ①‎ 由几何关系有 sin i＝②‎ 式中，l＝3.0 m，h是池内水的深度．联立①②式并代入题给数据得 h＝ m≈‎2.6 m③‎ ‎(2)设此时救生员的眼睛到池边的距离为x ‎.依题意，救生员的视线与竖直方向的夹角为θ′＝45°.由折射定律有nsin i′＝sin θ′④‎ 式中，i′是光线在水面的入射角．设池底点光源A到水面入射点的水平距离为a.由几何关系有 sin i′＝⑤‎ x＋l＝a＋h′⑥‎ 式中h′＝2 m．联立③④⑤⑥式得 x＝ m≈‎0.7 m⑦‎ 答案　(1)2.6 m　(2)0.7 m ‎(1)几何光学一定要注意几何关系的应用，关键是要根据题意，画出正确的光路图，根据光路图找出需要的各种几何关系，比如本题中的sin i＝、sin i′＝、x＋l＝a＋h′等．‎ ‎(2)利用好光路图中的临界光线，准确地判断出恰好发生全反射的光路图是解题的关键，且在作光路图时尽量与实际相符．‎ ‎1．(2017·河北衡水中学调研)(多选)如图所示，一块上、下表面平行的玻璃砖的厚度为L，玻璃砖的折射率n＝ ，若光从上表面AB射入的入射角i＝60°，光在真空中的光速为c，则(　　)‎ A．折射角r＝30°‎ B．光在玻璃中传播的时间为 C．光在玻璃中传播的时间为 D．改变入射角i，光在下表面CD可能发生全发射 解析：选AC.由n＝得sin r＝＝＝0.5，得r＝30°，故A正确；光在玻璃中传播的速度为v＝，由几何知识可知光在玻璃中传播的路程为s＝，则光在玻璃中传播的时间为t＝＝＝＝，故B错误，C正确；由于光在CD面上的入射角等于光在AB面上的折射角，根据光路可逆性原理可知光一定能从CD面射出，故D错误．‎ ‎2．半径为R、介质折射率为n的透明圆柱体，过其轴线OO′的截面如图所示．位于截面所在的平面内的一细束光线，以角i0由O点入射，折射光线由上边界的A点射出．当光线在O点的入射角减小至某一值时，折射光线在上边界的B点恰好发生全反射．求A、B两点间的距离．‎ 解析：当光线在O点的入射角为i0时，设折射角为r0，由折射定律得 ＝n①‎ 设A点与左端面的距离为dA，由几何关系得 sin r0＝②‎ 若折射光线恰好发生全反射，则在B点的入射角恰好为临界角C，设B点与左端面的距离为dB，由折射定律得 sin C＝③‎ 由几何关系得sin C＝④‎ 设A、B两点间的距离为d，可得 d＝dB－dA⑤‎ 联立①②③④⑤式得 d＝R⑥‎ 答案：R ‎3．(2017·贵州遵义模拟)如图所示，一个足够大的水池盛满清水，水深h＝‎4 m，水池底部中心有一点光源A，其中一条光线斜射到水面上距A为l＝‎5 m的B点时，它的反射光线与折射光线恰好垂直．‎ ‎(1)求水的折射率n；‎ ‎(2)用折射率n和水深h表示水面上被光源照亮部分的面积(圆周率用π表示)．‎ 解析：(1)设射向B点的光线入射角与折射角分别为i和r，由题意得sin i＝，i＋r＝90°，‎ 故水的折射率为n＝＝＝1.33.‎ ‎(2)设射向水面的光发生全反射的临界角为C，‎ 则有sin C＝，‎ 圆形光斑的半径为R＝htan C，‎ 圆形光斑的面积为S＝πR2，‎ 联立可解得S＝.‎ 答案：(1)1.33　(2) ‎4．一个半圆柱形玻璃砖，其横截面是半径为R的半圆，AB为半圆的直径，O为圆心，如图所示．玻璃的折射率为n＝.‎ ‎(1)一束平行光垂直射向玻璃砖的下表面，若光线到达上表面后，都能从该表面射出，则入射光束在AB上的最大宽度为多少？‎ ‎(2)一细束光线在O点左侧与O相距R处垂直于AB从下方入射，求此光线从玻璃砖射出点的位置．‎ 解析：(1)在O点左侧，设从E点射入的光线进入玻璃砖后在上表面的入射角恰好等于全反射的临界角θ，则OE区域的入射光线经上表面折射后都能从玻璃砖射出，如图，由全反射条件有sin θ＝①‎ 由几何关系有OE＝Rsin θ②‎ 由对称性可知，若光线都能从上表面射出，光束的宽度最大为l＝2OE③‎ 联立①②③式，代入已知数据得l＝R④‎ ‎(2)设光线在距O点R的C点射入后，在上表面的入射角为α，由几何关系及①式和已知条件得 α＝60°>θ⑤‎ 光线在玻璃砖内会发生三次全反射，最后由G点射出，如图，由反射定律和几何关系得 OG＝OC＝R⑥　‎ 射到G点的光有一部分被反射，‎ 沿原路返回到达C点射出．‎ 答案：(1)R　(2)光线从G点射出时，OG＝OC＝R，射到G点的光有一部分被反射，沿原路返回到达C点射出 考点三　实验：测定玻璃的折射率 ‎1．实验原理：用插针法找出与入射光线AO对应的出射光线O′B，确定出O′点，画出折射光线OO′，然后测量出角θ1和θ2，代入公式计算玻璃的折射率．‎ ‎2．实验器材：白纸、图钉、大头针、直尺、铅笔、量角器、平木板、长方形玻璃砖．‎ ‎3．实验过程：‎ ‎(1)铺白纸、画线．‎ ‎①如图所示，将白纸用图钉按在平木板上，先在白纸上画出一条直线aa′作为界面，过aa′上的一点O画出界面的法线MN，并画一条线段AO作为入射光线．‎ ‎②把玻璃砖平放在白纸上，使它的长边跟aa′对齐，画出玻璃砖的另一条长边bb′.‎ ‎(2)插针与测量．‎ ‎①在线段AO上竖直地插上两枚大头针P1、P2，透过玻璃砖观察大头针P1、P2的像，调整视线的方向，直到P1的像被P2挡住，再在观察的这一侧依次插两枚大头针P3、P4，使P3挡住P1、P2的像，P4挡住P1、P2的像及P3，记下P3、P4的位置．‎ ‎②移去玻璃砖，连接P3、P4并延长交bb′于O′，连接OO′即为折射光线，入射角θ1＝∠AOM，折射角θ2＝∠O′ON.‎ ‎③用量角器测出入射角和折射角，查出它们的正弦值，将数据填入表格中．‎ ‎④改变入射角θ1，重复实验步骤，列表记录相关测量数据．‎ ‎4．数据处理：计算每次的折射率n，求出平均值.‎ ‎5．注意事项 ‎(1)玻璃砖应选用厚度、宽度较大的．‎ ‎(2)大头针要插得竖直，且间隔要大些．‎ ‎(3)入射角不宜过大或过小，一般在15°～75°之间．‎ ‎(4)玻璃砖的折射面要画准，不能用玻璃砖界面代替直尺画界线．‎ ‎(5)实验过程中，玻璃砖和白纸的相对位置不能改变．‎ ‎1．用三棱镜做测定玻璃折射率的实验，先在白纸上放好三棱镜，在棱镜的一侧插入两枚大头针P1和P2，然后在棱镜的另一侧观察，调整视线使P1的像被P2的像挡住，接着在眼睛所在的一侧插两枚大头针P3、P4，使P3挡住P1、P2的像，P4挡住P3和P1、P2的像，在纸上标出的大头针位置和三棱镜轮廓如图所示．‎ ‎(1)在图上画出所需的光路．‎ ‎(2)为了测出棱镜玻璃的折射率，需要测量的量是__________，在图上标出它们．‎ ‎(3)计算折射率的公式是__________________．‎ 解析：(1)如图所示，画出通过P1、P2的入射光线，交AC面于O，画出通过P3、P4的出射光线交AB面于O′，则光线OO′就是入射光线P1P2在三棱镜中的折射光线．‎ ‎(2)在所画的图上注明入射角θ1和折射角θ2，并画出虚线部分，用量角器量出θ1和θ2(或用直尺测出线段EF、OE、GH、OG的长度)．‎ ‎(3)根据折射率的定义可知n＝ sin θ2＝，则n＝＝.‎ 答案：(1)见解析　(2)θ1和θ2(或线段EF、OE、GH、OG的长度)　(3)n＝ ‎2．在“测定玻璃的折射率”的实验中，某同学经正确的操作，插好了4枚大头针P1、P2和P3、P4，如图所示．‎ ‎(1)在坐标线上画出完整的光路图，并标出入射角θ1和折射角θ2.‎ ‎(2)对你画出的光路图进行测量，求出该玻璃的折射率n＝________(结果保留2位有效数字)．‎ 解析：(1)过P1、P2作直线与玻璃砖长表面交于O点，过O点作长表面的垂线EF，即为过O点的法线；过P3、P4作直线与玻璃砖短表面交于O′点，过O′点作短表面的垂线MN，即为过O′点的法线；连接O、O′两点；从P1到P4在三段线段上依次标出方向．如图所示．‎ ‎(2)根据图可知 sin θ1＝＝ sin θ2＝＝ 根据折射率公式得n＝＝＝＝1.4‎ 答案：(1)见解析　(2)1.4‎ ‎3．(2016·福建晋江联考)在“测定玻璃折射率”的实验中，如图所示为所插四枚大头针的位置，aa′为事先确定好的玻璃砖的其中一平行边，bb′为准确操作时应画出的玻璃砖的另一平行边．‎ ‎(1)如果在实验过程中不小心将玻璃砖向上平移了一些，bb′移到图中虚线①位置，而在作光路图时aa′不变，则所测得的折射率将________(填“偏大”“偏小”或“不变”)；‎ ‎(2)若所使用的玻璃砖的bb′边与aa′不平行(如图虚线②所示)，其他操作无误，则所测得的折射率将________(填“偏大”“偏小”或“不变”)．‎ 解析：(1)如果在实验过程中不小心将玻璃砖向上平移了一些，bb′移到图中虚线①位置，而在作光路图时aa′不变，作出光路图如图所示，测量得到的入射角没有变化，而折射角偏小，根据折射率公式n＝可知，所测得的折射率将偏大．‎ ‎(2)测折射率时，只要操作正确，与玻璃砖形状无关．所以若所使用的玻璃砖的bb′边与aa′不平行，其他操作无误，则所测得的折射率将不变．‎ ‎ 答案：(1)偏大　(2)不变 课时规范训练 ‎[基础巩固题组]‎ ‎1．(多选)已知介质对某单色光的临界角为θ，则(　　)‎ A．该介质对此单色光的折射率为 B．此单色光在该介质中传播速度为csin θ(c为真空中光速)‎ C．此单色光在该介质中的波长是真空中波长的sin θ倍 D．此单色光在该介质中的频率是真空中的 解析：选ABC.介质对该单色光的临界角为θ，它的折射率n＝，A正确；此单色光在介质中的传播速度v＝＝csin θ，B正确；波长λ＝＝＝λ0sin θ，C正确；光的频率是由光源决定的，与介质无关，D错误．‎ ‎2．如图，一束光经玻璃三棱镜折射后分为两束单色光a、b，波长分别为λa、λb，该玻璃对单色光a、b的折射率分别为na、nb，则(　　)‎ A．λa＜λb，na＞nb B．λa＞λb，na＜nb C．λa＜λb，na＜nb D．λa＞λb，na＞nb 解析：选B.由题图可知，在入射角相同的情况下，光线a的偏折程度小于光线b的偏折程度，因此光线a的折射率小于光线b的折射率，故选项A、D错误；由于折射率越大频率越高，因此光线a的频率小于光线b的频率，由c＝λν可知光线a的波长大于光线b的波长，选项B正确．‎ ‎3．某同学通过实验测定半圆形玻璃砖的折射率n.如图甲所示，O是圆心，MN是法线，AO、BO 分别表示某次测量时光线在空气和玻璃砖中的传播路径．该同学测得多组入射角i和折射角r，作出sin i－sin r图象如图乙所示．则(　　)‎ A．光由A经O到B，n＝1.5‎ B．光由B经O到A，n＝1.5‎ C．光由A经O到B，n＝0.67‎ D．光由B经O到A，n＝0.67‎ 解析：选B.光线从空气斜射入介质时，入射角大于折射角，从题图可以看出对应的折射角比入射角大，故光是从介质射入空气中，即光由B经O到A，由sin i－sin r图象的斜率表示折射率的倒数，可得n＝＝1.5，选项B正确．‎ ‎4．光纤通信中信号传播的主要载体是光导纤维，它的结构如图所示，其内芯和外套材料不同，光在内芯中传播．下列关于光导纤维的说法中正确的是(　　)‎ A．内芯的折射率比外套的大，光传播时在内芯与外套的界面上发生全反射 B．内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生全反射 C．波长越短的光在光纤中传播的速度越大 D．频率越大的光在光纤中传播的速度越大 解析：选A.光纤内芯比外套折射率大，在内芯与外套的界面上发生全反射，A对，B错；频率大的光，波长短，折射率大，在光纤中传播速度小，C、D错．‎ ‎5．打磨某剖面如图所示的宝石时，必须将OP、OQ边与轴线的夹角θ切磨在θ1<θ<θ2的范围内，才能使从MN边垂直入射的光线，在OP边和OQ边都发生全反射(仅考虑如图所示的光线第一次射到OP边并反射到OQ边后射向MN边的情况)，则下列判断正确的是(　　)‎ A．若θ>θ2，光线一定在OP边发生全反射 B．若θ>θ2，光线会从OQ边射出 C．若θ<θ1，光线会从OP边射出 D．若θ<θ1，光线会在OP边发生全反射 解析：选D.光线发生全反射的条件是光从光密介质进入光疏介质时，入射角i大于临界角C.光线从图示位置入射，到达OP边时入射角i1＝－θ，θ越小，i1越大，发生全发射的可能性越大，根据题意，要在OP边上发生全反射，应满足θ＜θ2，A、B错误．若光线在OP上发生全反射后到达OQ边，入射角i2＝3θ－，θ越大，i2越大， 发生全反射的可能性越大，根据题意，要在OQ边上发生全反射，应满足θ＞θ1，C错误、D正确．‎ ‎6．某研究性学习小组利用插针法测量半圆形玻璃砖的折射率．实验探究方案如下：在白纸上作一直线MN，并作出它的一条垂线AB，将半圆形玻璃砖(底面的圆心为O)放在白纸上，它的直径与直线MN重合，在垂线AB上插两枚大头针P1和P2，然后在半圆形玻璃砖的右侧插上适量的大头针，可以确定光线P1P2通过玻璃砖后的光路，从而求出玻璃砖的折射率．实验中提供的器材除了半圆形玻璃砖、木板和大头针外，还有量角器等．‎ ‎(1)某同学用上述方法测量玻璃砖的折射率，他在画出的垂线AB上竖直插上了P1、P2两枚大头针，但在半圆形玻璃砖的右侧区域内，不管眼睛在何处，都无法透过玻璃砖同时看到P1、P2的像，原因是________________________.‎ 为同时看到P1、P2的像，他应采取的措施是_______________________.‎ ‎(2)在采取相应措施后，请在半圆形玻璃砖的右侧画出所插大头针的可能位置，并用“×”表示，作出光路图．‎ ‎(3)为计算折射率，将应测量的物理量标注在光路图上，并由此得出折射率的计算公式为n＝________.‎ 解析：(1)在半圆形玻璃砖的右侧区域内，不管眼睛在何处，都无法透过玻璃砖同时看到P1、P2的像，原因是入射光线AB离圆心较远，在半圆形面发生了全反射；为同时看到P1、P2的像，‎ 他应采取的措施是：沿着MN方向，向M点方向平移玻璃砖．‎ ‎(2)光路如右图所示．‎ ‎(3)折射率的计算公式为n＝.‎ 答案：(1)入射光线AB离圆心较远，在半圆形面发生了全反射　沿着MN方向向M点方向平移玻璃砖　(2)见解析　(3)见解析　 ‎7．如图所示，AOB是截面为扇形的玻璃砖的横截面图，其顶角θ＝76°，今有一细束单色光在横截面内从OA边上的点E沿垂直于OA的方向射入玻璃砖，光线直接到达AB面且恰好未从AB面射出．已知OE＝OA，cos 53°＝0.6，试求：‎ ‎(1)玻璃砖的折射率n；‎ ‎(2)光线第一次从OB射出时折射角的正弦值．‎ 解析：(1)因OE＝OA，由数学知识知光线在AB面的入射角等于37°，光线恰好未从AB面射出，所以AB面入射角等于临界角，则临界角为C＝37°.‎ 由sin C＝得n＝.‎ ‎(2)据几何知识得β＝θ＝76°，则OB面入射角为 α＝180°－‎2C－β＝30°.‎ 设光线第一次从OB射出的折射角为r，‎ 由＝n得sin r＝.‎ 答案：(1)　(2) ‎[综合应用题组]‎ ‎8．如图所示，直角三角形ABC是一玻璃砖的横截面，AB＝L，∠C＝90°，∠A＝60°.一束单色光PD从AB边上的D点射入玻璃砖，入射角为45°，DB＝，折射光DE恰好射到玻璃砖BC边的中点E，已知光在真空中的传播速度为c.求：‎ ‎(1)玻璃砖的折射率；‎ ‎(2)该光束从AB边上的D点射入玻璃砖到第一次射出玻璃砖所需的时间．‎ 解析：(1)作出光路图，如图所示，过E点的法线是三角形的中位线，由几何关系可知△DEB为等腰三角形，故DE＝DB＝.‎ 由几何知识知光在AB边折射时折射角为30°，所以 n＝＝ .‎ ‎(2)设临界角为θ，有sin θ＝，可解得θ＝45°，由光路图及几何知识可判断，光在BC边发生全反射，在AC边第一次射出玻璃砖．‎ 根据几何知识可知EF＝，则光束从AB边射入玻璃砖到第一次射出玻璃砖所需要的时间t＝.代入v＝可解得t＝.‎ 答案：(1)　(2).‎ ‎9．半径为R的固定半圆玻璃砖的横截面如图所示，O点为圆心，OO′与直径AB垂直，足够大的光屏CD紧靠在玻璃砖的左侧且与AB垂直，一光束沿半径方向与OO′成θ＝30°射向O点，光屏CD区域出现两个光斑，已知玻璃的折射率为.求：‎ ‎(1)当θ变为多大时，两光斑恰好变为一个；‎ ‎(2)当光束沿半径方向与OO′成θ＝30°射向O点时，光屏CD区域两个光斑的距离．‎ 解析：(1)光屏上的两个光斑恰好变为一个，说明光线恰好在AB面发生全反射，n＝ 代入数据可得θ＝45°‎ ‎(2)当θ＝30°时，如图所示光线在AB面同时发生反射和折射，反射光线沿半径射出到P点，α＝θ＝30°‎ 可得＝Rcot α＝R 在AB面发生折射，由n＝ 解得sin β＝，β＝45°‎ 可得＝R 则两光斑间距离 ＝＋＝(＋1)R 答案：(1)45°　(2)(＋1)R ‎10．一玻璃立方体中心有一点状光源．今在立方体的部分表面镀上不透明薄膜，以致从光源发出的光线只经过一次折射不能透出立方体．已知该玻璃的折射率为，求镀膜的面积与立方体表面积之比的最小值．‎ 解析：光源发出的光线只经过一次折射不能透出立方体，表示光线第一次到达表面时发生全反射的区域不需要镀膜，发生非全反射的区域需要镀膜．‎ 考虑从玻璃立方体中心O点发出一条光线，假设它斜射到玻璃立方体上表面发生折射，由折射定律可知 nsin θ＝sin α①‎ 式中，n为折射率，θ为入射角，α为折射角．‎ 现假设A点是上表面面积最小的不透明薄膜边缘上的一点．‎ 由题意，在A点恰好发生全反射，故αA＝②‎ 如图所示，设线段OA在立方体上表面的投影长为RA，由几何关系有 sin θA＝③‎ 式中a为玻璃立方体的边长．‎ 由①②③式，并代入数据得RA＝＝④‎ 由题意，上表面所镀面积最小的不透明薄膜应是半径为RA的圆，所求的镀膜面积S′与玻璃立方体的表面积S之比＝⑤‎ 由④⑤两式得＝ 答案： 第4节　光的波动性、电磁波、相对论 一、光的干涉 ‎1．定义 在两列光波的叠加区域，某些区域的光被加强，出现亮纹，某些区域的光被减弱，出现暗纹，且加强和减弱互相间隔的现象叫做光的干涉现象．‎ ‎2．条件 两列光的频率相等，且具有恒定的相位差，才能产生稳定的干涉现象．‎ ‎3．双缝干涉 由同一光源发出的光经双缝后形成两束振动情况总是相同的相干光波，屏上某点到双缝的路程差是波长的整数倍处出现亮条纹；路程差是半波长的奇数倍处出现暗条纹．相邻的明条纹(或暗条纹)之间距离Δx与波长λ、双缝间距d及屏到双缝距离l的关系为Δx＝λ.‎ ‎4．薄膜干涉 利用薄膜(如肥皂液薄膜)前后表面反射的光相遇而形成的．图样中同一条亮(或暗)条纹上所对应薄膜厚度相同．‎ 二、光的衍射 ‎1．光的衍射现象 光在遇到障碍物时，偏离直线传播方向而照射到阴影区域的现象叫做光的衍射．‎ ‎2．光发生明显衍射现象的条件 当孔或障碍物的尺寸比光波波长小，或者跟光波波长相差不多时，光才能发生明显的衍射现象．‎ ‎3．衍射图样 ‎(1)单缝衍射：中央为亮条纹，向两侧有明暗相间的条纹，但间距和亮度不同．白光衍射时，中央仍为白光，最靠近中央的是紫光，最远离中央的是红光．‎ ‎(2)圆孔衍射：明暗相间的不等距圆环．‎ ‎(3)泊松亮斑：光照射到一个半径很小的圆板后，在圆板的阴影中心出现的亮斑，这是光能发生衍射的有力证据之一．‎ 三、光的偏振 ‎1．偏振光：在跟光传播方向垂直的平面内，光振动在某一方向较强而在另一些方向较弱的光即为偏振光．‎ 光的偏振现象证明光是横波(填“横波”或“纵波”)．‎ ‎2．自然光：太阳、电灯等普通光源发出的光，包括在垂直于传播方向上沿各个方向振动的光，而且沿各个方向振动的光波的强度都相同，这种光叫做自然光．‎ ‎3．偏振光的产生 通过两个共轴的偏振片观察自然光，第一个偏振片的作用是把自然光变成偏振光，叫做起偏器．第二个偏振片的作用是检验光是否是偏振光，叫做检偏器．‎ 四、电磁场和电磁波 ‎1．电磁波的产生 ‎(1)麦克斯韦电磁场理论 变化的磁场产生电场，变化的电场产生磁场．‎ ‎(2)电磁场 变化的电场和变化的磁场总是相互联系成为一个完整的整体，这就是电磁场．‎ ‎(3)电磁波 电磁场(电磁能量)由近及远地向周围传播形成电磁波．‎ ‎①电磁波是横波，在空间传播不需要介质；‎ ‎②真空中电磁波的速度为3×108 m/s；‎ ‎③v＝λf对电磁波同样适用；‎ ‎④电磁波能产生反射、折射、干涉和衍射等现象．‎ ‎2．电磁波的发射和接收 ‎(1)发射电磁波的条件 ‎①要有足够高的振荡频率；‎ ‎②电路必须开放，使振荡电路的电场和磁场分散到尽可能大的空间．‎ ‎(2)调制有调幅和调频两种方式，解调是调制的逆过程．‎ ‎(3)电磁波谱 ‎①定义：按电磁波的波长从长到短分布是无线电波、红外线、可见光、紫外线、X射线和γ射线，形成电磁波谱；‎ ‎②电磁波谱的特性、应用 电磁 波谱 频率 ‎/Hz 真空中 波长/m 特性 应用 递变 规律 无线 电波 ‎＜3×‎ ‎1011‎ ‎＞10－3‎ 波动性强，‎ 易发生衍射 无线电技术 红外线 ‎1011～‎ ‎1015‎ ‎10－3～‎ ‎10－7‎ 热效应 红外线 遥感 可见光 ‎1015‎ ‎10－7‎ 引起视觉 照明、摄影 紫外线 ‎1015～‎ ‎1017‎ ‎10－7～‎ ‎10－9‎ 化学效应、‎ 荧光效应、‎ 能杀菌 医用消毒、‎ 防伪 X射线 ‎1016～‎ ‎1019‎ ‎10－8～‎ ‎10－11‎ 贯穿性强 检查、医用 透视 γ射线 ‎＞1019‎ ‎＜10－11‎ 贯穿本领 最强 工业探伤、‎ 医用治疗 五、相对论 ‎1．狭义相对论的两个基本假设 ‎(1)狭义相对性原理：在不同的惯性参考系中，一切物理规律都是相同的．‎ ‎(2)光速不变原理：真空中的光速在不同的惯性参考系中都是相同的．‎ ‎2．时间和空间的相对性 ‎“同时”的相对性：同时是相对的，与参考系的运动有关．‎ ‎[自我诊断]‎ ‎1．判断正误 ‎(1)光的颜色由光的频率决定．(√)‎ ‎(2)只有频率相同的两列光波才有可能产生稳定的干涉．(√)‎ ‎(3)在双缝干涉实验中，双缝的作用是使白光变成单色光．(×)‎ ‎(4)阳光下茂密的树荫中地面上的圆形亮斑是光的衍射形成的．(×)‎ ‎(5)自然光是偏振光．(×)‎ ‎(6)电场周围一定存在磁场，磁场周围一定存在电场．(×)‎ ‎(7)无线电波不能发生干涉和衍射现象．(×)‎ ‎(8)波长不同的电磁波在本质上完全不同．(×)‎ ‎(9)真空中的光速在不同惯性参考系中是不同的．(×)‎ ‎2．(2016·湖北联考)(多选)关于波的现象，下列说法正确的有(　　)‎ A．当波从一种介质进入另一种介质时，频率不会发生变化 B．光波从空气进入水中后，更容易发生衍射 C．波源沿直线匀速靠近一静止接收者，则接收者接收到波信号的频率会比波源频率低 D．不论机械波、电磁波，都满足v＝λf，式中三参量依次为波速、波长、频率 E．电磁波具有偏振现象 解析：选ADE.由波的性质可知，A正确；光波从空气进入水中，波速变小，波长变短，故不容易发生衍射，B错；由多普勒效应可判断，波源靠近接收者的过程中，接收者接收到波信号的频率会比波源频率高，则C错误；波速的计算公式v＝λf(v波速，λ波长，f频率)对机械波和电磁波通用，则D正确；光波具有偏振现象，光波是电磁波，则E正确．‎ ‎3．(多选)以下说法中正确的是(　　)‎ A．对于同一障碍物，波长越大的光波越容易绕过去 B．白光通过三棱镜在屏上出现彩色条纹是光的一种干涉现象 C．红光由空气进入水中，波长变长、颜色不变 D．用透明的标准样板和单色光检查平面的平整度是利用了光的干涉 E．不管光源与观察者是否存在相对运动，观察者观察到的光速是不变的 解析：选ADE.波长越长的光越容易发生衍射现象，故越容易绕过障碍物，所以A正确；白光通过三棱镜在屏上出现彩色条纹是光的一种折射现象，所以B错误；红光由空气进入水中，频率不变，故颜色不变，传播速度减小，故波长变短，所以C错误；用透明的标准样板和单色光检查平面的平整度是利用了光的干涉，即薄膜干涉，所以D正确；根据狭义相对性原理，不管光源与观察者是否存在相对运动，观察者观察到的光速是不变的，故E正确．‎ ‎4．在观察光的双缝干涉现象的实验中：‎ ‎(1)将激光束照在如图乙所示的双缝上，在光屏上观察到的现象是图甲中的________．‎ ‎(2)换用两缝间距离更小的双缝，保持双缝到光屏的距离不变，在光屏上观察到的条纹宽度将________；保持双缝间距离不变，减小光屏到双缝的距离，在光屏上观察到的条纹宽度将________．(以上均选填“变宽”“变窄”或“不变”)‎ 解析：(1)双缝干涉图样是平行且等宽的明暗相同的条纹，A图正确．‎ ‎(2)根据Δx＝λ知，双缝间的距离d减小时，条纹间距变宽；双缝到屏的距离l减小时，条纹间距变窄．‎ ‎ 答案：(1)A　(2)变宽　变窄 考点一　光的干涉、衍射及偏振 ‎1．单缝衍射与双缝干涉的比较 ‎2.自然光和偏振光的比较 自然光(非偏振光)‎ 偏振光 光的来源 直接从光源发出的光 自然光通过起偏器后的光 光的振动方向 在垂直于光的传播方向的平面内，光振动沿任意方向，且沿各个方向振动的光的强度相同 在垂直于光的传播方向的平面内，光振动沿特定方向 ‎1．(2017·北京丰台区一模)如图所示的4种明暗相间的条纹分别是红光、蓝光各自通过同一个双缝干涉仪器形成的干涉图样以及黄光、紫光各自通过同一个单缝形成的衍射图样(黑色部分表示亮纹)．在下面的4幅图中从左往右排列，亮条纹的颜色依次是(　　)‎ A．红黄蓝紫　　　 B．红紫蓝黄 C．蓝紫红黄 D．蓝黄红紫 解析：选B.双缝干涉条纹是等间距的，而单缝衍射条纹除中央亮条纹最宽最亮之外，两侧条纹亮度、宽度都逐渐减小，因此a、c为双缝干涉条纹，b、d为单缝衍射条纹．双缝干涉条纹的宽度(即相邻明、暗条纹间距)Δx＝λ ‎，红光波长比蓝光波长长，则红光干涉条纹间距大于蓝光干涉条纹间距，即a、c分别对应于红光和蓝光．而在单缝衍射中，当单缝宽度一定时，波长越长，衍射越明显，即中央条纹越宽越亮，b、d分别对应于紫光和黄光．综上所述，a、b、c、d四个图中亮条纹的颜色依次是：红、紫、蓝、黄，B正确．‎ ‎2．(多选)如图所示，偏振片P的透振方向(用带有箭头的实线表示)为竖直方向．下列四种入射光束中，能在P的另一侧观察到透射光的是(　　)‎ A．太阳光 B．沿竖直方向振动的光 C．沿水平方向振动的光 D．沿与竖直方向成45°角振动的光 解析：选ABD.偏振片只让沿某一方向振动的光通过，当偏振片的透振方向与光的振动方向不同时，透射光的强度不同，它们平行时最强，而垂直时光不能透过偏振片．太阳光是自然光，光波可沿任何方向振动，所以在P的另一侧能观察到透射光；沿竖直方向振动的光，振动方向与偏振片的透振方向相同，当然可以看到透射光；沿水平方向振动的光，其振动方向与透振方向垂直，所以看不到透射光；沿与竖直方向成45°角振动的光，其振动方向与透振方向不垂直，仍可看到透射光，A、B、D正确．‎ ‎3．登山运动员在登雪山时要注意防止紫外线的过度照射，尤其是眼睛更不能长时间被紫外线照射，否则将会严重地损伤视力．有人想利用薄膜干涉的原理设计一种能大大减小紫外线对眼睛伤害的眼镜．他选用的薄膜材料的折射率为n＝1.5，所要消除的紫外线的频率为ν＝8.1×1014 Hz.‎ ‎(1)他设计的这种“增反膜”所依据的原理是__________．‎ ‎(2)这种“增反膜”的厚度至少是多少？‎ ‎(3)(多选)以下有关薄膜干涉的说法正确的是(　　)‎ A．薄膜干涉说明光具有波动性 B．如果薄膜的厚度不同，产生的干涉条纹一定不平行 C．干涉条纹一定是彩色的 D．利用薄膜干涉也可以“增透”‎ 解析：(1)为了减少进入眼睛的紫外线，应使入射光分别从该膜的前后两个表面反射后形成的反射光叠加后加强，从而使透射的紫外线减弱．‎ ‎(2)路程差(大小等于薄膜厚度d的2倍)应等于光在薄膜中的波长λ′‎ 的整数倍，即2d＝Nλ′(N＝1,2，…)，因此，膜的厚度至少是紫外线在膜中波长的，紫外线在真空中的波长是λ＝≈3.7×10－‎7 m．在膜中的波长是λ′＝≈2.47×10－‎7 m，故膜的厚度至少是1.23×10－‎7 m.‎ ‎(3)干涉和衍射都证明光具有波动性；如果薄膜厚度均匀变化，则干涉条纹一定平行；白光的干涉为彩色条纹，单色光的干涉则为该色光颜色；当膜的厚度为四分之一波长时，两反射光叠加后减弱则会“增透”．故选项A、D正确．‎ 答案：(1)两反射光叠加后加强　(2)1.23×10－7 m ‎(3)AD 区分光的干涉和衍射及双缝干涉时明、暗条纹的判断 ‎(1)白光发生光的干涉、衍射和光的色散都可出现彩色条纹，但其光学本质不同．‎ ‎(2)区分干涉和衍射，关键是理解其本质，实际应用中可以从条纹宽度、条纹间距、亮度等方面加以区分．‎ ‎(3)根据明条纹的判断式Δx＝kλ(k＝0,1,2，…)或暗条纹的判断式Δx＝(2k＋1)(k＝0,1,2，…)，判断出k的取值，从而判断条纹数．‎ 考点二　电磁场和电磁波 ‎1．电磁波的传播及波长、频率、波速 ‎(1)电磁波的传播不需要介质，可在真空中传播，在真空中不同频率的电磁波传播速度是相同的(都等于光速)．‎ ‎(2)不同频率的电磁波，在同一介质中传播，其速度是不同的，频率越高，波速越小．‎ ‎(3)三者关系v＝λf，f是电磁波的频率，即为发射电磁波的LC振荡电路的频率f＝，改变L或C即可改变f，从而改变电磁波的波长λ.‎ ‎2．电磁波与机械波的比较 名称 电磁波 机械波 项目　‎ 研究对象 电磁现象 力学现象 产生 由周期性变化的电场、磁场产生 由质点(波源)的振动产生 波的特点 横波 纵波或横波 波速 在真空中等于光速(很大)(c＝3×108 m/s)‎ 在空气中不大(如声波波速一般为340 m/s)‎ 介质需要 不需要介质(在真空中仍可传播)‎ 必须有介质(真空中不能传播)‎ 能量传播 电磁能 机械能 ‎1．(2016·高考全国甲卷)(多选)关于电磁波，下列说法正确的是(　　)‎ A．电磁波在真空中的传播速度与电磁波的频率无关 B．周期性变化的电场和磁场可以相互激发，形成电磁波 C．电磁波在真空中自由传播时，其传播方向与电场强度、磁感应强度均垂直 D．利用电磁波传递信号可以实现无线通信，但电磁波不能通过电缆、光缆传输 E．电磁波可以由电磁振荡产生，若波源的电磁振荡停止，空间的电磁波随即消失 解析：选ABC.电磁波在真空中的传播速度等于光速，与电磁波的频率无关，选项A正确；周期性变化的电场和磁场可以相互激发，形成电磁波，选项B正确；电磁波传播方向与电场强度、磁感应强度均垂直，选项C正确；电磁波可以通过光缆传输，选项D错误；电磁波波源的电磁振荡停止，波源不再产生新的电磁波，但空间中已产生的电磁波仍可继续传播，选项E错误．‎ ‎2．(2016·福建晋江联考)‎ 声波和电磁波均可传递信息，且都具有波的特征．下列说法正确的是(　　)‎ A．在空气中，电磁波的传播速度大于声波的传播速度 B．声波和电磁波都能引起鼓膜振动 C．电磁波都不能被人看见，声波都能被人听见 D．二胡、电子琴发出的都是电磁波 解析：选A.空气中电磁波的传播速度约为3×108 m/s，而声波在空气中的传播速度为340 m/s，故电磁波的传播速度大于声波的传播速度，选项A正确；声波能引起鼓膜振动，而电磁波不能，选项B错误；电磁波中的可见光可以被人看见，超声波和次声波不能被人听见，选项C错误；二胡、电子琴发出的都是声波，选项D错误．‎ ‎3．我国成功研发的反隐身先进米波雷达堪称隐身飞机的克星，它标志着我国雷达研究又创新的里程碑．米波雷达发射无线电波的波长在1～‎10 m范围内，则对该无线电波的判断正确的是(　　)‎ A．米波的频率比厘米波频率高 B．和机械波一样须靠介质传播 C．同光波一样会发生反射现象 D．不可能产生干涉和衍射现象 解析：选C.无线电波与光波均为电磁波，均能发生反射、干涉、衍射现象，故C正确、D错．电磁波在真空中传播速度最快，故B错．由c＝λf可知，频率与波长成反比，故A错．‎ 对电磁波谱的四点说明 ‎(1)波长不同的电磁波，表现出不同的特性．其中波长较长的无线电波和红外线等，易发生干涉、衍射现象；波长较短的紫外线、X射线、γ射线等，穿透能力较强．‎ ‎(2)电磁波谱中，相邻两波段的电磁波的波长并没有很明显的界线，如紫外线和X射线、X射线和γ射线都有重叠．‎ ‎(3)不同的电磁波，产生的机理不同，无线电波是振荡电路中自由电子的周期性运动产生的；红外线、可见光、紫外线是原子的外层电子受到激发后产生的；X射线是原子的内层电子受到激发后产生的；γ射线是原子核受到激发后产生的．‎ ‎(4)电磁波的能量随频率的增大而增大．‎ 考点三　相对论的理解及简单应用 ‎1．时间间隔的相对性 ‎(1)公式Δt＝.‎ ‎(2)解决时间间隔的相对性应注意 ‎①“动钟变慢”是两个不同惯性系进行时间比较的一种效应，不要认为是时钟的结构或精度因运动而发生了变化；‎ ‎②运动时钟变慢完全是相对的，在它们上面的观察者都将发现对方的钟变慢了．‎ ‎2．长度的相对性 ‎(1)公式l＝l0.‎ ‎(2)解决长度的相对性问题，应当注意：‎ ‎①“动尺缩短”是沿运动方向上的长度比其相对静止时测量的长度要短一些，这种长度收缩并非幻觉，并非看上去短了，它的确变短了，它与物体的具体组成和结构无关，物体运动的速度越接近光速，这种收缩效应就变得越显著；‎ ‎②在具体计算中要明确，长度收缩指的是只在物体运动方向上的长度收缩，在垂直于运动方向上的长度没有变化．‎ ‎3．相对论的三个结论 ‎(1)相对论的速度变换公式u＝.‎ ‎(2)相对论质量m＝.‎ ‎(3)质能方程E＝mc2.‎ ‎1．(2016·河南许昌、新乡、平顶山第二次调研)(多选)1905年，爱因斯坦提出了著名的狭义相对论，给物理学界带来了巨大的进步．根据狭义相对论的理论，下列说法中正确的是(　　)‎ A．在不同的惯性参考系中，一切物理规律都是相同的 B．真空中的光速在不同的惯性参考系中都是相同的 C．根据狭义相对论可知，同时是绝对的 D．根据狭义相对论可知，物体的长度、时间间隔和物体的质量都是相对的 E．根据狭义相对论可知，在相对地面的以速度v高速运动的火车上，当人以相对火车速度u′沿火车前进的方向运动时，则该人相对地面的速度为u＝u′＋v 解析：选ABD.根据狭义相对论可知，在不同的惯性系中，同时是相对的，C错误．E选项中，人相对地面的速度u＝，E错误．‎ ‎2．如图所示，两艘飞船A、B沿同一直线同向飞行，相对地面的速度均为v(v接近光速c)．地面上测得它们的相距为L，则A测得两飞船间的距离________(选填“大于”、“等于”或“小于”)L.当B向A发出一光信号，A测得该信号的速度为________．‎ 解析：从飞船A测量时飞船B是静止时，从地面上测量时两飞船都是运动的，由相对论的“尺缩效应”知运动长度要缩短，故从地面测得的飞船间距小．由光速不变原理知光信号的传播速度与参考系是无关的，故A测得该信号的速度仍为光速c.‎ 答案：大于　c(或光速)‎ ‎3．(2017·湖南长沙模拟)(1)某火箭在地面上的长度为L0，发射后它在地面附近高速(约‎0.3c ‎)飞过，关于地面上的人和火箭中的人观察到的现象，以下说法正确的是(　　)‎ A．下方地面上的人观察到火箭上的时间进程变快了 B．下方地面上的人观察到火箭变短了 C．火箭上的人观察到火箭变短了 D．火箭上的人看到下方地面上的所有物体都变短了 ‎(2)在一飞船上测得飞船的长度为‎100 m，高度为‎10 m．当飞船以‎0.60 c的速度从你身边经过时，按你的测量，飞船有多高、多长？‎ 解析：(1)由时间间隔的相对性知，下方地面上的人观察到火箭上的时间进程变慢了，A错；由长度的相对性知，下方地面上的人观察到火箭变短了，火箭上的人观察到火箭长 度没变，B对、C错；火箭上的人看到在垂直运动方向上，物体的长度不变，D错．‎ ‎(2)因为长度收缩只发生在运动方向上，与运动垂直的方向上没有这种效应，故测得的飞船的高度仍为原来的高度‎10 m．设飞船原长为l0，观测到飞船的长度为l，则根据尺缩效应有l＝l0 ＝100× m＝‎80 m.‎ 答案：(1)B　(2)10 m　80 m 考点四　实验：用双缝干涉测光的波长 ‎1．实验原理：相邻两条明条纹间距Δx与入射光波长λ，双缝S1、S2间距d及双缝与屏的距离l满足的关系式为Δx＝λ.‎ ‎2．实验器材：双缝干涉仪、光具座、光源、学生电源、导线、滤光片、单缝、双缝、遮光筒、毛玻璃屏、测量头、刻度尺．‎ ‎3．实验步骤：‎ ‎(1)安装仪器．‎ ‎①将光源、遮光筒、毛玻璃屏依次安放在光具座上．‎ ‎②接好光源，打开开关，使白炽灯正常发光．调节各部件的高度，使光源灯丝发出的光能沿轴线到达光屏．‎ ‎③安装单缝和双缝，中心位于遮光筒的轴线上，使双缝和单缝的缝平行．‎ ‎(2)观察与记录．‎ ‎①调单缝与双缝间距为5～10 cm时，观察白光的干涉条纹．‎ ‎②在单缝和光源间放上滤光片，观察单色光的干涉条纹．‎ ‎③调节测量头，使分划板中心刻度线对齐第1条亮条纹的中心，记下手轮上的读数a1；转动手轮，使分划板向一侧移动，当分划板中心刻度线与第n条相邻的明条纹中心对齐时，记下手轮上的刻度数a2，则相邻两条纹间的距离Δx＝.‎ ‎④换用不同的滤光片，测量其他色光的波长．‎ ‎(3)数据处理：用刻度尺测量出双缝到光屏间的距离l，由公式λ＝Δx计算波长，重复测量、计算，求出波长的平均值．‎ ‎4．注意事项：‎ ‎(1)调节双缝干涉仪时，要注意调节光源的高度，使它发出的一束光能够沿着遮光筒的轴线把屏照亮．‎ ‎(2)放置单缝和双缝时，缝要相互平行，中心大致位于遮光筒的轴线上．‎ ‎(3)调节测量头时，应使分划板中心刻线和条纹的中心对齐，记清此时手轮上的读数，转动测量头，使分划板中心刻线和另一条纹的中心对齐，记下此时手轮上的读数，两次读数之差就表示这两个条纹间的距离．‎ ‎(4)不要直接测Δx，要测几个条纹的间距，计算得Δx，这样可以减小误差．‎ ‎(5)白光的干涉观察到的是彩色条纹．其中白色在中央，红色在最外边．‎ ‎1．(2017·四川绵阳模拟)用双缝干涉测光的波长，实验中采用双缝干涉仪，它包括以下元件：‎ A．白炽灯 B．单缝片　‎ C．光屏 D．双缝　‎ E．遮光筒　F．滤光片(其中双缝和光屏连在遮光筒上)‎ ‎(1)把以上元件安装在光具座上时，正确的排列顺序是：________.‎ ‎(2)正确调节后，在屏上观察到红光的干涉条纹，用测量头测出10条红亮纹间的距离为a，改用绿色滤光片，其他条件不变，用测量头测出10条绿亮纹间的距离为b，则一定有a________b(填“大于”、“小于”或“等于”)‎ ‎(3)在双缝干涉实验中，滤光片的作用是________，单缝的作用是________，双缝的作用是________．‎ 解析：由于红光的波长大于绿光，根据双缝干涉条纹间隔与波长成正比可知，一定有a大于b.‎ 在双缝干涉实验中，滤光片的作用是获得单色光，单缝的作用是形成线光源，双缝的作用是形成相干光源．‎ 答案：(1)AFBDEC　(2)大于　(3)获得单色光　形成线光源　形成相干光源 ‎2．(2017·甘肃天水模拟)在“用双缝干涉测光的波长”实验中，将测量头的分划板中心刻线与某亮纹中心对齐，将该亮纹定为第1条亮纹，此时手轮上的示数如图甲所示．然后同方向转动测量头，使分划板中心刻线与第6条亮纹中心对齐，记下此时图乙中手轮上的示数为________mm，求得相邻亮纹的间距Δx＝________mm；已知双缝间距d＝2.0×10－‎4 m，测得双缝到屏的距离l＝‎0.700 m，由计算公式λ＝________，求得所测红光的波长为________mm.‎ 解析：题图甲中螺旋测微器的固定刻度读数为2 mm，可动刻度读数为0.01×32.0 mm＝0.320 mm，所以最终读数为2.320 mm，图乙中螺旋测微器的固定刻度读数为13.5 mm，可动刻度读数为0.01×37.0 mm＝0.370 mm，所以最终读数为13.870 mm，故Δx＝mm＝2.310 mm.由Δx＝λ可得λ＝Δx，解得λ＝×2.310 mm＝6.6×10－4mm.‎ 答案：13.870　2.310　Δx　6.6×10－4‎ 课时规范训练 ‎[基础巩固题组]‎ ‎1．(多选)下列有关光学现象的说法中正确的是(　　)‎ A．用光导纤维束传送信息是光的衍射的应用 B．太阳光通过三棱镜形成彩色光谱是光的干涉现象 C．在照相机镜头前加装偏振滤光片拍摄日落时的景物，可使景象更清晰 D．经过同一双缝所得干涉条纹，红光条纹宽度大于绿光条纹宽度 E．激光测距是应用了激光平行性好的特点 解析：选CDE.用光导纤维束传送信息是光的全反射的应用，A错误；太阳光通过三棱镜形成彩色光谱是光的色散现象，是光的折射的结果，B错误；在照相机镜头前加装偏振滤光片拍摄日落时的景物，可减弱反射光，从而使景象更清晰，C正确；红光的波长比绿光的波长长，根据双缝干涉条纹间距公式Δx＝λ可知，经过同一双缝所得干涉条纹，红光条纹宽度大于绿光条纹宽度，D正确；激光的平行性好，常用来精确测距，E正确．‎ ‎2．(多选)下列说法正确的是(　　)‎ A．露珠的晶莹透亮现象，是由光的全反射引起的 B．光波从空气进入水中后，更容易发生衍射 C．电磁波具有偏振现象 D．根据狭义相对论，地面上的人看到高速运行的列车比静止时短 E．物体做受迫振动时，其频率和振幅与自身的固有频率均无关 解析：选ACD.露珠的晶莹透亮现象，是由光的全反射引起的，选项A正确；光波从空气进入水中后，频率不变，波速变小，则波长变短，故不容易发生衍射，选项B错误；因电磁波是横波，故也有偏振现象，选项C正确；根据狭义相对论，地面上的人看到高速运行的列车比静止时短，选项D正确；物体做受迫振动时，其频率总等于周期性驱动力的频率，与自身的固有频率无关，但其振幅与自身的固有频率有关，当驱动力的频率等于固有频率时，振幅最大，选项E错误．‎ ‎3．(多选)下列说法中正确的是(　　)‎ A．医院中用于体检的“B超”利用了超声波的反射原理 B．鸣笛汽车驶近路人的过程中，路人听到的声波频率与波源相比减小 C．在宇宙中高速飞行的飞船中的时钟变慢 ‎ D．照相机镜头的偏振滤光片可使水下影像清晰 E．无线网络信号能绕过障碍物传递到接收终端是利用了干涉原理 解析：选ACD.医院中用于体检的“B超”利用了超声波的反射原理，选项A正确．鸣笛汽车驶近路人的过程中，路人听到的声波频率与波源相比增大，选项B错误．在宇宙中高速飞行的飞船中的时钟变慢，选项C正确．照相机镜头的偏振滤光片可使水下影像清晰，选项D正确．无线网络信号能绕过障碍物传递到接收终端是利用了衍射原理，选项E错误．‎ ‎4．(多选)下列说法正确的是(　　)‎ A．用光导纤维传播信号是利用了光的全反射 B．偏振光可以是横波，也可以是纵波 C．光速不变原理指出光在真空中传播速度在不同惯性参考系中都是相同的 D．光学镜头上的增透膜是利用光的干涉现象 E．声源与观察者相对靠近时，观察者所接收的频率等于声源振动的频率 解析：选ACD.用光导纤维传播信号时，是让携带声音信号的光在光导纤维中进行全反射，从而向前传播的，故A正确；偏振光只能是横波，不可能是纵波，故B错误；据狭义相对论的基本假设知，光速不变原理指出光在真空中传播速度在不同惯性参考系中都是相同的，故C正确；光学镜头上的增透膜是利用光的干涉现象，故D正确；根据多普勒效应知：声源与观察者相对靠近时，观察者所接收的频率大于声源振动的频率，故E错误．‎ ‎5．(多选)下列说法正确的是(　　)‎ A．光的偏振现象说明光是一种横波 B．麦克斯韦预言并用实验验证了电磁波的存在 C．在光的双缝干涉实验中，若仅将入射光由绿色光变为红光，则条纹间距变宽 D．波在介质中传播的频率由波源决定，与介质无关 E．机械波和电磁波都可以在真空中传播 解析：‎ 选ACD.光的偏振现象说明光是一种横波，选项A正确；麦克斯韦预言了电磁波，赫兹用实验验证了电磁波的存在，选项B错误；在光的双缝干涉实验中，若仅将入射光由绿色光变为红光，因红光的波长大于绿光的波长，则根据Δx＝λ可知条纹间距变宽，选项C正确；波在介质中传播的频率由波源决定，与介质无关，选项D正确；机械波传播时需要介质，故不能在真空中传播，E错误．‎ ‎6．(多选)下列说法正确的是(　　)‎ A．在干涉现象中，振动加强点的位移总比减弱点的位移要大 B．单摆在周期性外力作用下做受迫振动，其振动周期与单摆的摆长无关 C．火车鸣笛向我们驶来时，我们听到的笛声频率将比声源发声的频率高 D．当水波通过障碍物时，若障碍的尺寸与波长差不多，或比波长大的多时，将发生明显的衍射现象 E．用两束单色光A、B，分别在同一套装置上做干涉实验，若A光的条纹间距比B光的大，则说明A光波长大于B光波长 解析：选BCE.在波的干涉现象中，所说的振动加强点和振动减弱点，只是从振动幅度的角度来定义的，加强点的振动幅度大，减弱点振动幅度小，但是加强点的位移不一定比减弱点的位移大，A错误；做受迫振动的周期取决于驱动力的周期，与单摆摆长无关，B正确；根据多普勒效应，声源向我们驶来时，我们在单位之间内接受波长的个数增大，即我们听到的笛声频率将比声源发声的频率高，C正确；当孔或障碍物的尺寸与波长差不多或比波长小时，会发生明显的衍射现象，而衍射没有条件，D错误；根据公式Δx＝λ，同一个干涉装置，l和d都是相同的，所以间距越大，波长越大，E正确．‎ ‎7．(多选)下列说法正确的是(　　)‎ A．狭义相对论只涉及无加速运动的惯性系 B．做简谐运动的质点，其振动能量与振幅无关 C．孔的尺寸比波长小才发生衍射现象 D．振荡的电场一定产生同频率振荡的磁场 E．泊松亮斑是光的衍射现象，玻璃中的气泡看起来特别明亮是光的全反射 解析：‎ 选ADE.狭义相对论只涉及无加速运动的惯性系，广义相对论才涉及加速运动的非惯性系，故A正确；做简谐运动的质点，其振动能量与振幅有关，振幅越大，能量越大，故B错误；波发生明显的衍射现象的条件是：当孔、缝的宽度或障碍物的尺寸与波长相比差不多或比波长更小，所以C错误；根据麦克斯韦的电磁理论，振荡的电场一定产生同频率振荡的磁场，故D正确；泊松亮斑是光的衍射现象，玻璃中的气泡看起来特别明亮是光的全反射现象．故E正确．‎ ‎[综合应用题组]‎ ‎8．(多选)如图所示为半圆形的玻璃砖，C为AB的中点，OO′为过C点的AB面的垂线．a、b两束不同频率的单色可见细光束垂直AB边从空气射入玻璃砖，且两束光在AB面上入射点到C点的距离相等，两束光折射后相交于图中的P点，以下判断正确的是(　　)‎ A．在半圆形的玻璃砖中，a光的传播速度大于b光的传播速度 B．a光的频率大于b光的频率 C．两种色光分别通过同一双缝干涉装置形成的干涉条纹，相邻明条纹的间距a光的较大 D．若a、b两束光从同一介质射入真空过程中，a光发生全反射的临界角大于b光发生全反射的临界角 E．b光比a光更容易发生衍射现象 解析：选ACD.由折射光路可知，b光的折射率大于a光，则根据n＝可知，在半圆形的玻璃砖中，a光的传播速度大于b光的传播速度，选项A正确；a光的频率小于b光的频率，选项B错误；因a光的波长大于b光，故a光比b光更容易发生衍射现象，选项E错误；则根据Δx＝λ，则两种色光分别通过同一双缝干涉装置形成的干涉条纹，相邻明条纹的间距a 光的较大，选项C正确；根据sin C＝可知，若a、b两束光从同一介质射入真空过程中，a光发生全反射的临界角大于b光发生全反射的临界角，选项D正确． ‎ ‎9．(1)杨氏干涉实验证明光的确是一种波，一束单色光投射在两条相距很近的狭缝上，两狭缝就成了两个光源，它们发出的光波满足干涉的必要条件，则两列光的________相同．如图所示，在这两列光波相遇的区域中，实线表示波峰，虚线表示波谷，如果放置光屏，在________(选填“A”、“B”或“C”)点会出现暗条纹．‎ ‎(2)在上述杨氏干涉实验中，若单色光的波长λ＝5.89×10－‎7 m，双缝间的距离d＝‎1 mm，双缝到屏的距离l＝‎2 m．求第1个亮条纹到第11个亮条纹的中心间距．‎ 解析：(1)根据发生干涉现象的条件，两列光的频率相同．如果放置光屏，在A，B点会出现亮条纹，在C点会出现暗条纹．‎ ‎(2)相邻亮条纹的中心间距Δx＝λ，‎ 由题意知，亮条纹的数目n＝10，则得L＝nΔx＝ 代入数据解得L＝1.178×10－2 m 答案：(1)频率　C　(2)1.178×10－2 m ‎10．在“用双缝干涉测光的波长”实验中(实验装置如图甲)：‎ ‎(1)下列说法哪一个是错误的(　　)‎ A．调节光源高度使光束沿遮光筒轴线照在屏中心时，应放上单缝和双缝 B．测量某条干涉亮纹位置时，应使测微目镜分划板中心刻线与该亮纹的中心对齐 C．为了减少测量误差，可用测微目镜测出n条亮纹间的距离a，求出相邻两条亮纹间距Δx＝ ‎(2)测量某亮纹位置时，手轮上的示数如图乙所示，其示数为________ mm.‎ 解析：(1)摆放各光具时应保证光线沿直线通过各光具的中心(轴线)，所以摆放时并不放单缝和双缝，A错误．测量亮纹位置时，为了准确，应该将目镜分划板的中心刻线与亮纹中心对齐，B正确．相邻两条亮纹间距为Δx，则n条亮纹间距为a＝(n－1)Δx，即Δx＝，C正确．‎ ‎(2)‎1.5 mm＋47.0×‎0.01 mm＝‎1.970 mm.‎ 答案：(1)A　(2)1.970‎ ‎11．(1)下列说法中不符合事实的是(　　)‎ A．机场安检时，借助X射线能看到箱内物品 B．交通警示灯选用红灯是因为红光更容易穿透云雾烟尘 C．建筑外装涂膜玻璃应用了光的全反射 D．液晶显示应用了偏振光 ‎(2)如图所示，一束激光频率为ν0，传播方向正对卫星飞行方向，已知真空中光速为c，卫星速度为u，则卫星上观测到激光的传播速度为________，卫星接收到激光的频率ν________(填“大于”“等于”或“小于”)ν0.‎ 解析：(1)机场安检时，借助X射线的穿透能力可以看到箱内物品，A正确．交通警示灯选用红灯是因为红光更容易穿透云雾烟尘，B正确．建筑外装玻璃镀一层膜是应用了光的漫反射，C错误．液晶显示应用了偏振光，D正确．‎ ‎(2)由光速不变原理可知，卫星上观测到激光的传播速度是c.由多普勒效应可知，卫星与激光靠近时，卫星接收到激光的频率ν大于ν0.‎ 答案：(1)C　(2)c　大于 ‎12．(1)关于电磁波，下列说法正确的是(　　)‎ A．雷达是用X光来测定物体位置的设备 B．电磁波是横波 C．电磁波必须在介质中传播 D．使电磁波随各种信号而改变的技术叫做解调 ‎(2)某雷达工作时，发射电磁波的波长λ＝‎20 cm，每秒脉冲数n＝5 000，每个脉冲持续时间t＝0.02 μs.‎ ‎①该电磁波的频率为多少？‎ ‎②该雷达的最大侦察距离是多少？‎ 解析：(1)由雷达的工作原理知，雷达是用微波来测定物体位置的设备，A错；电磁波在传播过程中电场强度和磁感应强度总是相互垂直，且与波的传播方向垂直，故电磁 波是横波，B对；电磁波可以不依赖介质而传播，C错；使电磁波随各种信号而改变的技术叫做调制，D错．‎ ‎(2)①根据c＝λf可得 f＝＝ Hz＝1.5×109 Hz.‎ ‎②电磁波在雷达发射相邻两个脉冲间隔时间内传播的距离 s＝cΔt＝c＝3×108× m≈6×‎104 m，‎ 所以雷达的最大侦察距离s′＝＝3×104 m＝30 km.‎ ‎ 答案：(1)B　(2)①1.5×109 Hz　②‎‎30 km 章末检测十四 机械振动　机械波　光　电磁波与相对论(选修3－4)‎ ‎(时间：45分钟　满分：90分)‎ ‎1．(1)(5分)(多选)关于光现象及其应用，下列说法正确的有(　　)‎ A．全息照片用激光来拍摄，主要是利用了激光与物光的相干性高的特点 B．通过手指间的缝隙观察日光灯，可以看到彩色条纹，这是光的偏振现象 C．拍摄玻璃橱窗内的物品时，在镜头前加一个偏振片可以减小玻璃表面反射光的强度 D．当观察者向静止的声源运动时，观察者接收到的声波频率低于声源的频率 E．一束单色光由空气射入玻璃，这束光的速度变慢，波长变短 ‎(2)(10分)已知某机械横波在某时刻的波形图如图所示，波沿x轴正方向传播，质点P与坐标原点O的水平距离为‎0.32 m，从此时刻 计时．‎ ‎①若波速大小为2 m/s，则至少间隔多长时间重复出现波形图？‎ ‎②若质点P经0.8 s第一次达到正向最大位移，求波速大小．‎ ‎③若质点P经0.4 s到达平衡位置，求波速大小．‎ 解析：(1)全息照片用激光来拍摄，利用了激光与物光的相干性高的特点，A正确；通过手指间的缝隙观察日光灯，可看到彩色条纹，这是光的衍射现象，B错误；照相机镜头前加偏振片可以减小玻璃表面反射光的强度，从而使玻璃后的影像清晰，C正确；当观察者向静止的声源运动时，接收到的声波的频率将高于声源的频率，故D错误；光从空气射入玻璃中，其频率f不变，又由n＝得速度v变小，再由v＝λf得λ变小，故E正确．‎ ‎(2)①由图可知，波长λ＝‎0.8 m，根据题意，T＝代入数据解得周期T＝0.4 s ‎②波沿x轴正方向传播，质点P第一次达到正向最大位移时，波传播了Δx＝0.32 m－0.2 m＝0.12 m 波速v＝＝0.15 m/s ‎③波沿x轴正方向传播，质点P第一次到达平衡位置时，波传播了Δx＝0.32 m，由周期性可知波0.4 s内传播的可能距离 xn＝(0.32＋n)m(n＝0,1,2，…)‎ 波速v＝(0.8＋n)m/s(n＝0,1,2，…)‎ 答案：(1)ACE　(2)①0.4 s　②0.15 m/s ‎③v＝(0.8＋n)m/s(n＝0,1,2，…)‎ ‎2．(1)(5分)(多选)‎2015年12月30日在新疆阿克陶县发生3.3级地震，震源深度‎7 km.如果该地震中的简谐横波在地球中匀速传播的速度大小为 ‎‎4 km ‎/s，如图所示，波沿x轴正方向传播，某时刻刚好传到N处，则(　　)‎ A．从波源 振动到波源迁移到地面需要1.75 s时间 B．波的周期为0.015 s C．从波传到N处 计时，经过t＝0.03 s位于x＝‎240 m处的质点加速度最小 D．图示时刻，波的图象上M点的速度沿y轴负方向，经过一段极短时间动能减小 E．图示时刻，波的图象上除M点外与M点势能相等的质点有7个 ‎(2)(10分)某探究小组的同学利用直角三棱镜做光学实验，直角三棱镜的截面如图所示，棱镜的折射率为，α＝30°，BC边长度为a.P为垂直于直线BCO的光屏．现有一宽度等于AB边长度的平行单色光束垂直射向AB面，已知sin 75°＝＋，cos 75°＝－.求：‎ ‎①光线从AC面射出时的折射角；‎ ‎②在光屏P上被折射光线照亮的光带的宽度．‎ 解析：(1)波上质点并不随波迁移，选项A错误；由题意可知该波的周期为T＝＝0.015 s，从波传到x＝120 m处 计时，经过t＝0.03 s，波刚好传到x＝240 m处，位于x＝240 m处的质点在平衡位置，加速度最小，选项B、C正确；由“上下坡”法可得，题图所示时刻，M点的速度沿y轴负方向，正在向平衡位置运动，速度增大，则动能增大，选项D错误；由简谐运动的对称性可得除M点外与M点势能相等的质点有7个，选项E正确．‎ ‎(2)①光线在AB面上折射后方向不变，射到AC面上的入射角i＝30°‎ 如图甲所示，折射角为r，根据折射定律有sin 30°＝sin r得r＝45°‎ ‎②如图乙所示，可画出折射光线在光屏上的光带宽度等于CE ‎∠EAC＝45°，∠ECA＝30°，AC＝2a 在△AEC中，根据正弦定理有 ＝ 解得CE＝(2－2)a 答案：(1)BCE　(2)①45°　②(2－2)a ‎3．(1)(5分)如图甲所示，在光滑的斜面上有一滑块，一劲度系数为k的轻弹簧上端与滑块相邻，下端与斜面上的固定挡板连接，在弹簧与挡板间有一力传感器(压力显示为正值，拉力显示为负值)，能将各时刻弹簧中的弹力数据实时传送到计算机，经计算机处理后在屏幕上显示出F－t图象，现用力将滑块沿斜面压下一段距离，放手后滑块将在光滑斜面上做简谐运动，此时计算机屏幕上显示出如图乙所示的图象．‎ ‎①滑块做简谐运动的回复力是由________________提供的；‎ ‎②由图乙所示的F－t图象可知，滑块做简谐运动的周期为________ s；‎ ‎③结合F－t图象的数据和题目中已知条件可知，滑块做简谐运动的振幅为________．‎ ‎(2)(10分)一赛艇停在平静的水面上，赛艇前端有一标记P离水面的高度为h1＝‎0.6 m，尾部下端Q略高于水面，赛艇正前方离赛艇前端s1＝‎0.8 m处有一浮标，如图所示，一潜水员在浮标前方s2＝‎3.0 m处下潜到深度为h2时，看到标记刚好被浮标挡住，此处看不到船尾端Q；继续下潜Δh＝‎2.0 m，恰好能看见Q、‎ ，求：‎ ‎①深度h2　②赛艇的长度l(可用根式表示)‎ 解析：(1)对滑块进行受力分析，回复力指物块所受力的合力；由F－t图象分析滑块的周期；根据胡克定律求出弹簧的伸长量和压缩量，中间位置为平衡位置，从而可以求出振幅．‎ ‎①对滑块进行受力分析，滑块的合力为：弹簧的弹力和重力沿斜面的分力的合力，合力提供回复力；‎ ‎②由图可以看出周期为0.4 s；‎ ‎③根据胡克定律：‎ F1＝kx，F2＝kx′振幅d＝＝ ‎(2)解决光学问题的关键要掌握全反射的条件、折射定律n＝、临界角公式sin C＝、光速公式v＝，运用几何知识结合解决这类问题．‎ ‎①设过P点光线，恰好被浮标挡住时，入射角、折射角分别为：α、β 则： sin α＝，sin β＝，n＝，由①②③得：h2＝4 m ‎②潜水员和Q点连线与法线之间的夹角刚好为临界角C，则：sin C＝＝ cot C＝ 由④⑤得： l＝ m 答案：(1)①弹簧的弹力和重力沿斜面的分力的合力 ‎②0.4 　③ ‎ ‎(2)①h2＝‎4 m　②l＝ m ‎4．(1)(5分)(多选)如图所示，实线表示两个相干波源S1、S2发出的波的波峰位置，设波的周期为T1，波长为λ，波的传播速度为v，下列说法正确的是________．‎ A．图中的a点为振动减弱点的位置 B．图中的b点为振动加强点的位置 C．波源S1的波经过干涉之后波的性质完全改变 D．v＝λT E．从图中时刻 ，波源S1的波峰传播到a、b位置的最短时间均为 ‎(2)(10分)某同学做“测定玻璃的折射率”实验时，用他测得的多组入射角i与折射角r作出sin i－sin r的图象，如图甲所示．‎ ‎　‎ ‎①求该玻璃的折射率n；‎ ‎②他再取用该种玻璃制成的直角三棱镜，入射光的方向垂直于斜边，如图乙所示；则角θ在什么范围内，入射光经过两次全反射又从斜边射出．‎ 解析：(1)由图可知，a质点是波峰与波谷相遇，为振动减弱点的位置，A正确；b点到两波源的距离相等，是波峰与波峰相遇处、波谷与波谷相遇处，为振动加强点的位置，B正确；波源S1的波经过干涉之后波的性质不变，C错误；v＝，D错误；波在同一均匀介质中是匀速传播的，从图中时刻，波源S1的波峰到a ‎、b平衡位置的距离都是半个波长，所以波源S1的波峰传播到a、b位置的最短时间均为，E正确．‎ ‎(2)①由图甲可计算出该玻璃的折射率为 n＝＝＝2.‎ ‎②光的传播方向如图所示，欲使入射光在上侧直角边发生全反射，须sin θ＞sin C＝＝ 解得：θ ＞30°‎ 又当光线行进至右侧直角边时，入射角为90°－θ，欲使入射光在该边发生全反射，须 ‎ sin(90°－θ)＞sin C＝＝.‎ 解得：θ＜60°‎ 所以θ的范围为：30°＜θ＜60°‎ 答案：(1)ABE　(2)①n＝2　②30°＜θ＜60°‎ ‎5．(1)(5分)(多选)一列简谐横波沿x轴传播．图中(甲)图是t＝0时刻的波形，且x＝‎4.0 m处质点刚好起振．(乙)图是x＝‎4.0 m处质点经t＝1.0 s后的位移时间图象．下列说法中不正确的是(　　)‎ A．该波‎6.0 m处的质点，第一次到达波峰的时间为3.0 s B．该波‎6.0 m处的质点，第一次到达波谷的时间为6.0 s C．该波上的E、F两质点同时达到波峰位置和平衡位置 D．该波沿x轴负方向传播 E．该波x＝‎1.0 m处的质点从图示时刻起历时3.0 s通过‎6.0 cm的路程 ‎(2)(10分)如图所示，在MN的下方足够大的空间是玻璃介质，其折射率n＝，玻璃介质的上边界MN是屏幕．玻璃中有一个正三角形空气泡，其边长l＝‎40 cm，顶点与屏幕接触于C点，底边AB与屏幕平行．一束激光a垂直于AB边射向AC边的中点O，结果在屏幕MN上出现两个光斑. ‎ ‎①求两个光斑之间的距离L.‎ ‎②若任意两束相同的激光同时垂直于AB边向上射入空气泡，求屏幕上相距最远的两个光斑之间的距离．‎ 解析：(1)由图甲可知λ＝4 m，由x＝4.0 m处质点1 s后位于最大位移处可知波的周期T＝0.4 s，v＝＝10 m/s，则波2 s后到达6.0 m处，该质点再经过1 s到达波峰，A正确；6.0 m处的质点从波峰到波谷的时间为2 s，即第一次到达波谷的时间为5 s，B错误；质点从平衡位置到最大位移的过程中速度一直减小，所以质点E回到平衡位置的时间大于F点到最大位移处的时间，C错误； 根据t＝0时刻x＝4.0 m处质点刚好起振，证明波向右传播，D错误；该波x＝1.0 m处的质点从图示时刻起历时3.0 s通过6.0 cm的路程，E正确．‎ ‎(2)①画出光路图如图甲所示．在界面AC，入射角i＝60°，由折射定律＝n解得折射角r＝30°由光的反射定律得反射角θ＝60°‎ 由几何关系得，△ODC是边长为l的正三角形，△OEC为等腰三角形，且CE＝OC＝ 则两个光斑之间的距离 L＝DC＋CE＝‎40 cm. ‎ ‎②作出入射点在A、B的光线的光路图，如图乙所示，由图可得屏幕上相距最远的两个光斑之间的距离PQ＝2l＝80 cm.‎ 答案：(1)BCD　 (2)①40 cm　②80 cm ‎6．(1)(5分)如图所示，含有a、b两种单色光的一细光束，沿半径方向从真空射入横截面为半圆形的透明介质中．a、b两种单色光从介质中射出时方向如图所示．则a、b两种单色光在介质中的折射率n1∶n2＝________，两种单色光在介质中的速度v1∶v2＝________.‎ ‎(2)(10分)一列沿x轴正方向传播的简谐横波在t＝0时刻的波形如图所示，P质点此时的位移为‎10 cm，振幅为‎20 cm.P质点再经过 s第一次到达波峰，求：‎ ‎①P质点的位移y与时间t的函数关系；‎ ‎②该简谐横波的波速．‎ 解析：(1)设入射角为i，根据折射定律得n1＝ n2＝ 则＝＝；‎ 由v＝得两种单色光在介质中的速度v1∶v2＝2∶ ‎(2)①P质点的位移y与时间t的函数关系 y＝20sin(ωt＋φ0)‎ t＝0 s时 y＝‎10 cm得：φ0＝ t＝ s时y＝‎20 cm得： ω＝5π P质点的位移y与时间t的函数关系y＝20sin cm ‎② T＝＝0.4 s 该简谐横波的波速v＝10 m/s.‎ 答案：(1)∶2　2∶　(2)①y＝20sin ‎②v＝10 m/s