2020高中物理第一章抛体运动第2节运动的合成与分解2剖析小船渡河、关联速度学案2 4页

剖析小船渡河、关联速度 一、考点突破：‎ 考点 课程目标 备注 小船渡河 关联速度 1. ‎ 掌握小船渡河的合运动和分运动的关系；‎ ‎2. 掌握关联速度的分解方法 高考对本知识点的考查侧重在对运动的合成与分解方法的考查，常会在动力学、能量守恒的知识中融入本知识点，并作为解题的关键条件进行考查。‎ 二、重难点提示：‎ 重点：1. 掌握小船渡河的合运动和分运动的关系；‎ ‎2. 掌握关联速度的分解方法。‎ 难点：关联速度的分解方法。‎ 一、小船渡河问题分析 ‎（1）船的实际运动是水流的运动和船相对静水的运动的合运动。‎ ‎（2）三种速度：v1（船在静水中的速度）、v2（水流速度）、v（船的实际速度）。‎ ‎（3）三种情景 ‎①过河时间最短：船头正对河岸时，渡河时间最短，t短＝（d为河宽）。‎ ‎②过河路径最短（v2v1时）：合速度不可能垂直于河岸，无法垂直渡河。确定方法如下：如图所示，以v2矢量末端为圆心，以v1矢量的大小为半径画弧，从v2矢量的始端向圆弧作切线，则合速度沿此切线方向航程最短，由图可知：cosα＝，最短航程：s短＝＝d。‎ 二、“关联”速度问题——绳（杆）端速度分解模型 ‎1. 模型特点 4‎ 沿绳（或杆）方向的速度分量大小相等。‎ ‎2. 思路与方法 合运动→绳拉物体的实际运动速度v 方法：v1与v2的合成遵循平行四边形定则。‎ ‎3. 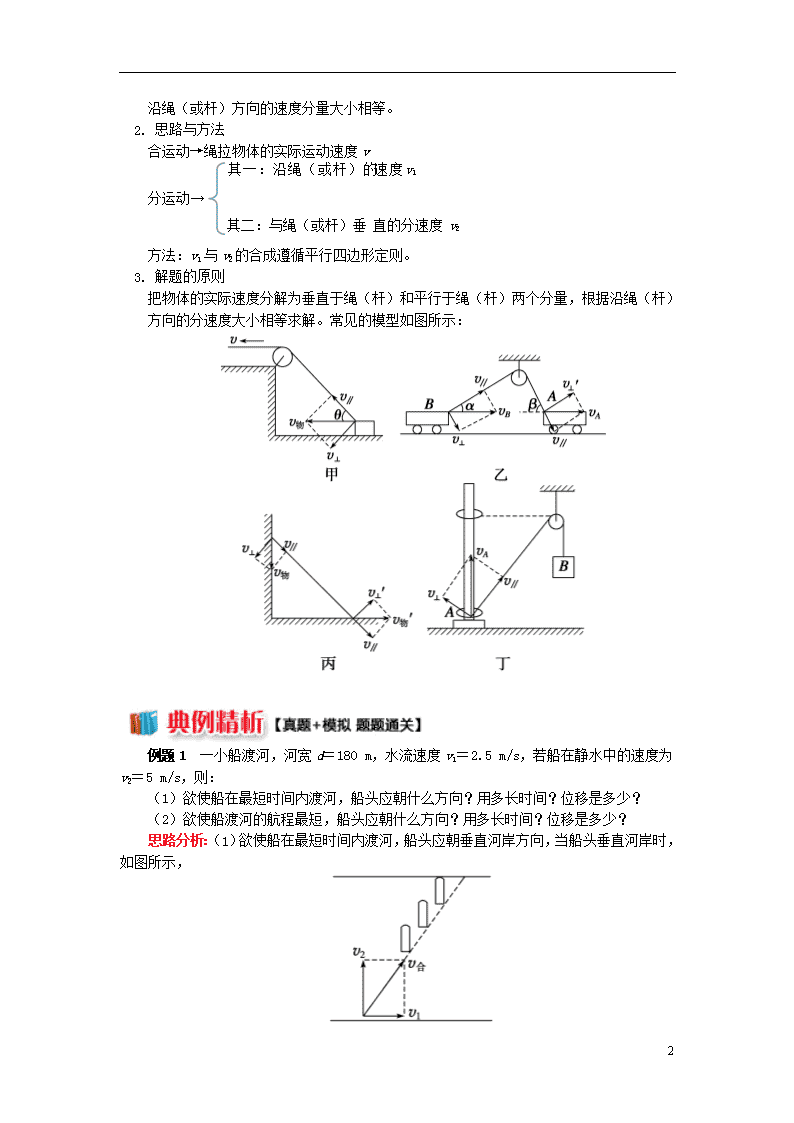解题的原则 把物体的实际速度分解为垂直于绳（杆）和平行于绳（杆）两个分量，根据沿绳（杆）方向的分速度大小相等求解。常见的模型如图所示：‎ ‎ ‎ 例题1 一小船渡河，河宽d＝‎180 m，水流速度v1＝‎2.5 m/s，若船在静水中的速度为v2＝‎5 m/s，则：‎ ‎（1）欲使船在最短时间内渡河，船头应朝什么方向？用多长时间？位移是多少？‎ ‎（2）欲使船渡河的航程最短，船头应朝什么方向？用多长时间？位移是多少？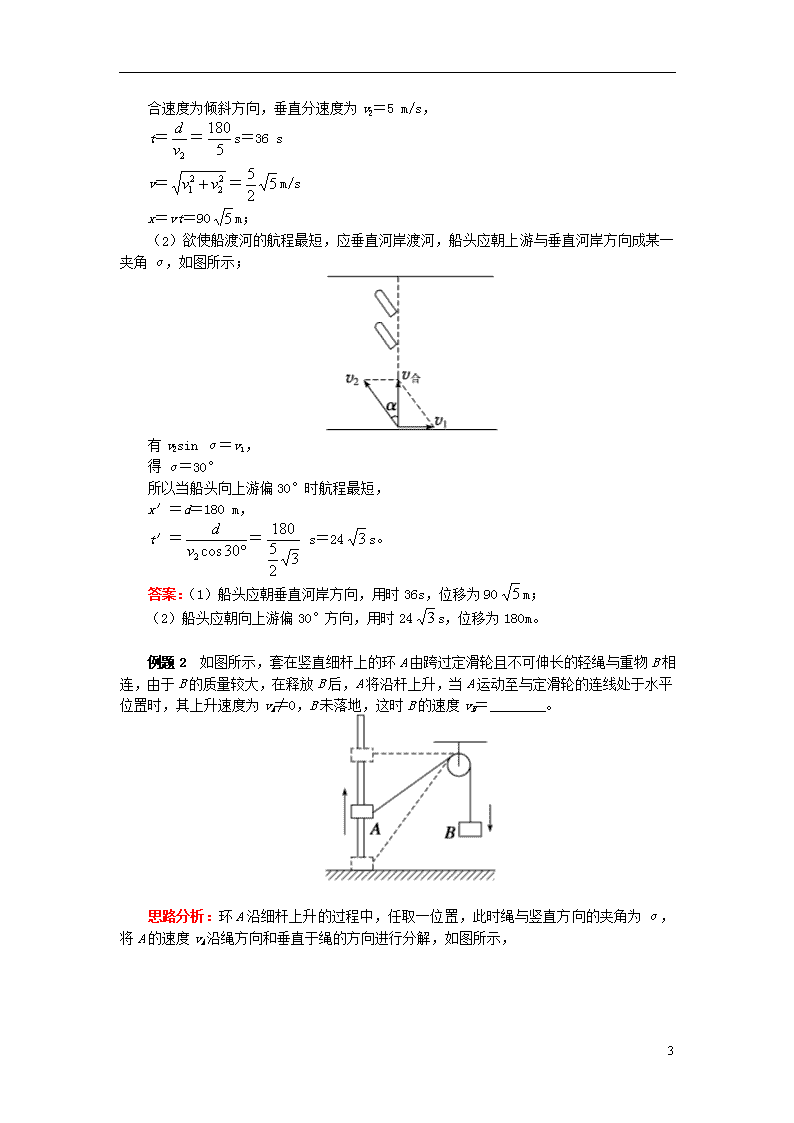‎ 思路分析：（1）欲使船在最短时间内渡河，船头应朝垂直河岸方向，当船头垂直河岸时，如图所示，‎ 4‎ 合速度为倾斜方向，垂直分速度为v2＝‎5 m/s，‎ t＝＝s＝36 s v＝＝m/s x＝vt＝‎90‎m；‎ ‎（2）欲使船渡河的航程最短，应垂直河岸渡河，船头应朝上游与垂直河岸方向成某一夹角α，如图所示；‎ 有v2sin α＝v1，‎ 得α＝30°‎ 所以当船头向上游偏30°时航程最短，‎ x′＝d＝‎180 m，‎ t′＝＝ s＝24s。‎ 答案：（1）船头应朝垂直河岸方向，用时36s，位移为‎90m；‎ ‎（2）船头应朝向上游偏30°方向，用时24s，位移为‎180m。‎ 例题2 如图所示，套在竖直细杆上的环A由跨过定滑轮且不可伸长的轻绳与重物B相连，由于B的质量较大，在释放B后，A将沿杆上升，当A运动至与定滑轮的连线处于水平位置时，其上升速度为vA≠0，B未落地，这时B的速度vB＝________。‎ 思路分析：环A沿细杆上升的过程中，任取一位置，此时绳与竖直方向的夹角为α，将A的速度vA沿绳方向和垂直于绳的方向进行分解，如图所示，‎ 4‎ 则v1＝vAcos α，B下落的速度vB＝v1＝vAcos α，当环A上升至与定滑轮的连线处于水平位置时α＝90°，所以此时B的速度vB＝0。‎ 答案：0‎ ‎【方法提炼】‎ 解决关联问题时应把握以下两点：‎ ‎（1）确定合速度，它应是物体的实际速度；‎ ‎（2）物体的运动引起了两个效果：一是绳子的收缩，二是绳绕滑轮的转动，应根据实际效果进行运动的分解。‎ 满分训练：如图所示，一人站在岸上，利用绳和定滑轮拉船靠岸，在某一时刻绳的速度为v，绳AO段与水平面的夹角为θ，OB段与水平面的夹角为α，不计摩擦和轮的质量，则此时小船的速度多大？‎ 思路分析：小船的运动引起了绳子的收缩以及绳子绕定滑轮转动的效果，所以将小船的运动分解到绳子收缩的方向和垂直于绳子的方向，分解如图所示，则由图可知 vA＝‎ 答案：‎ 4‎