新教材高中物理第3章圆周运动第3节离心现象课件鲁科版必 47页

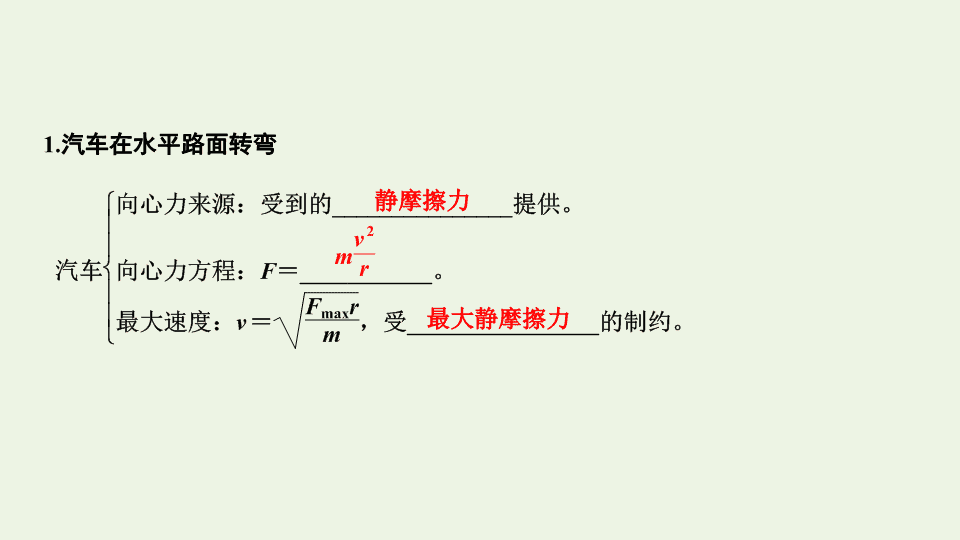
第 3 节　离心现象 核心素养 物理观念 科学探究 科学思维 科学态度与责任 1. 会分析汽车、火车转弯时的向心力来源。 2. 会分析汽车过凸形桥和凹形桥时的向心力来源。 3. 理解轻绳模型和轻杆模型的相同点和不同点。 4. 知道什么是离心运动和离心运动产生的条件。 竖直面内圆周运动的临界条件。 离心运动产生的条件。 通过分析火车转弯问题了解火车转弯的速度与安全的关系。 知识点一　车辆转弯时所需的向心力 [ 观图助学 ] 观察上图，火车转弯处的轨道和自行车赛转弯处的赛道有什么共同特点，为什么要这样设计？ 1. 汽车在水平路面转弯 静摩擦力 最大静摩擦力 2. 汽车、火车在内低外高的路面上转弯 mg tan θ 转弯半径 [ 思考判断 ] (1) 汽车在水平路面上正常转弯时所需要的向心力是滑动摩擦力提供的。 ( ) (2) 铁路的轨道，内、外轨道都是一样高。 ( ) (3) 火车转弯时，如果速度合适，则不会对轨道产生侧向的压力。 ( ) × × √ 知识点二　竖直面内的圆周运动 [ 观图助学 ] 观察上图，过山车在最高点时和汽车过拱桥时，都是什么力提供向心力？ 1. 汽车过拱形桥 分类 分析　　 汽车过凸形桥 汽车过凹形桥 向心力 支持力与重力的合力提供向心力 支持力与重力的合力提供向心力 mg － N N － mg 小于 大于 2. 过山车 ( 在最高点和最低点 ) N ＋ mg N ′ － mg [ 思考判断 ] (1) 汽车过拱形桥时，对桥面的压力一定大于汽车自身的重力。 ( ) (2) 过山车运动到最高点时之所以不掉下来是因为受到了向上的作用力。 ( ) (3) 过山车经过轨道最低点时对轨道的压力大于自身的重力。 ( ) × × √ 知识点三　生活中的离心运动 1. 离心运动 (1) 定义 做圆周运动的物体，在受到合外力突然 或者 提供圆周运动所需要的向心力的情况下，将 运动。 (2) 条件 合外力突然 或合外力 提供向心力。 消失 不足以 远离圆心 消失 不足以 2. 离心运动的应用和防止 (1) 应用 离心分离器、离心干燥器、脱水筒、 。 (2) 危害与防止 危害：如果过荷太大时，飞行员会暂时失明，甚至昏厥。 防止：如车辆转弯时要 。 离心水泵 限速 [ 思考判断 ] (1) 做离心运动的物体沿半径方向远离圆心。 ( ) (2) 做圆周运动的物体只有突然失去向心力时才做离心运动。 ( ) (3) 当半径方向的合外力不足以提供物体做圆周运动所需的向心力时，物体沿圆周与切线之间的曲线做离心运动。 ( ) × × √ 火车转弯问题分析 核心要点 [ 要点归纳 ] 1. 火车车轮的特点 火车的车轮有凸出的轮缘，火车在铁轨上运行时，车轮与铁轨有水平与竖直两个接触面，这种结构特点，主要是避免火车运行时脱轨，如图所示。 其中 R 为弯道半径， θ 为轨道所在平面与水平面的夹角， v 为转弯处的规定速度。 4. 转弯时速度与轨道侧压力的关系 [ 经典示例 ] [ 例 1] 修铁路时，两轨间距是 1 435 mm ，某处铁路转弯的半径是 300 m ，若规定火车通过这里的速度是 72 km/h 。请你运用学过的知识计算一下，要想使内、外轨均不受轮缘的挤压，内、外轨的高度差应是多大？ 解析 　火车受到的支持力和重力的合力指向轨道圆心做向心力，如图所示。 答案 　 0.195 m 方法总结　火车转弯问题的解题方法 (1) 对火车转弯问题一定要搞清合力的方向，指向圆心方向的合外力提供物体做圆周运动的向心力，方向指向水平面内的圆心。 (2) 弯道两轨在同一水平面上时，向心力由外轨对轮缘的挤压力提供。 (3) 当外轨高于内轨时，向心力由火车的重力和铁轨的支持力以及内、外轨对轮缘的挤压力的合力提供，这与火车的速度大小有关。 [ 针对训练 1] 火车在拐弯时，关于向心力的分析，正确的是 ( 　　 ) A. 由于火车本身作用而产生了向心力 B. 主要是由于内、外轨的高度差的作用，车身略有倾斜，车身所受重力的分力产生了向心力 C. 火车在拐弯时的速率小于规定速率时，内轨将给火车侧压力，侧压力就是向心力 D. 火车在拐弯时的速率大于规定速率时，外轨将给火车侧压力，侧压力作为火车拐弯时向心力的一部分 解析 　火车正常拐弯时，重力和支持力的合力提供向心力，故 A 、 B 错误；当拐弯速率大于规定速率时，外轨对火车有侧压力作用；当拐弯速率小于规定速率时，内轨对火车有侧压力作用，此时，火车拐弯所需的向心力是重力、支持力和侧压力的合力来提供，故 C 错误， D 正确。 答案 　 D 竖直平面内圆周运动分析 [ 情境探究 ] 如图所示，一辆汽车以恒定的速度在起伏不平的路面上行进，图中标出的 4 个点中，汽车在哪一点对路面的压力最大？在哪一点对路面的压力最小呢？在哪一点容易发生 “ 飞车 ” 现象？ 核心要点 答案 　在最低点 B 时对路面的压力最大；在最高点 C 时对路面的压力最小，易发生 “ 飞车 ” 现象。 [ 探究归纳 ] 1. 汽车过拱形桥问题 2. 竖直平面内圆周运动的两类模型 (2) 轻杆模型 如图所示，在细轻杆上固定的小球或在管形轨道内运动的小球，由于杆和管能对小球产生向上的支持力，所以小球能在竖直平面内做圆周运动的条件是在最高点的速度大于或等于零。在最高点 [ 经典示例 ] [ 例 2] 杂技演员在做 “ 水流星 ” 表演时，用一根细绳系着盛水的杯子，抡起绳子，让杯子在竖直平面内做圆周运动。如图所示，杯内水的质量 m ＝ 0.5 kg ，绳子总长 l ＝ 120 cm ， g 取 9.8 m/s 2 。求： (1) 在最高点水不流出的最小速率。 (2) 水在最高点速率 v ＝ 3 m/s 时，水对杯底的压力大小。 由牛顿第三定律知，水对杯子的压力大小 N ′ ＝ N ＝ 2.6 N 。 答案 　 (1)2.42 m/s 　 (2)2.6 N 方法总结　竖直平面内圆周运动的分析方法 (1) 明确运动的模型，是轻绳模型还是轻杆模型。 (2) 明确物体的临界状态，即在最高点时物体具有最小速度时的受力特点。 (3) 分析物体在最高点及最低点的受力情况，根据牛顿第二定律列式求解。 解之得 F B ＝ mg ， 解之得 F A ＝ 7 mg ， 所以在 A 、 B 两点轨道对车的压力大小相差 6 mg 。 答案 　 6 mg [ 情境探究 ] 雨天，当你旋转自己的雨伞时，会发现水滴沿着伞的边缘切线飞出。汽车高速转弯时，若摩擦力不足，汽车会滑出路面。请思考： 生活中的离心运动 核心要点 (1) 水滴飞出、汽车滑出是因为受到了离心力吗？ (2) 物体做离心运动的条件是什么？ (3) 汽车转弯发生侧翻会向外翻还是向内翻？ 答案 　 (1) 水滴飞出、汽车滑出的原因是物体惯性的表现，不是因为受到了什么离心力，离心力是不存在的。 (2) 物体做离心运动的条件是做圆周运动的物体，提供向心力的外力突然消失或者外力不能提供足够大的向心力。 (3) 由于外力不足以提供向心力，所以向外翻。 [ 探究归纳 ] 1. 离心运动中合外力与向心力的关系 2. 常见几种离心运动对比图示 项 目 实物图 原理图 现象及结论 洗衣机脱水筒 当水滴跟物体的附着力 F 不足以提供向心力时，即 F ＜ mω 2 r ，水滴做离心运动 3. 离心现象的防止 (1) 汽车在公路转弯处限速：在水平公路上行驶的汽车，转弯时所需要的向心力是由车轮与路面间的静摩擦力提供的。如果转弯时速度过大，所需向心力 F 大于最大静摩擦力 f max ，汽车将做离心运动而造成车体侧滑，因此在公路转弯处汽车必须限速。 (2) 转动的砂轮、飞轮限速：高速转动的砂轮、飞轮等，都不得超过允许的最大转速，如果转速过高，砂轮、飞轮内部分子间的作用力不足以提供所需的向心力，离心运动会使它们破裂，甚至酿成事故。 [ 经典示例 ] [ 例 3] ( 多选 ) 如图是摩托车比赛转弯时的情形，转弯处路面常是外高内低，摩托车转弯有一个最大安全速度，若超过此速度，摩托车将发生滑动。对于摩托车滑动的问题，下列论述正确的是 ( 　　 ) A. 摩托车一直受到沿半径方向向外的离心力作用 B. 摩托车所受外力的合力小于所需的向心力 C. 摩托车将沿其线速度的方向与半径向外的方向之间做离心运动 D. 摩托车将沿其半径方向沿直线滑去 解析 　摩托车只受重力、地面支持力和地面的摩擦力作用，没有离心力， A 项错误；摩托车正常转弯时可看作是做匀速圆周运动，所受的合力等于向心力，如果向外滑动，说明合力小于需要的向心力， B 项正确；摩托车将在沿线速度方向与半径向外的方向之间做离心曲线运动， C 项正确， D 项错误。 答案 　 BC [ 针对训练 3] ( 多选 ) 如图甲所示，在光滑水平转台上放一木块 A ，用细绳的一端系住木块 A ，另一端穿过转台中心的光滑小孔 O 悬挂另一木块 B 。当转台以角速度 ω 匀速转动时， A 恰能随转台一起做匀速圆周运动，图乙为其俯视图，则 ( 　　 ) A. 当转台的角速度变为 1.5 ω 时，木块 A 将沿图乙中的 a 方向运动 B. 当转台的角速度变为 1.5 ω 时，木块 A 将沿图乙中的 b 方向运动 C. 当转台的角速度变为 0.5 ω 时，木块 A 将沿图乙中的 b 方向运动 D. 当转台的角速度变为 0.5 ω 时，木块 A 将沿图乙中的 c 方向运动 解析 　木块 A 以角速度 ω 做匀速圆周运动时的向心力由细绳的拉力提供，大小等于木块 B 所受的重力，而木块 B 所受重力不变，所以转台角速度增大时，木块 A 需要的向心力大于 B 所受的重力，木块 A 做离心运动， a 为绳继时木块 A 的运动方向，选项 B 正确；转台角速度减小时，木块 A 需要的向心力小于木块 B 所受的重力，木块 A 做靠近圆心的运动，选项 D 正确。 答案 　 BD