【物理】2019届一轮复习人教版 万有引力与航天 学案 13页

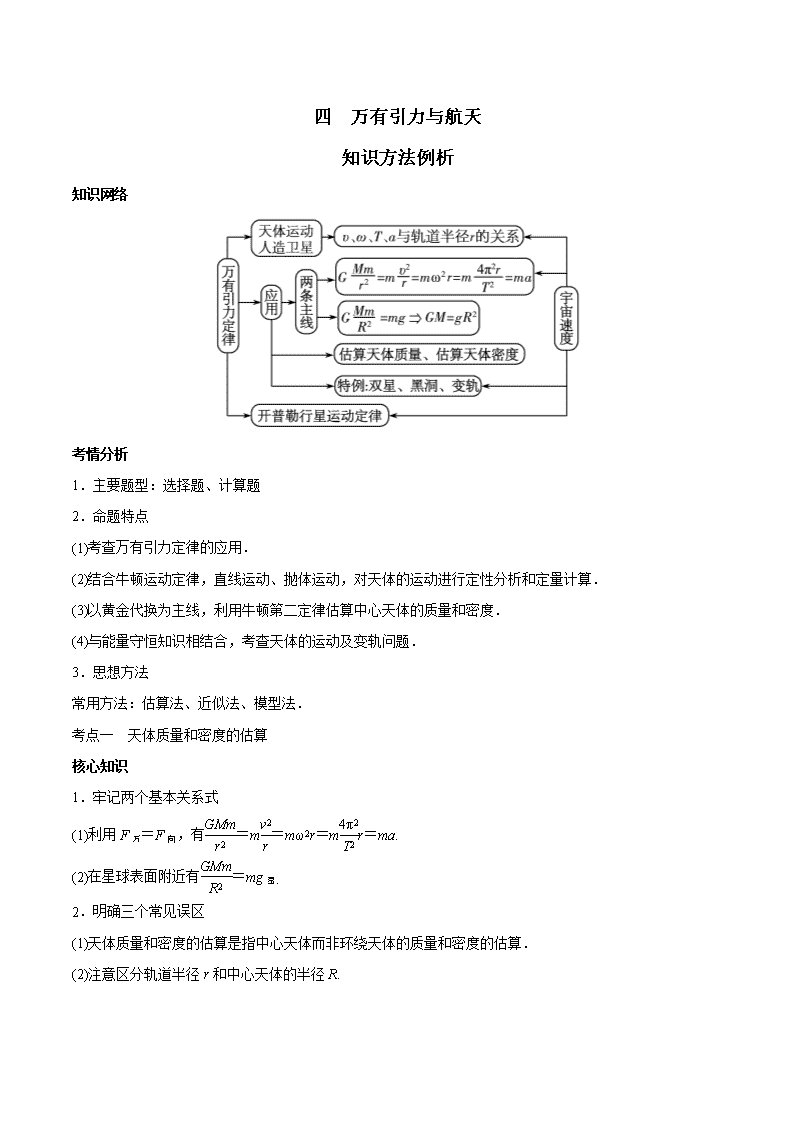
四 万有引力与航天 知识方法例析 知识网络 考情分析 ‎1．主要题型：选择题、计算题 ‎2．命题特点 ‎(1)考查万有引力定律的应用．‎ ‎(2)结合牛顿运动定律，直线运动、抛体运动，对天体的运动进行定性分析和定量计算．‎ ‎(3)以黄金代换为主线，利用牛顿第二定律估算中心天体的质量和密度．‎ ‎(4)与能量守恒知识相结合，考查天体的运动及变轨问题．‎ ‎3．思想方法 常用方法：估算法、近似法、模型法．‎ 考点一　天体质量和密度的估算 核心知识 ‎1．牢记两个基本关系式 ‎(1)利用F万＝F向，有＝m＝mω2r＝mr＝ma.‎ ‎(2)在星球表面附近有＝mg星．‎ ‎2．明确三个常见误区 ‎(1)天体质量和密度的估算是指中心天体而非环绕天体的质量和密度的估算．‎ ‎(2)注意区分轨道半径r和中心天体的半径R.‎ ‎(3)在考虑自转问题时，只有两极才有＝mg.‎ 规律方法 估算中心天体质量和密度的两条思路 ‎(1)利用天体表面的重力加速度和天体半径估算 由G＝mg得M＝，再由ρ＝，V＝πR3得ρ＝.‎ ‎(2)已知天体做匀速圆周运动的轨道半径和周期，由G＝mr得M＝，再结合ρ＝，V＝πR3得ρ＝ρ＝.‎ 典例分析 ‎【例1】　假设地球可视为重量均匀分布的球体．已知地球表面重力加速度在两极的大小为g0，在赤道的大小为g；地球自转的周期为T，引力常量为G.地球的密度为(　　)‎ A. B. C. D. ‎【答案】　B ‎【例2】　宇宙中有两颗相距无限远的恒星s1、s2，半径均为R0.图分别是两颗恒星周围行星的公转周期T2与公转半径r3的图象，则(　　)‎ A．恒星s1的质量大于恒星s2的质量 B．恒星s1的密度小于恒星s2的密度 C．恒星s1的第一宇宙速度大于恒星s2的第一宇宙速度 D．距两恒星表面高度相同的行星，s1的行星向心加速度较大 ‎【答案】　B ‎【解析】　行星绕恒星做圆周运动的向心力 于万有引力，＝mr得＝，图线1的斜率大，则s1‎ 的质量小于s2的质量，故A错误．ρ＝，代入得ρ＝，当r＝R时，ρ＝，由图知r均为R0时，T1>T2，则ρ1<ρ2，故B正确．第一宇宙速度等于近地卫星的绕行速度，由＝m得v＝ ，因M1vB>vC D．要将B卫星转移到A卫星的轨道上运行至少需要对B卫星进行两次加速 ‎【答案】　BD 轨道加速到A卫星的轨道上，选项D正确．‎ ‎【例2】　(2017年天津模拟)中国北斗卫星导航系统(BDS)是中国自主研制的全球卫星导航系统，是继美国全球定位系统(GPS)、俄罗斯格洛纳斯卫星导航系统(GLONASS)之后第三个成熟的卫星导航系统．预计2020年左右，北斗卫星导航系统将形成全球覆盖能力．如图4－2－2所示是北斗导航系统中部分卫星的轨道示意图，已知a、b、c三颗卫星均做圆周运动，a是地球同步卫星，则(　　)‎ A．卫星a的角速度小于c的角速度 B．卫星a的加速度大于b的加速度 C．卫星a的运行速度大于第一宇宙速度 D．卫星b的周期大于24 h ‎【答案】　A 等于a的周期，为24 h，选项D错误． 3 4 ‎ ‎【例3】．理想状态的“日地—拉格朗日点”是指在太阳和地球对人造卫星引力作用下(忽略其他星体引力)，使人造卫星围绕太阳运行的周期与地球围绕太阳运行的周期相同的点．其中两个“日地—拉格朗日点”L1、L2在日地连线上，L1在地球轨道内侧，L2在地球轨道外侧，如图所示，下列说法中正确的是(　　)‎ A．人造卫星在L1处线速度大于地球的线速度 ‎ B．人造卫星在L1处角速度大于地球的角速度 C．人造卫星在L1处加速度小于地球的加速度 D．同一人造卫星在L1处所受万有引力大于在L2处所受万有引力 ‎【答案】C ‎【解析】 由题知“日地—拉格朗日点”是人造卫星绕太阳运行的周期与地球围绕太阳运行的周期相同的点，则人造卫星在L1处和L2处的周期均与地球公转周期相同，由ω＝知人造卫星在L1处角速度等于地球的角速度，故B错误．由v＝ωr知，人造卫星在L1处的线速度小于地球的线速度，故A错误．由a＝ω2r知，人造卫星在L1处加速度小于地球的加速度，故C正确．同一人造卫星在L1处受万有引力等于向心力，L2处受万有引力也等于向心力，由于向心力F＝mω2r，知L1处向心力小于L2处向心力，所以同一人造卫星在L1处所受万有引力小于在L2处所受万有引力，故D错误．‎ 考点三　航天器的变轨追及问题 核心知识 卫星变轨问题 ‎(1) 络结构 ‎(2)卫星在椭圆轨道上的远地点、近地点的加速度与对应圆轨道上的加速度关系应用a＝比较．‎ ‎(3)卫星在同一轨道上稳定运行过程中机械能守恒；在变轨过程中，轨道升高机械能增加，轨道降低机械能减少．‎ 规律方法 卫星变轨问题的有关规律 ‎(1)卫星变轨时速度的变化，根据万有引力和所需向心力的大小关系判断；稳定在新轨道上的运行速度变化由v＝ 判断．‎ ‎(2)航天器在不同轨道上运行时机械能不同，轨道半径越大，机械能越大．‎ ‎(3)航天器经过不同轨道相交的同一点时加速度相等，外轨道的速度大于内轨道的速度．‎ ‎(4)同一轨道对接，应先减速到低轨再加速回高轨，实现与目标航天器对接．‎ 典例分析 ‎【例1】　 (多选)(2017年河南六市高三联考)2009年5月，航天飞机在完成对哈勃空间望远镜的维修任务后，由圆形轨道Ⅰ从A点进入椭圆轨道Ⅱ，B为轨道Ⅱ上的一点，如图所示．关于航天飞机的运动，下列说法中正确的是(　　)‎ A．在轨道Ⅱ上经过A点的速度小于经过B点的速度 B．在轨道Ⅱ上经过A点的速度等于在轨道Ⅰ上经过A点的速度 C．在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期 D．在轨道Ⅱ上经过A点的加速度小于在轨道Ⅰ上经过A点的加速度 ‎【答案】　AC 选项D错误．‎ ‎【例2】　某行星和地球绕太阳公转的轨道均可视为圆．每过N年，该行星会运行到日地连线的延长线上，如图所示．该行星与地球的公转半径之比为(　　)‎ A. 　　　 B. C. 　　　 D. ‎【答案】B ‎【解析】　由开普勒第三定律得r＝ T，r＝ T，所以有＝，由于每过N年，该行星会运行到日地连线的延长线上，即“相遇”，亦即在相同时间内，地球比该行星多转一圈，于是有NT1＝(N－1)T2，联立解得＝. 3 ‎ ‎【例3】(2017年广西四校调研)(多选)“嫦娥三号”发射取得圆满成功，这标志着我国的航空航天技术又迈进了一大步．“嫦娥三号”探月卫星沿地月转移轨道到达距月球表面200 m的P点进行第一次“刹车制动”后被月球捕获，进入椭圆轨道Ⅰ绕月飞行，再经过一次制动进入距月球表面15 m的圆形轨道Ⅱ上绕月球做匀速圆周运动．则下面说法正确的是(　　)‎ A．由于“刹车制动”，卫星沿轨道Ⅱ运动的周期将比沿轨道Ⅰ运动的周期长 B．虽然“刹车制动”，但卫星沿轨道Ⅱ运动的周期比沿轨道Ⅰ运动的周期短 C．卫星在到达月球附近时需进行第一次“刹车制动”，是因为卫星到达月球附近时的速度大于月球的第二宇宙速度 D．卫星沿轨道Ⅱ运动的加速度小于沿轨道Ⅰ运动到P点时的加速度 ‎【答案】BC ‎【例4】‎2017年10月19日“神舟十一号”飞船与“天宫二号”空间实验室自动交会对接成功．假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动，为了实现飞船与空间实验室的对接，下列措施可行的是 (　　)‎ A．使飞船与空间实验室在同一轨道上运行，然后飞船加速追上空间实验室实现对接 B．使飞船与空间实验室在同一轨道上运行，然后空间实验室减速等待飞船实现对接 C．飞船先在比空间实验室半径小的轨道上加速，加速后飞船逐渐靠近空间实验室，两者速度接近时实现对接 D．飞船先在比空间实验室半径小的轨道上减速，减速后飞船逐渐靠近空间实验室，两者速度接近时实现对接 ‎ ‎【答案】C 规律总结 天体相遇问题的解法 围绕同一中心天体做圆周运动的运行天体，因在同一轨道上运行快慢相同不可能相遇(除非是同一轨道上绕行方向相反)，故天体的相遇定义为运行天体A位于运行天体B正上方时，即A、B与中心天体位于同一直线上且A、B在中心天体的同一侧时的状态．‎ 如图甲，当两运行天体A、B的轨道平面在同一平面内时，若运行方向相同，则内侧天体B比A 每多运行一圈时相遇一次，在Δt时间内相遇的次数n＝－＝Δt.若运行方向相反时，则A、B每转过的圆心角之和等于2π时发生一次相遇，在Δt时间内相遇的次数为：n＝＝＋.‎ 如图乙，若两运行天体轨道平面不重合时，当A、B均运行至P、Q所在直线上，且A、B位于同侧时二者才相遇，因此从某次相遇到下次相遇，B比A一定多转1圈，而且A、B各自转的圈数都是半圈的奇数倍，即在Δt时间内，＝(2 A＋1)×，＝(2 B＋1)×，且 B－ A＝1.‎ 考点四　双星及多星问题 核心知识 双星模型 ‎(1)“向心力等大反向”——两颗行星做匀速圆周运动的向心力由它们之间的万有引力提供，故F1＝F2，且方向相反，分别作用在两颗行星上，是一对作用力和反作用力．‎ ‎(2)“周期、角速度相同”——两颗行星做匀速圆周运动的周期、角速度相等．‎ ‎(3)“半径反比”——圆心在两颗行星的连线上，且r1＋r2＝L，两颗行星做匀速圆周运动的半径与行星的质量成反比．‎ 规律方法 双星问题的分析思路和方法 ‎(1)受力分析：双星之间的万有引力提供它们做匀速圆周运动的向心力．‎ ‎(2)轨道分析：双星做匀速圆周运动的圆心是它们连线上的一点，所以双星做匀速圆周运动的半径与双星间的距离是不相等的，它们的轨道半径之和才等于它们间的距离．‎ ‎(3)运动分析：双星属于共轴转动，具有相同的角速度、周期．‎ 典例分析 ‎【例】　(多选)(2017年昆明模拟)宇宙中两颗相距很近的恒星常常组成一个系统，它们以相互间的万有引力彼此提供向心力，从而使它们绕着某一共同的圆心做匀速圆周运动，若已知它们的运转周期为T，两星到某一共同圆心的距离分别为R1和R2，那么，系统中两颗恒星的质量关系是(　　)‎ A．这两颗恒星的质量必定相等 B．这两颗恒星的质量之和为 C．这两颗恒星的质量之比为m1∶m2＝R2∶R1‎ D．其中必有一颗恒星的质量为 ‎【答案】　BC 选项D错误．‎ ‎【例2】．(多选)(2017年济南测试)宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用，设四星系统中每个星体的质量均为m，半径均为R，四颗星稳定分布在边长为a的正方形的四个顶点上，已知引力常量为G.关于宇宙四星系统，下列说法正确的是(　　)‎ A．四颗星围绕正方形对角线的交点做匀速圆周运动 B．四颗星的轨道半径均为 C．四颗星表面的重力加速度均为 D．四颗星的周期均为2πa ‎【答案】ACD ‎2πa ，故D正确． ！ 2 ‎ ‎【例3】.宇宙中存在一些离其他恒星较远，由质量相等的三个星体组成的三星系统，通常可忽略其他星体对它们的引力作用．已观测到稳定的三星系统存在的一种形式是三个星体位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行，如图所示．设每个星体的质量均为m，相邻的两个星体之间的距离为L，引力常量为G，则(　　)‎ ‎ ‎ A．该圆形轨道的半径为L B．每个星体的运行周期均为 C．每个星体做圆周运动的线速度均为 D．每个星体做圆周运动的加速度均与星体的质量无关 ‎ ‎【答案】C ‎【解析】由几何关系得该圆形轨道的半径R＝L，A错误；任意两个星体之间的万有引力F＝，每个星体受到的合力F1＝2Fcos30°，由万有引力定律和牛顿第二定律得cos30°＝mR＝m＝ma，由上式可得T＝2π ，v＝ ，a＝，B、D错误，C正确．‎ ‎【例4】．双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动，研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化，若某双星系统中两星做圆周运动的周期为T，经过一段时间演化后，两星总质量变为原来的 倍，两星之间的距离变为原来的n倍，则此时圆周运动的周期为(　　)‎ A. B.T C.T D.T ‎【答案】B 间距变为原来的n倍时，圆周运动的周期变为 T，B正确． · 1 ‎ 考点总结 ‎1．地球的质量M、半径R、表面的重力加速度g与万有引力恒量G间的关系式为GM＝gR2；7.9 m/s既是人造地球卫星的最大环绕速度也是最小发射速度；人造地球卫星的最小运动周期Tm＝84.8 min≈85 min.‎ ‎2．若行星表面的重力加速度为g，行星的半径为R，则环绕其表面的卫星最低速度为v＝，亦即该行星的第一宇宙速度；若行星的平均密度为ρ，则卫星周期的最小值T与ρ、G之间存在ρT2＝的关系式．‎ ‎3．若已知月球绕地球运行的公转周期T、半径r，则地球的质量为M地＝.‎ ‎4．地球同步卫星(又叫通迅卫星)的六个一定：‎ ‎(1)运转周期一定，即T＝24 h；‎ ‎(2)角速度一定，等于地球自转的角速度；‎ ‎(3)向心加速度大小一定，约为0.23 m/s2；‎ ‎(4)环绕速度大小一定，约为3.08 m/s；‎ ‎(5)轨道平面一定在赤道平面内，即所有的同步卫星都在赤道的正上方，不可能定点在我国某地上空；‎ ‎(6)离地面的高度一定，约为3.59×104 m.‎ ‎5．太空中两个靠近的天体叫“双星”，它们由于万有引力而绕连线上一点做圆周运动，其轨道半径与质量成反比，环绕速度与质量成反比．‎ ‎6．三个宇宙速度是指发射速度、环绕速度和脱离速度．轨道越高发射速度越大，环绕速度越小．‎ ‎7．航天器在同一轨道运行，机械能不变，轨道越高，机械能越大．‎ ‎8．低轨变高轨须加速，高轨回低轨要减速．‎