华大新高考联盟2020届高三1月教学质量测评理科数学 15页

机密★启用前 华大新高考联盟2020届高三1月教学质量测评理科数学 本试题卷共4页，23题（含选考题），全卷满分150分.考试问时120分钟 ‎★祝考试顺利★‎ 注意事项：‎ ‎1.答题前，先将自己的姓名、准考证号填写在答题卡上，并将准考证号条形码贴在答题卡上的指定位置.‎ ‎2.选择题的作答，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题上，草稿纸和答题卡上的非答题区域的无效.‎ ‎3.填空题和解答题的作答，用签字笔直接答在答题卡上对应的答题区域内，写在试题卷，草稿纸和答题卡上的非答题区域均无效.‎ ‎4，选考题的作答，先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑，答案写在答题卡上对应的答题区域内，写在试题卷，草稿纸和答题卡上的非答题区域均无效.‎ ‎5.考试结束后，请将答题卡上交.‎ 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ 1. 已知集合，，则 A. B. C. D.‎ 2. 设复数满足，在复平面内对应的点为，则不可能为 A. B. C. D.‎ 1. 已知，，，则 A. B. C. D.‎ 2. ‎2019年10月1日.为了庆祝中华人民共和国成立70周年，小明、小红、小金三人以国庆为在主题各自独立完成一幅十字绣赠送给当地的村委会，这三幅十字绣分别命名为“鸿福齐天”、“国富民强”、“兴国之路".为了弄清“国富民强”这一作品是谁制作的，村支书对三人进行了同话，得到回复如下： 小明说：“鸿福齐天”是我制作的 小红说：“国富民强”不是小明制作的，就是我制作的 小金说：“兴国之路"不是我制作的. 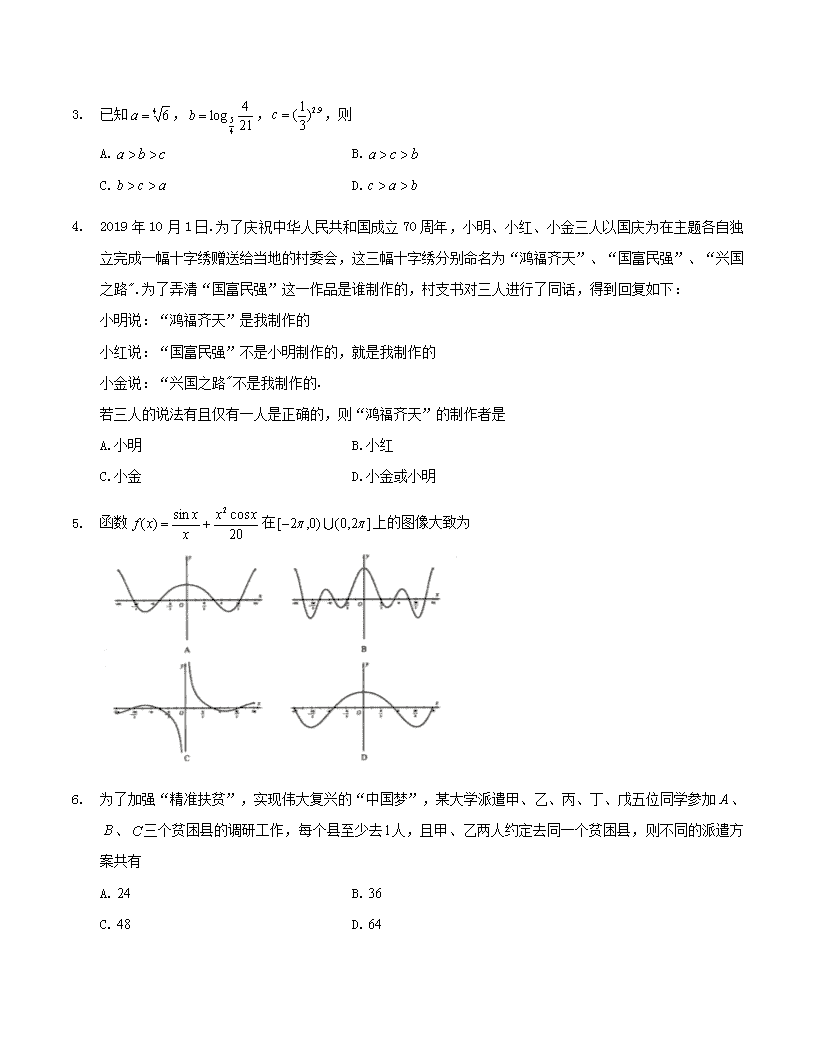若三人的说法有且仅有一人是正确的，则“鸿福齐天”的制作者是 A.小明 B.小红 C.小金 D.小金或小明 3. 函数在上的图像大致为 ‎ 4. 为了加强“精准扶贫”，实现伟大复兴的“中国梦”，某大学派遣甲、乙、丙、丁、戊五位同学参加、、三个贫困县的调研工作，每个县至少去人，且甲、乙两人约定去同一个贫困县，则不同的派遣方案共有 A. B. C. D.‎ 1. 已知向量，，若，则与夹角的余弦值为 A. B. C. D. ‎ 2. 框图与程序是解决数学问题的重要手段，实际生活中的一些问题在抽象为数学模型之后，可以制作框图，编写程序，得到解决.例如，为了计算一姐数据的方差，设计了如图所示的程序框图，其中输入，，，，，，，则图中空白框中应填人 A. B. C. D.‎ 1. 记等差数列的公差为，前项和为，若，，则 A. B. C. D.‎ 2. 已知椭圆：左、右焦点分别为，，点，在椭圆上，其中，，若，，则椭圆的离心率的取值范围为 A. B. C. D.‎ 3. 关于函数，有下述三个结论： ①函数的一个周期为； ②函数在上单词递增； ③函数的值域为. 其中所有正确结论的编号是 A.①② B.② C.②③ D.③‎ 4. 已知四棱锥中，四边形为等腰梯形，，，是等边三角形，且，若点在四棱锥的外接球面上运动，记点到平面的距离为，若平面平面，则的最大值为 A. B. C. D.‎ 二.填空题，本题共4小距.每小题5分，共20分.‎ 1. 已知函数，若曲线在处的切线与直线平行，则__________.‎ 2. 设为数则的前项和，若，则__________.‎ 3. 由于受到网络电商的冲击，某品牌的洗衣机在线下的销售受到影响，承受了一定的经济损失，现将地区家实体店该品牌洗衣机的月经济损失统计如图所示，估算月经济损失的平均数为，中位数为，则__________. ‎ 4. 已知双曲线:的左、右焦点分 别为、，直线是双曲线过第一、三象限的渐近线，记直线的倾斜角为，直线:，，垂足为，若在双曲线上，则双角线的离心率为__________.‎ 三.解答题：共70分，解答应写出文字说明，证明过程或演算步骤，第17-21题为必考题，每个试题考生都必须作答，第22.23题为击考题，考生根据要求作答.‎ ‎（一）必考题，共6分 1. ‎（12分） 已知的内角、、的对边分别为、、，设. （1）求的值； （2）若，且，求的值.‎ 2. ‎（12分） 如图所示，在三棱柱中，为等边三角形，，，平面，是线段上靠近的三等分点. （1）求证：； （2）求直线与平面所成角的正弦值. ‎ 3. ‎（12分） 记抛物线:的焦点为，点，在抛物线上，且直线的斜率为，当直线过点时，. （1）求抛物线的方程； （2）若，直线与交于点，，求直线的斜率.‎ 4. ‎（12分） 已知函数. （1）当 时，求证：； （2）若函数，求证：函数存在极小值.‎ 1. ‎（12分） 为了拓展城市的旅游业，实现不同市区间的物资交流，政府决定在市与市之间建一条直达公路，中间设有至少个的偶数个十字路口，记为，现规划在每个路口处种植一棵杨树或者木棉树，且种植每种树木的概率均为. （1）现征求两市居民的种植意见，看看哪一种植物更受欢迎，得到的数据如下所示： 是否有的把握认为喜欢树木的种类与居民所在的城市具有相关性； （2）若从所有的路口中随机抽取4个路口，恰有个路口种植杨树，求的分布到以及数学期望； （3）在所有的路口种植完成后，选取3个种植同一种树的路口，记总的选取方法数为，求证： . ‎ （二） 选考题：共10分，请考生在第22.23题中任选一题作答，如果多做，则按所做的第一题计分 2. ‎【选修4-4:坐标系与参数方程】（10分） 在平面直角生标系中，曲线的参数方程为（为参数），以原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为. ‎ ‎（1）求曲线的极坐标方程以及曲线的直角坐标方程； （2）若直线与曲线、曲线在第一象限交于、两点，且，点的坐标为，求的面积.‎ 1. ‎【选修4-5：不等式选讲】（10分） 已知，，. （1）求证：； （2）若，求证：.‎