人教A数学必修一指数函数及其性质基础知识讲解 10页

指数函数及其性质 ‎【学习目标】‎ ‎1.掌握指数函数的概念，了解对底数的限制条件的合理性，明确指数函数的定义域；‎ ‎2.掌握指数函数图象：‎ ‎(1)能在基本性质的指导下，用列表描点法画出指数函数的图象，能从数形两方面认识指数函数的性质；‎ ‎(2)掌握底数对指数函数图象的影响；‎ ‎(3)从图象上体会指数增长与直线上升的区别．‎ ‎3.学会利用指数函数单调性来比较大小，包括较为复杂的含字母讨论的类型；‎ ‎4.通过对指数函数的概念、图象、性质的学习，培养观察、分析归纳的能力，进一步体会数形结合的思想方法；‎ ‎5.通过对指数函数的研究，要认识到数学的应用价值，更善于从现实生活中发现问题，解决问题．‎ ‎【要点梳理】‎ 要点一、指数函数的概念：‎ 函数y=ax(a>0且a≠1)叫做指数函数，其中x是自变量，a为常数，函数定义域为R.‎ 要点诠释：‎ ‎（1）形式上的严格性：只有形如y=ax(a>0且a≠1)的函数才是指数函数．像，，等函数都不是指数函数．‎ ‎（2）为什么规定底数a大于零且不等于1：‎ ‎①如果，则 ‎②如果，则对于一些函数，比如，当时，在实数范围内函数值不存在．‎ ‎③如果，则是个常量，就没研究的必要了．‎ 要点二、指数函数的图象及性质：‎ y=ax ‎01时图象 图象 性质 ‎①定义域R，值域 （0，+∞）‎ ‎②a0=1, 即x=0时，y=1，图象都经过(0，1)点 ‎③ax=a，即x=1时，y等于底数a ‎④在定义域上是单调减函数 ‎④在定义域上是单调增函数 ‎⑤x<0时，ax>1‎ x>0时，00时，ax>1‎ ‎⑥ 既不是奇函数，也不是偶函数 要点诠释：‎ ‎（1）当底数大小不定时，必须分“”和“”两种情形讨论。‎ ‎（2）当时，；当时。‎ 当时，的值越大，图象越靠近轴，递增速度越快。‎ 当时，的值越小，图象越靠近轴，递减的速度越快。‎ ‎（3）指数函数与的图象关于轴对称。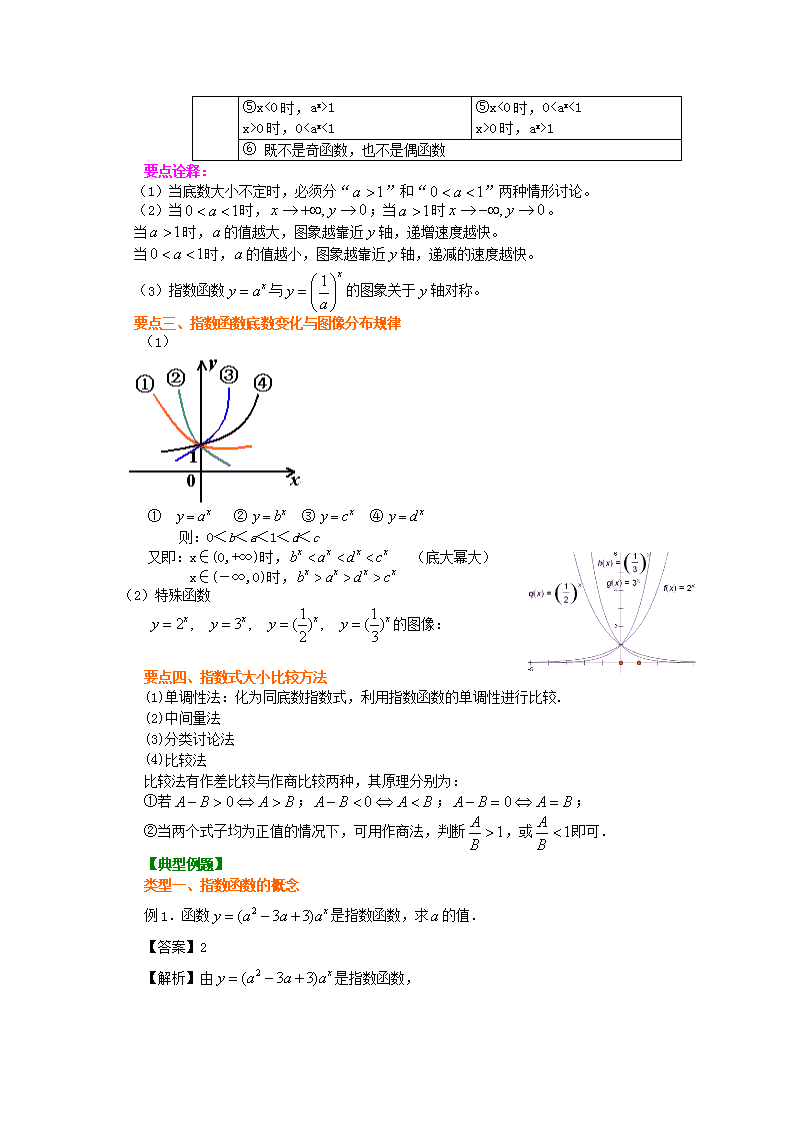‎ 要点三、指数函数底数变化与图像分布规律 ‎（1）‎ ① ‎ ② ③ ④ ‎ ‎ 则：0＜b＜a＜1＜d＜c 又即：x∈(0,+∞)时， （底大幂大）‎ ‎ x∈(－∞,0)时，‎ ‎（2）特殊函数 的图像：‎ 要点四、指数式大小比较方法 ‎(1)单调性法：化为同底数指数式，利用指数函数的单调性进行比较.‎ ‎(2)中间量法 ‎(3)分类讨论法 ‎(4)比较法 比较法有作差比较与作商比较两种，其原理分别为：‎ ‎①若；；；‎ ‎②当两个式子均为正值的情况下，可用作商法，判断，或即可．‎ ‎【典型例题】‎ 类型一、指数函数的概念 例1．函数是指数函数，求的值．‎ ‎【答案】2‎ ‎【解析】由是指数函数，‎ 可得解得，所以．‎ ‎【总结升华】判断一个函数是否为指数函数：‎ ‎（1）切入点：利用指数函数的定义来判断；‎ ‎（2）关键点：一个函数是指数函数要求系数为1，底数是大于0且不等于1的常数，指数必须是自变量．‎ 举一反三：‎ ‎【变式1】指出下列函数哪些是指数函数？‎ ‎（1）；（2）；（3）；（4）；‎ ‎（5）；（6）．‎ ‎【答案】（1）（5）（6）‎ ‎【解析】（1）（5）（6）为指数函数．其中（6）=，符合指数函数的定义，而（2）中底数不是常数，而4不是变数；（3）是-1与指数函数的乘积；（4）中底数，所以不是指数函数．‎ 类型二、函数的定义域、值域 例2．求下列函数的定义域、值域.‎ ‎(1)；(2)y=4x-2x+1；(3)；(4)(a为大于1的常数)‎ ‎【答案】（1）R，(0，1)；（2）R [)；（3） ；（4）(-∞，-1)∪[1，+∞) ‎ ‎[1，a)∪(a，+∞)‎ ‎【解析】(1)函数的定义域为R (∵对一切xR，3x≠-1).‎ ‎∵ ，又∵ 3x>0， 1+3x>1，‎ ‎∴ ， ∴ ，‎ ‎∴ ， ∴值域为(0，1).‎ ‎(2)定义域为R，，∵ 2x>0， ∴ 即 x=-1时，y取最小值，同时y可以取一切大于的实数，∴ 值域为[).‎ ‎(3)要使函数有意义可得到不等式，即，又函数是增函数，所以，即，即，值域是.‎ ‎(4)∵ ∴ 定义域为(-∞，-1)∪[1，+∞)，‎ 又∵ ，∴ ， ∴值域为[1，a)∪(a，+∞).‎ ‎【总结升华】求值域时有时要用到函数单调性；第(3)小题中值域切记不要漏掉y>0的条件，第(4)小题中不能遗漏.‎ 举一反三：‎ ‎【变式1】求下列函数的定义域：‎ ‎(1) (2)‎ ‎(3) (4)‎ ‎【答案】（1）R；（2）；（3）；（4）a>1时，；01时，；01时，外层函数y=au在上为增函数，内函数u=x2-2x在区间上为减函数，在区间上为增函数，故函数上为减函数，在区间上为增函数；‎ 当01， x11且x2-x1>0，‎ ‎∴， ∴ .‎ ‎【总结升华】指数函数是学习了函数的一般性质后，所学的第一个具体函数.因此，在学习中，尽量体会从一般到特殊的过程.‎ 例5．判断下列各数的大小关系：‎ ‎(1)‎1.8a与‎1.8a+1； (2) ‎ ‎(3)22.5，(2.5)0， (4)‎ ‎【思路点拨】利用指数函数的性质去比较大小。‎ ‎【答案】（1）‎1.8a<‎1.8a+1 （2） （3）‎ ‎（4）当a>1时，，当01，所以函数y=1.8x为单调增函数，‎ 又因为a1时，，当01，‎ ‎ 1.1>1， -0.1<0Þ0<1.1-0.1<1， 则0.9-0.3>1.1-0.1；‎ ‎(4)由指数函数图象相对位置关系——数形结合，0.90.3>0.70.4.‎ ‎(5)∵，又函数为减函数，‎ ‎， ∴ ，‎ ‎∵为增函数，时，y>1，.‎ 另解：幂函数为增函数，则有，(下略).‎ ‎【高清课堂：指数函数 369066 例1】‎ ‎【变式2】利用函数的性质比较，，‎ ‎【答案】‎ ‎【解析】=‎ ‎ ‎ ‎ 作出的图象知 ‎ ‎ ‎ 所以 ‎【变式3】 比较1.5-0.2， ‎1.30.7‎， 的大小.‎ ‎【答案】‎ ‎【解析】先比较的大小.由于底数(0，1)， ∴ 在R上是减函数，∵ ， ∴ ，再考虑指数函数y=1.3x， 由于1.3>1， 所以y=1.3x在R上为增函数‎1.30.7‎>1.30=1， ∴ .‎ ‎【总结升华】在进行数的大小比较时，若底数相同，则可根据指数函数的性质得出结果，若底数不相同，则首先考虑能否化成同底数，然后根据指数函数的性质得出结果；不能化成同底数的，要考虑引进第三个数(如0，1等)分别与之比较，从而得出结果.总之比较时要尽量转化成底的形式，根据指数函数单调性进行判断.‎ 例6. (分类讨论指数函数的单调性)化简：‎ ‎【思路点拨】先把被开方数变形成完全平方式的形式，然后对进行分类讨论，去掉绝对值。‎ ‎【解析】‎ 举一反三：‎ ‎【变式1】如果（，且），求的取值范围．‎ ‎【答案】当时，；当时，‎ ‎【解析】（1）当时，由于，‎ ‎，解得．‎ ‎（2）当时，由于，‎ ‎，解得．‎ 综上所述，的取值范围是：当时，；当时，．‎ 类型四、判断函数的奇偶性 例7．判断下列函数的奇偶性： (为奇函数)‎ ‎【答案】偶函数 ‎【解析】f(x)定义域关于原点对称(∵定义域关于原点对称，且f(x)的定义域是定义域除掉0这个元素)，令，则 ‎∴ g(x)为奇函数， 又 ∵为奇函数，∴ f(x)为偶函数.‎ ‎【总结升华】求的奇偶性，可以先判断与的奇偶性，然后在根据奇·奇=偶，偶·偶=偶，奇·偶=奇，得出的奇偶性．‎ 举一反三：‎ ‎【变式1】判断函数的奇偶性：.‎ ‎【答案】偶函数 ‎【解析】定义域{x|xR且x≠0}，‎ 又 ‎ ， ‎ ‎∴ f(-x)=f(x)，则f(x)偶函数.‎ 类型五、指数函数的图象问题 例8．如图的曲线C1、C2、C3、C4是指数函数的图象，而，则图象C1、C2、C3、C4对应的函数的底数依次是________、________、________、________．‎ ‎【答案】 ‎ ‎【解析】由底数变化引起指数函数图象的变化规律可知，C2的底数＜C1的底数＜C4的底数＜C3的底数．‎ ‎【总结升华】利用底数与指数函数图象之间的关系可以快速地解答像本题这样的有关问题，同时还可以解决有关不同底的幂的大小比较的问题，因此我们必须熟练掌握这一性质，这一性质可简单地记作：在y轴的右边“底大图高”，在y轴的左边“底大图低”．‎ 举一反三：‎ ‎【变式1】 设，c＜b＜a且，则下列关系式中一定成立的是（ ）‎ A． B． C． D．‎ ‎ 【答案】D ‎【变式2】为了得到函数的图象，可以把函数的图象(　　)‎ A．向左平移9个单位长度，再向上平移5个单位长度 B．向右平移9个单位长度，再向下平移5个单位长度 C．向左平移2个单位长度，再向上平移5个单位长度 D．向右平移2个单位长度，再向下平移5个单位长度 ‎【答案】C ‎【解析】注意先将函数转化为，再利用图象的平移规律进行判断．‎ ‎∵，∴把函数的图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数的图象，故选C．‎ ‎【总结升华】用函数图象解决问题是中学数学的重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数的图象，并掌握图象的变化规律，比如：平移、伸缩、对称等．‎