2018年河南省郑州市高考数学一模试卷（文科） 25页

‎2018年河南省郑州市高考数学一模试卷（文科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）复数（i为虚数单位）等于（　　）‎ A．﹣1﹣3i B．﹣1+3i C．1﹣3i D．1+3i ‎2．（5分）设集合A={x|1＜x＜2}，B={x|x＜a}，若A∩B=A，则a的取值范围是（　　）‎ A．{a|a≤2} B．{a|a≤1} C．{a|a≥1} D．{a|a≥2}‎ ‎3．（5分）设向量=（1，m），=（m﹣1，2），且≠，若（﹣）⊥，则实数m=（　　）‎ A．2 B．1 C． D．‎ ‎4．（5分）下列说法正确的是（　　）‎ A．“若a＞1，则a2＞1”的否命题是“若a＞1，则a2≤1”‎ B．“若am2＜bm2，则a＜b”的逆命题为真命题 C．∃x0∈（0，+∞），使成立 D．“若，则”是真命题 ‎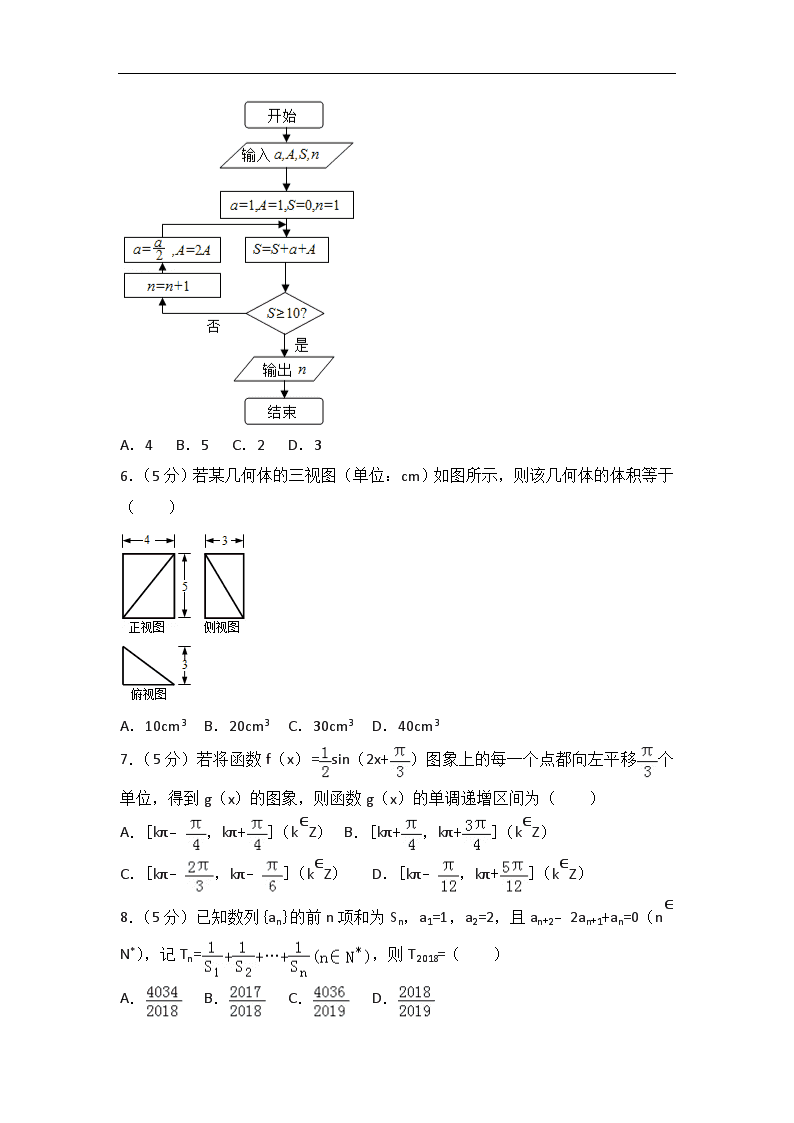5．（5分）我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n=（　　）‎ A．4 B．5 C．2 D．3‎ ‎6．（5分）若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（　　）‎ A．10cm3 B．20cm3　 C．30cm3 D．40cm3‎ ‎7．（5分）若将函数f（x）=sin（2x+）图象上的每一个点都向左平移个单位，得到g（x）的图象，则函数g（x）的单调递增区间为（　　）‎ A．[kπ﹣，kπ+]（k∈Z） B．[kπ+，kπ+]（k∈Z）‎ C．[kπ﹣，kπ﹣]（k∈Z） D．[kπ﹣，kπ+]（k∈Z）‎ ‎8．（5分）已知数列{an}的前n项和为Sn，a1=1，a2=2，且an+2﹣2an+1+an=0（n∈N*），记Tn=，则T2018=（　　）‎ A． B． C． D．‎ ‎9．（5分）已知函数，若函数f（x）在R上有两个零点，则实数a的取值范围是（　　）‎ A．（0，1] B．[1，+∞） C．（0，1） D．（﹣∞，1]‎ ‎10．（5分）已知椭圆的左顶点和上顶点分别为A，B，左、右焦点分别是F1，F2，在线段AB上有且只有一个点P满足PF1⊥PF2，则椭圆的离心率的平方为（　　）‎ A． B． C． D．‎ ‎11．（5分）我市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学联赛（河南初赛），他们取得的成绩（满分140分）的茎叶图如图所示，其中甲班学生成绩的中位数是81，乙班学生成绩的平均数是86，若正实数a，b满足a，G，b成等差数列且x，G，y成等比数列，则的最小值为（　　）‎ A． B．2 C． D．9‎ ‎12．（5分）若对于任意的正实数x，y都有成立，则实数m的取值范围为（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（本题共4小题，每题5分，共20分）‎ ‎13．（5分）设变量x，y满足约束条件则目标函数z=4x﹣y的最小值为　 　．‎ ‎14．（5分）如果直线ax+2y+3a=0与直线3x+（a﹣1）y=a﹣7平行，则a=　 　．‎ ‎15．（5分）已知数列{an}满足，且a1+a2+a3+…+a10=1，则log2（a101+a102+…+a110）=　 　．‎ ‎16．（5分）已知双曲线的右焦点为F，过点F向双曲线的一条渐近线引垂线，垂足为M，交另一条渐近线于N，若，则双曲线的渐近线方程为　 　．‎ ‎　‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17．（12分）在△ABC中，角A，B，C的对边分别为a，b，c，且2ccosB=2a+b．‎ ‎（1）求角C；‎ ‎（2）若△ABC的面积为，求ab的最小值．‎ ‎18．（12分）2017年10月份郑州市进行了高三学生的体育学业水平测试，为了考察高中学生的身体素质比情况，现抽取了某校1000名（男生800名，女生200名）学生的测试成绩，根据性别按分层抽样的方法抽取100名进行分析，得到如下统计图表：‎ 男生测试情况：‎ 抽样情况 病残免试 不合格 合格 良好 优秀 人数 ‎5‎ ‎10‎ ‎15‎ ‎47‎ x 女生测试情况 抽样情况 病残免试 不合格 合格 良好 优秀 人数 ‎2‎ ‎3‎ ‎10‎ y ‎2‎ ‎（1）现从抽取的1000名且测试等级为“优秀”的学生中随机选出两名学生，求选出的这两名学生恰好是一男一女的概率；‎ ‎（2）若测试等级为“良好”或“优秀”的学生为“体育达人”，其它等级的学生（含病残免试）为“非体育达人”，根据以上统计数据填写下面列联表，并回答能否在犯错误的概率不超过0.010的前提下认为“是否为体育达人”与性别有关？‎ 男性 女性 总计 体育达人 非体育达人 总计 临界值表：‎ P（K2≥k0）‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ k0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ 附：（，其中n=a+b+c+d）‎ ‎19．（12分）如图，在三棱锥P﹣ABC中，平面PAB⊥平面ABC，AB=6，，，D，E为线段AB上的点，且AD=2DB，PD⊥AC．‎ ‎（1）求证：PD⊥平面ABC；‎ ‎（2）若，求点B到平面PAC的距离．‎ ‎20．（12分）已知圆C：x2+y2+2x﹣2y+1=0和抛物线E：y2=2px（p＞0），圆心C到抛物线焦点F的距离为．‎ ‎（1）求抛物线E的方程；‎ ‎（2）不过原点的动直线l交抛物线于A，B两点，且满足OA⊥OB．设点M为圆C上任意一动点，求当动点M到直线l的距离最大时的直线l方程．‎ ‎21．（12分）已知函数f（x）=lnx﹣a（x+1），a∈R在（1，f（1））处的切线与x轴平行．‎ ‎（1）求f（x）的单调区间；‎ ‎（2）若存在x0＞1，当x∈（1，x0）时，恒有成立，求k的取值范围．‎ ‎22．（10分）在平面直角坐标系xOy中，直线l过点（1，0），倾斜角为α，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程是．‎ ‎（1）写出直线l的参数方程和曲线C的直角坐标方程；‎ ‎（2）若，设直线l与曲线C交于A，B两点，求△AOB的面积．‎ ‎23．设函数f（x）=|x+3|，g（x）=|2x﹣1|．‎ ‎（1）解不等式f（x）＜g（x）；‎ ‎（2）若2f（x）+g（x）＞ax+4对任意的实数x恒成立，求a的取值范围．‎ ‎　‎ ‎2018年河南省郑州市高考数学一模试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）复数（i为虚数单位）等于（　　）‎ A．﹣1﹣3i B．﹣1+3i C．1﹣3i D．1+3i ‎【解答】解：==﹣1﹣3i 故选A ‎　‎ ‎2．（5分）设集合A={x|1＜x＜2}，B={x|x＜a}，若A∩B=A，则a的取值范围是（　　）‎ A．{a|a≤2} B．{a|a≤1} C．{a|a≥1} D．{a|a≥2}‎ ‎【解答】解：∵A∩B=A，‎ ‎∴A⊆B．‎ ‎∵集合A={x|1＜x＜2}，B={x|x＜a}，‎ ‎∴a≥2‎ 故选：D．‎ ‎　‎ ‎3．（5分）设向量=（1，m），=（m﹣1，2），且≠，若（﹣）⊥，则实数m=（　　）‎ A．2 B．1 C． D．‎ ‎【解答】解：∵（﹣）⊥，‎ ‎∴（﹣）•=0，‎ 即2﹣•=0，‎ 即1+m2﹣（m﹣1+2m）=0，‎ 即m2﹣3m+2=0，‎ 得m=1或m=2，‎ 当m=1时，量=（1，1），=（0，2），满足≠，‎ 当m=2时，量=（1，2），=（1，2），不满足≠，‎ 综上m=1，‎ 故选：B．‎ ‎　‎ ‎4．（5分）下列说法正确的是（　　）‎ A．“若a＞1，则a2＞1”的否命题是“若a＞1，则a2≤1”‎ B．“若am2＜bm2，则a＜b”的逆命题为真命题 C．∃x0∈（0，+∞），使成立 D．“若，则”是真命题 ‎【解答】解：“若a＞1，则a2＞1”的否命题是“若a≤1，则a2≤1”，故A错；‎ ‎“若am2＜bm2，则a＜b”的逆命题为假命题，比如m=0，若a＜b，则am2=bm2，故B错；‎ 对任意x＞0，均有3x＜4x成立，故C错；‎ 对若，则”的逆否命题是“若α=，则sinα=”为真命题，‎ 则D正确．‎ 故选D．‎ ‎　‎ ‎5．（5分）我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n=（　　）‎ A．4 B．5 C．2 D．3‎ ‎【解答】解：模拟执行程序，可得 a=1，A=1，S=0，n=1‎ S=2‎ 不满足条件S≥10，执行循环体，n=2，a=，A=2，S=‎ 不满足条件S≥10，执行循环体，n=3，a=，A=4，S=‎ 不满足条件S≥10，执行循环体，n=4，a=，A=8，S=‎ 满足条件S≥10，退出循环，输出n的值为4．‎ 故选：A．‎ ‎　‎ ‎6．（5分）若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（　　）‎ A．10cm3 B．20cm3　 C．30cm3 D．40cm3‎ ‎【解答】解：由三视图知几何体为三棱柱削去一个三棱锥如图：‎ 棱柱的高为5；底面为直角三角形，直角三角形的直角边长分别为3、4，‎ ‎∴几何体的体积V=×3×4×5﹣××3×4×5=20（cm3）．‎ 故选B．‎ ‎　‎ ‎7．（5分）若将函数f（x）=sin（2x+）图象上的每一个点都向左平移个单位，得到g（x）的图象，则函数g（x）的单调递增区间为（　　）‎ A．[kπ﹣，kπ+]（k∈Z） B．[kπ+，kπ+]（k∈Z）‎ C．[kπ﹣，kπ﹣]（k∈Z） D．[kπ﹣，kπ+]（k∈Z）‎ ‎【解答】解：将函数f（x）=sin（2x+）图象上的每一个点都向左平移个单位，得到g（x）=sin[2（x+）+]=﹣sin2x的图象，‎ 故本题即求y=sin2x的减区间，令2kπ+≤2x≤2kπ+，求得kπ+≤x≤kπ+，‎ 故函数g（x）的单调递增区间为[kπ+，kπ+]，k∈Z，‎ 故选：B．‎ ‎　‎ ‎8．（5分）已知数列{an}的前n项和为Sn，a1=1，a2=2，且an+2﹣2an+1+an=0（n∈N*），记Tn=，则T2018=（　　）‎ A． B． C． D．‎ ‎【解答】解：数列{an}的前n项和为Sn，a1=1，a2=2，且an+2﹣2an+1+an=0（n∈‎ N*），‎ 则：数列为等差数列．‎ 设公差为d，则：d=a2﹣a1=2﹣1=1，‎ 则：an=1+n﹣1=n．‎ 故：，‎ 则：，‎ 所以：，‎ ‎=，‎ ‎=，‎ ‎=．‎ 所以：．‎ 故选：C ‎　‎ ‎9．（5分）已知函数，若函数f（x）在R上有两个零点，则实数a的取值范围是（　　）‎ A．（0，1] B．[1，+∞） C．（0，1） D．（﹣∞，1]‎ ‎【解答】解：当x≤0时，f（x）单调递增，∴f（x）≤f（0）=1﹣a，‎ 当x＞0时，f（x）单调递增，且f（x）＞﹣a．‎ ‎∵f（x）在R上有两个零点，‎ ‎∴，解得0＜a≤1．‎ 故选A．‎ ‎　‎ ‎10．（5分）已知椭圆 的左顶点和上顶点分别为A，B，左、右焦点分别是F1，F2，在线段AB上有且只有一个点P满足PF1⊥PF2，则椭圆的离心率的平方为（　　）‎ A． B． C． D．‎ ‎【解答】解：方法一：依题意，作图如下：A（﹣a，0），B（0，b），F1（﹣c，0），F2（c，0），‎ ‎∴直线AB的方程为，整理得：bx﹣ay+ab=0，设直线AB上的点P（x，y），‎ 则bx=ay﹣ab，x=y﹣a，‎ ‎∵PF1⊥PF2，则•=（﹣c﹣x，﹣y）•（c﹣x，﹣y）=x2+y2﹣c2=（）2+y2﹣c2，‎ 令f（y）=（）2+y2﹣c2，则f′（y）=2（y﹣a）×+2y，‎ ‎∴由f′（y）=0得：y=，于是x=﹣，‎ ‎∴•=（﹣）2+（）2﹣c2=0，‎ 整理得：=c2，又b2=a2﹣c2，整理得：c4+3c2c2﹣a4=0，两边同时除以a4，‎ 由e2=，∴e4﹣3e2+1=0，∴e2=，又椭圆的离心率e∈（0，1），‎ ‎∴e2=．‎ 椭圆的离心率的平方，‎ 故选B．‎ 方法二：由直线AB的方程为，整理得：bx﹣ay+ab=0，‎ 由题意可知：直线AB与圆O：x2+y2=c2相切，‎ 可得d==c，两边平方，整理得：c4+3c2c2﹣a4=0，两边同时除以a4，由e2=，e4﹣3e2+1=0，‎ ‎∴e2=，又椭圆的离心率e∈（0，1），∴e2=．‎ 椭圆的离心率的平方，‎ 故选B．‎ ‎　‎ ‎11．（5分）我市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学联赛（河南初赛），他们取得的成绩（满分140分）的茎叶图如图所示，其中甲班学生成绩的中位数是81，乙班学生成绩的平均数是86，若正实数a，b满足a，G，b成等差数列且x，G，y成等比数列，则的最小值为（　　）‎ A． B．2 C． D．9‎ ‎【解答】解：甲班学生成绩的中位数是80+x=81，得x=1；‎ 由茎叶图可知乙班学生的总分为76+80×3+90×3+（0+2+y+1+3+6）=598+y，‎ 乙班学生的平均分是86，且总分为86×7=602，所以y=4，‎ 若正实数a、b满足：a，G，b成等差数列且x，G，y成等比数列，‎ 则xy=G2，2G=a+b，即有a+b=4，a＞0，b＞0，‎ 则+=（a+b）（+）=（1+4++）≥（5+2）=×9=，‎ 当且仅当b=2a=时，的最小值为．‎ ‎　‎ ‎12．（5分）若对于任意的正实数x，y都有成立，则实数m的取值范围为（　　）‎ A． B． C． D．‎ ‎【解答】解：根据题意，对于（2x﹣）•ln≤，变形可得（2x﹣）ln≤，‎ 即（2e﹣）ln≤，‎ 设t=，则（2e﹣t）lnt≤，t＞0，‎ 设f（t）=（2e﹣t）lnt，（t＞0）‎ 则其导数f′（t）=﹣lnt+﹣1，‎ 又由t＞0，则f′（t）为减函数，且f′（e）=﹣lne+﹣1=0，‎ 则当t∈（0，e）时，f′（t）＞0，f（t）为增函数，‎ 当t∈（e，+∞）时，f′（t）＜0，f（t）为减函数，‎ 则f（t）的最大值为f（e），且f（e）=e，‎ 若f（t）=（2e﹣t）lnt≤恒成立，必有e≤，‎ 解可得0＜m≤，即m的取值范围为（0，]；‎ 故选：D．‎ ‎　‎ 二、填空题（本题共4小题，每题5分，共20分）‎ ‎13．（5分）设变量x，y满足约束条件则目标函数z=4x﹣y的最小值为　1　．‎ ‎【解答】解：设变量x，y满足约束条件在坐标系中画出可行域三角形，‎ 平移直线4x﹣y=0经过点A（1，3）时，4x﹣y最小，最小值为：1，‎ 则目标函数z=4x﹣y的最小值：1．‎ 故答案为：1．‎ ‎　‎ ‎14．（5分）如果直线ax+2y+3a=0与直线3x+（a﹣1）y=a﹣7平行，则a=　3　．‎ ‎【解答】解：∵直线ax+2y+3a=0与直线3x+（a﹣1）y=a﹣7平行，‎ ‎∴，‎ 解得a=3．‎ 故答案为：3．‎ ‎　‎ ‎15．（5分）已知数列{an}满足，且a1+a2+a3+…+a10=1，则log2（a101+a102+…+a110）=　100　．‎ ‎【解答】解：∵，‎ ‎∴log2an+1﹣log2an=1，即，‎ ‎∴．‎ ‎∴数列{an}是公比q=2的等比数列．‎ 则a101+a102+…+a110=（a1+a2+a3+…+a10）q100=2100，‎ ‎∴log2（a101+a102+…+a110）=．‎ 故答案为：100．‎ ‎　‎ ‎16．（5分）已知双曲线的右焦点为F，过点F向双曲线的一条渐近线引垂线，垂足为M，交另一条渐近线于N，若，则双曲线的渐近线方程为　y=±x　．‎ ‎【解答】解：由题意得右焦点F（c，0），‎ 设一渐近线OM的方程为y=x，‎ 则另一渐近线ON的方程为y=﹣x，‎ 由FM的方程为y=﹣（x﹣c），‎ 联立方程y=x，‎ 可得M的横坐标为，‎ 由FM的方程为y=﹣（x﹣c），联立方程y=﹣x，‎ 可得N的横坐标为．‎ 由2=，‎ 可得2（﹣c）=﹣c，‎ 即为﹣c=，‎ 由e=，可得﹣1=，‎ 即有e4﹣5e2+4=0，解得e2=4或1（舍去），‎ 即为e=2，即c=2a，b=a，‎ 可得渐近线方程为y=±x，‎ 故答案为：y=±x．‎ ‎　‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17．（12分）在△ABC中，角A，B，C的对边分别为a，b，c，且2ccosB=2a+b．‎ ‎（1）求角C；‎ ‎（2）若△ABC的面积为，求ab的最小值．‎ ‎【解答】解：（1）由正弦定理可知：===2R，a=2RsinA，b=2RsinB，c=2RsinC，‎ 由2ccosB=2a+b，则2sinCcosB=2sin（B+C）+sinB，‎ ‎∴2sinBcosC+sinB=0，‎ 由0＜B＜π，sinB≠0，cosC=﹣，‎ ‎0＜C＜π，则C=；‎ ‎（2）由S=absinC=c，则c=ab，‎ 由c2=a2+b2﹣2abcosC=a2+b2+ab，∴=a2+b2+ab≥3ab，‎ 当且仅当a=b时取等号，‎ ‎∴ab≥12，‎ 故ab的最小值为12．‎ ‎　‎ ‎18．（12分）2017年10月份郑州市进行了高三学生的体育学业水平测试，为了考察高中学生的身体素质比情况，现抽取了某校1000名（男生800名，女生200名）学生的测试成绩，根据性别按分层抽样的方法抽取100名进行分析，得到如下统计图表：‎ 男生测试情况：‎ 抽样情况 病残免试 不合格 合格 良好 优秀 人数 ‎5‎ ‎10‎ ‎15‎ ‎47‎ x 女生测试情况 抽样情况 病残免试 不合格 合格 良好 优秀 人数 ‎2‎ ‎3‎ ‎10‎ y ‎2‎ ‎（1）现从抽取的1000名且测试等级为“优秀”的学生中随机选出两名学生，求选出的这两名学生恰好是一男一女的概率；‎ ‎（2）若测试等级为“良好”或“优秀”的学生为“体育达人”，其它等级的学生（含病残免试）为“非体育达人”，根据以上统计数据填写下面列联表，并回答能否在犯错误的概率不超过0.010的前提下认为“是否为体育达人”与性别有关？‎ 男性 女性 总计 体育达人 非体育达人 总计 临界值表：‎ P（K2≥k0）‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ k0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ 附：（，其中n=a+b+c+d）‎ ‎【解答】解：（1）按分层抽样男生应抽取80名，女生应抽取20名；‎ ‎∴x=80﹣（5+10+15+47）=3，‎ y=20﹣（2+3+10+2）=3；‎ 抽取的100名且测试等级为优秀的学生中有三位男生，设为A，B，C；‎ 两位女生设为a，b；从5名任意选2名，总的基本事件有 AB，AC，Aa，Ab，BC，Ba，Bb，Ca，Cb，ab，共10个；‎ 设“选出的两名学生恰好是一男一女为事件A”；‎ 则事件包含的基本事件有Aa，Ab，Ba，Bb，Ca，Cb共6个；‎ ‎∴P（A）==；‎ ‎（2）填写2×2列联表如下：‎ 男生 女生 总计 体育达人 ‎50‎ ‎5‎ ‎55‎ 非体育达人 ‎30‎ ‎15‎ ‎45‎ 总计 ‎80‎ ‎20‎ ‎100‎ 则K2=≈9.091；‎ ‎∵9.091＞6.635且P（K2≥6.635）=0.010，‎ ‎∴在犯错误的概率不超过0.010的前提下认为“是否为‘体育达人’与性别有关”．‎ ‎　‎ ‎19．（12分）如图，在三棱锥P﹣ABC中，平面PAB⊥平面ABC，AB=6，，，D，E为线段AB上的点，且AD=2DB，PD⊥AC．‎ ‎（1）求证：PD⊥平面ABC；‎ ‎（2）若，求点B到平面PAC的距离．‎ ‎【解答】证明：（1）连接CD，据题知AD=4，BD=2，‎ ‎∵AC2+BC2=AB2，∴∠ACB=90°，∴cos，‎ ‎∴=8，∴CD=2，‎ ‎∴CD2+AD2=AC2，∴CD⊥AB，‎ 又∵平面PAB⊥平面ABC，∴CD⊥平面PAB，∴CD⊥PD，‎ ‎∵PD⊥AC，CD∩AC=C，∴PD⊥平面ABC．‎ 解：（2）∵，∴PD=AD=4，∴PA=4，‎ 在Rt△PCD中，PC==2，‎ ‎∴△PAC是等腰三角形，∴，‎ 设点B到平面PAC的距离为d，‎ 由VE﹣PAC=VP﹣AEC，得，‎ ‎∴d==3，‎ 故点B到平面PAC的距离为3．‎ ‎　‎ ‎20．（12分）已知圆C：x2+y2+2x﹣2y+1=0和抛物线E：y2=2px（p＞0），圆心C到抛物线焦点F的距离为．‎ ‎（1）求抛物线E的方程；‎ ‎（2）不过原点的动直线l交抛物线于A，B两点，且满足OA⊥OB．设点M为圆C上任意一动点，求当动点M到直线l的距离最大时的直线l方程．‎ ‎【解答】解：（1）圆C：x2+y2+2x﹣2y+1=0可化为（x+1）2+（y﹣1）2=1，‎ 则圆心为（﹣1，1）．‎ 抛物线E：y2=2px（p＞0），焦点坐标F（），‎ 由于：圆心C到抛物线焦点F的距离为．‎ 则：，‎ 解得：p=6．‎ 故抛物线的方程为：y2=12x ‎（2）设直线的方程为x=my+t，A（x1，y1），B（x2，y2），‎ 则：，‎ 整理得：y2﹣12my﹣12t=0，‎ 所以：y1+y2=12m，y1y2=﹣12t．‎ 由于：OA⊥OB．‎ 则：x1x2+y1y2=0．‎ 即：（m2+1）y1y2+mt（y1+y2）+t2=0．‎ 整理得：t2﹣12t=0，‎ 由于t≠0，‎ 解得t=12．‎ 故直线的方程为x=my+12，‎ 直线经过定点（12，0）．‎ 当CN⊥l时，即动点M经过圆心C（﹣1，1）时到直线的距离取最大值．‎ 当CP⊥l时，即动点M经过圆心C（﹣1，1）时到动直线L的距离取得最大值．‎ kMP=kCP=﹣，‎ 则：m=．‎ 此时直线的方程为：x=，‎ 即：13x﹣y﹣156=0．‎ ‎　‎ ‎21．（12分）已知函数f（x）=lnx﹣a（x+1），a∈R在（1，f（1））处的切线与x轴平行．‎ ‎（1）求f（x）的单调区间；‎ ‎（2）若存在x0＞1，当x∈（1，x0）时，恒有成立，求k的取值范围．‎ ‎【解答】解：（1）由已知可得f（x）的定义域为（0，+∞），‎ ‎∵f′（x）=﹣a，∴f′（1）=1﹣a=0，解得：a=1，‎ ‎∴f′（x）=，‎ 令f′（x）＞0，解得：0＜x＜1，令f′（x）＜0，解得：x＞1，‎ 故f（x）在（0，1）递增，在（1，+∞）递减；‎ ‎（1）不等式f（x）﹣+2x+＞k（x﹣1）‎ 可化为lnx﹣+x﹣＞k（x﹣1），‎ 令g（x）=lnx﹣+x﹣﹣k（x﹣1），（x＞1），‎ g′（x）=，‎ ‎∵x＞1，令h（x）=﹣x2+（1﹣k）x+1，‎ h（x）的对称轴是x=，‎ ‎①当≤1时，即k≥﹣1，‎ 易知h（x）在（1，x0）上递减，‎ ‎∴h（x）＜h（1）=1﹣k，‎ 若k≥1，则h（x）≤0，‎ ‎∴g′（x）≤0，‎ ‎∴g（x）在（1，x0）递减，‎ ‎∴g（x）＜g（1）=0，不适合题意．‎ 若﹣1≤k＜1，则h（1）＞0，‎ ‎∴必存在x0使得x∈（1，x0）时，g′（x）＞0，‎ ‎∴g（x）在（1，x0）递增，‎ ‎∴g（x）＞g（1）=0恒成立，适合题意．‎ ‎②当＞1时，即k＜﹣1，‎ 易知必存在x0使得h（x）在（1，x0）递增，‎ ‎∴h（x）＞h（1）=1﹣k＞0，‎ ‎∴g′（x）＞0，∴g（x）在（1，x0）递增，‎ ‎∴g（x）＞g（1）=0恒成立，适合题意．‎ 综上，k的取值范围是（﹣∞，1）．‎ ‎　‎ ‎22．（10分）在平面直角坐标系xOy中，直线l过点（1，0），倾斜角为α，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程是．‎ ‎（1）写出直线l的参数方程和曲线C的直角坐标方程；‎ ‎（2）若，设直线l与曲线C交于A，B两点，求△AOB的面积．‎ ‎【解答】（1）直线L的参数方程为：（α为参数）．‎ 曲线C的极坐标方程是，‎ 转化为直角坐标方程为：y2=8x ‎（2）当时，直线l的参数方程为：（t为参数），‎ 代入y2=8x得到：．（t1和t2为A和B的参数），‎ 所以：，t1t2=﹣16．‎ 所以：．‎ O到AB的距离为：d=．‎ 则：=．‎ ‎　‎ ‎23．设函数f（x）=|x+3|，g（x）=|2x﹣1|．‎ ‎（1）解不等式f（x）＜g（x）；‎ ‎（2）若2f（x）+g（x）＞ax+4对任意的实数x恒成立，求a的取值范围．‎ ‎【解答】解：（1）由已知得|x+3|＜|2x﹣1|，‎ 即|x+3|2＜|2x﹣1|2，‎ 则有3x2﹣10x﹣8＞0，‎ ‎∴x＜﹣或x＞4，‎ 故不等式的解集是（﹣∞，﹣）∪（4，+∞）；‎ ‎（2）由已知，设h（x）=2f（x）+g（x）=2|x+3|+|2x﹣1|‎ ‎=，‎ 当x≤﹣3时，只需﹣4x﹣5＞ax+4恒成立，‎ 即ax＜﹣4x﹣9，‎ ‎∵x≤﹣3＜0，‎ ‎∴a＞=﹣4﹣恒成立，‎ ‎∴a＞，∴a＞﹣1，‎ 当﹣3＜x＜时，只需7＞ax+4恒成立，‎ 即ax﹣3＜0恒成立，‎ 只需，‎ ‎∴，‎ ‎∴﹣1≤a≤6，‎ 当x≥时，只需4x+5＞ax+4恒成立，‎ 即ax＜4x+1，‎ ‎∵x≥＞0，∴a＜=4+恒成立，‎ ‎∵4+＞4，且无限趋近于4，‎ ‎∴a≤4，‎ 综上，a的取值范围是（﹣1，4]．‎ ‎　‎