2018年广东省佛山市顺德区高考数学一模试卷（理科） 22页

‎2018年广东省佛山市顺德区高考数学一模试卷（理科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1．（5分）已知集合A={x|﹣1≤x≤3}，B={x∈Z|x2＜5}，则A∩B=（　　）‎ A．{0，1} B．{﹣1，0，1，2} C．{﹣1，0，1} D．{﹣2，﹣1，0，1，2}‎ ‎2．（5分）已知复数z=1﹣i，则下列命题中正确的个数为：（　　）‎ ‎①|z|=；②=1+i；③z的虚部为﹣i．‎ A．0 B．1 C．2 D．3‎ ‎3．（5分）向量=（1，x+1），=（1﹣x，2），⊥，则（+）（﹣）=（　　）‎ A．﹣15 B．15 C．﹣20 D．20‎ ‎4．（5分）△ABC中，tanA=，AC=2，BC=4，则AB=（　　）‎ A．2﹣ B．﹣ C．+ D．2+‎ ‎5．（5分）将一根长为6m的绳子剪为二段，则其中一段大于另一段2倍的概率为（　　）‎ A． B． C． D．‎ ‎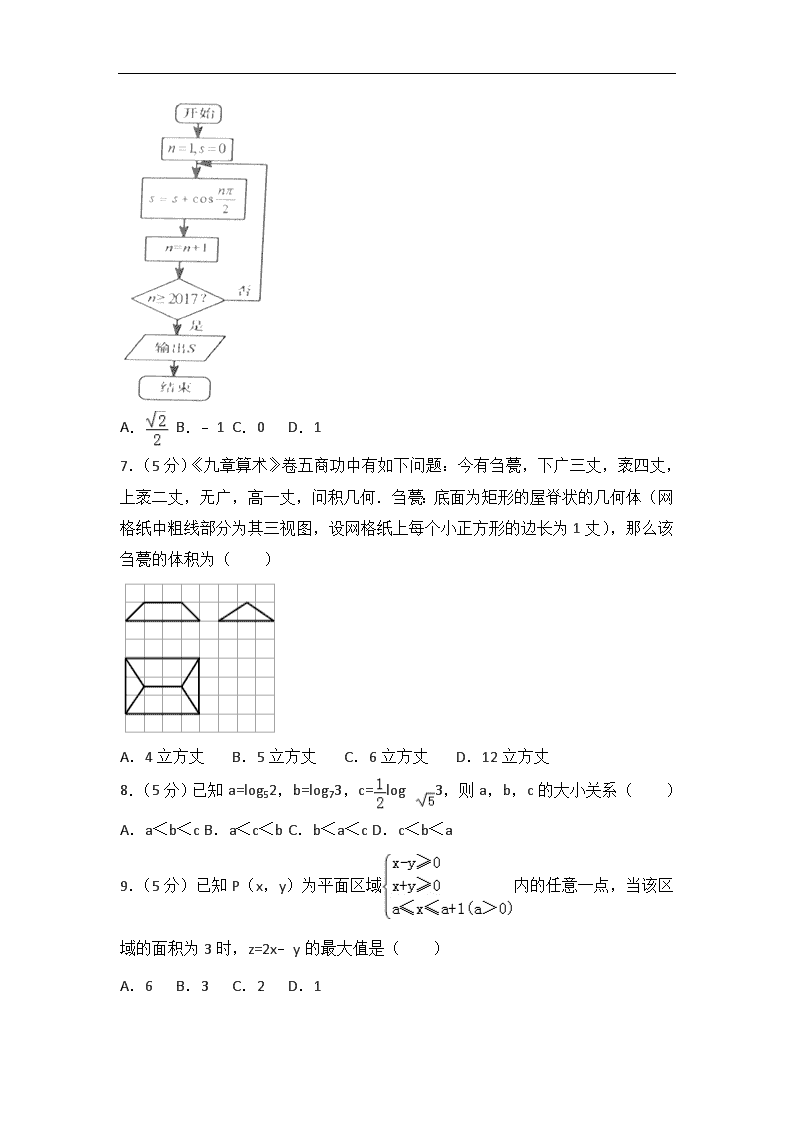6．（5分）执行如图所示的程序框图，输出的S值是（　　）‎ A． B．﹣1 C．0 D．1‎ ‎7．（5分）《九章算术》卷五商功中有如下问题：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何．刍甍：底面为矩形的屋脊状的几何体（网格纸中粗线部分为其三视图，设网格纸上每个小正方形的边长为1丈），那么该刍甍的体积为（　　）‎ A．4立方丈 B．5立方丈 C．6立方丈 D．12立方丈 ‎8．（5分）已知a=log52，b=log73，c=log3，则a，b，c的大小关系（　　）‎ A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜b＜a ‎9．（5分）已知P（x，y）为平面区域内的任意一点，当该区域的面积为3时，z=2x﹣y的最大值是（　　）‎ A．6 B．3 C．2 D．1‎ ‎10．（5分）已知三棱锥S﹣ABC的各顶点都在一个半径为r的球面上，且SA=SB=SC=1，AB=BC=AC=，则球的表面积为（　　）‎ A．4π B．3π C．8π D．12π ‎11．（5分）若圆（x﹣）2+（y﹣1）2=9与双曲线﹣=1（a＞0，b＞0）经过二、四象限的渐近线，交于A，B两点且|AB|=2，则此双曲线的离心率为（　　）‎ A． B． C．2 D．‎ ‎12．（5分）对于实数a、b，定义运算“⊗”：a⊗b=，设f（x）=（2x﹣3）⊗（x﹣3），且关于x的方程f（x）=k（k∈R）恰有三个互不相同的实根x1、x2、x3，则x1•x2•x3取值范围为（　　）‎ A．（0，3） B．（﹣1，0） C．（﹣∞，0） D．（﹣3，0）‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分）.‎ ‎13．（5分）若sin（α+β）cosα﹣cos（α+β）sinα=，则cos2β=　 　．‎ ‎14．（5分）4名同学去参加3 个不同的社团组织，每名同学只能参加其中一个社团组织，且甲乙两位同学不参加同一个社会团体，则共有　 　种结果．‎ ‎15．（5分）已知f（x）=f（4﹣x），当x≤2时，f（x）=ex，f′（3）+f（3）=　 　．‎ ‎16．（5分）设抛物线y2=4x的焦点为F，准线为l，过焦点的直线交抛物线于A，B两点，分别过A，B作l的垂线，垂足为C，D，若|AF|=2|BF|，则三角形CDF的面积为　 　．‎ ‎　‎ 三、解答题：本大题共5小题，共70分．解答写出文字说明、证明过程或演算过程．‎ ‎17．（12分）已知数列{an}的前n项和为Sn，an＞0且满足an=2Sn﹣﹣（n∈‎ N*）．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）求数列{}的前n项和Tn．‎ ‎18．（12分）如图，在三棱锥D﹣ABC中，DA=DB=DC，E为AC上的一点，DE⊥平面ABC，F为AB的中点．‎ ‎（Ⅰ）求证：平面ABD⊥平面DEF；‎ ‎（Ⅱ）若AD⊥DC，AC=4，∠BAC=45°，求二面角A﹣BD﹣C的余弦值．‎ ‎19．（12分）某市市民用水拟实行阶梯水价，每人用水量不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费，从该市随机调查了100位市民，获得了他们某月的用水量数据，整理得到如下频率分布直方图，并且前四组频数成等差数列，‎ ‎（Ⅰ）求a，b，c的值及居民用水量介于2﹣2.5的频数；‎ ‎（Ⅱ）根据此次调查，为使80%以上居民月用水价格为4元/立方米，应定为多少立方米？（精确到小数掉后2位）‎ ‎（Ⅲ）若将频率视为概率，现从该市随机调查3名居民的用水量，将月用水量不超过2.5立方米的人数记为X，求其分布列及其均值．‎ ‎20．（12分）已知椭圆C的中心在原点，焦点在x轴上，离心率等于，它的一个顶点恰好是抛物线x2=﹣4y的焦点．‎ ‎（Ⅰ）求椭圆C的标准方程；‎ ‎（Ⅱ）若圆O：x2+y2=r2与椭圆C交于A，B，C，D四点，当半径r为多少时，四边形ABCD的面积最大？并求出最大面积．‎ ‎21．（12分）设函数f（x）=xlnx﹣ax+1，g（x）=﹣2x3+3x2﹣x+．‎ ‎（Ⅰ）求函数f（x）在[，e]上有两个零点，求a的取值范围；‎ ‎（Ⅱ）求证：f（x）+ax＞g（x）．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎22．（10分）在直角坐标系xOy中，曲线C1的参数方程为（α为参数），曲线C1经过坐标变换后得到的轨迹为曲线C2．‎ ‎（Ⅰ）求C2的极坐标方程；‎ ‎（Ⅱ）在以O为极点，x轴的正半轴为极轴的极坐标中，射线θ=与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知函数f（x）=|x﹣3|﹣|x+5|．‎ ‎（Ⅰ）求不等式f（x）≤2的解集；‎ ‎（Ⅱ）设函数f（x）的最大值为M，若不等式x2+2x+m≥M恒成立，求m的取值范围．‎ ‎　‎ ‎2018年广东省佛山市顺德区高考数学一模试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1．（5分）已知集合A={x|﹣1≤x≤3}，B={x∈Z|x2＜5}，则A∩B=（　　）‎ A．{0，1} B．{﹣1，0，1，2} C．{﹣1，0，1} D．{﹣2，﹣1，0，1，2}‎ ‎【解答】解：∵A={x|﹣1≤x≤3}，B={x∈Z|x2＜5}={x∈Z|﹣＜x＜}={﹣2，﹣1，0，1，2}，‎ ‎∴A∩B={﹣1，0，1，2}，‎ 故选：B．‎ ‎　‎ ‎2．（5分）已知复数z=1﹣i，则下列命题中正确的个数为：（　　）‎ ‎①|z|=；②=1+i；③z的虚部为﹣i．‎ A．0 B．1 C．2 D．3‎ ‎【解答】解：∵z=1﹣i，‎ ‎∴|z|=，故①正确；‎ ‎，故②正确；‎ z的虚部为﹣1，故③错误．‎ ‎∴正确命题的个数为2个．‎ 故选：C．‎ ‎　‎ ‎3．（5分）向量=（1，x+1），=（1﹣x，2），⊥，则（+）（﹣）=（　　）‎ A．﹣15 B．15 C．﹣20 D．20‎ ‎【解答】解：向量=（1，x+1），=（1﹣x，2），‎ 若⊥，则•=（1﹣x）+2（x+1）=x+3=0，‎ 解可得x=﹣3，‎ 则=（1，﹣2），=（4，2），‎ ‎（+）=（5，0），（﹣）=（﹣3，﹣4）；　‎ 则（+）（﹣）=﹣15；‎ 故选：A．‎ ‎　‎ ‎4．（5分）△ABC中，tanA=，AC=2，BC=4，则AB=（　　）‎ A．2﹣ B．﹣ C．+ D．2+‎ ‎【解答】解：已知tanA=，‎ 由于：0＜A＜π，‎ 解得：A=，‎ 利用余弦定理：BC2=AC2+AB2﹣2AC•AB•cosA，‎ 解得：AB=（负值舍去）．‎ 故选：C．‎ ‎　‎ ‎5．（5分）将一根长为6m的绳子剪为二段，则其中一段大于另一段2倍的概率为（　　）‎ A． B． C． D．‎ ‎【解答】解：绳子的长度为6m，折成两段后，设其中一段长度为x，则另一段长度6﹣x，‎ 记“其中一段长度大于另一段长度2倍”为事件A，‎ 则A={x|}={x|0＜x＜2或4＜x≤6}，‎ ‎∴P（A）=，‎ 故选：B．‎ ‎　‎ ‎6．（5分）执行如图所示的程序框图，输出的S值是（　　）‎ A． B．﹣1 C．0 D．1‎ ‎【解答】解：本题为直到型循环结构的程序框图，由框图的流程知：‎ 算法的功能是求S=cos+cosπ+…+cos的值，‎ ‎∵y=cos的周期为4，2017=504×4+1‎ ‎∴输出S=504×（cos+cosπ+cos+cos2π）+cos=0 ‎ 故选：C ‎　‎ ‎7．（5分）《九章算术》卷五商功中有如下问题：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何．刍甍：底面为矩形的屋脊状的几何体（网格纸中粗线部分为其三视图，设网格纸上每个小正方形的边长为1丈），那么该刍甍的体积为（　　）‎ A．4立方丈 B．5立方丈 C．6立方丈 D．12立方丈 ‎【解答】解：三棱柱的底面是边长为3，高为1的等腰三角形．三棱柱的高为2．‎ ‎∴三棱柱的体积V=．‎ 两个相同的四棱锥合拼，可得底面边长为2和3的矩形的四棱锥，其高为1．‎ ‎∴体积V==2．‎ 该刍甍的体积为：3+2=5．‎ 故选：B．‎ ‎　‎ ‎8．（5分）已知a=log52，b=log73，c=log3，则a，b，c的大小关系（　　）‎ A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜b＜a ‎【解答】解：∵c=log3=log53＞log73，‎ b=log73＞=，a=log52＜=，‎ 则a，b，c的大小关系为：a＜b＜c．‎ 故选：A．‎ ‎　‎ ‎9．（5分）已知P（x，y）为平面区域 内的任意一点，当该区域的面积为3时，z=2x﹣y的最大值是（　　）‎ A．6 B．3 C．2 D．1‎ ‎【解答】解：由作出可行域如图，‎ 由图可得A（a，a），D（a，a），B（a+1，a+1），C（a+1，﹣a﹣1）‎ 由该区域的面积为3时，×1=3，得a=1．‎ ‎∴A（1，1），C（2，﹣2）‎ 化目标函数z=2x﹣y为y=2x﹣z，‎ ‎∴当y=2x﹣z过C点时，z最大，等于2×2﹣（﹣2）=6．‎ 故选：A．‎ ‎　‎ ‎10．（5分）已知三棱锥S﹣ABC的各顶点都在一个半径为r的球面上，且SA=SB=SC=1，AB=BC=AC=，则球的表面积为（　　）‎ A．4π B．3π C．8π D．12π ‎【解答】解：三棱锥S﹣ABC中，SA=SB=SC=1，AB=BC=AC=，‎ ‎∴共顶点S的三条棱两两相互垂直，且其长均为1，‎ 三棱锥的四个顶点同在一个球面上，三棱锥是正方体的一个角，扩展为正方体，‎ 三棱锥的外接球与正方体的外接球相同，正方体的对角线就是球的直径，‎ 所以球的直径为：，半径为，‎ 外接球的表面积为：4π×（）2=3π．‎ 故选：B．‎ ‎　‎ ‎11．（5分）若圆（x﹣）2+（y﹣1）2=9与双曲线﹣=1（a＞0，b＞0）经过二、四象限的渐近线，交于A，B两点且|AB|=2，则此双曲线的离心率为（　　）‎ A． B． C．2 D．‎ ‎【解答】解：依题意可知双曲线的经过二、四象限的渐近线方程为bx+ay=0，‎ ‎∵|AB|=2，圆的圆心为（，1），半径为3，‎ ‎∴圆心到渐近线的距离为=，‎ 即=，‎ 解得b=a，‎ ‎∴c==a，‎ ‎∴双曲线的离心率为e==．‎ 故选：A．‎ ‎　‎ ‎12．（5分）对于实数a、b，定义运算“⊗”：a⊗b=，设f（x）=（2x﹣3）⊗（x﹣3），且关于x的方程f（x）=k（k∈R）恰有三个互不相同的实根x1、x2、x3，则x1•x2•x3取值范围为（　　）‎ A．（0，3） B．（﹣1，0） C．（﹣∞，0） D．（﹣3，0）‎ ‎【解答】解：∵a⊗b=，‎ ‎∴f（x）=（2x﹣3）⊗（x﹣3）=，‎ 其图象如下图所示：‎ 由图可得：x1=﹣k，x2•x3=k，‎ 故x1•x2•x3=﹣k2，k∈（0，3），‎ ‎∴x1•x2•x3∈（﹣3，0），‎ 故选：D．‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分）.‎ ‎13．（5分）若sin（α+β）cosα﹣cos（α+β）sinα=，则cos2β=　﹣　．‎ ‎【解答】解：∵sin（α+β）cosα﹣cos（α+β）sinα=sin[（α+β）﹣α]=sinβ=，‎ 则cos2β=1﹣2sin2β=1﹣2•=﹣，‎ 故答案为：﹣．‎ ‎　‎ ‎14．（5分）4名同学去参加3 个不同的社团组织，每名同学只能参加其中一个社团组织，且甲乙两位同学不参加同一个社会团体，则共有　54　种结果．‎ ‎【解答】解：根据题意，先计算4名同学去参加3 个不同的社团组织的情况数目，‎ ‎4个同学中每人可以在3 个不同的社团组织任选1个，即每人有3种不同的选法，‎ 则4人有3×3×3×3=81种情况，‎ 再计算甲乙参加同一个社团组织的情况数目，‎ 若甲乙参加同一个社团组织，甲乙两人有3种情况，‎ 剩下的2人每人有3种不同的选法，则剩下的2人有3×3=9种情况，‎ 则甲乙参加同一个社团组织的情况有3×9=27种；‎ 则甲乙两位同学不参加同一个社团组织的情况有81﹣27=54种；‎ 故答案为：54．‎ ‎　‎ ‎15．（5分）已知f（x）=f（4﹣x），当x≤2时，f（x）=ex，f′（3）+f（3）=　0　．‎ ‎【解答】解：由f（x）=f（4﹣x）可得，‎ 函数f（x）的图象关于直线x=2对称，‎ 当x≤2时，f（x）=ex，f′（x）=ex，‎ ‎∴f（3）=f（1）=e，‎ f′（3）=﹣f′（1）=﹣e，‎ 故f′（3）+f（3）=0，‎ 故答案为：0．‎ ‎　‎ ‎16．（5分）设抛物线y2=4x的焦点为F，准线为l，过焦点的直线交抛物线于A，B两点，分别过A，B作l的垂线，垂足为C，D，若|AF|=2|BF|，则三角形CDF的面积为　3　．‎ ‎【解答】解：如图，抛物线y2=4x的焦点F（1，0），准线l为x=﹣1，‎ 设l所在直线方程为y=k（x﹣1），设A（x1，y1），B（x2，y2）‎ 联立，得k2x2﹣（2k2+4）x+k2=0，‎ ‎∴x1x2=1，①‎ ‎∵|AF|=2|BF|，‎ ‎∴x1+1=2（x2+1），②‎ 由①②解得x2=，x1=2，或x1=﹣1，x2=﹣1（舍去）‎ ‎∴y1=2，y2=﹣，‎ ‎∴|CD|=y1﹣y2=3，‎ ‎∵|FG|=1+1=2，‎ ‎∴S△CDF=×|CD|×|FG|=×3×2=3，‎ 故答案为：3‎ ‎　‎ 三、解答题：本大题共5小题，共70分．解答写出文字说明、证明过程或演算过程．‎ ‎17．（12分）已知数列{an}的前n项和为Sn，an＞0且满足an=2Sn﹣﹣（n∈N*）．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）求数列{}的前n项和Tn．‎ ‎【解答】解：（Ⅰ）当n=1时，，解得a1=1；‎ 由an=2Sn﹣﹣，整理得，①‎ ‎∴，②‎ ‎②﹣①得：，‎ ‎∴（an+1+an）（an+1﹣an﹣2）=0，‎ ‎∵an＞0，‎ ‎∴an+1﹣an﹣2=0，即an﹣1﹣an=2．‎ ‎∴数列{an}是以1为首项，以2为公差的等差数列，‎ 则an=1+2（n﹣1）=2n﹣1；‎ ‎（Ⅱ）=，③‎ ‎，④‎ ‎③﹣④得：‎ ‎==．‎ ‎∴．‎ ‎　‎ ‎18．（12分）如图，在三棱锥D﹣ABC中，DA=DB=DC，E为AC上的一点，DE⊥平面ABC，F为AB的中点．‎ ‎（Ⅰ）求证：平面ABD⊥平面DEF；‎ ‎（Ⅱ）若AD⊥DC，AC=4，∠BAC=45°，求二面角A﹣BD﹣C的余弦值．‎ ‎【解答】证明：（Ⅰ）∵DE⊥平面ABC，∴AB⊥DE，‎ 又∵F为AB的中点，DA=DB，∴AB⊥DF，‎ DF∩DE=E，且DF、DE⊂平面DEF，‎ 又∵AB⊂平面ABD，‎ ‎∴平面ABD⊥平面DEF；‎ 解：（Ⅱ）∵DE⊥平面ABC，∴AC⊥DE，‎ 又∵DA=DC，∴E为AC中点，‎ ‎∵F是AB中点，∴EF∥BC，‎ 由（Ⅰ）知AB⊥EF，∴AB⊥BC，‎ 又∵∠BAC=45°，∴△ABC为等腰直角三角形，AC=4，‎ ‎∴AB=BC=DA=DB=DC=2，‎ 取BD中点G，连结AG、CG，则AG⊥DB，CG⊥DB，‎ ‎∴∠AGC为二面角A﹣BD﹣C的平面角，‎ 在△AGC中，cos∠AGC==﹣，‎ ‎∴二面角A﹣BD﹣C的余弦值为﹣．‎ ‎　‎ ‎19．（12分）某市市民用水拟实行阶梯水价，每人用水量不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费，从该市随机调查了100位市民，获得了他们某月的用水量数据，整理得到如下频率分布直方图，并且前四组频数成等差数列，‎ ‎（Ⅰ）求a，b，c的值及居民用水量介于2﹣2.5的频数；‎ ‎（Ⅱ）根据此次调查，为使80%以上居民月用水价格为4元/立方米，应定为多少立方米？（精确到小数掉后2位）‎ ‎（Ⅲ）若将频率视为概率，现从该市随机调查3名居民的用水量，将月用水量不超过2.5立方米的人数记为X，求其分布列及其均值．‎ ‎【解答】解：（Ⅰ）∵前四组频数成等差数列，∴所对应的频率也成等差数列，‎ 设a=0.2+d，b=0.2+2d，c=0.2+3d，‎ ‎∴0.5（a+0.2+d+0.2+2d+0.2+3d+0.2+d+0.1+0.1+0.1）=1，‎ 解得d=0.1，a=0.3，b=0.4，c=0.5．‎ 居民月用水量介于2～2.5的频率为0.25．‎ 居民月用水量介于2～2.5的频数为0.25×100=25人．‎ ‎（Ⅱ）由图可知，居民月用水量小于2.5的频率为0.7＜0.8，‎ ‎∴为使80%以上居民月用水价格为4元/立方米，‎ 应定为ω=2.5+≈2.83立方米．‎ ‎（Ⅲ）将频率视为概率，设A代表居民月用水量，由图知：‎ P（A≤2.5）=0.7，‎ 由题意X～B（3，0.7），‎ P（X=0）==0.027，‎ P（X=1）==0.189，‎ P（X=2）==0.441，‎ P（X=3）==0.343．‎ ‎∴X的分布列为：‎ ‎ X ‎ 0‎ ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ P ‎ 0.027‎ ‎ 0.189‎ ‎ 0.441‎ ‎ 0.343‎ ‎∵X～B（3，0.7），∴E（X）=np=2.1．‎ ‎　‎ ‎20．（12分）已知椭圆C的中心在原点，焦点在x轴上，离心率等于，它的一个顶点恰好是抛物线x2=﹣4y的焦点．‎ ‎（Ⅰ）求椭圆C的标准方程；‎ ‎（Ⅱ）若圆O：x2+y2=r2与椭圆C交于A，B，C，D四点，当半径r为多少时，四边形ABCD的面积最大？并求出最大面积．‎ ‎【解答】解：（Ⅰ）∵椭圆C的中心在原点，焦点在x轴上，‎ 它的一个顶点恰好是抛物线x2=﹣4y的焦点，离心率等于，‎ ‎∴设椭圆方程为，‎ 根据题意得：，‎ 解得：‎ 所以椭圆C的方程为；‎ ‎（Ⅱ）设A（x0，y0），则矩形ABCD的面积S=4|x0y0|‎ 由，得，‎ ‎∴==﹣（﹣2）2+1，‎ ‎∴时，（）max=1，‎ ‎∴Smax=4×1=4，‎ 此时r2==．‎ 即r=．‎ ‎　‎ ‎21．（12分）设函数f（x）=xlnx﹣ax+1，g（x）=﹣2x3+3x2﹣x+．‎ ‎（Ⅰ）求函数f（x）在[，e]上有两个零点，求a的取值范围；‎ ‎（Ⅱ）求证：f（x）+ax＞g（x）．‎ ‎【解答】解：（Ⅰ）由f（x）=xlnx﹣ax+1=0，得：a=lnx+，‎ 问题转化为a=lnx+在[，e]上有2个不同的解，‎ 令h（x）=lnx+，x∈[，e]，则h′（x）=，‎ 令h′（x）＞0，解得：x＞1，令h′（x）＜0，解得：0＜x＜1，‎ 故h（x）在（0，1）递减，在（1，+∞）递增，‎ 而h（1）=1，h（）=e﹣1，h（e）=1+＜e﹣1，‎ 故a的范围是（1，1+）；‎ ‎（Ⅱ）要证f（x）+ax≥g（x），只要证明xlnx+1≥g（x），‎ 先证xlnx+1≥x，构造函数F（x）=xlnx+1﹣x，‎ ‎∵F′（x）=1+lnx﹣1=lnx，‎ x=1时，F′（x）=0，当0＜x＜1时，F′（x）＜0，x＞1时，F′（x）＞0，‎ 故F（x）在[0，1]递减，在[1，+∞）递增，‎ 故F（x）≥F（1）=0，即证xlnx+1≥x，等号成立当且仅当x=1，‎ 再证明x∈[，+∞）时，g（x）≤x，‎ 构造函数G（x）=x﹣g（x）=2，‎ ‎∵G′（x）=6≥0，‎ ‎∴G（x）在[，+∞）递增，‎ ‎∴G（x）≥G（）=0，即证明g（x）≤x，等号成立当且仅当x=，‎ 故x∈（0，）时，构造函数φ（x）=f（x）+ax=xlnx+1，‎ ‎∵φ′（x）=1+lnx，∴x=时，φ′（x）=0，当0＜x＜时，φ′（x）＜0，‎ 当＜x＜时，φ′（x）＞0，‎ 即φ（x）在（0，）递减，在（，）递增，‎ ‎∴x∈（0，）时，φ（x）≥φ（）=1﹣，‎ ‎∵g′（x）=﹣6+1，‎ x∈（0，）时，﹣＜g′（x）＜1，‎ 又g′（0）=﹣＜0，g′（）=1＞0，‎ 存在x0∈（0，），使得g′（x0）=0，且g（x）在（0，x0）递减，在（x0，）递增，‎ 故x∈（0，）时，g（x）＜max{g（0），g（）}=，‎ ‎∴g（x）＜＜1﹣≤φ（x），‎ 综上，对任意x＞0，f（x）+ax＞g（x）．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎22．（10分）在直角坐标系xOy中，曲线C1的参数方程为（α为参数），曲线C1经过坐标变换后得到的轨迹为曲线C2．‎ ‎（Ⅰ）求C2的极坐标方程；‎ ‎（Ⅱ）在以O为极点，x轴的正半轴为极轴的极坐标中，射线θ=与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|．‎ ‎【解答】解：（Ⅰ）曲线C1的参数方程为（α为参数），‎ 转化为直角坐标方程为：x2+y2=1，‎ 曲线C1经过坐标变换后得到的轨迹为曲线C2．‎ 即：，‎ 故C2的直角坐标方程为：．‎ 转化为极坐标方程为：．‎ ‎（Ⅱ）曲线C1的参数方程为（α为参数），转化为极坐标方程为ρ1=1，‎ 由题意得到：A（1，），‎ 将B（ρ，）代入坐标方程：．‎ 得到，‎ 则：|AB|=．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知函数f（x）=|x﹣3|﹣|x+5|．‎ ‎（Ⅰ）求不等式f（x）≤2的解集；‎ ‎（Ⅱ）设函数f（x）的最大值为M，若不等式x2+2x+m≥M恒成立，求m的取值范围．‎ ‎【解答】解：（Ⅰ）x≥3时，f（x）=﹣8，此时f（x）≤2恒成立，‎ ‎﹣5＜x＜3时，f（x）=﹣2x﹣2，‎ 由f（x）≤2，解得：﹣2≤x＜3，‎ x≤﹣5时，f（x）=8，此时f（x）≤2，无解，‎ 综上，f（x）≤2的解集是{x|x≥﹣2}；‎ ‎（Ⅱ）由（Ⅰ）得f（x）=，‎ 易知函数的最大值是8，‎ 若x2+2x+m≥8恒成立，‎ 得m≥﹣x2﹣2x+8恒成立，‎ 即m≥﹣（x+1）2+9，‎ 故m≥9．‎ ‎　‎