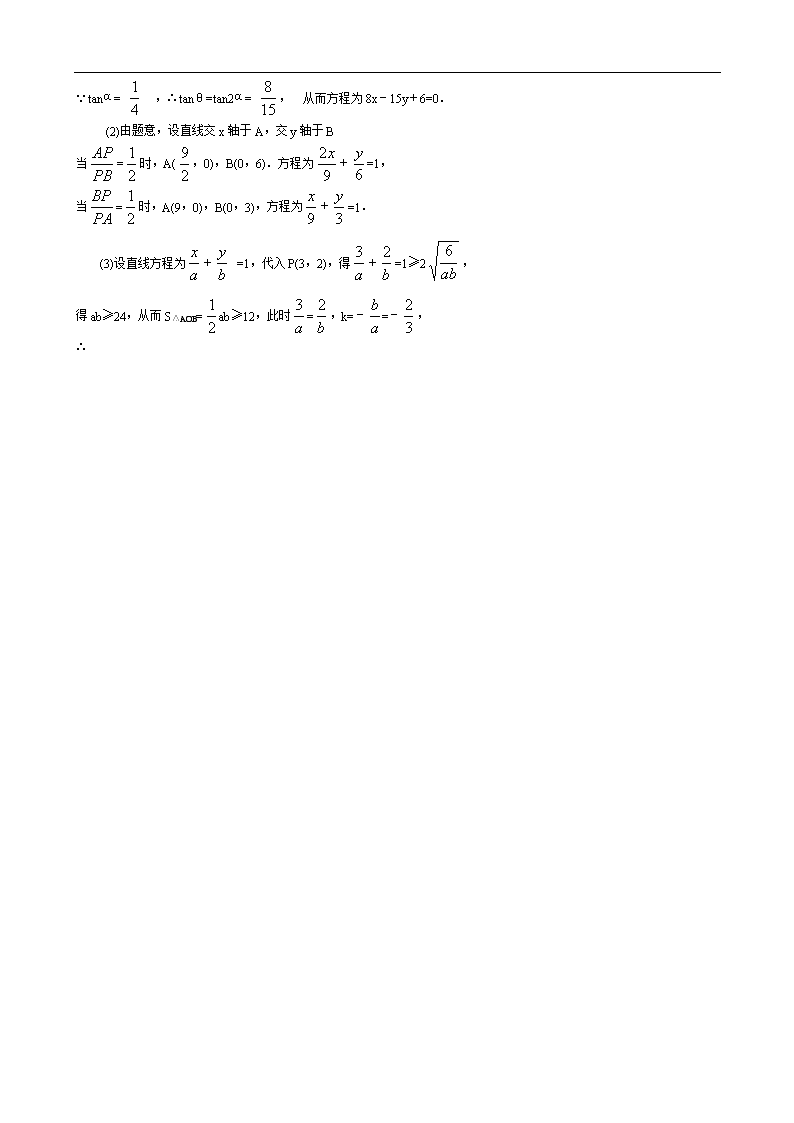高中数学必修2教案：直线的两点式方程 3页

课时46直线的两点式方程 一、选择题 ‎1、如果AC<0, 且BC<0,那么直线不通过 （ ）‎ A. 第一象限 B. 第二象限C. 第三象限 D. 第四象限 ‎2、经过点A（1，2）并且在坐标轴上截距的绝对值相等的直线共有（ ）‎ A. 4条 B. 3条 C. 2条 D.1条 ‎3、的一个顶点是A（3，1），∠B、∠C的平分线分别是x=0、x=y，则直线AB 的方程为（ ）‎ A. B. ‎ C. D. ‎ ‎4、设Ａ、Ｂ是x轴上的两点，点Ｐ的横坐标为２，且|ＰＡ|＝|ＰＢ|，若直线ＰＡ的方程为x－y＋1=0，则直线ＰＢ的方程是（　　　）‎ A．x＋y－5=0 B．2x－y－1=0 ‎ ‎ C．x－2y＋4=0 D．2x＋y－7=0‎ ‎5、下列命题中正确的是( )‎ A. 经过点P0(x0，y0)的直线都可以用方程y－y0=k(x－x0)表示 B. 经过定点A(0，b)的直线都可以用方程y=kx＋b表示．‎ C. 经过任意两个不同点P1(x1，y1)， P2(x2，y2)的直线都可用方程(x2－x1)(y－y1)=(y2－y1)(x－x1)表示． ‎ D. 不经过原点的直线都可以用方程＋=1表示．‎ 二、 填空题 ‎6、直线在两坐标轴上截距之和为2，则实数__________________.‎ ‎7、直线经过连接A（-1，-2）、B（3，4）的线段的中点，则实数__________________.‎ ‎8、直线与垂直，垂足为，则__________________.‎ ‎9、直线与两坐标轴围成的面积是__________________.‎ ‎10、已知三点A（2，-1）、B（5，7）、C（-1，-3），则通过的重心G及顶点A和原点连线的中点M的直线方程是__________________.‎ 三、解答题 ‎11、已知正方形边长为4，其中心在原点，对角线在坐标轴上，求正方形各边所在的直线的方程。‎ ‎12、在直角坐标系中，三个顶点A（0，3）、B（3，3）、C（2，0），若直线将分割成面积相等的两部分，求实数的值。‎ ‎13、一条光线从点A（3，2）发出，经 轴反射，通过点B（-1，6），求入射光线和反射光线所在的直线方程。‎ ‎14、已知中A（-8，2），AB边上中线CE所在的直线方程为，AC边上中线BD所在的直线方程为，求直线BC的方程。‎ ‎15、一条直线经过P（3，2），并且分别满足下列条件，求直线方程．‎ ‎(1)倾斜角是直线x－4y＋3=0的倾斜角的2倍；‎ ‎(2)夹在两坐标轴间的线段被P分成1：2．‎ ‎(3)与x轴，y轴正半轴交于A、B两点，且△AOB的面积最小．‎ 课时46直线的两点式方程 ‎1、C 2、B 3、D 4、A 5、C 6、-24 7、2 8、-4 9、 10、‎ ‎11、解：利用截距式可得 ，，，，。‎ ‎12、解：，直线与AC的交点D，与AB的交点E,,解得.‎ ‎13、解：点A（3，2）关于轴的对称点，由两点式的直线的方程为，同理直线的方程为，入射光线的方程为，反射光线的方程为。‎ ‎14、解：设，则AB的中点E的坐标为，由题意得：，解得，同理得C（5，0），故直线BC为 ‎15、解 （1）设所求直线倾斜角为θ，已知直线的倾斜角为α，则θ=2α ‎ ‎∵tanα= ，∴tanθ=tan2α= ， 从而方程为8x－15y＋6=0．‎ ‎ (2)由题意，设直线交x轴于A，交y轴于B 当=时，A(，0)，B(0，6)．方程为＋=1，‎ 当=时，A(9，0)，B(0，3)，方程为＋=1．‎ ‎(3)设直线方程为＋ =1，代入P(3，2)，得＋=1≥2，‎ 得ab≥24，从而S△AOB=ab≥12，此时=，k=－=－，‎ ‎∴‎