江西省四校联盟2020届高三第一次联考数学（文）试题 Word版含解析 26页

www.ks5u.com ‎2020届四校联盟高三第一次联考试卷 文科数学 一、选择题（本题12小题，每小题5分，此60分）‎ ‎1.已知集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 化简集合，按交集定义，即可求解.‎ ‎【详解】由，得，所以，‎ 故选：B．‎ ‎【点睛】本题考查集合间的运算，属于基础题.‎ ‎2.已知是虚数单位，若，则的共轭复数对应的点在复平面的(　　)‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 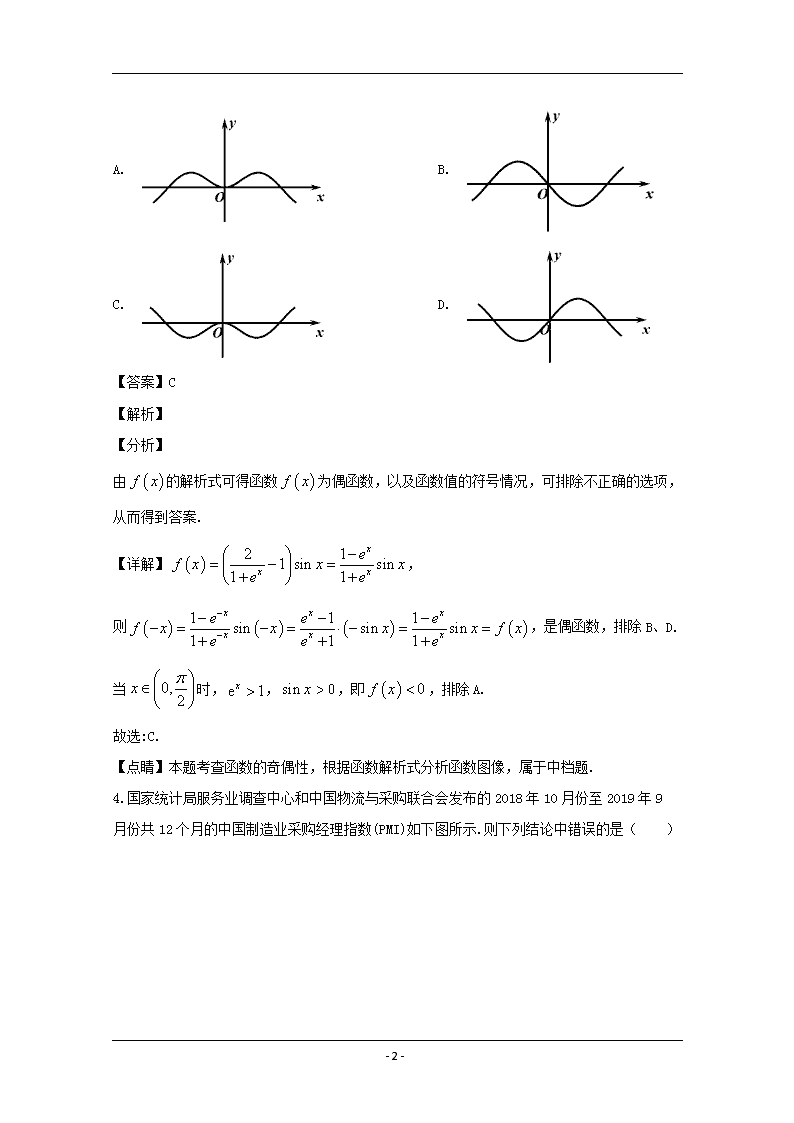第四象限 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 把已知等式变形，再由复数代数形式的乘除运算化简，求出z的坐标得答案．‎ ‎【详解】解：由2+i＝z（1﹣i），得z，‎ ‎∴，‎ 则z的共轭复数z对应的点的坐标为（），在复平面的第四象限．‎ 故选D．‎ ‎【点睛】本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．‎ ‎3.函数图象的大致形状是（ ）‎ - 26 -‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由的解析式可得函数为偶函数，以及函数值的符号情况，可排除不正确的选项，从而得到答案.‎ ‎【详解】，‎ 则，是偶函数，排除B、D.‎ 当时，，，即，排除A.‎ 故选:C.‎ ‎【点睛】本题考查函数的奇偶性，根据函数解析式分析函数图像，属于中档题.‎ ‎4.国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是（ ）‎ - 26 -‎ A. 12个月的PMI值不低于50%的频率为 B. 12个月的PMI值的平均值低于50%‎ C. 12个月的PMI值的众数为49.4%‎ D. 12个月的PMI值的中位数为50.3%‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据图形中的信息，可得频率、平均值的估计、众数、中位数，从而得到答案.‎ ‎【详解】对A，从图中数据变化看，PMI值不低于50%的月份有4个，所以12个月的PMI值不低于50%的频率为，故A正确；‎ 对B，由图可以看出，PMI值的平均值低于50%，故B正确；‎ 对C，12个月的PMI值的众数为49.4%，故C正确，；‎ 对D，12个月的PMI值的中位数为49.6%，故D错误 故选：D.‎ ‎【点睛】本题考查频率、平均值的估计、众数、中位数计算，考查数据处理能力，属于基础题.‎ ‎5.射线测厚技术原理公式为，其中分别为射线穿过被测物前后的强度，是自然对数的底数，为被测物厚度，为被测物的密度，是被测物对射线的吸收系数.工业上通常用镅241（）低能射线测量钢板的厚度.若这种射线对钢板的半价层厚度为0.8，钢的密度为7.6，则这种射线的吸收系数为（ ）‎ ‎（注：半价层厚度是指将已知射线强度减弱为一半的某种物质厚度，，结果精确到0.001）‎ - 26 -‎ A. 0.110 B. 0.112 C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据题意知,，代入公式,求出即可.‎ ‎【详解】由题意可得,因为,‎ 所以,即.‎ 所以这种射线的吸收系数为.‎ 故选:C ‎【点睛】本题主要考查知识的迁移能力,把数学知识与物理知识相融合;重点考查指数型函数,利用指数的相关性质来研究指数型函数的性质,以及解指数型方程；属于中档题.‎ ‎6.已知向量满足，点在内，且，设，若，则（ ）‎ A. B. 4 C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据题意由得，建立如图所示的直角坐标系，由，不妨设 ‎，，则，再利用正切的定义结合建立关于的等式，即可解出的值。‎ - 26 -‎ 详解】‎ 由得，建立如图所示的直角坐标系，‎ ‎，不妨设，， ‎ 由得 ‎，‎ ‎ ‎ 故选：C ‎【点睛】本题主要考查了平面向量的坐标表示以及平面向量的坐标运算，属于基础题。‎ ‎7.齐王有上等、中等、下等马各一匹，田忌也有上等、中等、下等马各一匹．田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马．现在从双方的马匹中随机各选一匹进行一场比赛，若有优势的马一定获胜，则齐王的马获胜得概率为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 现从双方的马匹中随机各选一匹进行一场比赛 ,利用列举法求出基本事件有9种，齐王的马获胜包含的基本事件有6种，利用古典概型概率公式可求出齐王的马获胜的概率.‎ ‎【详解】设齐王上等、中等、下等马分別为，田忌上等、中等、下等马分别为，‎ - 26 -‎ 现从双方的马匹中随机各选一匹进行一场比赛,‎ 基本事件有：，共9种，有优势的马一定获胜，齐王的马获胜包含的基本事件有：，共 6种,‎ 齐王的马获胜的概率为，故选C.‎ ‎【点睛】本题主要考查古典概型概率公式的应用，属于中档题，利用古典概型概率公式求概率时，找准基本事件个数是解题的关键，基本亊件的探求方法有 (1)枚举法：适合给定的基本事件个数较少且易一一列举出的；(2)树状图法：适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时，一定要按顺序逐个写出：先，…. ，再，…..依次….… 这样才能避免多写、漏写现象的发生.‎ ‎8.直线分别与轴，轴交于，两点，点在圆上，则面积取值范围是 A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 分析：先求出A，B两点坐标得到再计算圆心到直线距离，得到点P到直线距离范围，由面积公式计算即可 详解：直线分别与轴，轴交于，两点 ‎,则 点P在圆上 圆心为（2，0），则圆心到直线距离 故点P到直线的距离的范围为 - 26 -‎ 则 故答案选A.‎ 点睛：本题主要考查直线与圆，考查了点到直线的距离公式，三角形的面积公式，属于中档题．‎ ‎9.已知三棱柱的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 设的中点为，连接、、，易知即为异面直线与所成的角（或其补角）．由余弦定理，计算得即可．‎ ‎【详解】如图，设的中点为，连接、、，‎ 易知即为异面直线与所成的角（或其补角）‎ 设三棱柱的侧棱与底面边长均为1，‎ 则，，，‎ 由余弦定理，得 故应选B.‎ - 26 -‎ ‎【点睛】本题主要考查了异面直线所成角的求解，通过平移找到所成角是解这类问题的关键，若平移不好作，可采用建系，利用空间向量的运算求解，属于基础题.解答本题时，易知即为异面直线与所成的角（或其补角），进而通过计算的各边长，利用余弦定理求解即可．‎ ‎10.已知函数，给出下列四个命题：‎ ‎①的最小正周期为 ‎②的图象关于直线对称 ‎③在区间上单调递增 ‎④的值域为 ‎⑤在区间上有6个零点 其中所有正确的编号是（ ）‎ A. ②④ B. ①④⑤ C. ③④ D. ②③⑤‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 化简函数，通过，判断①；通过，判断的图象不关于直线对称，判断②；在区间，上，，化简函数的解析式，判断单调性单调递增，判断③；当时，推出，求出最值，当时，求出最值判断④；当时，，在区间，上有无数个零点，判断⑤．‎ - 26 -‎ ‎【详解】‎ 函数，，‎ ‎∴，故函数的最小正周期不是，故①错误.‎ 由于，，∴，故的图象不关于直线对称，故排除②.‎ 在区间上，，，单调递增，故③正确.‎ 当时，，‎ 故它的最大值为2，最小值为；当时，‎ ‎，‎ 综合可得，函数的最大值为2，最小值为，故④正确.‎ 当时，，在区间上有无数个零点，故⑤错误.‎ 故选：C.‎ ‎【点睛】本题考查三角函数的化简求值、函数的单调性以及函数的对称性，考查函数的最值，考查分析问题解决问题的能力，是中档题．‎ ‎11.在锐角中，内角的对边分别为，已知，，则的面积取得最小值时有（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ - 26 -‎ 先由条件、正弦定理及面积公式得出，然后利用基本不等式求出最值及取得最值时的值，然后再用余弦定理算出 ‎【详解】由已知有，‎ 根据正弦定理得，‎ 又，即，‎ 由于，即有，‎ 即有，‎ 由于，即，解得，‎ 当且仅当时取等号，‎ 当，，取最小值，‎ 又（为锐角），则，‎ 则.‎ 故选：D ‎【点睛】本题考查的是正余弦定理、三角形的面积公式及基本不等式，属于综合题.‎ ‎12.已知椭圆的左、右焦点分别为，点，在椭圆上，其中，，若，，则椭圆的离心率的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ - 26 -‎ 先分析得到四边形为矩形，，再由得，由得，化简不等式即得离心率的取值范围.‎ ‎【详解】设，由知，‎ 由在椭圆上，可知四边形矩形，；‎ 由，可得，‎ 由椭圆的定义可得，平方相减可得，‎ ‎∴，而，‎ 即，‎ 由可得，‎ 由，可得，‎ ‎∴，∴，‎ 故选：C.‎ ‎【点睛】本题主要考查椭圆的标准方程及其几何性质，考查椭圆的离心率的计算和基本不等式的应用，意在考查学生对这些知识的理解掌握水平.‎ 二、填空题（本题4小题，每小题5分，共20分）‎ ‎13.函数的图像在点处的切线垂直于直线，则_______.‎ ‎【答案】‎ - 26 -‎ ‎【解析】‎ ‎【分析】‎ 先求出，再解方程即得解.‎ ‎【详解】因为.所以.‎ 因为.‎ 所以.‎ 故答案为：‎ ‎【点睛】本题主要考查求导和导数的几何意义，意在考查学生对这些知识的理解掌握水平.‎ ‎14.若，则___________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用诱导公式，结合二倍角的余弦公式进行求解即可.‎ ‎【详解】因为，所以 ‎.‎ 故答案为：‎ ‎【点睛】本题考查了诱导公式和二倍角的余弦公式的应用，属于基础题.‎ ‎15.已知数列满足，则的最小值为_______.‎ ‎【答案】.‎ ‎【解析】‎ ‎【分析】‎ 根据递推公式和累加法可求得数列的通项公式.代入中,由数列中的性质,结合数列的单调性即可求得最小值.‎ - 26 -‎ ‎【详解】因为,所以,‎ 从而 ‎…,‎ ‎,‎ 累加可得,‎ 而 所以,‎ 则,‎ 因为在递减,在递增 当时,,‎ 当时,,‎ 所以时取得最小值,最小值为.‎ 故答案为:‎ ‎【点睛】本题考查了利用递推公式及累加法求数列通项公式的方法,数列单调性及自变量取值的特征,属于中档题.‎ ‎16.在四棱锥中，底面为正方形，平面平面，且为等边三角形，若四棱锥的体积与四棱锥外接球的表面积大小之比为，则正方形的边长为______.‎ ‎【答案】2‎ ‎【解析】‎ ‎【分析】‎ - 26 -‎ 设正方形的边长为,再根据四棱锥外接一个直三棱柱且外接球相同,进而计算可得外接球的表面积关于的表达式,进而根据四棱锥的体积与四棱锥外接球的表面积大小之比为求得边长即可.‎ ‎【详解】由题,画出图像,取中点.设正方形的边长为,则因为为等边三角形.故.且.‎ 又平面平面且平面平面.‎ 故平面.故四棱锥的体积为.‎ 又四棱锥外接以为底面,为高的直三棱柱,故四棱锥的外接球与该三棱柱外接球相同.则底面的外接圆直径.‎ 故外接球直径,故外接球表面积.故,解得.‎ 即正方形的边长为2‎ 故答案为：2‎ - 26 -‎ ‎【点睛】本题主要考查了锥体外接球的表面积算法,需要根据题意确定四棱锥的外接直三棱柱,根据正弦定理求解底面圆的直径,再利用勾股定理求得外接球的直径关系求解.属于中档题.‎ 三、解答题（共70分，第17-21题为必考题，第22-23题为选考题）‎ ‎（一）必考题：共60分.‎ ‎17.如图，已知四棱锥的底面是菱形，，，为边的中点，点在线段上.‎ ‎（1）证明：平面平面；‎ ‎（2）若，平面，求四棱锥的体积.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）由面面垂直的判定定理可知要证平面平面需证直线与平面垂直，经过观察可知要证平面，进而可转化为证明两条直线与；（2）四棱锥的体积分两部分：一是点到平面的距离：可转化成点到平面的距离，由已知条件可得平面，容易得出的大小；一是的面积：容易知道的面积为的，由此可得棱锥的体积.‎ 试题解析：（1）证明：连接，因为底面是菱形，，‎ 所以是正三角形，‎ 因为为边的中点，，‎ 所以，，，‎ 所以平面，‎ 因为平面，‎ 所以平面平面．‎ - 26 -‎ ‎（2）连接，交于点，连接，‎ 因为∥平面，所以∥，‎ 易知点为的重心，所以，‎ 故，‎ 因为，， 所以，，因为，‎ 所以，即，且，所以平面，‎ 由知，故点到平面的距离为，‎ 因为，‎ 所以四棱锥的体积为．‎ 考点：面面垂直的判定定理、线面垂直的判定定理.‎ ‎18.已知数列的各项均为正数，对任意的，它的前n项和满足，并且成等比数列.‎ ‎（1）求数列的通项公式；‎ ‎（2）设，为数列的前n项和，求.‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据已知等式再写出一个关于的等式，两式作差得到的通项公式，并根据已知条件对通项公式进行取舍；‎ - 26 -‎ ‎（2）写出的表达式，将其化简，并根据等差数列的求和公式完成求解即可.‎ ‎【详解】解（1）∵对任意，有①‎ ‎∴当时，有，解得或2.‎ 当时，有②‎ ‎①②并整理得.‎ 而数列的各项均为正数，∴.‎ 当时，，此时成立；‎ 当时，，此时，不成立，舍去.‎ ‎∴.‎ ‎（2）.‎ ‎【点睛】本题考查利用递推关系求解通项公式、等比数列概念理解、公式法求和，属于综合问题，难度一般.注意利用求解通项公式.‎ ‎19.2019年上半年我国多个省市暴发了“非洲猪瘟”疫情，生猪大量病死，存栏量急剧下降，一时间猪肉价格暴涨，其他肉类价格也跟着大幅上扬，严重影响了居民的生活.为了解决这个问题，我国政府一方面鼓励有条件的企业和散户防控疫情，扩大生产；另一方面积极向多个国家开放猪肉进口，扩大肉源，确保市场供给稳定.某大型生猪生产企业分析当前市场形势，决定响应政府号召，扩大生产决策层调阅了该企业过去生产相关数据，就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表：‎ 生猪存栏数量（千头）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 头猪每天平均成本（元）‎ ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.9‎ ‎1.5‎ - 26 -‎ ‎（1）研究员甲根据以上数据认为与具有线性回归关系，请帮他求出关于的线.性回归方程（保留小数点后两位有效数字）‎ ‎（2）研究员乙根据以上数据得出与的回归模型：.为了评价两种模型的拟合效果，请完成以下任务：‎ ‎①完成下表（计算结果精确到0.01元）（备注：称为相应于点的残差）；‎ 生猪存栏数量（千头）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 头猪每天平均成本（元）‎ ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.9‎ ‎1.5‎ 模型甲 估计值 残差 模型乙 估计值 ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.76‎ ‎1.4‎ 残差 ‎0‎ ‎0‎ ‎0‎ ‎0.14‎ ‎0.1‎ ‎②分别计算模型甲与模型乙的残差平方和及，并通过比较的大小，判断哪个模型拟合效果更好.‎ ‎（3）根据市场调查，生猪存栏数量达到1万头时，饲养一头猪每一天的平均收入为7.5元；生猪存栏数量达到1.2万头时，饲养一头猪每一天的平均收入为7.2元若按（2）中拟合效果较好的模型计算一天中一头猪的平均成本，问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.（利润=收入-成本）‎ 参考公式：.‎ 参考数据：.‎ - 26 -‎ ‎【答案】（1）； （2）模型的拟合效果更好； （3）选择生猪存栏数量1.2万头能获得更多利润.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用公式直接计算得到答案.‎ ‎（2）计算得到，得到答案.‎ ‎（3）根据模型分别计算利润，比较大小得到答案.‎ 详解】（1）由题知：，，‎ ‎，故.‎ ‎（2）①经计算，可得下表：‎ 生猪存栏数量（千头）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 头猪每天平均成本（元）‎ ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.9‎ ‎1.5‎ 模型甲 估计值 ‎2.80‎ ‎2.55‎ ‎2.30‎ ‎2.05‎ ‎1.30‎ 残差 ‎0.40‎ ‎0.20‎ 模型乙 估计值 ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.76‎ ‎1.4‎ 残差 ‎0‎ ‎0‎ ‎0‎ ‎0.14‎ ‎0.1‎ ‎，‎ 因为，故模型的拟合效果更好.‎ - 26 -‎ ‎（3）若生猪存栏数量达到1万头，由（2）模型乙可知，每头猪的成本为元，‎ 这样一天获得的总利润为（元）；‎ 若生猪存栏数量达到1.2万头，由（2）模型乙可知，每头猪的成本为元，‎ 这样一天获得的总利润为（元），‎ 因为，所以选择生猪存栏数量1.2万头能获得更多利润.‎ ‎【点睛】本题考查了回归方程的计算和应用，意在考查学生的计算能力和应用能力.‎ ‎20.已知抛物线的焦点为F，点P为抛物线C上一点，，O为坐标原点，.‎ ‎（1）求抛物线C的方程；‎ ‎（2）设Q为抛物线C的准线上一点，过点F且垂直于OQ的直线交抛物线C于A，B两点记，的面积分别为，求的取值范围.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)根据可知直线的倾斜角为,再利用几何关系求得,代入抛物线方程化简即可.‎ ‎(2)设直线的方程为,再分别计算关于的表达式,进而求得关于的表达式再求范围即可.‎ ‎【详解】解：（1）由题可知,直线的倾斜角为,故,‎ 代入方程可得,化简得,因为所以 - 26 -‎ 故抛物线C的方程为 ‎（2）显然直线斜率不为0,故设直线的方程为,‎ 联立.设.则,.所以 设则因为直线垂直于OQ.故.所以 又到直线：的距离.‎ 故.‎ 故.‎ 设,则 当且仅当即时取等号.又,‎ 所以.‎ ‎【点睛】本题主要考查了抛物线中的弦长关系,同时也考查了直线与抛物线中的三角形面积问题,需要根据题意设方程联立,求出对应的面积的表达式再求最值,属于难题.‎ ‎21.已知函数,其中 为自然对数的底数.‎ ‎(1)当时，讨论函数的单调性;‎ ‎(2)当时，求证:对任意的.‎ ‎【答案】(1)在上单调递减.‎ ‎(2)证明见及解析.‎ - 26 -‎ ‎【解析】‎ ‎【详解】分析：(1)将代入 ，对函数求导即可判定函数的单调性．‎ ‎(2)将不等式转化为关于的一次函数，讨论在时一次函数对任意的两个端点都小于0，即可证明．‎ 详解：‎ ‎(1) ‎ ‎;‎ ‎∴在上单调递减 ‎(2)要证对恒成立 即证;对恒成立 令 即证当时，恒成立 即证;成立 ‎∵‎ ‎∴①式成立 现证明②式成立:‎ 令 设在,使得,则 在単调递增, 在単调递減 ‎∴,‎ ‎=‎ - 26 -‎ ‎∵，∴ ∴‎ 综上所述.在, 恒成立.‎ 点睛：函数与导数的综合应用，是高考的热点和难点，充分理解导数与单调性、极值、最值的关系，证明在一定条件下不等式成立，解不等式或求参数的取值情况，属于难题．‎ ‎（二）选做题（共10分，请考生在22，23题中任选一题做答）‎ ‎22.在平面直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求曲线的极坐标方程以及曲线的直角坐标方程；‎ ‎（2）若直线与曲线、曲线在第一象限交于两点，且，点的坐标为，求的面积.‎ ‎【答案】（1）的极坐标方程为，的直角坐标方程为（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先把曲线的参数方程消参后，转化为普通方程，再利用 求得极坐标方程.将，化为，再利用 求得曲线的普通方程.‎ ‎（2）设直线的极角，代入，得，将 - 26 -‎ 代入，得，由，得，即，从而求得，，从而求得，再利用求解.‎ ‎【详解】（1）依题意，曲线，即，‎ 故，即.‎ 因为，故，‎ 即，即.‎ ‎（2）将代入，得，‎ 将代入，得，‎ 由，得，得，‎ 解得，则.‎ 又，故，‎ 故的面积.‎ ‎【点睛】本题考查极坐标方程与直角坐标方程、参数方程与普通方程的转化、极坐标的几何意义，还考查推理论证能力以及数形结合思想，属于中档题.‎ ‎23.已知，，不等式恒成立.‎ ‎（1）求证:‎ ‎（2）求证:.‎ ‎【答案】（1）证明见解析（2）证明见解析 - 26 -‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先根据绝对值不等式求得的最大值，从而得到，再利用基本不等式进行证明；‎ ‎（2）利用基本不等式变形得，两边开平方得到新的不等式，利用同理可得另外两个不等式，再进行不等式相加，即可得答案.‎ ‎【详解】（1）∵，∴.‎ ‎∵，，，‎ ‎∴，‎ ‎∴，‎ ‎∴.‎ ‎（2）∵，，‎ 即两边开平方得.‎ 同理可得，.‎ 三式相加，得.‎ ‎【点睛】本题考查绝对值不等式、应用基本不等式证明不等式，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和推理论证能力.‎ - 26 -‎ - 26 -‎