2018年四川省德阳市高考数学一诊试卷（文科） 23页

‎2018年四川省德阳市高考数学一诊试卷（文科）‎ ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1．（5分）已知集合A={x|3x2﹣4x+1≤0}，B=，则A∩B=（　　）‎ A． B． C． D．‎ ‎2．（5分）若复数z满足z（1﹣i）=|1﹣i|+i（其中i为虚数单位），则z的虚部为（　　）‎ A． B． C．i D．i ‎3．（5分）已知函数f（x）=sin（ωx+）（ω＞0）满足：∀x1，x2∈R，当|f（x1）﹣f（x2）|=2时，|x1﹣x2|min=，那么f（x）的最小正周期是（　　）‎ A． B． C．π D．2π ‎4．（5分）已知函数f（x）在R上存在导数f′（x），下列关于f（x），f′（x）的描述正确的是（　　）‎ A．若f（x）为奇函数，则f′（x）必为奇函数 B．若f（x）为周期函数，则f′（x）必为周期函数 C．若f（x）不为周期函数，则f′（x）必不为周期函数 D．若f（x）为偶函数，则f′（x）必为偶函数 ‎5．（5分）如图的平面图形由16个全部是边长为1且有一个内角为60°的菱形组成，那么图形中的向量，满足•=（　　）‎ A．1 B．2 C．4 D．6‎ ‎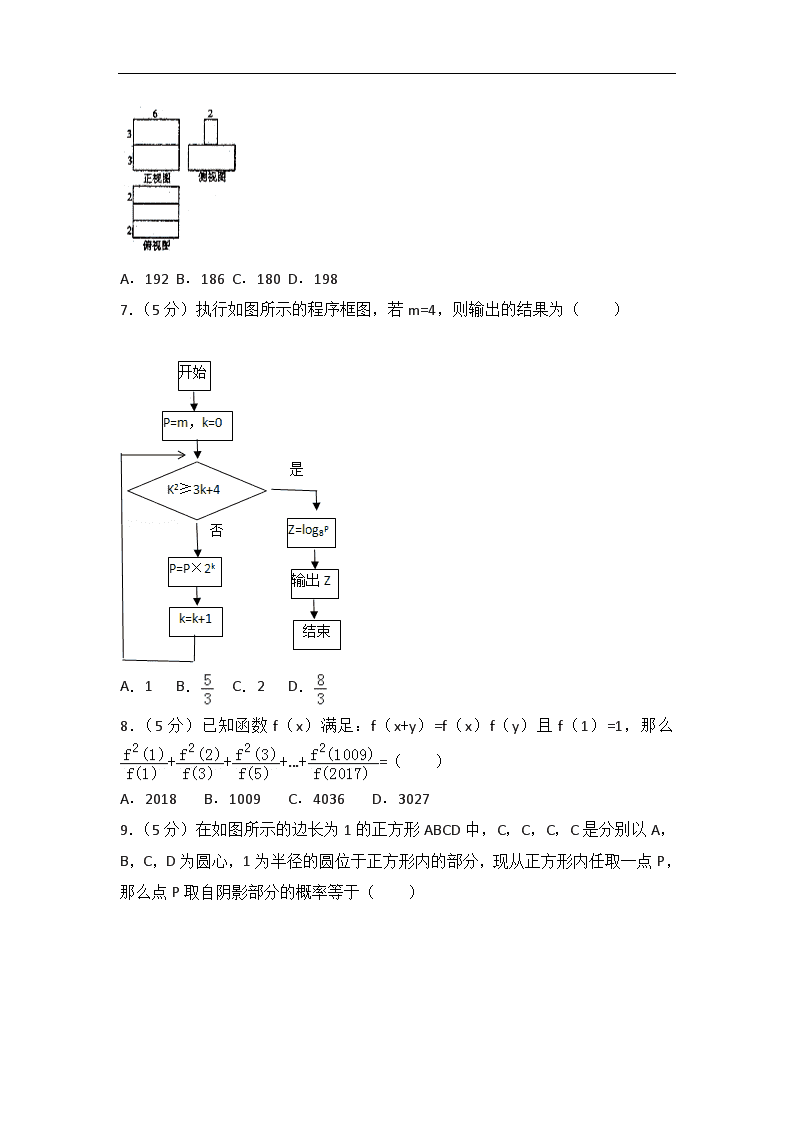6．（5分）榫卯是在两个木构件上所采用的一种凹凸结合的连接方式，凸出部分叫榫，凹进部分叫卯，榫和卯咬合，起到连接作用，代表建筑有：北京的紫禁城、天坛祈年殿、山西悬空寺等，如图所示是一种榫卯的三视图，其表面积为（　　）‎ A．192 B．186 C．180 D．198‎ ‎7．（5分）执行如图所示的程序框图，若m=4，则输出的结果为（　　）‎ A．1 B． C．2 D．‎ ‎8．（5分）已知函数f（x）满足：f（x+y）=f（x）f（y）且f（1）=1，那么+++…+=（　　）‎ A．2018 B．1009 C．4036 D．3027‎ ‎9．（5分）在如图所示的边长为1的正方形ABCD中，C，C，C，C是分别以A，B，C，D为圆心，1为半径的圆位于正方形内的部分，现从正方形内任取一点P，那么点P取自阴影部分的概率等于（　　）‎ A． B．﹣ C．﹣ D．﹣‎ ‎10．（5分）设点P为椭圆C：+=1上一点，F1、F2分别是椭圆C的左、右焦点，且△PF1F2的重心为点G，若|PF1|：|PF2|=3：4，那么△GPF1的面积为（　　）‎ A．24 B．12 C．8 D．6‎ ‎11．（5分）用min{a，b}表示实数a，b中的较小者，已知向量，，满足||=1，||=2，•=0，=λ+μ（λ+μ=1），则当min{•，•}取得最大值时，||=（　　）‎ A． B． C．1 D．‎ ‎12．（5分）已知函数f（x）=，x∈（﹣1，+∞），若关于x的方程f2（x）+m|f（x）|+2m+3=0有三个不同的实数解，则m的取值范围是（　　）‎ A．（﹣，0） B．（﹣，﹣） C．（﹣，﹣] D．（﹣，0）‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．（5分）已知函数f（x）=2x﹣e+1的图象经过点（1，3），那么f（log23）=　 　．‎ ‎14．（5分）为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（10分制）的频数分布统计图如图所示，如果得分值的中位数为a，众数为b，平均数为c，则a、b、c中的最大者是　 　．‎ ‎15．（5分）若平面区域夹在两条平行直线之间，且这两条平行直线间的最短距离为，那么这两条平行直线的斜率是　 　．‎ ‎16．（5分）若函数f（x）﹣sin（x+φ）是偶函数，f（x）﹣cos（x+φ）是奇函数，已知存在点P（x1，f（x1）），Q（x1+，f（x1+）），使函数f（x）在P、Q点处的切线斜率互为倒数，那么cosφ=　 　．‎ ‎　‎ 三、解答题（本大题共5小题，共70分）‎ ‎17．（12分）已知{an}是等差数列，且a1=3，a4=12，数列{bn}满足b1=4，b4=20，且{bn﹣an}为等比数列．‎ ‎（1）求数列{an}和{bn}的通项公式；‎ ‎（2）求数列{bn}的前n项和Sn．‎ ‎18．（12分）已知△ABC中，∠B=60°，点D在BC边上，且AC=2．‎ ‎（1）若CD=，AD=2，求AB；‎ ‎（2）求△ABC的周长的取值范围．‎ ‎19．（12分）为使政府部门与群众的沟通日常化，某城市社区组织“网络在线问政”活动．2015年，该社区每月通过问卷形式进行一次网上问政；2016年初，社区随机抽取了60名居民，对居民上网参政议政意愿进行调查．已知上网参与问政次数与参与人数的频数分布如表：‎ 参与调查问卷次数 ‎[0，2）‎ ‎[2，4）‎ ‎[4，6）‎ ‎[6，8）‎ ‎[8，10）‎ ‎[10，12]‎ 参与调查问卷人数 ‎8‎ ‎14‎ ‎8‎ ‎14‎ ‎10‎ ‎6‎ 附：‎ P（k2＞k0）‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ k0‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ K2=‎ ‎（1）若将参与调查问卷不少于4次的居民称为“积极上网参政居民”，请你根据频数分布表，完成2×2列联表，据此调查你是否有99%的把握认为在此社区内“上网参政议政与性别有关”？‎ 男 女 合计 积极上网参政议政 ‎8‎ 不积极上网参政议政 合计 ‎40‎ ‎（2）从被调查的人中按男女比例随机抽取6人，再从选取的6人中选出3人参加政府听证会，求选出的3人为2男1女的概率．‎ ‎20．（12分）已知函数f（x）=﹣x3+ax2﹣bx（a，b∈R）．‎ ‎（1）当a=1时，若∀x＞0，都有f（x）≤bx2+x成立，求实数b的最小值；‎ ‎（2）若b=﹣3a2（a＞0）．若函数f（x）的极小值点和极大值点分别为x1，x2．‎ ‎①求f（x1），f（x2）；‎ ‎②当λ∈（0，1）时，求f（）的值域．‎ ‎21．（12分）已知函数f（x）=﹣ax2+lnx（a∈R）．‎ ‎（1）讨论f（x）的单调性；‎ ‎（2）若∃x∈（1，+∞），f（x）＞﹣a，求a的取值范围．‎ ‎　‎ 请考生在22、23二题中任选一题作答．‎ ‎22．（10分）已知曲线C的极坐标方程是ρ=4cosθ．以极点为原点，极轴为x的正半轴建立平面直角坐标系，直线l的参数方程是：（t为参数）．‎ ‎（1）将曲线C的极坐标方程化成直角坐标方程，将直线l的参数方程化成普通方程；‎ ‎（2）当m=0时，直线l与曲线C异于原点O的交点为A，直线ρ=﹣与曲线C异于原点O的交点为B，求三角形AOB的面积．‎ ‎23．已知函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，1]．‎ ‎（1）求m的值；‎ ‎（2）若a，b，c∈（0，+∞），且++=m，证明：a+2b+3c≥9．‎ ‎　‎ ‎2018年四川省德阳市高考数学一诊试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1．（5分）已知集合A={x|3x2﹣4x+1≤0}，B=，则A∩B=（　　）‎ A． B． C． D．‎ ‎【解答】解：∵集合A={x|3x2﹣4x+1≤0}={x|}，‎ B=={x|x}，‎ ‎∴A∩B={x|}=[，1]．‎ 故选：B．‎ ‎　‎ ‎2．（5分）若复数z满足z（1﹣i）=|1﹣i|+i（其中i为虚数单位），则z的虚部为（　　）‎ A． B． C．i D．i ‎【解答】解：∵复数z满足z（1﹣i）=|1﹣i|+i（其中i为虚数单位），‎ ‎∴z===+i．‎ 则z的虚部为．‎ 故选：A．‎ ‎　‎ ‎3．（5分）已知函数f（x）=sin（ωx+）（ω＞0）满足：∀x1，x2∈R，当|f（x1）﹣f（x2）|=2时，|x1﹣x2|min=，那么f（x）的最小正周期是（　　）‎ A． B． C．π D．2π ‎【解答】解：根据正弦型函数f（x）=sin（ωx+）的图象与性质知，‎ 对∀x1，x2∈R，当|f（x1）﹣f（x2）|=2时，|x1﹣x2|min=，‎ ‎∴f（x）的最小正周期是T=2×=π．‎ 故选：C．‎ ‎　‎ ‎4．（5分）已知函数f（x）在R上存在导数f′（x），下列关于f（x），f′（x）的描述正确的是（　　）‎ A．若f（x）为奇函数，则f′（x）必为奇函数 B．若f（x）为周期函数，则f′（x）必为周期函数 C．若f（x）不为周期函数，则f′（x）必不为周期函数 D．若f（x）为偶函数，则f′（x）必为偶函数 ‎【解答】解：对于A：例如：f（x）=x3为奇函数，则f′（x）=3x2，为偶函数，故A错误，‎ 对于B：f（x）是可导函数，则f（x+T）=f（x），两边对x求导得（x+T）′f'（x+T）=f'（x），‎ f'（x+T）=f'（x），周期为T．故若f（x）为周期函数，则f′（x）必为周期函数．故B正确，‎ 对于C：例如：f（x）=sinx+x不是周期函数，当f′（x）=cosx+1为周期函数，故C错误，‎ 对于D：例如：f（x）=x2为偶函数，则f′（x）=2x为奇函数，故D错误，‎ 故选：B．‎ ‎　‎ ‎5．（5分）如图的平面图形由16个全部是边长为1且有一个内角为60°的菱形组成，那么图形中的向量，满足•=（　　）‎ A．1 B．2 C．4 D．6‎ ‎【解答】解：如图，‎ 由题意可知，，且与的夹角为60°，‎ ‎∴=．‎ 则，，‎ ‎∴•==‎ ‎=．‎ 故选：D．‎ ‎　‎ ‎6．（5分）榫卯是在两个木构件上所采用的一种凹凸结合的连接方式，凸出部分叫榫，凹进部分叫卯，榫和卯咬合，起到连接作用，代表建筑有：北京的紫禁城、天坛祈年殿、山西悬空寺等，如图所示是一种榫卯的三视图，其表面积为（　　）‎ A．192 B．186 C．180 D．198‎ ‎【解答】解：由三视图还原原几何体，可知该几何体为组合体，上部分为长方体，棱长分别为2、6、3，下部分为长方体．棱长分别为6、6、3，‎ ‎ 其表面积公式S=4×6×3+2×6×6+（2+6）×2×2=192‎ 故选：A．‎ ‎　‎ ‎7．（5分）执行如图所示的程序框图，若m=4，则输出的结果为（　　）‎ A．1 B． C．2 D．‎ ‎【解答】解：模拟执行程序框图，可得 p=4，k=0‎ 不满足条件k2≥3k+4，p=4，k=1‎ 不满足条件k2≥3k+4，p=8，k=2‎ 不满足条件k2≥3k+4，p=32，k=3‎ 不满足条件k2≥3k+4，p=256，k=4‎ 满足条件k2≥3k+4，退出循环，可得z=‎ 故选：D．‎ ‎　‎ ‎8．（5分）已知函数f（x）满足：f（x+y）=f（x）f（y）且f（1）=1，那么+++…+=（　　）‎ A．2018 B．1009 C．4036 D．3027‎ ‎【解答】解：由意题f（x+y）=f（x）f（y），且f（1）=1，‎ 可得令x=n，y=1，可得f（n+1）=f（n），‎ 可得f（1）=f（2）=f（3）=…=f（n）=1，‎ 那么：+++…+=f2（1）+f2（2）+…+f2（1009）=1009．‎ 故选：B ‎　‎ ‎9．（5分）在如图所示的边长为1的正方形ABCD中，C，C，C，C是分别以A，B，C，D为圆心，1为半径的圆位于正方形内的部分，现从正方形内任取一点P，那么点P取自阴影部分的概率等于（　　）‎ A． B．﹣ C．﹣ D．﹣‎ ‎【解答】解：如图，‎ 由对称性可知，阴影部分所占面积为弓形BC1D面积的一半，‎ ‎∵正方形ABCD的边长为1，‎ 则扇形ABD的面积为，直角三角形ABD的面积为，‎ ‎∴阴影部分的面积为．‎ 又正方形ABCD的面积为1，‎ ‎∴从正方形内任取一点P，那么点P取自阴影部分的概率等于．‎ 故选：D．‎ ‎　‎ ‎10．（5分）设点P为椭圆C：+=1上一点，F1、F2分别是椭圆C的左、右焦点，且△PF1F2的重心为点G，若|PF1|：|PF2|=3：4，那么△GPF1的面积为（　　）‎ A．24 B．12 C．8 D．6‎ ‎【解答】解：∵点P为椭圆C：+=1上一点，|PF1|：|PF2|=3：4，|PF1|+|PF2|=2a=14‎ ‎∴|PF1|=6，|PF2|=8，又∵F1F2=2c=10，‎ ‎∴△PF1F2是直角三角形，S=，‎ ‎∵△PF1F2的重心为点G．∴S=，‎ ‎∴△GPF1的面积为8，‎ 故选：C ‎　‎ ‎11．（5分）用min{a，b}表示实数a，b中的较小者，已知向量，，满足||=1，||=2，•=0，=λ+μ（λ+μ=1），则当min{•，•}取得最大值时，||=（　　）‎ A． B． C．1 D．‎ ‎【解答】解：∵•=（λ+μ）•=λ+μ=λ，‎ ‎=（λ+μ）•=μ+λ=4μ=4﹣4λ，‎ 令λ≥4﹣4λ，解得λ≥‎ ‎∴min{•，•}=，‎ 设f（x）=，‎ 则f（x）在[0，]上递增，在[，1]上递减，‎ ‎∴当x=，f（x）取得最小值，‎ 此时=+，‎ ‎∴||2=（16+8•+）=，‎ ‎∴||=，‎ 故选：A．‎ ‎　‎ ‎12．（5分）已知函数f（x）=，x∈（﹣1，+∞），若关于x的方程f2（x）+m|f（x）|+2m+3=0有三个不同的实数解，则m的取值范围是（　　）‎ A．（﹣，0） B．（﹣，﹣） C．（﹣，﹣] D．（﹣，0）‎ ‎【解答】解：，y=|f（x）|，x∈（﹣1，+∞）的图象如下：‎ 设|f（x）|=t，则|f（x）|2+m|f（x）|+2m+3=0有三个不同的实数解，即为t2+mt+2m+3=0有两个根，‎ ‎①t=0时，代入t2+mt+2m+3=0得m=﹣，即，另一根为只有一个交点，舍去 ‎ ‎②一个在（0，1）上，一个在[1，+∞）上时，‎ 设h（t）=t2+mt+2m+3‎ ‎，解得﹣＜m≤﹣．‎ 故选：C ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．（5分）已知函数f（x）=2x﹣e+1的图象经过点（1，3），那么f（log23）=　4　．‎ ‎【解答】解：∵函数f（x）=2x﹣e+1的图象经过点（1，3），‎ ‎∴f（1）=21﹣e+1=3，解得e=0，‎ ‎∴f（x）=2x+1，‎ ‎∴f（log23）=+1=3+1=4．‎ 故答案为：4．‎ ‎　‎ ‎14．（5分）为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（10分制）的频数分布统计图如图所示，如果得分值的中位数为a，众数为b，平均数为c，则a、b、c中的最大者是　c　．‎ ‎【解答】解：由频率分布直方图知，众数为b=5；‎ 由中位数的定义知是第15个数与第16个数的平均值，‎ 将数据从小到大排第15 个数是5，第16个数是6，‎ ‎∴中位数为a==5.5；‎ 平均数是c=×（2×3+3×4+5×10+6×6+3×7+2×9+2×10）≈6.0，‎ ‎∴b＜a＜c，即a、b、c中最大者是c．‎ 故答案为：c．‎ ‎　‎ ‎15．（5分）若平面区域夹在两条平行直线之间，且这两条平行直线间的最短距离为，那么这两条平行直线的斜率是　1　．‎ ‎【解答】解：作出平面区域如图所示：‎ 可行域是等腰三角形，平面区域 夹在两条平行直线之间的距离为：，‎ 可得可行域的A（1，2），B（2，1），C（3，3），‎ ‎|AB|==，‎ ‎∴平行线间的距离的最小值为d=，‎ 所求直线与x+y﹣3=0垂直，可得：k=1．‎ 故答案为：1．‎ ‎　‎ ‎16．（5分）若函数f（x）﹣sin（x+φ）是偶函数，f（x）﹣cos（x+φ）是奇函数，已知存在点P（x1，f（x1）），Q（x1+，f（x1+）），使函数f（x）在P、Q点处的切线斜率互为倒数，那么cosφ=　±1　．‎ ‎【解答】解：函数f（x）﹣sin（x+φ）是偶函数，‎ 可得f（﹣x）﹣sin（﹣x+φ）=f（x）﹣sin（x+φ），‎ 即有f（﹣x）=f（x）﹣sinxcosφ﹣cosxsinφ﹣sinxcosφ+cosxsinφ=f（x）﹣2sinxcosφ，①‎ f（x）﹣cos（x+φ）是奇函数，‎ 可得f（﹣x）﹣cos（﹣x+φ）+f（x）﹣cos（x+φ）=0，‎ f（﹣x）+f（x）﹣cosxcosφ﹣sinxsinφ﹣cosxcosφ+sinxsinφ=0，‎ 即为f（﹣x）+f（x）﹣2cosxcosφ=0，②‎ 由①②可得f（x）=（sinx+cosx）cosφ，‎ 导数为f′（x）=（cosx﹣sinx）cosφ，‎ ‎∃x1，使得函数f（x）‎ 在点P（x1，f（x1）），Q（x1+，f（x1+））处的切线斜率互为倒数，‎ 可得f′（x1）•f′（x1+）=1，‎ 可得（cosx1﹣sinx1）cosφ•（cos（x1+）﹣sin（x1+））cosφ=1，‎ 即为（cosx1﹣sinx1）（﹣sinx1﹣cosx1）cos2φ=1，‎ 即为（sin2x1﹣cos2x1）cos2φ=1，‎ 即有﹣cos2x1•cos2φ=1，‎ 可得cos2φ=1，cos2x1=﹣1，‎ ‎∴cosφ=±1．‎ 故答案为：±1．‎ ‎　‎ 三、解答题（本大题共5小题，共70分）‎ ‎17．（12分）已知{an}是等差数列，且a1=3，a4=12，数列{bn}满足b1=4，b4=20，且{bn﹣an}为等比数列．‎ ‎（1）求数列{an}和{bn}的通项公式；‎ ‎（2）求数列{bn}的前n项和Sn．‎ ‎【解答】解：（1）{an}是等差数列，设数列的公差为d，且a1=3，a4=12，‎ 则：，‎ 所以数列的通项公式为：an=3+3（n﹣1）=3n．‎ 数列{bn}满足b1=4，b4=20，且{bn﹣an}为等比数列，设公比为q，‎ 则：，‎ 解得：q=2．‎ 所以数列的通项公式为：，‎ 整理得：．‎ ‎（2）由于：，‎ 则：Sn=3（1+2+…+n）+（20+21+…+2n﹣1），‎ ‎=，‎ ‎=．‎ ‎　‎ ‎18．（12分）已知△ABC中，∠B=60°，点D在BC边上，且AC=2．‎ ‎（1）若CD=，AD=2，求AB；‎ ‎（2）求△ABC的周长的取值范围．‎ ‎【解答】解：（1）△ABC中，∠B=60°，点D在BC边上，且AC=2．CD=，AD=2，‎ 则：=，‎ 所以：=．‎ 在△ABC中，利用正弦定理：‎ ‎，‎ 解得：=，‎ ‎（2）△ABC中，利用正弦定理得：=，‎ 所以：，=，‎ 由于：0＜A＜120°，‎ 则：l△ABC==，‎ ‎=2+，‎ ‎=，‎ 由于：0＜A＜120°，‎ 则：30°＜A+30°＜150°，‎ 得到：，‎ 所以△ABC的周长的范围是：‎ ‎　‎ ‎19．（12分）为使政府部门与群众的沟通日常化，某城市社区组织“网络在线问政”活动．2015年，该社区每月通过问卷形式进行一次网上问政；2016年初，社区随机抽取了60名居民，对居民上网参政议政意愿进行调查．已知上网参与问政次数与参与人数的频数分布如表：‎ 参与调查问卷次数 ‎[0，2）‎ ‎[2，4）‎ ‎[4，6）‎ ‎[6，8）‎ ‎[8，10）‎ ‎[10，12]‎ 参与调查问卷人数 ‎8‎ ‎14‎ ‎8‎ ‎14‎ ‎10‎ ‎6‎ 附：‎ P（k2＞k0）‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ k0‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ K2=‎ ‎（1）若将参与调查问卷不少于4次的居民称为“积极上网参政居民”，请你根据频数分布表，完成2×2列联表，据此调查你是否有99%的把握认为在此社区内“上网参政议政与性别有关”？‎ 男 女 合计 积极上网参政议政 ‎8‎ 不积极上网参政议政 合计 ‎40‎ ‎（2）从被调查的人中按男女比例随机抽取6人，再从选取的6人中选出3人参加政府听证会，求选出的3人为2男1女的概率．‎ ‎【解答】解：（1）由题意知积极上网参政的有：8+14+10+6=38人，‎ 不积极上网参政的有8+14=22人，‎ ‎2×2列联表为：‎ ‎ ‎ ‎ 男 ‎ 女 合计 ‎ ‎ 积极上网参政居民 ‎ 30‎ ‎ 8‎ ‎ 38‎ 不积极上网参政居民 ‎ ‎ 10‎ ‎ 12‎ ‎ 22‎ 合计 ‎ ‎ 40‎ ‎ 20‎ ‎ 60‎ ‎∴K2=≈7.03，∵7.03＞6.635，‎ ‎∴有99%的把握认为“上网参政与性别有关”．‎ ‎（2）选取男居民人数为6×=4人，‎ 选取女居民人数为6×，‎ 记4个男居民为A，B，C，D，2个女居民为甲，乙，‎ 从选取的6人中选出3人参加政府听证会，基本事件总数有20种，分别为：‎ ‎（A，B，C），（A，B，D），（A，B，甲），（A，B，乙），（A，C，D），（A，C，甲），（A，C，乙），‎ ‎（A，D，甲），（A，D，乙），（A，甲，乙），（B，C，D），（B，C，甲），（B，C，乙），（B，D，甲），‎ ‎（B，D，乙），（B，甲，乙），（C，D，甲），（C，D，乙），（C，甲，乙），（D，甲，乙），‎ 选出的3人恰为2男1女的有12种，‎ ‎∴选出的3人恰为2男1女的概率为：p=．‎ ‎　‎ ‎20．（12分）已知函数f（x）=﹣x3+ax2﹣bx（a，b∈R）．‎ ‎（1）当a=1时，若∀x＞0，都有f（x）≤bx2+x成立，求实数b的最小值；‎ ‎（2）若b=﹣3a2（a＞0）．若函数f（x）的极小值点和极大值点分别为x1，x2．‎ ‎①求f（x1），f（x2）；‎ ‎②当λ∈（0，1）时，求f（）的值域．‎ ‎【解答】解：（1）当a=1时，∀x＞0，都有f（x）≤bx2+x成立，⇔+x2﹣bx≤bx2+x⇔b≥（x＞0）．‎ 令t=x+1＞1．∴b≥=﹣（t＞1）．‎ ‎∵t＞1，t+=2，当且仅当t=时取等号．∴﹣≤（t＞1）．‎ ‎∴b的最小值为：（t＞1）．‎ ‎（2）b=﹣3a2（a＞0）．f（x）=﹣x3+ax2+3a2x，‎ f′（x）=﹣x2+2ax+3a2=﹣（x﹣3a）（x+a），令f′（x）=0，解得x=3a，或﹣a．‎ ‎∵a＞0，可得函数f（x）在（﹣∞，﹣a）上单调递减；在（﹣a，3a）上单调递增；（3a，+∞）上单调递减．‎ ‎∴f（x）的极小值=f（﹣a）=﹣，f（x）的极大值=f（3a）=9a3．‎ ‎②由①可知：x1=﹣a，x2=3a．∴=x2+（x1﹣x2），λ∈（0，1），（x1﹣x2）∈（x1﹣x2，），‎ 故∈⊆（x1，x2）．‎ 由①可得：f（x）在（x1，x2）上单调递增，∴f（）的值域是=（f（﹣a），f（a））=．‎ ‎　‎ ‎21．（12分）已知函数f（x）=﹣ax2+lnx（a∈R）．‎ ‎（1）讨论f（x）的单调性；‎ ‎（2）若∃x∈（1，+∞），f（x）＞﹣a，求a的取值范围．‎ ‎【解答】解：（1）由f（x）=﹣ax2+lnx，得f′（x）=﹣2ax+=（x＞0），‎ 当a≤0时，f′（x）＞0，f（x）在（0，+∞）上为增函数；‎ 当a＞0时，由f′（x）=0，得=﹣＜0，=＞0，‎ ‎∴当x∈（0，）时，f′（x）＞0，f（x）为增函数，当x∈（）时，f′（x）＜0，f（x）为减函数；‎ ‎（2）当a≤0时，若x∈（1，+∞），则f（x）+a=﹣ax2+lnx+a=a（1﹣x2）+lnx＞0，满足题意；‎ 当a＞0时，由（1）知，当，即a时，f（x）在（1，+∞）上为减函数，此时f（x）max=f（1）=﹣a，﹣a＞﹣a不成立；‎ 当，即0＜a＜时，f（x）在（1，）上为增函数，在（，+∞）上为减函数，‎ 此时=，‎ 由，得1+ln2a＜2a，‎ 令g（a）=1+ln2a﹣2a，则g′（a）=，‎ 则g（a）在（0，）上为增函数，∴g（a）＜g（）=0，即1+ln2a＜2a恒成立，‎ ‎∴0＜a＜．‎ 综上，若∃x∈（1，+∞），使得f（x）＞﹣a，a的取值范围为a．‎ ‎　‎ 请考生在22、23二题中任选一题作答．‎ ‎22．（10分）已知曲线C的极坐标方程是ρ=4cosθ．以极点为原点，极轴为x的正半轴建立平面直角坐标系，直线l的参数方程是：（t为参数）．‎ ‎（1）将曲线C的极坐标方程化成直角坐标方程，将直线l的参数方程化成普通方程；‎ ‎（2）当m=0时，直线l与曲线C异于原点O的交点为A，直线ρ=﹣与曲线C异于原点O的交点为B，求三角形AOB的面积．‎ ‎【解答】解：（1）线C的极坐标方程是ρ=4cosθ．‎ 转化为直角坐标方程为：x2+y2=4x 直线的参数方程，‎ 转化为直角坐标方程为：y=x﹣m．‎ ‎（2）当m=0时，‎ 求得：A（2，），B（2，﹣），‎ 所以：=．‎ ‎　‎ ‎23．已知函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，1]．‎ ‎（1）求m的值；‎ ‎（2）若a，b，c∈（0，+∞），且++=m，证明：a+2b+3c≥9．‎ ‎【解答】解：（1）函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，1]，‎ 可得m﹣|x|≥0的解集为[﹣1，1]，即有[﹣m，m}={﹣1，1]，‎ 可得m=1；‎ ‎（2）证明：a，b，c∈（0，+∞），且++=1，‎ 则a+2b+3c=（a+2b+3c）（++）‎ ‎=3+（+）+（+）+（+）‎ ‎≥3+2+2+2‎ ‎=3+2+2+2=9，‎ 当且仅当a=2b=3c=3，取得等号．‎ ‎　‎