高中数学必修4教案：1_2_1任意角的三角函数（2） 4页

‎ ‎1.2.1‎ 任意角的三角函数< 第二课时>‎ 班级 姓名 ‎ 学习目标 ‎ 1.通过对任意角的三角函数定义的理解,掌握终边相同角的同一三角函数值相等.‎ ‎ 2.正确利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值表示出来,即用正弦线、余弦线、正切线表示出来.‎ 重点难点 教学重点 终边相同的角的同一三角函数值相等 教学难点 利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值用几何形式表示.‎ 教学过程 （一） 复习提问 1、 三角函数（正弦，余弦，正切函数）的概念。（两个定义）‎ 2、 三角函数（正弦，余弦，正切函数）的定义域。‎ 3、 三角函数（正弦，余弦，正切函数）值在各象限的符号。‎ ‎4、<小结>常见常用角的三角函数值 角 ‎30º ‎45º ‎60°‎ ‎120°‎ ‎135°‎ ‎150°‎ 角的弧度数 sin cos tan 角α ‎0°‎ ‎90°‎ ‎180°‎ ‎270°‎ ‎360°‎ 角α的弧度数 sinα cosα tanα ‎（二）新知探究 ‎1、问题 ：如果两个角的终边相同，那么这两个角的同一三角函数值有何关系？ ‎ ‎2、求下列三角函数值 (1)sin420°; (2) sin60°‎ ‎ 3、结论 由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.由此得到一组公式(公式一): ‎ sin(α+k·2π)=sinα,‎ cos(α+k·2π)=cosα,‎ tan(α+k·2π)=tanα,‎ 其中k∈Z.‎ ‎（作用）利用公式一,可以把求任意角的三角函数值,转化为求0到2π(或0°到360°)角的三角函数值.这个公式称为三角函数的“诱导公式一”.‎ ‎4.例题讲解 例1、确定下列三角函数值的符号：（1）sin(-392°) (2)tan(-)‎ ‎ ‎ 练习(1)、确定下列三角函数值的符号： （1）tan(-672°) (2)sin1480°10¹ (3)cos ‎ 例2、求下列三角函数值 (1)sin390°; (2)cos; (3)tan(-690°).‎ 练习(2)、求下列三角函数值 (1)sin420°; (2)cos; (3)tan(-330°).‎ ‎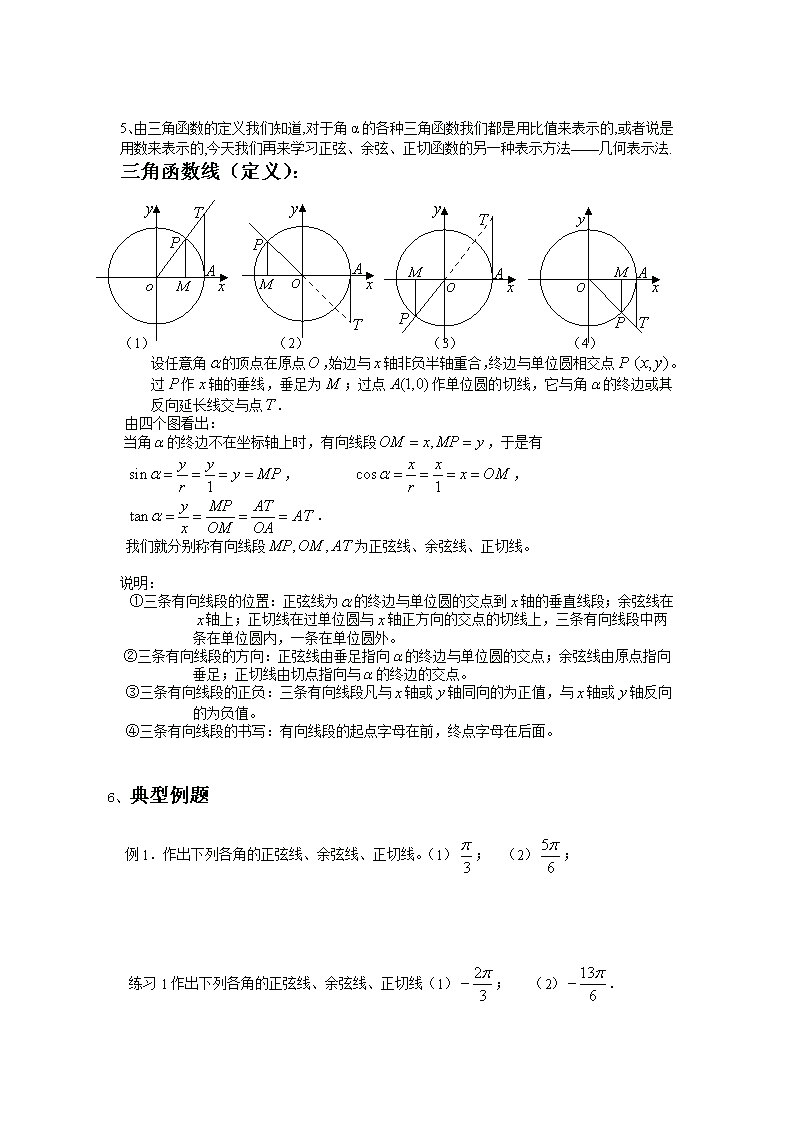5、由三角函数的定义我们知道,对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的,今天我们再来学习正弦、余弦、正切函数的另一种表示方法——几何表示法.‎ 三角函数线（定义）：‎ ‎ ‎ ‎（1） （2） （3） （4）‎ 设任意角的顶点在原点，始边与轴非负半轴重合，终边与单位圆相交点。过作轴的垂线，垂足为；过点作单位圆的切线，它与角的终边或其反向延长线交与点.‎ 由四个图看出：‎ 当角的终边不在坐标轴上时，有向线段，于是有 ‎， ，‎ ‎．‎ 我们就分别称有向线段为正弦线、余弦线、正切线。‎ 说明：‎ ‎①三条有向线段的位置：正弦线为的终边与单位圆的交点到轴的垂直线段；余弦线在轴上；正切线在过单位圆与轴正方向的交点的切线上，三条有向线段中两条在单位圆内，一条在单位圆外。‎ ‎②三条有向线段的方向：正弦线由垂足指向的终边与单位圆的交点；余弦线由原点指向 垂足；正切线由切点指向与的终边的交点。‎ ‎③三条有向线段的正负：三条有向线段凡与轴或轴同向的为正值，与轴或轴反向 的为负值。‎ ‎④三条有向线段的书写：有向线段的起点字母在前，终点字母在后面。‎ ‎6、典型例题 例1．作出下列各角的正弦线、余弦线、正切线。（1）； （2）； ‎ 练习1作出下列各角的正弦线、余弦线、正切线（1）； （2）．‎ ‎7、课下探究 （1） 利用三角函数线比较下列各组数的大小：‎ ‎1° 与 2° tan与tan ‎ ‎（2）利用单位圆寻找适合下列条件的0°到360°的角 x y o T A ‎210° ‎30° x y o P1‎ P2‎ ‎1° sina≥ 2° tana ‎（三）课堂小结、‎ 本节课你学了哪些知识？有哪些收获？你已经正确理解、掌握它们了吗？‎ ‎（四）课后作业 习题1.2A组第3,4题