2021届高考数学一轮复习第七章解析几何第4讲直线与圆的位置关系课件 43页

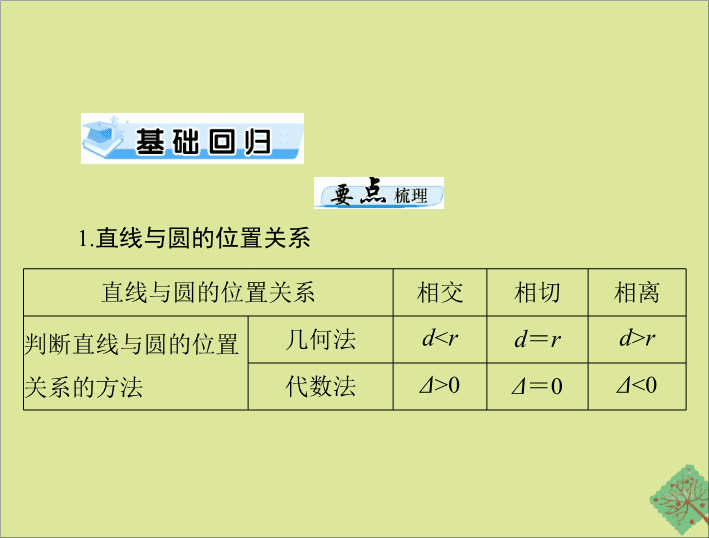
第 4 讲 直线与圆的位置关系 课标要求 考情风向标 1. 能根据给定直线、圆的方 程，判断直线与圆、圆与圆 的位置关系 . 2. 能用直线和圆的方程解决 一些简单的问题 . 3. 在平面解析几何初步的学 习过程中，体会用代数方法 处理几何问题的思想 从近几年的高考看，对这部分内容 的考查呈上升的趋势，逐渐成为热 点问题，要引起重视 . 预计 2021 年 高考仍将以圆与圆、直线与圆的位 置为主要考点，尤其是直线与圆的 位置关系是重中之重， 备考时应特 别关注利用圆心到直线的距离与 半径的大小比较来判断位置关系 及有关计算的方法 直线与圆的位置关系 相交 相切 相离 判断直线与圆的位置关系的方法 几何法 d < r d ＝ r d > r 代数法 Δ >0 Δ ＝ 0 Δ <0 1. 直线与圆的位置关系 圆与圆的位置 关系 内含 内切 相交 外切 外离 判断圆与圆的 位置关系的方 法 ( r < R ) d < R － r d ＝ R － r R － r < d < R ＋ r d ＝ R ＋ r d > R ＋ r 公切线条数 0 1 2 3 4 2. 两圆的位置关系 3. 计算直线被圆截得的弦长的常用方法 (1) 几何方法：运用弦心距 ( 即圆心到直线的距离 ) 、弦长的 一半及半径构成的直角三角形计算 . (2) 代数方法：运用韦达定理及弦长公式： 说明：圆的弦长、弦心距的计算常用几何方法 . 4. 圆的切线方程常用结论 (1) 过圆 x 2 ＋ y 2 ＝ r 2 上一点 P ( x 0 ， y 0 ) 的圆的切线方程为 x 0 x ＋ y 0 y ＝ r 2 . (2) 过圆 ( x － a ) 2 ＋ ( y － b ) 2 ＝ r 2 上一点 P ( x 0 ， y 0 ) 的圆的切线方 程为 ( x 0 － a )( x － a ) ＋ ( y 0 － b )( y － b ) ＝ r 2. (3) 过圆 x 2 ＋ y 2 ＝ r 2 外一点 M ( x 0 ， y 0 ) 作圆的两条切线，则两 切点所在直线方程为 x 0 x ＋ y 0 y ＝ r 2 . 1. 已知直线 l ： x ＋ ay － 1 ＝ 0( a ∈ R ) 是圆 C ： x 2 ＋ y 2 － 4 x － 2 y ＋ 1 ＝ 0 的对称轴 . 过点 A ( － 4 ， a ) 作圆 C 的一条切线，切点为 B ， 则 | AB | ＝ ( ) C 2. 已知圆 x 2 ＋ y 2 ＋ 2 x － 2 y ＋ a ＝ 0 截直线 x ＋ y ＋ 2 ＝ 0 所得弦 的长度为 4 ，则实数 a 的值为 ( ) A. － 2 B. － 4 C. － 6 D. － 8 B 3. 已知直线 x － y ＋ a ＝ 0 与圆心为 C 的圆 x 2 ＋ y 2 ＋ 2 x － 4 y － 4 ＝ 0 相交于 A ， B 两点，且 AC ⊥ BC ，则实数 a 的值为 __ ______ . 0 或 6 4.(2019 年浙江 ) 已知圆 C 的圆心坐标是 (0 ， m ) ，半径长是 r . 若直线 2 x － y ＋ 3 ＝ 0 与圆相切于点 A ( － 2 ，－ 1) ，则 m ＝ ______ ， r ＝ ________. － 2 考点 1 直线与圆的位置关系 考向 1 直线与圆位置关系的判断 例 1 ： (1) 若直线 4 x － 3 y ＋ a ＝ 0 与圆 x 2 ＋ y 2 ＝ 100 有如下关 系： ① 相交； ② 相切； ③ 相离 . 试分别求实数 a 的取值范围 . Δ ＝ (8 a ) 2 － 4×25( a 2 － 900) ＝－ 36 a 2 ＋ 90 000. ① 当直线 和圆相交时， Δ >0 ， 即－ 36 a 2 ＋ 90 000>0 ， － 50< a <50 ； ② 当直线和圆相切时， Δ ＝ 0 ，即 a ＝ 50 或 a ＝－ 50 ； ③ 当直线和圆相离时， Δ <0 ，即 a < － 50 或 a >50. 方法二 ( 几何法 ) ， 圆 x 2 ＋ y 2 ＝ 100 的圆心为 (0,0) ，半径 r ＝ 10 ， (2)(2019 年福建漳州八校联考 ) 已知点 P ( a ， b )( ab ≠0) 是圆 x 2 ＋ y 2 ＝ r 2 内的一点，直线 m 是以 P 为中点的弦所在的直线， 直线 l 的方程为 ax ＋ by ＝ r 2 ，那么 ( ) A. m ∥ l ，且 l 与圆相交 B. m ⊥ l ，且 l 与圆相切 C. m ∥ l ，且 l 与圆相离 D. m ⊥ l ，且 l 与圆相离 答案： C 【 规律方法 】 判断直线与圆位置关系的三种方法： ① 几何法：由圆心到直线的距离 d 与圆的半径 r 的大小关 系判断； ② 代数法：根据直线与圆的 方程组成的方程组解的个 数来判断； ③ 直线系法：若直线恒过定点，可通过判断点与圆 的位置关系判断，但有一定的局限性，必须是过定点的直线系 . 考向 2 切线问题 例 2 ： 过点 A ( － 1,4) 作圆 ( x － 2) 2 ＋ ( y － 3) 2 ＝ 1 的切线 l ，求 切线 l 的方程 . 解： ∵ ( － 1 － 2) 2 ＋ (4 － 3) 2 ＝ 10 ＞ 1 ， ∴ 点 A 在圆外 . 方法一，当直线 l 的斜率不存在时， 直线 l 的方程是 x ＝－ 1 ， 不满足题意 . 设切线 l 的斜率为 k ，则方程为 y － 4 ＝ k ( x ＋ 1). 消去 y ，得到关于 x 的一元二次方程 (1 ＋ k 2 ) x 2 ＋ (2 k 2 ＋ 2 k － 4) x ＋ k 2 ＋ 2 k ＋ 4 ＝ 0 ， 则 Δ ＝ (2 k 2 ＋ 2 k － 4) 2 － 4(1 ＋ k 2 )( k 2 ＋ 2 k ＋ 4) ＝ 0. 化简，得 4 k 2 ＋ 3 k ＝ 0. 因此，所求切线 l 的方程为 y ＝ 4 或 3 x ＋ 4 y － 13 ＝ 0. 【 规律方法 】 (1) 过圆上一点 ( x 0 ， y 0 ) 的圆的切线方程的求法： 先求切点与圆心连线的斜率 k ，再由垂直关系得切线的斜率为 图形可直接得切线方程为 y ＝ y 0 或 x ＝ x 0 . (2) 过圆外一点 ( x 0 ， y 0 ) 的圆的切线方程的求法： 设切线方程为 y － y 0 ＝ k ( x － x 0 ) ，由圆心到直线的距离等于 半径建立方程，可求得 k ，也就得切线方程 . 当用此法只求出一 个方程时，另一个方程应为 x ＝ x 0 ，因为在上面解法中不包括斜 率不存在的情况，而过圆外一点的切线有两条 . 一般不用联立方 程组的方法求解 . 【 跟踪训练 】 1.(2015 年山东 ) 一条光线从点 ( － 2 ，－ 3) 射出，经 y 轴反射 后与圆 ( x ＋ 3) 2 ＋ ( y － 2) 2 ＝ 1 相切，则反射光线所在直线的斜率为 ( ) 答案： D 考向 3 弦长问题 例 3 ： (1) (2018 年新课标 Ⅰ ) 直线 y ＝ x ＋ 1 与圆 x 2 ＋ y 2 ＋ 2 y － 3 ＝ 0 交于 A ， B 两点，则 | AB | ＝ ________. (2)(2015 年新课标 Ⅱ ) 过三点 A (1, 3) ， B (4,2) ， C (1 ，－ 7) 的 圆交 y 轴于 M ， N 两点，则 | MN | ＝ ( ) 答案： C (3) 过点 ( － 4,0) 作直线 l 与圆 x 2 ＋ y 2 ＋ 2 x － 4 y － 20 ＝ 0 交于 A ， ) B 两点，若 | AB | ＝ 8 ，则直线 l 的方程为 ( A.5 x ＋ 12 y ＋ 20 ＝ 0 B.5 x ＋ 12 y ＋ 20 ＝ 0 或 x ＋ 4 ＝ 0 C.5 x － 12 y ＋ 20 ＝ 0 D.5 x － 12 y ＋ 20 ＝ 0 或 x ＋ 4 ＝ 0 答案： B 【 规律方法 】 关于圆的弦长问题，可用几何法从半径、弦 心距、弦长的一半所组成的直角三角形求解，也可用代数法的 弦长公式求解 . 考点 2 圆与圆的位置关系 例 4 ： (1) (2019 年河北衡水模拟 ) 圆 C 1 ： ( x ＋ 1) 2 ＋ ( y － 2) 2 ＝ 4 与圆 C 2 ： ( x － 3) 2 ＋ ( y － 2) 2 ＝ 4 的公切线的条数是 ( ) A.1 B.2 C.3 D.4 解析 ： 圆 C 1 ： ( x ＋ 1) 2 ＋ ( y － 2) 2 ＝ 4 的圆心为 ( － 1,2) ，半径 为 2 ，圆 C 2 ： ( x － 3) 2 ＋ ( y － 2) 2 ＝ 4 的圆心为 (3,2) ，半径为 2 ，两 心距等于两圆的半径之和，故两圆相外切，故公切线的条数为 3. 答案： C (2) 已知圆 M ： x 2 ＋ y 2 － 2 ay ＝ 0( a >0) 截直线 x ＋ y ＝ 0 所得线 ) 关系是 ( A. 内切 C. 外切 B. 相交 D. 相离 答案： B (3) 若 ⊙ O ： x 2 ＋ y 2 ＝ 5 与 ⊙ O 1 ： ( x － m ) 2 ＋ y 2 ＝ 20( m ∈ R ) 相交 于 A ， B 两点，且两圆在点 A 处的切线互相垂直，则线段 AB 的 长度是 ________. 解析： 由题意 ⊙ O 1 与 ⊙ O 在 A 处的切线互相垂直，则两切 线分别过另一圆的圆心，如图 D47 所示 . 图 D47 答案： 4 【 规律方法 】 (1) 判断圆与圆的位置关系 利用圆心距与两圆 半径之间的关系； (2) 两圆相切包括内切和外切，两圆相离包括 外离和内含 . 考点 3 直线与圆的综合应用 例 5 ： 已知圆 C ： x 2 ＋ y 2 ＋ x － 6 y ＋ m ＝ 0 和直线 x ＋ 2 y － 3 ＝ 0 相交于 P ， Q 两点，若 OP ⊥ OQ ，求 m 的值 . 思维点拨： 本题主要考查直线的方程、直线与圆的位置 关 系、根与系数的关系等知识 . 则 (0 ＋ 1) 2 ＋ (0 － 2) 2 ＝ r 2 ＝ 5. 在 Rt△ CMQ 中， CM 2 ＋ MQ 2 ＝ CQ 2 ， 方法四，设过 P ， Q 的圆系方程为 x 2 ＋ y 2 ＋ x － 6 y ＋ m ＋ λ ( x ＋ 2 y － 3) ＝ 0. 由 OP ⊥ OQ 知，点 O (0,0) 在圆上 . ∴ m － 3 λ ＝ 0 ，即 m ＝ 3 λ . ∴ 圆的方程化为 x 2 ＋ y 2 ＋ x － 6 y ＋ 3 λ ＋ λx ＋ 2 λy － 3 λ ＝ 0 ， 即 x 2 ＋ (1 ＋ λ ) x ＋ y 2 ＋ 2( λ － 3) y ＝ 0. ∴ λ ＝ 1.∴ m ＝ 3. 【 规律方法 】 求解本题时，应避免去求 P ， Q 两点坐标的 具体数值 . 除此之外，还应对求出的 m 值进行必要的检验，这是 因为在求解过程中并没有确保有交点存在，这一点很容易被大 家忽略 ；方法一显示了解这类题的通法，方法二的关键在于依 需要一定的变形技巧，同时也可以看出，这种方法一气呵成 . 【 跟踪训练 】 2.(2018 年北京 ) 在平面直角坐标系中，记 d 为点 P (cos θ ， sin θ ) 到直线 x － my － 2 ＝ 0 的距离，当 θ ， m 变化时， d 的最大值 为 ( ) A.1 C.3 B.2 D.4 解析： 点 P (cos θ ， sin θ ) 在圆 x 2 ＋ y 2 ＝ 1 上，直线 x － my － 2 ＝ 0 过定点 A (2,0) ，如图 D48 ，圆心到直线 x － my － 2 ＝ 0 的距离 d ≤ OA ，最大值为 2 ， ∴ 圆上任意点到直线 x － my － 2 ＝ 0 的距 离的最大值为 2 ＋ 1 ＝ 3. 图 D48 答案： C 2. 过一点求圆的切线方程的方法 . (1) 过圆上一点 ( x 0 ， y 0 ) 的圆的切线方程的求法 . 先求切点与圆心连线的斜率 k ，由垂直关系知切线斜率为 形写出切线方程 x ＝ x 0 . (2) 过圆外一点 ( x 0 ， y 0 ) 的圆的切线方程的求法 . 设斜率为 k ，切线方程为 y － y 0 ＝ k ( x － x 0 ) ，即 kx － y ＋ y 0 － kx 0 ＝ 0. 由圆心到直线的距离等于半径，即可得出切线方程 . 注意 过圆外一点的圆的切线一定有两条，千万不要遗漏 . 特别当算出 的 k 值只有一个时，结合图形检验，一 定不要忽略斜率不存在 的情况 . 3. 直线与圆相交求弦长的两种方法： (2) 几何法：利用点到直线的距离公式求圆心到直线的距 离，利用勾股定理、垂径定理求弦长 . 4. 圆系方程 . (1) 设两圆 C 1 ： x 2 ＋ y 2 ＋ D 1 x ＋ E 1 y ＋ F 1 ＝ 0 ， C 2 ： x 2 ＋ y 2 ＋ D 2 x ＋ E 2 y ＋ F 2 ＝ 0 ，若两圆相交，则两圆的公共弦所在的直线方程 是 ( D 1 － D 2 ) x ＋ ( E 1 － E 2 ) y ＋ ( F 1 － F 2 ) ＝ 0. (2) 过圆 C ： x 2 ＋ y 2 ＋ Dx ＋ Ey ＋ F ＝ 0 和直线 l ： ax ＋ by ＋ c ＝ 0 的交点的圆系方程为 x 2 ＋ y 2 ＋ Dx ＋ Ey ＋ F ＋ λ ( ax ＋ by ＋ c ) ＝ 0. (3) 过两圆 C 1 ： x 2 ＋ y 2 ＋ D 1 x ＋ E 1 y ＋ F 1 ＝ 0 ， C 2 ： x 2 ＋ y 2 ＋ D 2 x ＋ E 2 y ＋ F 2 ＝ 0 的交点的圆系方程为 x 2 ＋ y 2 ＋ D 1 x ＋ E 1 y ＋ F 1 ＋ λ ( x 2 ＋ y 2 ＋ D 2 x ＋ E 2 y ＋ F 2 ) ＝ 0( 不表示圆 C 2 ).