2013新课标全国卷Ⅰ（理）数学试题 10页

‎2013·新课标全国卷Ⅰ(理科数学)‎ ‎　　　　　　　　　　　　　　　　　　　‎ ‎1． 已知集合A＝{x|x2－2x＞0}，B＝x，则(　　)‎ A．A∩B＝∅ B．A∪B＝‎ C．B⊆A D．A⊆B ‎1．B　[解析] A＝{x|x<0或x>2}，故A∪B＝‎ ‎2． 若复数z满足(3－4i)z＝|4＋3i|，则z的虚部为(　　)‎ A．－4 B．－ C．4 D. ‎2．D　[解析] z＝＝＝＝＋i，故z的虚部是.‎ ‎3． 为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是(　　)‎ A．简单随机抽样 B．按性别分层抽样 C．按学段分层抽样 D．系统抽样 ‎3．C　[解析] 因为总体中所要调查的因素受学段影响较大，而受性别影响不大，故按学段分层抽样．‎ ‎4． 已知双曲线C：－＝1(a＞0，b＞0)的离心率为，则C的渐近线方程为(　　)‎ A．y＝±x B．y＝±x C．y＝±x D．y＝±x ‎4．C　[解析] 离心率＝，所以＝＝＝.由双曲线方程知焦点在x轴上，故渐近线方程为y＝±x.‎ 图1－1‎ ‎5． 执行如图1－1所示的程序框图，如果输入的t∈[－1，3]，则输出的s属于(　　)‎ A．[－3，4]‎ B．[－5，2]‎ C．[－4，3]‎ D．[－2，5]‎ ‎5．A　[解析] 由框图可知，当t∈[－1，1)时，s＝3t，故此时s∈[－3，3)；当t∈[1，3]时，s＝4t－t2＝－(t－2)2＋4，故此时s∈[3，4]，综上，s∈[－3，4]．‎ 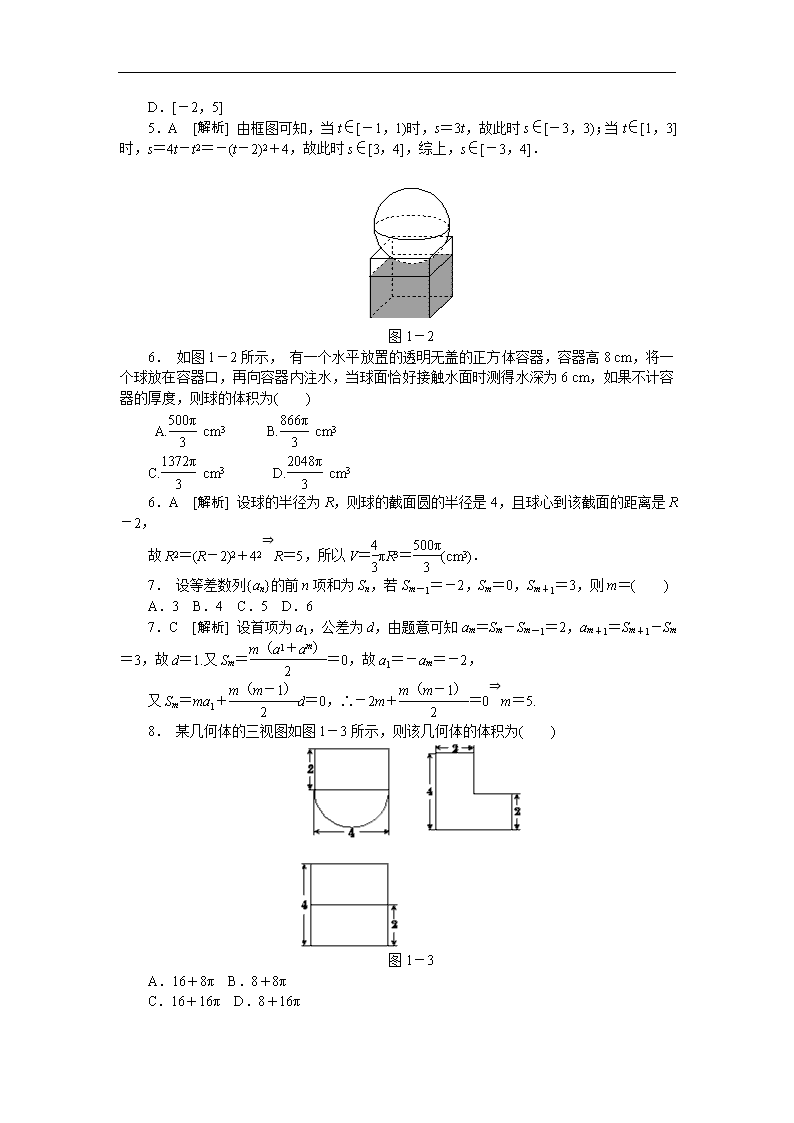图1－2‎ ‎6． 如图1－2所示， 有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为(　　)‎ ‎ A. cm3　　　B. cm3‎ C. cm3 　 　 D. cm3‎ ‎6．A　[解析] 设球的半径为R，则球的截面圆的半径是4，且球心到该截面的距离是R－2，‎ 故R2＝(R－2)2＋42⇒R＝5，所以V＝πR3＝(cm3)．‎ ‎7． 设等差数列{an}的前n项和为Sn，若Sm－1＝－2，Sm＝0，Sm＋1＝3，则m＝(　　)‎ A．3 B．4 C．5 D．6‎ ‎7．C　[解析] 设首项为a1，公差为d，由题意可知am＝Sm－Sm－1＝2，am＋1＝Sm＋1－Sm＝3，故d＝1.又Sm＝＝0，故a1＝－am＝－2，‎ 又Sm＝ma1＋d＝0，∴－2m＋＝0⇒m＝5.‎ ‎8． 某几何体的三视图如图1－3所示，则该几何体的体积为(　　)‎ 图1－3‎ A．16＋8π B．8＋8π C．16＋16π D．8＋16π ‎8．A　[解析] 由三视图可知该组合体下半部分 是一个半圆柱，上半部分是一个长方体，故体积为V＝2×2×4＋×π×22×4＝16＋8π.‎ ‎9． 设m为正整数，(x＋y)2m展开式的二项式系数的最大值为a，(x＋y)2m＋1展开式的二项式系数的最大值为b.若13a＝7b，则 m＝(　　)‎ A．5 B．6 C．7 D．8‎ ‎9．B　[解析] (x＋2y)2m展开式的二项式系数的最大值是C，即a＝C；(x＋2y)2m＋1展开式的二项式系数的最大值是C，即b＝C，∵13a＝7b，∴13C＝7C，∴13＝7，易得m＝6.‎ ‎10． 已知椭圆E：＋＝1(a＞b＞0)的右焦点为F(3，0)，过点F的直线交E于A，B两点，若AB的中点坐标为(1，－1)，则E的方程为(　　)‎ A.＋＝1 B.＋＝1‎ C.＋＝1 D.＋＝1‎ ‎10．D　[解析] 由题意知kAB＝，设A(x1，y1)，B(x2，y2)，则⇒＋＝0.‎ 由AB的中点是(1，－1)知 ‎∴＝＝，联立a2－b2＝9，解得a2＝18，b2＝9，故椭圆E的方程为＋＝1.‎ ‎11．， 已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是(　　)‎ A．(－∞，0] B．(－∞，1]‎ C．[－2，1] D．[－2，0]‎ ‎11．D　[解析] 方法一：若x≤0，|f(x)|＝|－x2＋2x|＝x2－2x，x＝0时，不等式恒成立，x<0时，不等式可变为a≥x－2，而x－2<－2，可得a≥－2；‎ 若x>0，|f(x)|＝|ln(x＋1)|＝ln(x＋1)，由ln(x＋1)≥ax，可得a≤恒成立，‎ 令h(x)＝，则h′(x)＝，再令g(x)＝－ln(x＋1)，则 g′(x)＝<0，故g(x)在(0，＋∞)上单调递减，所以g(x)0，a≤0.综上可知，－2≤a≤0，故选D.‎ 方法二：数形结合：画出函数|f(x)|＝与直线y＝ax的图像，如下图，要使|f(x)|≥ax恒成立，只要使直线y＝ax的斜率最小时与函数y＝x2－2x，x≤0在原点处的切线斜率相等即可，最大时与x轴的斜率相等即可，‎ 因为y′＝2x－2，所以y′|x＝0＝－2，所以－2≤a≤0.‎ ‎12． 设△AnBnCn的三边长分别为an，bn，cn，△AnBnCn的面积为Sn，n＝1，2，3，….若b1＞c1，b1＋c1＝2a1，an＋1＝an，bn＋1＝，cn＋1＝，则(　　)‎ A．{Sn}为递减数列 B．{Sn}为递增数列 C．{S2n－1}为递增数列，{S2n}为递减数列 D．{S2n－1}为递减数列，{S2n}为递增数列 ‎12．B　[解析] 因为an＋1＝an，所以an＝a1.又因为bn＋1＋cn＋1＝(bn＋cn)＋an＝(bn＋cn)＋a1，所以bn＋1＋cn＋1－2a1＝(bn＋cn－2a1)．因为b1＋c1－2a1＝0，所以bn＋cn＝2a1，故△AnBnCn中边BnCn的长度不变，另外两边AnBn，AnCn的和不变．‎ 因为bn＋1－cn＋1＝－(bn－cn)，且b1－c1>0，所以bn－cn＝(b1－c1)，当n→＋∞时，bn→cn，也就是AnCn→AnBn，所以三角形△AnBnCn中BnCn边上的高随着n的增大而增大．设三角形△AnBnCn中BnCn边上的高为hn，则{hn}单调递增，所以Sn＝a1hn是增函数．答案为B.‎ ‎13． 已知两个单位向量，的夹角为60°，＝t＋(1－t)，若＝0，则t＝________．‎ ‎13．2　[解析] 因为||＝||＝1，·＝，所以·＝·[t＋(1－t)]＝t＋1－t＝0，所以t＝2.‎ ‎14． 若数列{an}的前n项和Sn＝an＋，则{an}的通项公式是an＝________．‎ ‎14．(－2)n－1　[解析] 因为Sn＝an＋①，所以Sn－1＝an－1＋②，①－②得an＝an－an－1，即an＝－2an－1，又因为S1＝a1＝a1＋⇒a1＝1，所以数列{an}是以1为首项，－2为公比的等比数列，所以an＝(－2)n－1.‎ ‎15． 设当x＝θ时，函数f(x)＝sin x－2cos x取得最大值，则cos θ＝________．‎ ‎15．－　[解析] 因为f(x)＝sin x－2cos x＝sin(x＋φ)，‎ 所以当x＋φ＝＋2kπ(k∈)，即x＝－φ＋2kπ(k∈)时，y＝f(x)取得最大值，‎ 则cos θ＝cos x＝cos＝sin φ，由φ∈可得 sinφ＝－，所以cosθ＝－.‎ ‎16． 若函数f(x)＝(1－x2)(x2＋ax＋b)的图像关于直线x＝－2对称，则f(x)的最大值为________．‎ ‎16．16　[解析] 方法一：因为f′(x)＝－4x3－3ax2＋2(1－b)x＋a，函数f(x)是连续可导函数，且关于直线x＝－2对称，所以f′(－2)＝0，即f′(－2)＝32－12a－4(1－b)＋a＝0，可得11a－4b＝28，①‎ 又因为f(0)＝f(－4)，所以15a－4b＝60，②‎ ‎①②联立方程组可得a＝8，b＝15，‎ f(x)＝(1－x2)(x2＋8x＋15)，f′(x)＝－4(x3＋6x2＋7x－2)，‎ 因为－2是函数f(x)的一个极值点，所以f′(x)＝－4(x＋2)，‎ 可知当x∈时，f(x)单调递增，当x∈时，f(x)单调递减，当x∈时，f(x)单调递增，当x∈时，f(x)单调递减，且 f＝f，所以f＝f＝f＝＝80－64＝16.‎ 方法二：令f＝0可得x＝1或x＝－1，因为函数f(x)的图像关于直线x＝－2对称，所以，可得以下同方法一．‎ ‎17． 如图1－4所示，在△ABC中，∠ABC＝90°，AB＝，BC＝1，P为△ABC内一点，∠BPC＝90°.‎ ‎(1)若PB＝，求PA；‎ ‎(2)若∠APB＝150°，求tan ∠PBA.‎ 图1－4‎ ‎17．解：(1)由已知得， ∠PBC＝60°，所以∠PBA＝30°.‎ 在△PBA中，由余弦定理得PA2＝3＋－2××cos 30°＝.故PA＝.‎ ‎(2)设∠PBA＝α，由已知得PB＝sin α.‎ 在△PBA中，由正弦定理得＝，化简得cos α＝4sin α.‎ 所以tan α＝，即tan ∠PBA＝.‎ ‎18． 如图1－5所示，三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.‎ ‎(1)证明：AB⊥A1C；‎ ‎(2)若平面ABC⊥平面AA1B1B，AB＝CB，求直线A1C与平面BB1C1C 所成角的正弦值．‎ 图1－5‎ ‎18．解：(1)证明：取AB的中点O，联结OC，OA1，A1B.‎ 因为CA＝CB，所以OC⊥AB.‎ 由于AB＝AA1，∠BAA1＝60°，故△AA1B为等边三角形，所以OA1⊥AB.‎ 因为OC∩OA1＝O，所以AB⊥平面OA1C.‎ 又A1C⊂平面OA1C，故AB⊥A1C.‎ ‎(2)由(1)知OC⊥AB，OA1⊥AB.‎ 又平面ABC⊥平面AA1B1B，交线为AB，所以OC⊥平面AA1B1B，故OA，OA1，OC两两相互垂直．以O为坐标原点，的方向为x轴的正方向，||为单位长，建立如图所示的空间直角坐标系O－xyz.‎ 由题设知A(1，0，0)，A1(0，，0)，C(0，0，)，‎ B(－1，0，0)．‎ 则＝(1，0，)，＝＝(－1，，0)，＝‎ ‎(0，－，)．‎ 设＝(x，y，z)是平面BB1C1C的法向量，‎ 则即 可取＝(，1，－1)．‎ 故cos 〈，〉＝＝－.‎ 所以A1C与平面BB1C1C所成角的正弦值为.‎ ‎19．， 一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n.如果n＝3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n＝4.再从这批产品中任取1件作检验；若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．‎ 假设这批产品的优质品率为50%，即取出的每件产品是优质品的概率都为，且各件产品是否为优质品相互独立．‎ ‎(1)求这批产品通过检验的概率；‎ ‎(2)已知每件产品的检验费用为100元，且抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X(单位：元)，求X的分布列及数学期望．‎ ‎19．解：(1)设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品都是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A＝(A1B1)∪(A2B2)，‎ 且A1B1与 A2B2互斥，所以 P(A)＝P(A1B1)＋P(A2B2)＝P(A1)P(B1|A1)＋P(A2)P(B2|A2)＝×＋×＝.‎ ‎(2)X可能的取值为400，500，800，并且 P(X＝400)＝1－－＝，P(X＝500)＝，‎ P(X＝800)＝.‎ 所以X的分布列为 X ‎400‎ ‎500‎ ‎800‎ P E(X)＝400×＋500×＋800×＝506.25.‎ ‎20．，，， 已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.‎ ‎(1)求C的方程；‎ ‎(2)l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|.‎ ‎20．解：由已知得圆M的圆心为M(－1，0)，半径r1＝1；圆N的圆心为N(1，0)，半径r2＝3.‎ 设圆P的圆心为P(x，y)，半径为R.‎ ‎(1)因为圆P与圆M外切并且与圆N内切，所以 ‎|PM|＋|PN|＝(R＋r1)＋(r2－R)＝r1＋r2＝4.‎ 由椭圆的定义可知，曲线C是以M, N为左、右焦点，长半轴长为2，短半轴长为的椭圆(左顶点除外)，其方程为＋＝1(x≠－2)．‎ ‎(2)对于曲线C上任意一点P(x，y)，由于|PM|－|PN|＝2R－2≤2，所以R≤2，‎ 当且仅当圆P的圆心为(2，0)时，R＝2，所以当圆P的半径最长时，其方程为(x－2)2＋y2＝4.‎ 若l的倾斜角为90°，则l与y轴重合，可得|AB|＝2 .‎ 若l的倾斜角不为90°，由r1≠R知l不平行于x轴，设l与x轴的交点为Q，‎ 则＝，可求得Q(－4，0)，所以可设l：y＝k(x＋4)．由l与圆M相切得＝1，解得k＝±.当k＝时，将y＝x＋代入＋＝1，‎ 并整理得7x2＋8x－8＝0.解得x1，2＝.‎ 所以|AB|＝|x2－x1|＝.‎ 当k＝－时，由图形的对称性可知|AB|＝.‎ 综上，|AB|＝2 或|AB|＝.‎ ‎21． 设函数f(x)＝x2＋ax＋b，g(x)＝ex(cx＋d)．若曲线y＝f(x)和曲线y＝g(x)都过点P(0，2)，且在点P处有相同的切线y＝4x＋2.‎ ‎(1)求a，b，c，d的值；‎ ‎(2)若x≥－2时，f(x)≤kg(x)，求k的取值范围．‎ ‎21．解：(1)由已知得f(0)＝2，g(0)＝2，f′(0)＝4，g′(0)＝4.而f′(x)＝2x＋a，g′(x)＝ex(cx＋d＋c)，故 b＝2，d＝2，a＝4，d＋c＝4.‎ 从而a＝4，b＝2，c＝2，d＝2.‎ ‎(2)由(1)知，f(x)＝x2＋4x＋2，g(x)＝2ex(x＋1)．‎ 设函数F(x)＝kg(x)－f(x)＝2kex(x＋1)－x2－4x－2，则F′(x)＝2kex(x＋2)－2x－4＝2(x＋2)(kex－1)．‎ 由题设可得F(0)≥0，即k≥1.‎ 令F′(x)＝0得x1＝－ln k，x2＝－2.‎ ‎①若1≤k0，即F(x)在(－2，x1)上单调递减，在(x1，＋∞)上单调递增．故F(x)在[－2，＋∞)上的最小值为F(x1)．‎ 而F(x1)＝2x1＋2－x－4x1－2＝－x1(x1＋2)≥0.‎ 故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎②若k＝e2，则F′(x)＝2e2(x＋2)(ex－e－2)．‎ 从而当x>－2时，F′(x)>0，即F(x)在(－2，＋∞)上 单调递增，而F(－2)＝0，故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎③若k>e2，则F(－2)＝－2ke－2＋2＝－2e－2(k－e2)<0，从而当x≥－2时，f(x)≤kg(x)不可能恒成立．‎ 综上，k的取值范围是[1，e2]．‎ 图1－6‎ ‎22． 选修4－1：几何证明选讲如图1－6所示，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.‎ ‎(1)证明：DB＝DC；‎ ‎(2)设圆的半径为1，BC＝，延长CE交AB于点F，求△BCF外接圆的半径．‎ ‎22．解：(1)证明：联结DE，交BC于点G.‎ 由弦切角定理得，∠ABE＝∠BCE.‎ 而∠ABE＝∠CBE，故∠CBE＝∠BCE，BE＝CE.‎ 又因为DB⊥BE，所以DE为直径，∠DCE＝90°，‎ 由勾股定理可得DB＝DC.‎ ‎(2)由(1)知，∠CDE＝∠BDE，DB＝DC，‎ 故DG是BC的中垂线，所以BG＝.‎ 设DE的中点为O，联结BO，则∠BOG＝60°.从而∠ABE＝∠BCE＝∠CBE＝30°，‎ 所以CF⊥BF，故Rt△BCF外接圆的半径等于.‎ ‎23． 选修4－4：坐标系与参数方程 已知曲线C1的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.‎ ‎(1)把C1的参数方程化为极坐标方程；‎ ‎(2)求C1与C2交点的极坐标(ρ≥0，0≤θ＜2π)．‎ ‎23．解：(1)将消去参数t，化为普通方程(x－4)2＋(y－5)2＝25，‎ 即C1：x2＋y2－8x－10y＋16＝0.‎ 将代入x2＋y2－8x－10y＋16＝0，得ρ2－8ρcos θ－10ρsin θ＋16＝0.‎ 所以C1的极坐标方程为ρ2－8ρcos θ－10ρsin θ＋16＝0.‎ ‎(2)C2的普通方程为x2＋y2－2y＝0，‎ 由解得或 所以C1与C2交点的极坐标分别为，.‎ ‎24． 选修4－5：不等式选讲 已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)＝x＋3.‎ ‎(1)当a＝－2时，求不等式f(x)＜g(x)的解集；‎ ‎(2)设a＞－1，且当x∈时，f(x)≤g(x)，求a的取值范围．‎ ‎24．解：(1)当a＝－2时，不等式f(x)