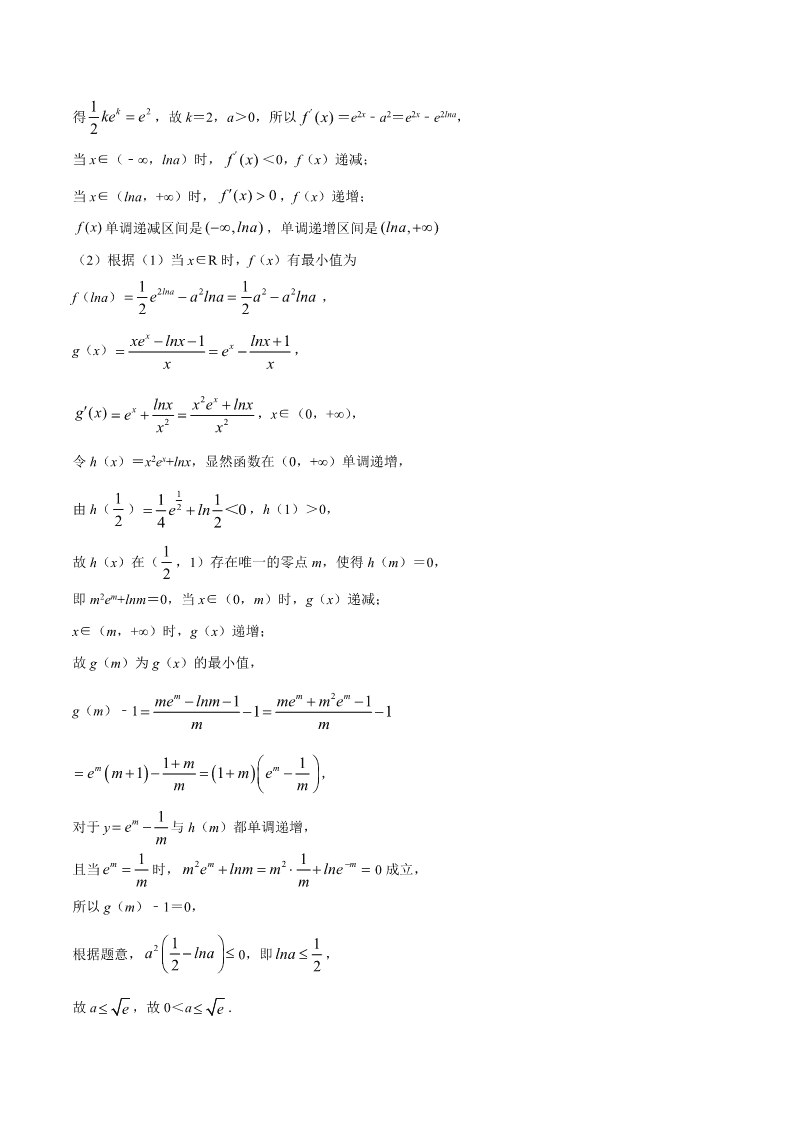高考数学复习专题-导函数解答题学霸必刷35题A卷（教师版） 52页

导函数解答题学霸必刷 35 题 A 卷 1．已知函数 21 3( ) ln 2 2 2 f x x ax x    ( 0)a  . （1）讨论函数 ( )f x 的极值点的个数； （2）若 ( )f x 有两个极值点 1,x 2x ，证明：    1 2 0f x f x  . 【答案】（1）答案不唯一，具体见解析；（2）证明见解析. 【解析】 （1） 1( ) 2f x ax x     2 2 1,ax x x    (0, )x  . ①当 0a  时， 2 1( ) xf x x    . 当 10, 2 x      时， ( ) 0f x  ，所以 ( )f x 在 10, 2       上单调递增； 当 1 , 2 x       时， ( ) 0f x  ，所以 ( )f x 在 1 , 2      上单调递减. 即函数 ( )f x 只有一个极大值点 1 2 ，无极小值点. ②当0 1a  时， 4 4 0a    ， 令 ( ) 0f x  ，得 1 1 ax a    . 当 1 1 1 10, ,a ax a a                     时， ( ) 0f x  ， 所以 ( )f x 在 1 10, ,a a         1 1 ,a a         上单调递增； 当 1 1 1 1,a ax a a           时， ( ) 0f x  ， 所以 ( )f x 在 1 1 1 1,a a a a           上单调递减. 即函数 ( )f x 有一个极大值点 1 1 a a   ，有一个极小值点 1 1 a a   . ③当 1a  时， 4 4 0a    ，此时 ( ) 0f x  恒成立， 即 ( )f x 在 (0, ) 上单调递增，无极值点. 综上所述，当 0a  时， ( )f x 有且仅有一个极大值点，即只有 1个极值点； 当0 1a  时， ( )f x 有一个极大值点和一个极小值点，即有 2个极值点； 当 1a  时， ( )f x 没有极值点. （2）由（1）可知，当且仅当0 1a  时， ( )f x 有两个极值点 1,x 2x ，且 1,x 2x 为方程 2 2 1 0ax x   的两根， 即 1 2 2 ,x x a   1 2 1x x a  ， 所以        2 2 1 2 1 2 1 2 1 2ln 2 3 2 af x f x x x x x x x       2 1 4 2 4ln 3 2 a a a a a          2ln 2a a     . 令 2( ) ln 2,g a a a     (0,1)a ， 则 2 2 1 2 2( ) 0ag a a a a       恒成立， 所以 ( )g a 在 (0,1)上单调递增， 所以 ( ) (1) ln1 2 2 0g a g      ， 即    1 2 0f x f x  . 2．已知函数 f（x） 1 2 kxe  a2x（k∈R，a＞0，e为自然对数的底数），且曲线 f（x）在点（1，f（1））处 的切线的斜率为 e2﹣a2． （1）求实数 k的值，并讨论函数 f（x）的单调性； （2）设函数 g（x） 1xxe lnx x    ，若对∀x1∈（0，+∞），∃x2∈R，使不等式 f（x2）≤g（x1）﹣1成立， 求实数 a的取值范围． 【答案】（1）k＝2，见解析（2）0＜a e ． 【解析】 （1） 21 2 ( ) kxef x k a  ，f'（1） 2 2 21 2 kke a e a    ， 得 21 2 kke e ，故 k＝2，a＞0，所以 ( )f x ＝e2x﹣a2＝e2x﹣e2lna， 当 x∈（﹣∞，lna）时， ( )f x ＜0，f（x）递减； 当 x∈（lna，+∞）时， ( ) 0f x  ，f（x）递增； ( )f x 单调递减区间是 ( , )lna ，单调递增区间是 ( , )lna  （2）根据（1）当 x∈R时，f（x）有最小值为 f（lna） 2 2 2 21 1 2 2 lnae a lna a a lna    ， g（x） 1 1x xxe lnx lnxe x x       ， ( )g x 2 2 2 x x lnx x e lnxe x x     ，x∈（0，+∞）， 令 h（x）＝x2ex+lnx，显然函数在（0，+∞）单调递增， 由 h（ 1 2 ） 1 21 1 0 4 2 e ln  ＜ ，h（1）＞0， 故 h（x）在（ 1 2 ，1）存在唯一的零点 m，使得 h（m）＝0， 即 m2em+lnm＝0，当 x∈（0，m）时，g（x）递减； x∈（m，+∞）时，g（x）递增； 故 g（m）为 g（x）的最小值， g（m）﹣1 21 11 1 m m mme lnm me m e m m            1 11 1m mme m m e m m            ， 对于 y 1me m   与 h（m）都单调递增， 且当 1me m  时， 2 2 1m mm e lnm m lne m      0成立， 所以 g（m）﹣1＝0， 根据题意， 2 1 2 a lna      0，即 1 2 lna  ， 故 a e ，故 0＜a e ． 3．已知函数 ( ) ( ) lnxf x a x a   ( 0)a  . （1）若函数 ( )f x 在[1, ) 上是增函数，求正数a的取值范围； （2）当 1a  时，设函数 ( )f x 的图象与 x轴的交点为 A， B，曲线 ( )y f x 在 A， B两点处的切线斜率 分别为 1k ， 2k ，求证： 1k + 2k 0 . 【答案】（1） (0,1]； （2）见解析. 【解析】 （1）   lnxf x a x a       ( 0)a  ，∴   2lnx x x af x ax    ， 设   2lng x x x x a   ， 函数  f x 在  1, 上是增函数，∴   2lng x x x x a   0 在 1, 上恒成立，即 2 lna x x x  在  1, 上恒成立， 设   lnh x x x x  ，则   ln 2h x x  ， 1x  ，∴   2h x  ，∴   lnh x x x x  在 1, 上是增函数， ∴   1h x  ，由 2 lna x x x  在 1, 上恒成立，得 2 1a  ， 0a  ， ∴0 1a  ，即 a的取值范围是  0,1 . （2） 1a  ，由   ln 0xf x a x a        ，得 1 1x  ， 2 2x a ，不妨设    21,0 , ,0A B a .    2lnx x x af x ax    ， 2 1 1 ak a    ， 2 2 lnak a  ， 1k + 2k 2 2ln 1a a a    ， 设   ln 1F x x x   ，则   1 xF x x    ， 0 1x   时，   0F x  ， 1x  时，   0F x  ，所以 1x  为   ln 1F x x x   的极大值点，所以   ln 1F x x x   的极大值即最大值为  1 0F  ，即   ln 1 0F x x x    ， ∵ 0a  且 1a  ，∴ 2 0a  且 2 1a  ， ∴  2 2 2ln 1 0F a a a    ，∴ 1k + 2k 2 2ln 1a a a    0 . 4．已知函数    22 ln 2 1 8x mxx xf m     ，m R . （1）讨论函数  f x 的单调性； （2）对实数 2m  ，令     3g x f x x  ，正实数 1x ， 2x 满足    1 2 1 22 0g x g x x x   ，求 1 2x x 的 最小值. 【答案】（1）见解析（2）6 【解析】 （1）         2 1 12 2 2 1' 0 x f x mx mx m x x x         . 若 0m  ，当  0,1x 时，  ' 0f x  ，即  f x 在  0,1 上单调递增； 当  1,x  时，  ' 0f x  ，即  f x 在  1, 上单调递减. 若0 1m  ，当   10,1 ,x m        时，  ' 0f x  ，即  f x 在（  0,1 ， 1 , m      上均单调递增； 当 11,x m      时，  ' 0f x  ，即  f x 在 11, m       上单调递减. 若 1m  ，则  ' 0f x  ，即  f x 在  0,  上单调递增. 若 1m > ，当  10, 1,x m        时，  ' 0f x  ，即  f x 在 10, m       ，  1, 上均单调递增； 当 1 ,1x m      时，  ' 0f x  ，即  f x 在 1 ,1 m       上单调递减. （2）当实数 2m  时，      23 2ln 2 9 8 0g x f x x x x x x       ，    1 2 1 22 0g x g x x x   ， 2 2 1 1 1 2 2 2 1 22ln 2 9 8 2ln 2 9 8 2 0x x x x x x x x          ，      2 1 2 1 2 1 2 1 22 9 16 2 2lnx x x x x x x x       ， 令 1 2t x x ，    2 2ln 0h t t t t   ， 由于    2 1 ' t h t t   ，知当  0,1t 时，  ' 0h t  ，即  h t 单调递减； 当  1,t  时，  ' 0h t  ，即  h t 单调递增. 从而，    min 1 2h t h  ， 于是，    2 1 2 1 22 9 16 2x x x x     ，即    1 2 1 22 3 6 0x x x x       ， 而 1 2, 0x x  ，所以 1 2 6x x  ， 而当 1 3 2 2x   ， 2 3 2 2x   时， 1 2x x 取最小值 6. 5．已知函数   21ln 2 f x x x ax x   恰有两个极值点  1 2 1 2,x x x x . (1)求实数 a的取值范围； (2)求证： 2 2 12 1 a x        ； (3)求证： 1 2 1 1 2 ln ln ae x x   （其中 e为自然对数的底数）. 【答案】(1) 1(0, ) e ；(2)证明见解析；(3)证明见解析. 【解析】 (1)由题意得   lnf x x ax   ，故 ln xa x  ， 设    ln 0xg x x x   ，   2 1 ln xg x x   ， 故0 x e  时，   0,g x x e   时，   0g x  ， 故  g x 在  0,e 递增，在 ( , )e  递减， 又     11 0,g g e e   ， 当 x e 时，   0g x  ， 故实数a的范围是 1(0, ) e ； (2)由(1)得 2 2ln 0x ax  ，且 2x e ，故 2 2 ln xa x  ， 要证明 2 2 ( )12 1 a x   ，只要证明 2 2 2 2 1 ln2 1 x x x        ， 只要证明 2 2 2 ( )12 lnx x x   ， 设    22 ln ,h x x x x e x     ， 则 2 (2 1) 2( ) 0x xh x x     ， 故  h x 在 ( , )e  递增， 故     22 1 0h x h e e e      ， 故 2 2 ( )12 1 a x   成立； (3)由(1)得 1 1 2 2ln 0,ln 0x ax x ax    ， 且 1 21 x e x   ，故 1 2 1 2 ln lnx xa x x    ， 由(1)得0 1ae  ，要证明 1 2 1 1 2 ln ln ae x x   ， 只需证明 1 2 1 1 2 ax ax   ， 只需证明 1 2 1 1 2a x x   ， 故 1 2 1 1 2a x x   1 2 1 2 1 2 1 2 ln ln2x x x x x x x x       1 2 1 1 2 2 1 2 1 2lnx x x x x x x x         ， 设    1 2ln 0 1G x x x x x      ， 则 2 2 ( 1)( ) 0xG x x    ， 故  G x 在  0,1 递增， 结合 1 2 0 0x x   ，故 1 2 0x x  ， 1 2 1 2 1 2 2ln 0x x x x x x    ，有 1 2 1 1 2 0a x x    ， 故 1 2 1 1 2 ax ax   ， 故 1 2 1 1 2 ln ln ae x x   . 6．已知函数 ( ) 2 ln , (1) 0bf x ax x f x     （Ⅰ）若函数 ( )f x 在其定义域上为单调函数,求a的取值范围； （Ⅱ）若函数 ( )f x 的图像在 1x  处的切线的斜率为 0， 2 1 1( ) 1 1n n a f n a n      ，已知 1 4,a  求证： 2 2na n  （Ⅲ）在（2）的条件下，试比较 1 2 3 1 1 1 1 1 1 1 1 na a a a          与 2 5 的大小，并说明理由. 【答案】（Ⅰ）    ,0 1,   ；（Ⅱ）略；（Ⅲ） 1 2 3 1 1 1 1 1 1 1 1 na a a a          < 2 5 . 【解析】 (Ⅰ) ∵f(1)="a-b=0" ∴a=b ∴ ( ) 2 lnaf x ax x x    ∴ 2 2 2 2 2( ) a ax x af x a x x x        要使函数 ( )f x 在其定义域上为单调函数，则在定义域（0，+∞）内 ( )f x 恒大于等于 0或恒小于等于 0， 当 a=0时， 2( ) 0f x x    在（0，+∞）内恒成立； 当 a>0时， 2 2 2( ) 0ax x af x x     恒成立，则 24 4 0a    ∴ 1a  当 a<0时， 2 2 2( ) 0ax x af x x     恒成立 ∴a的取值范围是:    ,0 1,   (Ⅱ) (1) 2 0f a a    ∴a=1 则： 21( ) ( 1)f x x   于是 2 2 2 2 1 1( ) 1 ( ) 1 2 1 1n n n n n a f n a n n a na a n             用数学归纳法证明 2 2na n  如下： 当 n=1时， 1 4 2 1 2a     ，不等式成立； 假设当 n=k时，不等式 2 2ka k  成立，即 2 2na k  也成立， 当 n=k+1时， 1 ( 2 ) 1 (2 2) 2 1 4 5 2( 1) 2k k ka a a k k k k             所以当 n=k+1时不等式成立， 综上得对所有 n N 时，都有 2 2na n  （Ⅲ）由（2）得 2 1 1 1 12( 1) 1 ( 2 2) 1n n n n na a n a a a n            1 12( 1) 2 2 2 1 2 1n na n n a         于是 11 2( 1)( 2)nna a n    所以 2 11 2( 1),a a   3 21 2( 1),a a   ， 11 2( 1),n na a    累乘得： 1 11 2 ( 1),n na a   则 1 1 1 1 1 ( 2) 1 2 1n n n a a     所以 2 1 1 2 1 1 1 1 1 1 1 1(1 ) 1 1 1 1 2 2 2nna a a a             2 1 2(1 ) 5 2 5n   7．已知函数    2 1 e xf x x ax   . （1）讨论  f x 的单调性； （2）若函数    2 1 e 1xg x x mx    在 1,  有两个零点，求 m的取值范围. 【答案】（1）答案不唯一，具体见解析（2） 21 1 e m „ 【解析】 解：（1）因为    2 1 xf x x ax e   ，所以    2 2 1 exf x x a x a       ， 即      1 1 e xf x a xx     . 由   0f x  ，得  1 1x a   ， 2 1x   . ①当 0a  时，    21 e 0xf xx   … ，当且仅当 1x   时，等号成立. 故  f x 在  ,  为增函数. ②当 0a  时，  1 1a    ， 由   0f x ′ 得  1x a   或 1x   ，由   0f x ′ 得  1 1a x     ； 所以  f x 在   , 1a   ，  1,  为增函数，在   1 , 1a   为减函数. ③当 0a  时，  1 1a    ， 由   0f x ′ 得  1x a   或 1x   ，由   0f x ′ 得  1 1x a     ； 所以  f x 在  , 1  ，   1 ,a   为增函数，在   1, 1a   为减函数. 综上，当 0a  时，  f x 在为  ,  增函数； 当 0a  时，  f x 在   , 1a   ，  1,  为增函数，在   1 , 1a   为减函数； 当 0a  时，  f x 在  , 1  ，   1 ,a   为增函数，在   1, 1a   为减函数. （2）因为    2 1 e 1xg x x mx    ，所以    21 e xg x mx    ， ①当 0m„ 时，   0g x … ，  g x 在 1,  为增函数，所以  g x 在 1,  至多一个零点. ②当 0m  时，由（1）得  g x 在 1,  为增函数. 因为  0 1g m   ，  0 0g  . （ⅰ）当 1m  时，  0 0g  ， 0x  时，   0g x  ， 1 0x   时，   0g x  ； 所以  g x 在 1,0 为减函数，在  0, 为增函数，    min 0 0g x g  . 故  g x 在 1,  有且只有一个零点. （ⅱ）当 1m > 时，  0 0g  ，    21 0mg m e mm     ，  0 0,x m  ，使得  0 0g x  ， 且  g x 在 01, x 为减函数，在  0 ,x  为增函数. 所以    0 0 0g x g  ，又      2 2 2 21 e 1 1 1 0mg m m m m m         ， 根据零点存在性定理，  g x 在  0 ,x m 有且只有一个零点. 又  g x 在 01, x 上有且只有一个零点 0. 故当 1m > 时，  g x 在 1,  有两个零点. （ⅲ）当0 1m  时，   01g m    ，  0 0g  ，  0 1,0x   ，使得  0 0g x  ， 且  g x 在 01, x 为减函数，在  0 ,x  为增函数. 因为  g x 在  0 ,x  有且只有一个零点 0， 若  g x 在 1,  有两个零点，则  g x 在 01, x 有且只有一个零点. 又    0 0 0g x g  ，所以  1 0g  … 即   21 1 0 e g m    … ，所以 21 e m … ， 即当 21 1 e m „ 时  g x 在 1,  有两个零点. 综上，m的取值范围为 21 1 e m „ 8．已知函数   1 1 f x a x    （aR ）. （1）若 2a  ，证明：当 1x  时，  2 ln x f x ； （2）若对于任意的 0x  且 1x  ，都有   2 ln 1a f x x   ，求 a的取值集合. 【答案】(1)证明见解析；(2) 1 2       . 【解析】 （1）当 2a  时，   1 2 1 f x x    ， 要证当 1x  时，  2 ln x f x ， 即证当 1x  时， 12ln 2 1 x x    令   12 ln 1 g x x x    ，            2 2 2 2 2 1 22 1 2 5 2 1 1 1 x xx xg x x x x x x x           当1 2x  时，   0g x  ，  g x 在  1, 2 内单调递减 当 2x  时，   0g x  ，  g x 在  2, 内单调递增， 故    min 2 2ln 2 1 ln 4 1 ln 1 2g x g e        .证毕. (2)先分析端值，当 0x  时， ln x， 1 1 1 a a x      ， 要使 1 ln 1 1 a x x      ，需有 1 0a   ，即 1a  ； 当 x时， ln x， 1 1 a a x    ， 要使 1 ln 1 1 a x x      ，需有 0a  ； 故必须有0 1a  . 由  1 11 1 1 a x a x x       知其分子恒正， 令     1ln 1 1 xx x a x       ， 于是问题等价于当 1x  时，   0x  ； 当0 1x  时，   0x  . 注意到  1 0  .         22 2 1 1 ' 1 a x a x x x ax a           ①当 0a  时   1' xx x     ， 此时当 1x  时，  ' 0x  ，  x 在  1, 单调递减， 于是    1 0x   ，这不符合题意； ②当 0a  时，  ' 0x  ，得 2 1 1 1x a       ， 2 1x  . （i）当 1 2 a  时， 1 2x x ，  ' 0x  ，  x 在  0,  单调递增， 结合  1 0  可知符合题意； （ii）当 10 2 a  时， 1 2x x ，此时当 211, 1x a          时  ' 0x  ， 于是在  x 在 211, 1 a         单调递减， 故在 211, 1 a         内    1 0x   ，这不符合题意； （iii）当 1 2 a  时， 1 2x x ，此时当 21 1 ,1x a          时  ' 0x  ， 于是在  x 在 21 1 ,1 a         单调递减， 故在 21 1 ,1 a         内    1 0x   ，这不符合题意； 综上：符合题意的 a取值集合为 1 2       . 9．已知   1 2 1x xf x ae a    . （1） 1a  时，求  f x 的单调区间和最值； （2）①若对于任意的  0,x  ，不等式    21 2 x f x   恒成立，求a的取值范围；②求证： 1 32 ln 0 2 xe x x     【答案】（1）减区间为  0,1 ，增区间为  1, ，最小值为 0，无最大值；（2）① 1, ；②证明见解析. 【解析】 （1）当 1a  时，   1 2 1xf x e x   ，则   1 1xf x e x   ， 易知  y f x  单调递增，又  1 0f   ，当 0 1x  时，   0f x  ，当 1x  时，   0f x  . 所以，函数  y f x 的减区间为  0,1 ，增区间为  1, ， 函数  y f x 的最小值为  1 0f  ，无最大值； （2）①必要性：若 0a  ，则当 x时，  f x ，不合乎题意，所以，必有 0a  . 又   22 21 0 1 0a af a a a         ，则  1,a  ； 充分性：易知   1 2 1xf x e x   . 故只要证明  21 1 2 1 2 x x e x     在  0,x  恒成立即可， 即  21 1 1 2 0 2 xx e x e             ，令    21 1 1 2 2 xx g x e x e             ， 则     3 2 21 3 2 2 xeg x x x x x x x                    2 1 1 1 2 2 2 xex x x x x x            ， 则  y g x 在  0,1 单调递减，在  1, 单调递增，则    1 0g x g  . 故  1,a  ，因此，实数 a的取值范围是 1, ； ②由①可知，要证 1 32 ln 0 2 xe x x     ，只需证  21 1ln 0 2 2 x x     ， 先证明不等式 1 lnx x  ，构造函数   1 lnh x x x   ， 0x  ，   1 11 xh x x x      ，令   0h x  ，可得 1x  . 当0 1x  时，   0h x  ；当 1x  时，   0h x  . 所以，函数  y h x 的减区间为  0,1 ，增区间为  1, ，    1 0h x h   ， 所以，对任意的 0x  ， 1 lnx x  .        2 2 221 1 21 1 4 4ln 1 0 2 2 2 2 2 2 x x xx xx x               ， 故 1 32 ln 0 2 xe x x     成立. 10．已知， ( ) ( 2) xf x x e  . （1）当 0a… 时，求 21( ) 2 ( ) ( 1) 2 g x f x a x   的单调区间； （2）若当 0a… 时，不等式  21( ) 2 4 2 f x a x x  … 在[0, ) 上恒成立，求实数 a的取值范围. 【答案】（1）增区间为 (1, ) ，减区间为 ( ,1) （2） 1 2 a  【解析】 （1）由题意知： 2 21( ) (2 4) ( 1) 2 g x x x a x    . 所以 ( ) (2 2) ( 1)xg x x e a x     . 即  ( ) ( 1) 2 xg x x e a    因为 0a… ，令 ( ) 0g x  ，得 1x  ， 令 ( ) 0g x  ，得 1x  ， 所以  g x 在 (1, ) 上单调递增， 在 ( ,1) 上单调递减. （2）设  2( ) ( ) 2 4 2 ah x f x x x    . 因为 ( ) ( 1) ( 2)xh x x e a x     . 令 ( ) ( ) ( ) ( 1) ( 2)xm x h x h x x e a x       . 有 ( ) xm x xe a   .因为 0a… ，有 ( ) 0m x … ， 此时函数 ( )y m x 在[0, ) 上单调递增， 则 ( ) (0) 2 1m x m a … . （ⅰ）若 2 1 0a   即 1 2 a  时， ( )y h x 在[0, ) 上单调递增， 则 min( ) (0) 0h x h  恒成立； （ⅱ）若 2 1 0a   即 10 2 a „ 时， 则在[0, ) 存在  0 0h x  . 此时函数 ( )y h x 在 0(0, )x 上单调递减，  0 ,x x  上单调递增且 (0) 0h  ， 所以不等式不可能恒成立，故不符合题意； 综上所述：  21( ) 2 4 2 f x a x x  … 在[0, ) 恒成立， 实数 a的取值范围为 1 2 a  . 11．若函数 ( ) ( )x xf x e ae mx m R    为奇函数，且 0x x 时 ( )f x 有极小值  0f x . （1）求实数 a的值； （2）求实数m的取值范围； （3）若  0 2f x e   恒成立，求实数m的取值范围. 【答案】（1）1；（2） (2, ) ；（3） 12,e e     【解析】 （1）由函数 ( )f x 为奇函数可得 (0) (0)f f  ，则 (0) 0f  ，1 0 0a m    ，则 1a  ， 此时 ( ) x xf x e e mx   ，对任意 xR ， ( ) ( )x xf x e e mx f x      ， 满足 ( )f x 为奇函数， 1a  ； （2） ( ) x xf x e e m    ， ① 2m  时，由 0xe  ，可得 2 2x x x xe e e e     ，则 ( ) 0f x  ，仅当 0x  时可能为 0， 则 ( )f x 在 R上单调递增，无极小值； ② 2m  时， 2 4 0m   ，令 ( ) 0f x  ，可得  2 1 0x xe me   ，则 2 4 2 x m me    ， 2 2 4 2 0 2 4 m m m m       ， 2 4 0 2 m m   ， 即 2 1 4ln 2 m mx    ， 2 2 4ln 2 m mx    ，则 ( ) 0f x  的解为 1 2 1 2, ,x x x x ， ( )f x 单调性如下表： x  1, x  1 2,x x  2 ,x  ( )f x + - + ( )f x 递增 递减 递增 则 ( )f x 在 2x x 处取得极小值，即 0 2x x ，满足题意； 综上，m的取值范围是 (2, ) ； （3）根据第二问可得 0 0 2 0 4 2 0, ln ln 0 2 2 x x m me e m x         ， 则        0 0 0 0 0 0 0 0 0 0 0 01 1x x x x x x xf x e e mx e x e e x e x e            ， 令 ( ) (1 ) (1 )x xp x x e x e    ，  2( ) 1x x x xp x xe xe xe e       ， 则 0x  时 ( ) 0, ( )p x p x  单调递减， 由 2(1)p e   ，  0 2p x e   ， 0 0x  ，可得 0 (0,1]x  ， 令 0xt e ，则 (1, ]t e ， 1m t t   在 (1, ]e 单调递增，则m的取值范围是 12,e e     . 12．已知函数 ( ) 1,f x xlnx ax a R    （1）当 0x  时，若关于 x的不等式 ( ) 0f x  恒成立，求 a的取值范围； （2）当 *n N 时，证明： 2 2 23 12 2 4 2 1 n n nln ln ln n n n          ． 【答案】（1）[ 1, )  .（2）见解析. 【解析】 （1）由   0f x  ，得 ln 1 0x x ax   ( 0)x  . 整理，得 1lna x x    恒成立，即 min 1lna x x        . 令   1lnF x x x   .则   2 2 1 1 1' xF x x x x     . ∴函数  F x 在  0,1 上单调递减，在  1, 上单调递增. ∴函数   1lnF x x x   的最小值为  1 1F  . ∴ 1a  ，即 1a   . ∴a的取值范围是  1,  . （2）∵ 2 4 n n  为数列     1 1 2n n          的前 n项和， 1 n n  为数列   1 1n n         的前 n项和. ∴只需证明    21 1ln 1 2 n n n n       1 1n n   即可. 由（1），当 1a   时，有 ln 1 0x x x   ，即 1lnx x x   . 令 1 1nx n    ，即得 1ln 1 1 n n n n     1 1n   . ∴ 2 2 1 1ln 1 n n n          1 1 2n n    1 1 1 2n n     . 现证明   2 1 1ln 1 n n n n    ， 即 1 12ln 1 n n n n    1 1 n n n n     1 1 n n n n     .  * 现证明 12ln ( 1)x x x x    . 构造函数   1 2lnG x x x x     1x  ， 则   2 1 2' 1G x x x    2 2 2 1 0x x x     . ∴函数  G x 在  1,  上是增函数，即    1 0G x G  . ∴当 1x  时，有   0G x  ，即 12lnx x x   成立. 令 1nx n   ，则  * 式成立. 综上，得    21 1ln 1 2 n n n n       1 1n n   . 对数列     1 1 2n n          ， 2 1ln n n       ，   1 1n n         分别求前 n项和，得 2 2 3ln 2 ln 2 4 2 n n    2 1ln 1 n n n n      . 13．已知函数      ln 0f x ax b x a    . （1）当 0a b  时，试讨论函数  f x 的单调性，并求出函数  f x 的极值； （2）若   3f x x 恒成立，求 2a b的最大值. 【答案】（1）①当 0a  时，  f x 在  1, 上单调递增，  f x 无极值，②当 0a  时，  f x 在  ,0 上单调递增，在  0,1 上单调递减，  f x 的极大值  ln a ，  f x 无极小值（2） 24 3 e 【解析】 （1）    ln 1f x a x x     ①当 0a  时，  f x 的定义域为  1, ，   0 1 xf x x     ，  f x 在  1, 上单调递增，且  f x 无极值 ②当 0a  时，  f x 的定义域为  ,1 ，   1 xf x x    ，  f x 在  ,0 上单调递增，在  0,1 上单调递减， 当 0x  时，  f x 取得极大值  ln a ，且  f x 无极小值 （2）  ln 2ax b x  ，    ln 2g x ax b x   . 若 0a  ，由 0ax b  知 bx a   ，取 0 bx a   ，使得  0 2ln 1bax b a     ， 则  0 0 2 1 2bg x x a     ，而 2 1 0 b aax b e    ， 2 1 0 b ae b bx a a       所以 0 22 bx a   ，所以  0 2 21 1 0b bg x a a       ，与  0 0g x  矛盾 故 0a  ，且   22 2 2 2 a ba x ax a b ag x ax b ax b             ， 故  g x 在 2, 2 b a b a a      上单调递增，在 2 , 2 a b a      上单调递减， 因此  min 2 2ln 0 2 2 2 a b a a bg x g a a          ，故 ln 2 2 aa a b   所以 3 3 2 ln 2 2 aa a a b   记   3 3 ln 2 2 aa a M a   ，则   23 2ln 2 2 3 a aM a         ，则  M a 在 2 30,2e       上单调递增，在 2 32 ,e       上单调递减，因此   2 23 max 42 3 M a M e e        ， 所以当 2 32a e ， 2 31 3 b e 时， 2a b取得最大值 24 3 e . 14．已知函数   2ln 2f x x x ax ax a     . （1）当 1 2 a  时，判断  f x 在定义域上的单调性； （2）若对定义域上的任意的  1,x  ，有   1f x ≤ 恒成立，求实数 a的取值范围； （3）证明： 1 1 1 ln 2 1 2 1 n i n i     ，  *n N . 【答案】（1）因为   12 0f x x x          所以  f x 在  0,  上单调递减，（2） 1 2 a  ，（3）证明见解 析. 【解析】 （1）当 1 2 a  时,   21 1ln 2 2 f x x x x x     ,故   12f x x x         因为 1 12 2x x x x     ,当且仅当 1x  时取等号.故   12 0f x x x          所以  f x 在  0,  上单调递减. （2）∵     1 2 1ax x f x x    , 当 0a  时,则   0f x  ,∴  f x 在 1, 上单调递增,    1 1f x f  , 当 10 2 a  时,令   0f x  ,解得 1 2 x a  , 当 11 2 x a   时,   0f x  ,当 1 2 x a  时,   0f x  , ∴  f x 在 11, 2a      上单调递增,在 1 2 , a     上单调递减,则 11, 2 x a     时,    1 1f x f  , 当 1 2 a  时,   0f x  ,  f x 在 1, 上单调递减,则    1 1f x f  , ∴ 1 2 a  （3）当 1n  时,1 1 ln 3  成立 当 2n  时,由（2）知,    211 ln 1 2 x x x    对任意 1x  都成立 取 2 1 2 1 ix i    , *i N ,则 22 1 2 1 1 2 11 ln 1 2 1 2 1 2 2 1 i i i i i i                  所以  2 2 2 1 2ln 2 1 2 1 2 1 i i i i       当 2i  时          2 2 2 2 1 1 2 1 2 1 2 1 2 3 2 3 2 12 1 i i i i i ii           所以 2 2 2 2 1 1 1ln 2 1 2 1 2 3 2 1 n n i i i i i i i                   所以 2 2 2 1 1 1ln 2 1 3 1 2 1 n i n i n          所以     1 2 12 ln 2 1 ln3 1 2 ln 2 1 2 1 2 1 n i n n i n                所以 1 2 1 ln 2 1 2 1 n i n i     15．设m为实数，已知函数 ( ) x x mf x e   的导函数为 ( )f x ，且 (0) 0f   . （1）求m的值； （2）设 a为实数，若对于任意 xR ，不等式 2 ( )x a f x  恒成立，且存在唯一的实数 0x 使得 2 0 0( )x a f x  成立，求 a的值； （3）是否存在负数 k，使得 3y kx e   是曲线 ( )y f x 的切线.若存在，求出 k的所有值：若不存在，请说 明理由. 【答案】（1） 1m  （2） 1a  （3） 1 e  【解析】 （1）因为 1 ( )( ) x x mf x e     ， 所以 0 1 (0 )(0) 1 0mf m e        ， 故 1m  . （2）因为 2, ( )x R x a f x    ， 所以 2 1 0x xx a e     恒成立. 记 2 1( ) x xx x a e      ， 则 1( ) 2 2x x xx x x e e           ， 因为 xR ，且 0xe  ， 所以 12 0xe   ， 因此为 0x  时， ( ) 0x  ， ( )x 单调递减； 当 0x  时， ( ) 0x  ， ( )x 单调递增， 所以 ( ) (0) 1 0minx a     ，即 1a  ， 当 1a  时， 2( ) ( ) 1 0x x a f x a       ， 故方程 2 ( )x a f x  无解， 当 1a  时，当 0x  时，由单调性知 2( ) ( ) 0x x a f x     所以存在唯一的 0 0x  使得 2 0 0( )x a f x  ，即 1a  . （3）设切点的横坐标为 t，则 ( ) 3 1 t k f t tkt e e       ，即 3 1 t t tk e tkt e e         ， 23 1 t t t t e e e    ，即 23 1(*)t t t e e    原命题等价于存在正数 t使得方程 (*)成立. 记 2 1( ) t t tg t e    ， 则  2(2 1) 1 ( 1)( ) t t t t t t tg t e e          ， 令 ( ) 0g t  ，则 1t  ， 因此当0 1t  时， ( ) 0g t  ， ( )g t 单调递增， 3( ) (1)g t g e   ； 当 1t  时， ( ) 0g t  ， ( )g t 单调递减， 3( ) (1)g t g e   ， 则 3( ) (1)maxg t g e   . 故存在唯一的正数 1t  使得方程 (*)成立， 即存在唯一的负数 1 e et tk     ， 使得 3y kx e   是曲线 ( )y f x 的切线. 16．已知函数 ( R)a . (Ⅰ) 求函数 ( )f x 的单调区间； (Ⅱ) 当 0a  时，求函数 ( )f x 在[1, 2]上最小值. 【答案】(Ⅰ)见解析；(Ⅱ)当0 ln 2a  时，函数 ( )f x 的最小值是 min( )xf a  ；当 ln 2a  时，函数 ( )f x 的最小值是 min( ) ln 2 2f x a  【解析】 (1)函数 ( )f x 的定义域 为 (0, ) ． 1 1( )     axf x a x x 因为 0a  ，令 1( ) 0f x a x ¢ = - = ，可得 1x a  ； 当 10 x a   时， 1( ) 0axf x x     ；当 1x a  时， 1( ) 0axf x x     ， 综上所述：可知函数 ( )f x 的单调递增区间为 10, a       ，单调递减区间为 1 , a      (2)( )i 当 10 1 a   ，即 1a  时，函数 ( )f x 在区间[1, 2]上是减函数， ( )f x 的最小值是 (2) ln 2 2f a  ( )ii 当 1 2 a  ，即 10 2 a  时，函数 ( )f x 在区间[1, 2]上是增函数， ( )f x 的最小值是 (1)f a  ( )iii 当 11 2 a   ，即 1 1 2 a  时，函数 ( )f x 在 11, a       上是增函数，在 1 , 2 a       上是减函数． 又 (2) (1) ln 2f f a   ， 当 1 ln 2 2 a  时， ( )f x 的最小值是 (1)f a  ； 当 ln 2 1a  时， ( )f x 的最小值为 (2) ln 2 2f a  综上所述，结论为当0 ln 2a  时，函数 ( )f x 的最小值是 min( )xf a  ； 当 ln 2a  时，函数 ( )f x 的最小值是 min( ) ln 2 2f x a  . 17．已知函数 ( )f x 满足:①定义为 R；② 2( ) 2 ( ) 9x xf x f x e e      . （1）求 ( )f x 的解析式； （2）若 1 2, [ 1,1]x x   ；均有    2 1 1 2 2( 2) 6 1x a x x f x    … 成立，求 a的取值范围； （3）设 2 ( ), ( 0) ( ) 2 1, ( 0) f x x g x x x x       ，试求方程 [ ( )] 1 0g g x   的解. 【答案】（1） ( ) 3xf x e  （2）[ 3, 7] （3） 3 ， (1 2)  、 ln3， ln(3 ln 4) 、 1 2(1 ln 2)   【解析】 （1） 2( ) 2 ( ) 9x xf x f x e e      ,…① 所以 2( ) 2 ( ) 9x xf x f x e e       即 1( ) 2 ( ) 2 9x xf x f x e e      …② 由①②联立解得: ( ) 3xf x e  . （2）设 2( ) ( 2) 6x x a x      ,    ( ) 1 3 3 3x x xF x x e e xe x      , 依题意知:当 1 1x   时, min max( ) ( )x F x  ( ) ( ) 3 3x x x xF x e e xe xe       又 ( ) (1 ) 0xF x x e     在 ( 1,1) 上恒成立, 所以 ( )F x 在[ 1,1] 上单调递减 ( ) (1) 3 0minF x F e       ( )F x 在[ 1,1] 上单调递增, max( ) (1) 0F x F   ( 1) 7 0 (1) 3 0 a a           , 解得: 3 7a   实数 a的取值范围为[ 3, 7] . （3） ( )g x 的图象如图所示： 令 ( )T g x ,则 ( ) 1g T  1 2 32, 0, ln 4T T T     当 ( ) 2g x   时有 1个解 3 , 当 ( ) 0g x  时有 2个解： (1 2)  、 ln3 , 当 ( ) ln 4g x  时有 3个解: ln(3 ln 4) 、 1 2(1 ln 2)   . 故方程 [ ( )] 1 0g g x   的解分别为： 3 , (1 2)  、 ln3 , ln(3 ln 4) 、 1 2(1 ln 2)   18．已知函数    21 1 ln 2 f x x ax a x    . （1）若 1a  ，讨论函数  f x 的单调性； （2）设      1 lng x f x a x x    ，是否存在实数 a，对任意 1x ，  2 0,x   ， 1 2x x ，有    1 2 1 2 0 g x g x a x x     恒成立？若存在，求出 a的范围；若不存在，请说明理由. 【答案】（1）见解析（2）存在，  2,a  . 【解析】 （1）函数  f x 的定义域为  0 ， ，        2 1 11 11 x x ax ax af x x a a x x x               ， ①若 1 1a   ，则 2a  ，    21 0 x f x x     ，且只在 1x  时取等号，∴  f x 在  0 ， 上单调递增； ②若 1 1a   ，则 2a  ，而 1a  ，∴1 2a  ，当  1,1x a  时，   0f x  ；当  0, 1x a  及  1,  时，   0f x  ，所以  f x 在  1,1a  上单调递减，在  0, 1a  及  1,  上单调递增； ③若 1 1a   ，则 2a  ，同理可得:  f x 在  1, 1a  上单调递减，在  0,1 及  1,a   上单调递增； 综上，当1 2a  时，  f x 在  1,1a  上单调递减，在  0, 1a  及  1,  上单调递增； 当 2a  时，  f x 在  0,  上单调递增； 当 2a  时，  f x 在  1, 1a  上单调递减，在  0,1 及  1,a   上单调递增； （2）    21 2 ln 2 g x x x a x    ， 假设存在 a，对任意 1x ，  2 0,x   ， 1 2x x ，有    1 2 1 2 0 g x g x a x x     恒成立， 不妨设 1 20 x x  ，要使    1 2 1 2 0 g x g x a x x     恒成立，即必有    2 2 1 1g x ax g x ax   ， 令    h x g x ax  ，即      21 1 2 ln 2 h x x a x a x     ，          2 1 2 1 221 x a x a x x aah x x a x x x              ， 要使  h x 在  0,  上为增函数， 只要   0h x  在  0,  上恒成立，须有 2 0x a   ， 2a  ，故存在  2,a  时，对任意 1x ，  2 0,x   ， 1 2x x ，有    1 2 1 2 0 g x g x a x x     恒成立. 19．已知函数     2ln 1f x x ax   ， 0a  . （1）讨论函数  f x 的单调性； （2）若函数  f x 在区间( )1,0- 有唯一零点 0x ，证明： 2 1 0 1e x e    . 【答案】（Ⅰ）见解析;（Ⅱ）见解析. 【解析】 （Ⅰ）   21 2 2 1' 2 1 1 ax axf x ax x x        ， 1x   ， 令   22 2 1g x ax ax   ，  24 8 4 2a a a a     ， 若 0  ，即0 2a  ，则   0g x  ， 当  1,x   时，  ' 0f x  ，  f x 单调递增， 若 0  ，即 2a  ，则   0g x  ，仅当 1 2 x   时，等号成立， 当  1,x   时，  ' 0f x  ，  f x 单调递增. 若 0  ，即 2a  ，则  g x 有两个零点   1 2 2 a a a x a     ，   2 2 2 a a a x a     ， 由    1 0 1 0g g    ， 1 0 2 g       得 1 2 11 0 2 x x      ， 当  11,x x  时，   0g x  ，  ' 0f x  ，  f x 单调递增； 当  1 2,x x x 时，   0g x  ，  ' 0f x  ，  f x 单调递减； 当  2 ,x x  时，   0g x  ，  ' 0f x  ，  f x 单调递增. 综上所述， 当0 2a  时，  f x 在  1,  上单调递增； 当 2a  时，  f x 在  2 1, 2 a a a a           和  2 , 2 a a a a           上单调递增， 在    2 2 , 2 2 a a a a a a a a              上单调递减. （Ⅱ）由（1）及  0 0f  可知：仅当极大值等于零，即  1 0f x  时，符合要求. 此时， 1x 就是函数  f x 在区间  1,0 的唯一零点 0x . 所以 2 0 02 2 1 0ax ax   ，从而有  0 0 1 2 1 a x x    ， 又因为     2 0 0 0ln 1 0f x x ax    ，所以     0 0 0 ln 1 0 2 1 xx x     ， 令 0 1x t  ，则 1ln 0 2 tt t    ， 设   1 1ln 2 2 h t t t    ，则   2 2 1' 2 th t t   ， 再由（1）知： 10 2 t  ，  ' 0h t  ，  h t 单调递减， 又因为   2 2 5 0 2 eh e    ，  1 3 0 2 eh e    ， 所以 2 1e t e   ，即 2 1 0 1e x e    20．已知函数   2lnf x x ax x   ，a R . （1）若 1a  ，试求函数  f x 的零点个数； （2）当 1a   ，对 1 0x  ， 2 0x  且满足    1 2 1 2 1 f x f x x x     ，试判断 1 2x x 与 5 1 2  的大小关系， 并说明理由. 【答案】（1）一个零点；（2） 1 2 5 1 2 x x    ，理由见解析 【解析】 （1）当 1a  时，   2lnf x x x x   ， 0x  ， 此时     2 1 11 2 1' x x x f x x x       ， 则当 0 1x  时，  ' 0f x  ；当 1x  时，  ' 0f x  ； 易知函数  f x 在区间  0,1 单调递增，在区间  1, 单调递减； 所以      max 1 0f x f x f   （当且仅当 1x  取等号）， 故当 1a  时，函数  f x 只有一个零点； （2） 1 2 5 1 2 x x    ，理由如下：当 1a   时，   2ln xf x x x   ， 0x  ， 由    1 2 1 2 1 f x f x x x     ，即 2 2 1 1 1 2 2 2 1 2ln lnx x x x x x x x        ， 从而    2 1 2 1 2 1 2 1 2lnx x x x x x x x       ，令 1 2t x x  ， 则由   lng t t t  ，得   1' tg t t   ， 可知，  g t 在区间  0,1 上单调递减，在区间  1, 上单调递增. 所以有    1 1g t g  ，所以    2 1 2 1 2 1x x x x    ， 因此， 1 2 5 1 2 x x    ，由上可知，这里取到等号需要 1 2 1x x  ， 而此时 1 2 1 1 1 5 1 2 x x x x      无实数解，故必有 1 2 5 1 2 x x    . 21．已知函数   2xf x e ax   ，其中a为常数. （1）求函数  f x 的单调区间； （2）若 2y ex  是   2xf x e ax   的一条切线，求a的值； （3）已知 1a  ， k为整数，若对任意  0,x  ，都有    ' 1 0x k f x x    恒成立，求 k的最大值. 【答案】(1)答案见解析；(2)0；(3)2. 【解析】 （1）函数  f x 的定义域为    , , xf x e a    ． 若 0a  时，则   0f x  ，所以  f x 在  ,  上单调递增； 若 0a  时，则当  , lnx a  时，   0f x  ，当  ln ,x a  时，   0f x  ， 所以  f x 在  , lna 上递减，在  ln ,a  上递增． （2）设切点为  0 0,x y 则： 0 0 0 0 0 0 2 2 x x e a e y ex y e ax           ，解得 0 0 1 0 , 0 2 x a a y e         ． （3）当 1a  时，对任意  0,x  ，都有     1 0x k f x x    恒成立等价于 1 1x xk x e     对 0x  恒 成立． 令   1 ( 0) 1x xg x x x e      ，则      2 2 1 x x x e e x g x e      ， 由（1）知，当 1a  时，   2xf x e x   在  0, 上递增． 因为    0 0 2 0f f， ，所以   2xf x e x   在  0, 上存在唯一零点， 所以  g x 在  0, 上也存在唯一零点，设此零点为 0x ，则  0 1,2x  ． 因为当  00,x x 时，   0g x  ，当  0 ,x x  时，   0g x  ， 所以  g x 在  0, 上的最小值为   0 0 0 0 1 1x xg x x e     ，所以 0 0 0 1 1x xk x e     ， 又因为   0 0 0 2 0xg x e x    ，所以 0 0 2xe x  ，所以 0 1k x  ． 又因为 k为整数且 02 1 3x   ，所以 k的最大值是 2． 22．已知函数    21 1 ln 2 f x x m x m x    ，m R ，   xeg x x  . (1)求  g x 的极值； (2)若对任意的   1 2 1 2, 2, 4x x x x  ，当 1 2x x 时，        1 2 1 2f x f x g x g x   恒成立，求实数m的 最大值； (3)若函数  f x 恰有两个不相等的零点，求实数m的取值范围. 【答案】(1)  g x 的极小值为 e，无极大值；(2) 2 2 2 e  ；(3) 1 ,0 2      . 【解析】 (1)     2 1xe x g x x    ，令   0g x  ，得 1x  . 列表如下： x  0,1 1  1,  g x － 0 ＋  g x 极小值 ∵  1 1g  ，∴  y g x 的极小值为 e，无极大值. (2)∵ 2 1x x ，由(1)可知        1 2 1 2f x f x g x g x   等价于        1 2 2 1f x f x g x g x   ， 即        1 1 2 2f x g x f x g x   . 设        21 ln 1 2 xeh x f x g x x m x m x x        ，则  h x 在 2,4 为增函数. ∴       2 1 11 0 x xe xm x eh x x m x m x x x x                在 2,4 恒成立. ∴ xem x x   恒成立. 设   xev x x x   ，∵     2 1 1 0 xe x v x x      在 2,4 上恒成立 ∴  v x 为增函数. ∴  v x 在 2,4 上的最小值为   2 2 2 2 ev   . ∴ 2 2 2 em   ，∴m的最大值为 2 2 2 e  . (3)       1 1 x x mmf x x m x x         ①当0 1m  时，当  0,x m 和  1, 时，   0f x  ，  f x 单调递增 当  ,1x m 时，   0f x  ，  f x 单调递减 所以  f x 的极大值为    21 1 ln 2 f m m m m m m    2 ln 0 2 m m m m     所以函数  f x 至多一个零点 ②当 1m  时，    21 0 x f x x     ，  f x 在  0,  上单调递增. ③当 1m > 时，当  0,x m 和  1, 时，   0f x  ，  f x 单调递增 当  ,1x m 时，   0f x  ，  f x 单调递减 所以  f x 的极大值为    1 11 1 0 2 2 f m m        f x 的极小值为    1 0f m f  所以函数  f x 至多有一个零点. ④当 0m  时，当  0,1x ，   0f x  ，  f x 单调递增 当  1,x  时，   0f x  ，  f x 单调递减 所以    min 1 11 1 2 2 f m m      Ⅰ：当  min 11 0 2 f m    时，即 1 2 m   时，函数  f x 至多一个零点. Ⅱ：当 1 0 2 m   时，    3 1 ln 0 2 mf m m m          所以存在  1 ,1x m  ，  1 0f x  所以函数  f x 在  0,1 上有唯一的零点. 又     2 2 2 21 2 0 2 ef e e e m           所以函数  f x 在  1, 上有唯一的零点. 综上所述：实数m的取值范围为 1 ,0 2      . 23．已知函数   ln 2sinf x x x x   ,  f x 为  f x 的导函数. (1)求证:  f x 在  0 ， 上存在唯一零点; (2)求证:  f x 有且仅有两个不同的零点. 【答案】(1)证明见解析;(2)证明见解析. 【解析】 (1)设     1 1 2cosg x f x x x     ， 当  0,x  时，   2 12sin 0g x x x      ，所以  g x 在  0, 上单调递减， 又因为 3 1 1 0 3 g            ， 2 1 0 2 g           所以  g x 在 , 3 2        上有唯一的零点 ，所以命题得证． (2) ①由(1)知：当  0,x  时，   0f x  ，  f x 在  0, 上单调递增; 当  ,x   时，   0f x  ，  f x 在  ,  上单调递减; 所以  f x 在  0, 上存在唯一的极大值点 3 2         所以   ln 2 2 0 2 2 2 2 f f                又因为 2 2 2 2 1 1 1 12 2sin 2 2 0f e e e e               所以  f x 在  0, 上恰有一个零点． 又因为   ln 2 0f         所以  f x 在  ,  上也恰有一个零点． ②当  , 2x   时， sin 0x  ，   lnf x x x  设   lnh x x x  ，   1 1 0h x x     所以  h x 在 , 2  上单调递减，所以     0h x h   所以当  , 2x   时，       0f x h x h    恒成立 所以  f x 在 , 2  上没有零点． ③当  2 ,x   时，   ln 2f x x x   设   ln 2x x x    ，   1 1 0x x     所以  x 在 2 ,  上单调递减，所以    2 0x    所以当  2 ,x   时，      2 0f x x     恒成立 所以  f x 在 2 ,  上没有零点． 综上，  f x 有且仅有两个零点． 24．已知函数   2xf x e mx  ，其中 0m  ． （1）当 1m   时，求曲线  y f x 在点   0, 0f 处的切线方程； （2）若不等式   0f x  在定义域内恒成立，求实数m的取值范围． 【答案】(1) 1y x  ;(2)  2 ,0m e  . 【解析】 （1）当 1m   时，   2xf x e x  ∴   22 1xf x e   则  0 1f   ，又  0 1f  ∴曲线  y f x 在点   0, 0f 处的切线方程为： 1y x  （2）函数  f x 定义域为  ,  ，且   22 xf x e m    0m  下面对实数m进行讨论： ①当 0m  时，   2 0xf x e  恒成立，满足条件 ②当 0m  时，由   0f x  解得 1 ln 2 2 mx       ，从而知 函数  f x 在 1 ln , 2 2 m         内递增；同理函数  f x 在 1, ln 2 2 m         内递减， 因此  f x 在 1 ln 2 2 mx       处取得最小值 ln 1 2 2 m m        ∴ ln 1 0 2 2 m m         ， 解得 2 0e m   综上：当  2 ,0m e  时，不等式   0f x  在定义域  ,  内恒成立. 25．已知函数 ( ) ln( 1) 1xf x e x ax x     ． （1）若 0a  ，证明：   0f x  ． （2）若函数  f x 在 0x  处有极大值，求实数 a的取值范围． 【答案】（1）见解析；（2） 1 2 a  【解析】 （1）若 0a  ， ( ) 1xf x e x   ， ( ) 1xf x e  ，由 ( ) 0f x  得 0x  ，由由 ( ) 0f x  得 0x  ， 所以 ( ) 1xf x e x   在( ), 0-¥ 单调递减，在( )0,+¥ 单调递增， 所以  ( ) 1 0 0xf x e x f     恒成立； （2） ( ) ln( 1) 1xf x e x ax x     ，  1,x   ， ( ) 1 ln( 1) 1 x xf x e a x x          ， 0(0) 1 0 0f e a     ， 函数  f x 在 0x  处有极大值， 即 1( ) 1 ln( 1) 1 ln( 1) 1 1 1 x xxf x e a x e a x x x                       ， 在 0x  处左正右负，且在 0x  处连续， 必存在 0  ，  ,x    ， 必有  , 0x   ， ( ) 0f x  ，  0, , ( ) 0x f x   ， 记  2 l 1( ) 1 1 xf x e a x x            ， 若  2 l 10, ( ) 0 1 1 xa f x e a x x             恒成立， 则 ( ) 1 ln( 1) 1 x xf x e a x x          在定义域单调递增， 0, ( ) (0) 0x f x f    ，不合题意，舍去； 若    2 2 1 l 1 l 10 , 0, 2, 2 2 1 1 1 1 1 ,xa x e a a x xx x                    2 l 1( ) 1 2 0 1 1 xf x e a a x x               ， ( )f x 在  0,x  上单调递增， 即  0, , ( ) (0) 0x f x f     ，不合题意，舍去； 当  2 1 l 1, ( ) 2 1 1 xa f x e a x x            单调递增， (0) 1 2 0f a    ，必存在 0  ，使得当  ,x    时， ( ) 0f x  ， 此时 ( )f x 在  ,x    单调递减， 0(0) 1 0 0f e a     必有  , 0x   ， ( ) 0f x  ，  0, , ( ) 0x f x   ， 即函数  f x 在  , 0x   递增，在  0,x  递减，即函数  f x 在 0x  处有极大值， 综上所述： 1 2 a  26．已知定义域为 R的函数 ( ) n nf x x （ *n N ， 2n  ） （1）设 2 1( ) ( ) (1 )n nF x f x f x   ，求 ( )F x 的单调区间； （2）设 ' ( )nf x 为 ( )nf x 导数， （i）证明：当 2a  ， 0x  时， 1xa x a   ； （ii）设关于 x的方程 ' ' 1 1 (1 ) 2 1 (1 ) 2 1 n n n n f x f x        的根为 0x ，求证： 00 1x  【答案】（1）当n为奇数时 ( )F x 的增区间为 2 1( , ) 3 1 n n    ，减区间为 2 1( , ) 3 1 n n    ；当 n为偶数时 ( )F x 的 增区间为 2 1( , ) 3 1 n n    及 (1, ) ，减区间为 2 1( ,1) 3 1 n n   ． （2）（i）证明见解析，（ii）证明见解析． 【解析】 （1）    2 1 1 nnF x x x  ， 当 *n N ， 2n  时        2 2 12 1' 2 1 1 1n n nnF x n x nx x      即            1 12 2 2 2 2 1' 1 2 1 1 3 1 1 3 1 n nn n nF x x x n x nx n x x x n                    （a）当 n为大于 1的奇数时， 1n 是偶数，   11 0nx   ， 2 2 0nx   ，3 1 0n   当 2 1 3 1 nx n    时，  ' 0F x  ，当 2 1 3 1 nx n    时  ' 0F x  故  F x 的增区间为 2 1, 3 1 n n     ，减区间为 2 1 , 3 1 n n     当n为偶数时， 1n 是奇数，由于 2 1 1 3 1 n n    ，所以 当 2 1 3 1 nx n    或 1x  时，  ' 0F x  ，当 2 1 1 3 1 n x n     时  ' 0F x  故  F x 的增区间为 2 1, 3 1 n n     及  1, ，减区间为 2 1 ,1 3 1 n n      综上，当 n为奇数时  F x 的增区间为 2 1, 3 1 n n     ，减区间为 2 1 , 3 1 n n     ， 当n为偶数时  F x 的增区间为 2 1, 3 1 n n     及  1, ，减区间为 2 1 ,1 3 1 n n      ， （2）（i）证明：设   1xx a x a    ， 0x  ，则   1' ln 1xx a a   ， 因为 2 1a   ， ln ln2 0a   ，故  ' x 在  0, 是增函数， 从而    ' ' 0 ln 1x a a    ，由于 2a  ， ln ln2 0a   所以 ln 2ln ln4 1a a a   ，  ' 0x  所以  x 在  0, 是增函数，    0 0x   ，即 1xa x a   （ii）  ' 1n nf x nx  ，原方程化为           1 1 1 2 1 1 1 2 11 1 n n n n n x n n xn x           解得     0 1 2 1 1 2 1 n n n x n      ，因为 2n  ，所以 0 0x  ； 作差得，     1 0 2 21 1 2 1 n n nx n       ， 由（i）知，当 2a  ， 0x  时， 1xa x a   ， 令 2a  ， x n ，故有 12 2n n   ，所以 0 1 0x   ， 0 1x  ， 综上， 00 1x  27．设函数   2 sinf x x x    ， 0, 2 x     ，   22 cos 2 2 x mg x x x           ，  m R . （1）证明：   0f x  ； （2）当 0, 2 x     时，不等式   4 g x   恒成立，求m的取值范围. 【答案】(1)证明见解析 (2) 2 2 8 ,     【解析】 （1） 2( ) cosf x x     在 0, 2 x     上单调递增， 2 2( ) 1,f x         ， 所以存在唯一 0 0, 2 x      ，  0 0f x  .当  00, , ( ) 0x x f x  ，  f x 递减； 当 0, , ( ) 0 2 x x f x       ，  f x 递增. 所以 max( ) max (0), 0 2 f x f f          ， ( ) 0,0 2 f x x      （2） 2( ) sin 2 xg x x m x            ， 2( ) cosg x x m      当 0m 时，   0g x  ，  g x 在 0, 2 x     上单调递减， min( ) 2 4 g x g         ，满足题意 当 2 0m     时，  g x 在 0, 2 x     上单调递增， 2(0) 1 0g m       ， 2 0 2 g m          ， 所以存在唯一 1 0, 2 x      ，  1 0g x  . 当    10, , 0x x g x  ，  g x 递减；当  1, , 0 2 x x g x       ，  g x 递增 而 (0) 0 2 g m    ， 0 2 g       .所以存在唯一  2 20, , 0 2 x g x       . 当  20, , ( ) 0x x g x  ，  g x 递增；当 2, , ( ) 0, ( ) 2 x x g x g x       递减. 要0 2 x    时， ( ) 4 g x   恒成立，即 2 (0) 4 2 8 2 4 g m g                 所以 2 2 8 0m     当 2m    时， ( ) 0g x  ，当 0, 2 x     ，  g x 递减， 0, ( ) 0 2 g g x       ( )g x 在 0, 2 x     递增， ( ) 2 4 g x g         与题意矛盾 综上：m的取值范围为 2 2 8,     28．已知函数     21ln 1 2 f x ax a x x    ，   1xg x e x   . （Ⅰ）若 0x  为函数  f x 的极小值点，求 a的取值范围，并求  f x 的单调区间； （Ⅱ）若 0x  ，     21 2 g x f x x  ，求 a的取值范围. 【答案】（Ⅰ） 1a  ，  f x 的递减区间  1,0 和  1,a   ，递增区间为  0, 1a  ，（Ⅱ） 1a  【解析】 （Ⅰ）由题意知：  1,x   ，且    1 1 x x aaf x a x a x x            ， 若 1 0a   ，即 1a  时，当 0x  ，   0f x  ，所以 0x  不可能为  f x 的极小值点； 若 1 0a   ，即 1a  时，令   0 0 1f x x a      ； 令   0 1 0f x x      或 1x a  ， 所以  f x 的递减区间  1,0 和  1,a   ，递增区间为  0, 1a  ， 所以 0x  为函数  f x 的极小值点， 综上： 1a  ，  f x 的递减区间  1,0 和  1,a   ，递增区间为  0, 1a  . （Ⅱ）令            21 ln 1 1 1 0 2 xF x g x f x x e a x a x x          ， 则  0 0F  ，      11 1 1 1 1 1 1 x x xa xF x e a e a e x ax x x x                 ， 令       1 1 0xg x e x ax x     ，则  0 0g  ， 因为      2 1xg x x e a     ，令     0h x g x x  ， 则    3 0xh x x e    ，  0x  ， 所以  g x 在 0, 上单调递增，所以    0 1g x g a    ， （1）当1 0a  ，即 1a  时，   0g x  ， 0x  ，所以  g x 在 0, 上单调递增，所以   0g x  对 0x  恒成立. 所以    1 0 1 F x g x x     恒成立，所以  F x 在  0, 上单调递增，所以    0 0F x F  ， 0x  ， 符合题意； （2）当1 0a  ，即 1a  时，因为  0 1 0g a    ， 又 1 0a   且        11 1 1 1 1 0ag a a e a a a           ， 又  g x 在  0, 上连续且单调递增，所以存在 0 0x  ，使得  0 0g x  ，此时，当  00,x x 时，   0g x  ，所以  g x 单调递减，所以    0 0g x g  ， 所以    1 0 1 F x g x x     ，所以  F x 在  00,x x 单调递减， 所以    0 0F x F  ，  00,x x ，矛盾，舍去. 综上： 1a  . 29．已知函数    ln x af x a R x    ，   e 1xg x   ． （1）求  f x 的单调区间； （2）若    g x f x 在  0,  上恒成立，求 a的取值范围． 【答案】（1） ( )f x 的单调递增区间为  10,e a ，单调递减区间为  1e +a ， （2）  ,1 【解析】 （1） 2 1 ln'( ) x af x x    ( 0)x  . 当 10 e ax   时， '( ) 0, ( )f x f x 单调递增； 当 1e ax  时， '( ) 0, ( )f x f x 单调递减. 所以 ( )f x 的单调递增区间为  10,e a ，单调递减区间为  1e +a ， (2)由 ( ) ( )g x f x 得 lne 1x x a x    也就是 e lnxa x x x   ，令 ( ) e lnxh x x x x   则 1'( ) e e 1x xh x x x     = 1( 1)(e )xx x   ，由 0x  知， 1 0x   . 设 1( ) ext x x   ， 2 1'( ) e 0xt x x    ， ( )t x 在  0,  单调递增， 又 1( ) e 2 0, (1) e 1 0 2 t t      ，所以存在 0 1 ,1 2 x （ ）使得 0( ) 0t x  ， 即 0x 0 1e x  . 当  00,x x 时， '( ) 0h x  ， ( )h x 在  00, x 单调递减； 当  0 ,x x  时， '( ) 0h x  ， ( )h x 在  0 ,x  单调递增; 所以 0 min 0 0 0 0( ) ( ) e lnxh x h x x x x    = 0 01 1x x   . 所以 a的取值范围是  ,1 . 30．已知 1( ) lnmf x x m x x     ，mR . （1）讨论 ( )f x 的单调区间； （2）当 2 0 2 em  时，证明： 2 ( ) 1xe x xf x m    . 【答案】（1） ( )f x 在 (1, 1)m  上单调递减；在 (0,1)和 ( 1, )m   上单调递增.（2）见解析 【解析】 （1） ( )f x 的定义域为 (0, ) ， 2 2 1 ( 1)[ ( 1)]( ) 1 m m x x mf x x x x         ， 当 1m £ 时，由 ( ) 0f x  ，得 1x  ； 由 ( ) 0f x  ，得 0 1x  ， 所以 ( )f x 在 (0,1)上单调递减，在 (1, ) 上单调递增； 当1 2m  时，由 ( ) 0f x  ，得 1x  或0 1x m   ； 由 ( ) 0f x  ，得 1 1m x   ； 所以 ( )f x 在 ( 1,1)m  上单调递减，在 (0, 1)m  和 (1, ) 上单调递增； 当 2m  时，由 2 2 ( 1)( ) 0xf x x    ，得 ( )f x 在 (0, ) 上单调递增； 当 2m  时，由 ( ) 0f x  ，得 1x m  或 0 1x  ；由 ( ) 0f x  ，得1 1x m   ； 所以 ( )f x 在 (1, 1)m  上单调递减；在 (0,1)和 ( 1, )m   上单调递增. （2）由 2 ( ) 1xe x xf x m    ，得 lnxe mx x ， ①当0 1x  时， e 1x  ， ln 0mx x  ，不等式显然成立； ②当 1x  时， ln 0x x  ，由 2 0 2 em  ，得 2 0 ln ln 2 emx x x x  ， 所以只需证： 2 ln 2 x ee x x ， 即证 22 ln 0 xe x x    ，令 22( ) ln xeg x x x    ， 则 2 2 2 ( 1)( ) xe x xg x x      ， 1x  ， 令 2( ) 2 ( 1)xh x e x x   ， 则 2( ) 2 1xh x xe   ， 令 ( ) ( )h x x  ， 则 2( ) 2( 1) 0xx x e     ， 所以 ( )h x 在 (1, ) 上为增函数， 因为 2(1) 1 0h e     ， (2) 3 0h   ， 所以存在 0 [1,2]x  ，  0 0h x  ， 所以 ( )h x 在 01, x 上单调递减，在 0 ,x  上单调递增， 又因为 (1) 1 0h    ， (2) 0h  ， 当 [1, 2)x 时， ( ) 0g x  ， ( )g x 在[1,2)上单调递减， 当 [2, )x  时， ( ) 0g x  ， ( )g x 在[2, ) 上单调递增， 所以 ( ) (2) 1 ln 2 0g x g    ， 所以 ( ) 0g x ， 所以原命题得证 31．已知函数   3 21 ( 1) 3 2 a x x axf x     . （Ⅰ）当 1a  时，求曲线  y f x 在点 (0, (0))f 处的切线方程； （Ⅱ）讨论函数  f x 的单调性； （Ⅲ）对于任意 1x ， 2 [0 2]x  , ，都有 1 2 2 ( ) ( ) 3 f x f x  ，求实数 a的取值范围. 【答案】（Ⅰ） y x ；（Ⅱ）分类讨论，详见解析；（Ⅲ） 1 5, 3 3      . 【解析】 解：（Ⅰ）当 1a  时，因为   3 21 3 x x xf x    所以   2 2 1x xf x    ， (0) 1f   . 又因为 (0) 0f  ， 所以曲线 ( )y f x 在点  0, (0)f 处的切线方程为 y x . （Ⅱ）因为   3 21 ( 1) 3 2 a x x axf x     ， 所以 2( ) ( 1) 0f x x a x a      . 令 ( ) 0f x  ，解得 x a 或 1x  . 若 1a  ，当   0f x  即 1x  或 x a 时， 故函数 ( )f x 的单调递增区间为    ,1 , ,a  ； 当   0f x  即1 x a  时，故函数 ( )f x 的单调递减区间为  1,a . 若 1a  ，则 2 2( ) 2 1 ( 1) 0f x x x x       ， 当且仅当 1x  时取等号，故函数 ( )f x 在  ,  上是增函数. 若 1a  ，当 ( ) 0f x  即 x a 或 1x  时， 故函数 ( )f x 的单调递增区间为    , , 1,a  ； 当 ( ) 0f x  即 1 a x 时，故函数 ( )f x 的单调递减区间为  ,1a . 综上， 1a  时，函数 ( )f x 单调递增区间为 ( 1) ( )a , , ,+ ，单调递减区间为 (1, )a ； 1a  时，函数 ( )f x 单调递增区间为 ( , )  ； 1a  时，函数 ( )f x 单调递增区间为 ( ) (1 )a , , ,+ ，单调递减区间为 ( ,1)a . （Ⅲ） 由题设，只要    max min 2 3 f x f x  即可. 令 2( ) ( 1) 0f x x a x a      ，解得 x a 或 1x  . 当 0a  时，随 x变化， ( ), ( )f x f x 变化情况如下表： x 0  0,1 1  1,2 2  f x  0   f x 0 减 极小值 增 2 3 由表可知 (0) 0 (1)f f  ，此时 2 (2) (1) 3 f f  ，不符合题意. 当0 1a  时，随 x变化，    'f x f x, 变化情况如下表： x 0  0,a a  ,1a 1  1,2 2  f x  0  0   f x 0 增 极大值 减 极小值 增 2 3 由表可得 3 21 1 1 1 2 (0) 0 ( ) (1) (2) 6 2 2 6 3 f f a a a f a f      , , , ， 且 (0) ( )f f a ， (1) (2)f f ， 因     22 0 3 f f  ，所以只需 ( ) (2) (1) (0) f a f f f    ， 即 3 21 1 2 6 2 3 1 1 0 2 6 a a a         ，解得 1 1 3 a  . 当 1a  时，由（Ⅱ）知  f x 在 0,2 为增函数， 此时        max min 22 0 3 f x f x f f    ，符合题意. 当1 2a  时， 同理只需 (1) (2) ( ) (0) f f f a f    ，即 3 2 1 1 2 2 6 3 1 1 0 6 2 a a a         ，解得 51 3 a  . 当 2a  时， 2( ) (1 ) 3 2f f  ，   2( ) 0 ( 3 1 1)ff f  ，不符合题意. 综上，实数a的取值范围是 1 5, 3 3      . 32．已知函数 ( ) ln ,f x x x kx k R   . （1）求 ( )y f x 在点 (1, (1))f 处的切线方程； （2）若不等式 2( )f x x x  恒成立，求 k的取值范围； （3）求证：当 *n N 时，不等式   2 2 1 2ln 4 1 2 1 n i n ni n     成立. 【答案】（1） ( 1) 1y k x   （2） k 2 （3）证明见解析 【解析】 （1）函数 ( )y f x 的定义域为 (0, ) ， ( ) 1 lnf x x k    ， (1) 1f k   ， ∵ (1)f k ，∴函数 ( )y f x 在点 (1, (1))f 处的切线方程为 ( 1)( 1)y k k x    ， 即 ( 1) 1y k x   . （2）由 2( )f x x x  ， ( ) lnf x x x kx  ，则 2lnx x kx x x   ，即 ln 1x k x   ， 设 ( ) ln 1g x x x k    ， 1( ) 1g x x    ，  0,1x ，   0g x  ， ( )g x 单调递增，  1,x  ， ( ) 0g x  ， ( )g x 单调递减， ∵不等式 2( )f x x x  恒成立，且 0x  ， ∴ ln 1 0x x k    ，∴ max( ) (1) 2 0g x g k    即可，故 k 2 . （3）由（2）可知：当 2k  时， ln 1x x  恒成立， 令 2 1 4 1 x i    ，由于 *i N ， 2 1 0 4 1i   . 故， 2 2 1 1ln 1 4 1 4 1i i     ，整理得：  2 2 1ln 4 1 1 4 1 i i     ， 变形得：  2 1ln 4 1 1 (2 1)(2 1) i i i      ，即：  2 1 1ln 4 1 1 2 2 1 2 1 i i i         1,2,3, ,i n  时， 1 1ln3 1 1 2 3        ， 1 1ln5 1 1 2 3        ……，  2 1 1 1ln 4 1 1 2 2 1 2 1 n n n         两边同时相加得：   2 2 2 1 1 1 2 2ln 4 1 1 2 2 1 2 1 2 1 n i n n ni n n n n             ， 所以不等式在 *n N 上恒成立. 33．已知函数 2( ) ln ( 0)f x x x ax a   . （1）当 1a  时，求  f x x 的最大值； （2）若  f x 只有一个极值点 0x . （i）求实数 a的取值范围； （ii）证明：  0 1f x e   . 【答案】(1) 最大值为-1. (2) （i） 0a  （ii）证明见解析 【解析】 （1）当 1a  时，   ln f x x x x   ， 0x  . 令   lng x x x  ，则   1 1g x x    ， ∴  g x 在  0,1 上单调递增，在  1, 上单调递减 ∴ max( ) (1) 1g x g   ，故  f x x 的最大值为-1. （2） ( ) 1 ln 2f x x ax    ， 1( ) 2f x a x    . ①当 0a  时，   0f x  在  0,  恒成立，则  f x 在  0,  单调递增. 而 1 2 0af e e          ，当 0 1x  时， ( ) 1 ln 2 1 ln 2f x x ax x a       ， 则  2 1 0af e   ，且 2 1 1ae e   ，∴ 2 1 0 1,ax e e       使得  0 0f x  . ∴当  00,x x 时，   0f x  ，则  f x 单调递减； 当  00,x x 时，   0f x  ，则  f x 单调递增，∴  f x 只有唯一极值点 0x . ②当 0a  时， 1 1( ) 2 0 2 f x a x x a       当 10, 2 x a      时，   0f x  ，则  f x 单调递增； 当 1 , 2 x a       时，   0f x  ，则  f x 单调递减，∴ max 1( ) ln 2 2 f x f a a          . （i）当 2 1a  即 1 2 a  时，   0f x  在  0,  恒成立，则  f x 在  0,  单调递减，无极值点，舍去. （ii）当0 2 1a  即 10 2 a  时， 1 ln 2 0 2 f a a          . 又 1 2 0af e e          ，且 1 1 2e a  ，∴ 1 1 1, 2 x e a      使得  1 0f x  . 由（1）知当 0x  时， ln 1x x  ，则 ln 2 ln 2( 1) 2 1x x x x     ∴ ( ) 1 ln 2 2 2 2 (1 )f x x ax x ax x a x        则 2 1 0f a       ，且 2 1 1 2a a  ，∴ 2 2 1 1, 2 x a a      使得  2 0f x  . ∴当  10,x x 时，   0f x  ，则  f x 单调递减； 当  1 2,x x x 时，   0f x  ，则  f x 单调递增； 当  2 ,x x  时，   0f x  ，则  f x 单调递减. ∴  f x 有两个极值点 1x ， 2x ，舍去. 综上，  f x 只有一个极值点时， 0a  ∵  0 0 01 ln 2 0f x x ax     ，∴ 0 0 1 ln 2 xa x   ， 2 1 0 1,ax e e      ∴    2 0 0 0 0 0 0 1ln ln 1 2 f x x x ax x x    ， 2 1 0 1,ax e e      . 令 1( ) (ln 1) 2 x x x   ，∴ 1( ) ln 0 2 x x    ，则  x 在 2 1 1,ae e       单调递减 ∴当 2 1 1,ax e e      时， 1 1( )x e e          ，∴    0 0 1f x x e    . 34．已知函数 2 2( ) 1 lnf x x a x ax    ( )a R . （1）当 0a  时，讨论函数 ( )f x 的单调性； （2）若 0a  且 (0,1)x ，求证： 2( ) 1 1x f x x e x    . 【答案】(1)答案见解析；(2)证明见解析. 【解析】 （1）函数  f x 的定义域为  0,       2 2 2 2 1 11 2 12 ax axa x axf x a x a x x x          ①若 0a  时，则   0f x  ，  f x 在  0,  上单调递减； ②若 0a  时，当 1x a  时，   0f x  当 10 x a   时，   0f x  ；当 1x a  时，   0f x  故在 10, a       上，  f x 单调递减；在 1 , a      上，  f x 单调递増 （2）若 0a  且  0,1x ，欲证   2 1 1x f x x e x    只需证 21 ln 1 1x x x e x     即证    31 ln 1 xx x x x e    设函数    1 lng x x x  ，   0,1x ，则   lng x x   当  0,1x 时，   0g x  ；故函数  g x 在  0,1 上单调递增 所以    1 1g x g  设函数    31 xh x x x e   ，则    2 32 3 xh x x x x e     设函数   2 32 3p x x x x    ，则   21 6 3p x x x    当  0,1x 时，    0 1 8 0p p     故存在  0 0,1x  ，使得  0 0p x  从而函数  p x 在  00, x 上单调递增；在  0 ,1x 上单调递减 当  00,x x 时，    0 0 2p x p  当  0 1x x ， 时，    0 1 0p x p  故存在  1 0,1x  ，使得  1 0h x  即当  10,x x 时，   0p x  ，当  11x x ，时，   0p x  从而函数  h x 在  10, x 上单调递增；在  11x，上单调递减 因为    0 1, 1h h e  故当  0,1x 时，    0 1h x h  所以      31 ln 1 , 0,1xx x x x e x     即    2 1 1, 0,1x f x x x e x     35．已知函数     2ln 1 af x x x a     （ 0a  ） （1）讨论函数  f x 在  0,  上的单调性； （2）若 0a  且  f x 存在两个极值点，记作 1x ， 2x ，若    1 2 4f x f x  ，求 a的取值范围； （3）求证：当 1a  时，   1 1 1 1xf x e x   （其中 e为自然对数的底数） 【答案】（1）答案不唯一，见解析；（2）  1, 2 ；（3）见解析 【解析】 解：（1）     2ln 1 af x x x a               2 2 2 21 12 1 1 x a a f x a x x a x x a                  （※） 当 2a  时， 0x > ，         2 2 2 0 1 x a a f x x x a        ，函数  f x 在  0,  上是增函数 当0 2a  时,由   0f x  得  2 2 0x a a   ,解得  1 2x a a   （舍去）  2 2x a a  所以当  20,x x 时,  2 2 0x a a   ,从而   0f x  ,函数  f x 在  20, x 上是减函数; 当  2 ,x x  时,  2 2 0x a a   ,从而   0f x  ,函数   0f x  在  2 ,x  上是增函数 综上，当 2a  时,函数  f x 在  0,  上是增函数; 当0 2a  时,函数  f x 在   0, 2a a 上是减函数,在   2 ,a a  上是增函数 （2）由（1）知,当 2a  时,   0f x  ,函数  f x 无极值点 若  f x 存在两个极值点,又由 a为正数必有0 2a  ，由（1）极值点为  1 2x a a   ,  2 2x a a  依题意  2 1a a    即  2 1a a  化为  21 0a   ,得 1a  所以 a的取值范围是    0,1 1,2U 由（※）式得   1 2 1 2 0 2 x x x x a a              1 2 1 2 1 2 2 2ln 1 ln 1a af x f x x x x a x a                1 2 1 2 1 2 2 1 2 1 2 2 2 ln 1 a x x a x x x x x x a x x a                 2 2 2 2 4 2ln 1 ln 1 2 2 1 aa a a a a a                不等式    1 2 4f x f x  化为  2 21 2 0 1 a a        令     1 0,1 1,2a t a    所以    1,0 0,1t   当  1,0t  时,     22ln 2g t t t     ,  ln 0t  , 2 0 t  ,所以   0g t  ,不合题意 当  0,1t 时,   22 ln 2g t t t    ,     2 2 2 11 12 2 0 t g t t t t             所以  g t 在  0,1 上是减函数,所以     21 2ln1 2 0 1 g t g     ,适合题意,即  1,2a 综上,a的取值范围是  1, 2 . （3）当 1a  时,     2ln 1 1 f x x x     不等式   1 1 1 1xf x e x   可化为   1 1 1ln 1 1 xx x e     ，即证 1 1ln xx x e   . 设   1lnh x x x   ,则   2 2 1 1 1xh x x x x     在  0,1 上,   0h x  ,  h x 是减函数;在  1, 上,   0h x  ,  h x 是增函数,所以    1 1h x h  , 设   1 xx e   ,则  x 是减函数,所以    0 1x   , 所以    x h x  ，即 1 1ln xx x e   所以当 1a  时，不等式   1 1 1 1xf x e x  