辽宁省葫芦岛市2020届高三第二次模拟考试数学（文）试题 Word版含答案 12页

‎2020年学 校 姓 名 考 号 ‎………………………………………………装…………订…………线………………………………………………‎ 葫芦岛市普通高中高三第二次模拟考试 数 学（供文科考生使用）‎ 注意事项:‎ ‎1.本试卷分第Ⅰ卷、第Ⅱ卷两部分，共6页．满分150分；考试时间：120分钟.‎ ‎2.答题前，考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B铅笔涂在答题卡上．‎ ‎3.用铅笔把第Ⅰ卷的答案涂在答题卡上，用钢笔或圆珠笔把第Ⅱ卷的答案写在答题纸的相应位置上．‎ ‎4.考试结束，将答题卡和答题纸一并交回．‎ 第Ⅰ卷（选择题，共60分）‎ 一、选择题：本题共12个小题,每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．集合，，则 A. B． C. D. 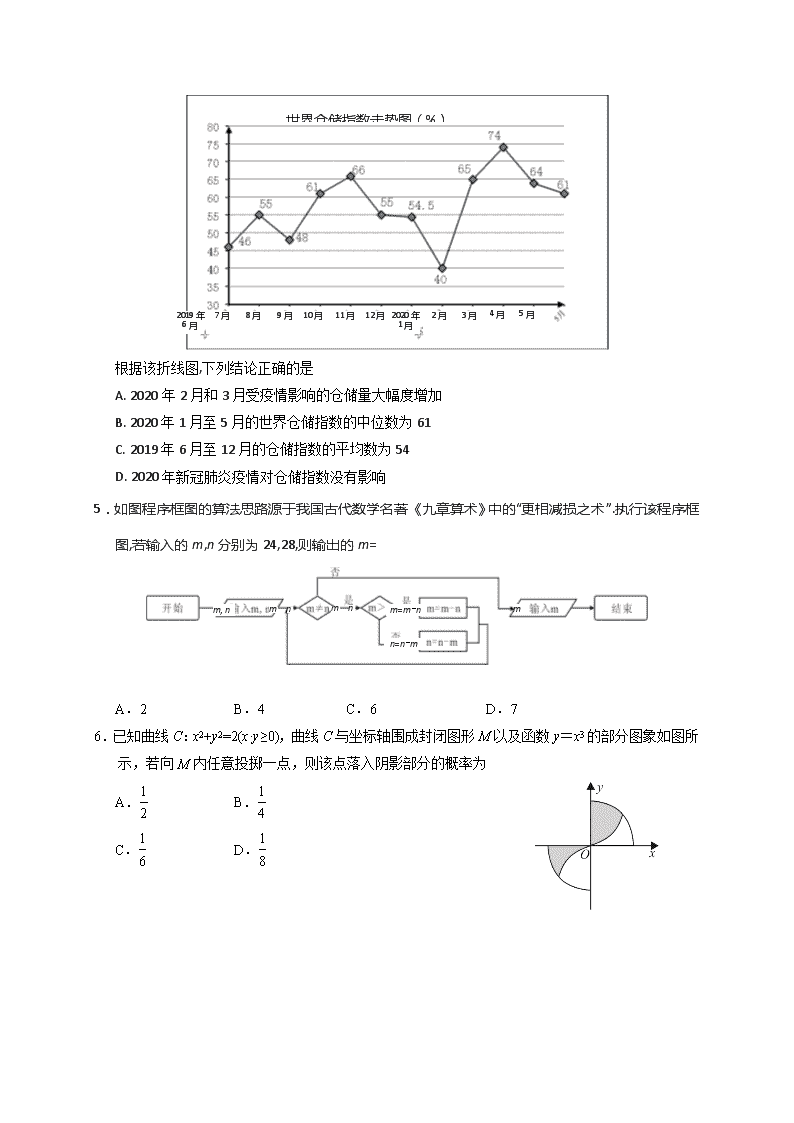‎ ‎2．已知复数满足，则 A． B．1 C． D．2 ‎ ‎3．命题“∀x∈R，x2＋cosx-ex≤1”的否定是 A．∃x∈R ，x2＋cosx-ex>1 B．∃x∈R ，x2＋cosx-ex≥1‎ C．∀x∈R，x2＋cosx-ex≤1 D．∀x∈R，x2＋cosx-ex<1‎ ‎4．2020年初世界各地相继爆发了“新冠肺炎”疫情，随着疫情持续蔓延，各国经济发展受到巨大影响，特别是仓储物流等行业面临前所未有的严峻考验。世界物流与采购联合会为了估计疫情对仓储物流业的影响，针对各行业对仓储物流业需求变化以及商品库存变化开展调研，制定了世界仓储指数。由2019年6月至2020年5月的调查数据得出的世界仓储指数,绘制出如下的折线图. ‎ 世界仓储指数走势图（%）‎ ‎2019年 ‎6月 ‎ 7月 ‎ 8月 ‎ 9月 ‎ 10月 ‎ 11月 ‎ 12月 ‎2020年 ‎1月 ‎ 2月 ‎ 3月 ‎ 4月 ‎ 5月 根据该折线图,下列结论正确的是 A. 2020年2月和3月受疫情影响的仓储量大幅度增加 B. 2020年1月至5月的世界仓储指数的中位数为61‎ C. 2019年6月至12月的仓储指数的平均数为54‎ D. 2020年新冠肺炎疫情对仓储指数没有影响 ‎5．如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损之术”.执行该程序框图,若输入的m,n分别为24,28,则输出的m= ‎ m, n m=m-n n=n-m m n m m n A．2 B．4 C．6 D．7‎ ‎6．已知曲线C：x2+y2=2(x·y≥0)，曲线C与坐标轴围成封闭图形M以及函数y＝x3的部分图象如图所示，若向M内任意投掷一点，则该点落入阴影部分的概率为 A． B． C． D． ‎7．函数f(x)= , a=70.5, b=log0.50.7, c=log0.75, 则 A．f(a)0)的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0,2)，则C的标准方程为 A．y2＝4x或y2＝8x B．y2＝2x或y2＝8x C．y2＝4x或y2＝16x D．y2＝2x或y2＝16x ‎1‎ O y x ‎9．“钱江潮”主要由杭州湾入海口的特殊地形形成，杭州湾外宽内窄，外深内浅，是一个典型的喇叭状海湾。起潮时，宽深的湾口，一下子吞进大量海水，由于江面迅速收缩变窄变浅，夺路上涌的潮水来不及均匀上升，便都后浪推前浪，一浪更比一浪高。诗云:"钱塘一望浪波连,顷刻狂澜横眼前;看似平常江水里,蕴藏能量可惊天。"观测员在某观测点观察潮水的高度时，发现潮水高度(y)随时间(x)的变化可近似看成函数y=cos(wx+φ)，现已知在某观测点测得部分函数图像如图所示，则此函数的单调递减区间为 ‎ A．(kp+, kp+),kÎZ ‎ B．(2kp-,2kp+),kÎZ ‎ C．(k-, k+),kÎZ ‎ D．(2k-, 2k+),kÎZ ‎10. 在三棱锥中，是边长为3的正三角形，BD⊥平面ABC且BD=4，则该三棱锥的外接球的体积为 A．28π B．28π C．π D．π ‎(‎ ‎11. 已知扇形AOB中∠AOB=，点C为弧AB上任意一点（不含点A，B），‎ 若=l+μ,(l,μ∈R), 则l+μ的取值范围是 A．(,1) B．(1,2] C．(1,2) D．(,]‎ ‎12. 设函数f(x)是定义在(0,+∞)上的单调函数，且对于任意正数x,y均有f(xy)=f(x)+f(y)，已知f(2)=1，若一个各项均为正数的数列{an}满足f(Sn)=f(an)+f(an+1)-1(n∈N*)，其中Sn是数列的前n 项和，令bn = ，数列{bn}的前n项和为Tn,则T2020的值为 A．2020 B． C． D． 第Ⅱ卷（非选择题，共90分）‎ 二、填空题：本大题共4个小题,每小题5分，共20分.‎ ‎13．现有钉钉、腾讯、伯索云、直播云、云视讯5种在线教学软件，若某学校要从中随机选取2种作为教师“停课不停学”的教学工具，则被选取的软件中含钉钉概率为 .‎ ‎14. 已知函数满足，且，则 .‎ ‎15．已知函数，方程有三个不同的实数根，则a的取值范围是 . ‎ ‎16．定义：数列{an},{bn}满足= ,则称数列{bn}为{an}的“友好数列”.若数列{an}的通项公式an=3n+1，n∈N*，则数列{an}的“友好数列”{bn}的通项公式为 ；记数列{bn-tn}的前n项和为Sn,且Sn≤S6，则t的取值范围是 . （本小题第一空2分，第二空3分）‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.‎ ‎17．（本小题满分12分）‎ 随着电商事业的快速发展，网络购物交易额也快速提升。特别是每年的双十一天猫的交易额数目惊人。2019年天猫公司的工作人员为了迎接"淘宝天猫双十一年度购买狂欢节"加班加点做了很多准备活动，经过一天的忙碌，截止到2019年11月11日24时，2019年的天猫双11交易额定格在2600亿元，比2018年双十一总成交额超出500多亿元。天猫总公司所有员工对于新的战绩皆大欢喜，同时又对2020年充满了憧憬，因此 公司工作人员反思从2013年至2019年每年双十一总交易额（此处取近似值），进行分析统计如下表：‎ 年份 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ ‎2019‎ 总交易额（近似值）单位（百亿）‎ ‎3.5‎ ‎5.7‎ ‎9.1‎ ‎12‎ ‎17‎ ‎21.2‎ ‎26‎ 可能用到的数据：(xi-)(yi-)=106.4，(xi-)2=28‎ 参考公式： = = ,=- ‎（1）已知年份x与年总交易额y具有线性相关关系，利用最小二乘法求出总交易额与年份之间回归直线方程；‎ ‎（2）估计2020年天猫双十一的总交易额会达到多少？.‎ ‎18．（本小题满分12分）‎ 在中，内角A,B,C所对的边分别为a,b,c.已知且B为锐角.‎ ‎（1）求sinB;‎ ‎（2）若且面积为，当a>c时，求a+b的值.‎ ‎19. （本小题满分12分）‎ 如图，在三棱柱中，平面平面，四边形是正方形，点是棱的中点，点E是线段BB1上一点，，，．‎ ‎（1）求证：；‎ ‎（2）求三棱锥E-ADC1体积的最大值.‎ ‎ ‎ ‎20.（本小题满分12分） ‎ 已知椭圆的左焦点为，且经过点，A,B分别是G的右顶点和上顶点，过原点的直线与G交于两点（点在第一象限），且与线段交于点 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎ ‎. ‎ ‎（1）求椭圆G的标准方程；‎ ‎（2）若的面积是的面积的倍，求直线的方程.‎ ‎21．（本小题满分12分）‎ 已知函数f(x)=ex-a(1+) (a≥0).‎ ‎（1）当a=1时，求f(x)在x=1处的切线方程；‎ ‎（2）若f(x)≥恒成立，求实数a的取值范围.‎ 请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分。做答时请写清题号。‎ ‎22．[选修4－4：坐标系与参数方程]（10分）‎ 在极坐标系中，O为极点，曲线与直线的除极点外的交点为A，直线l2过点且与OA垂直，垂足为M．‎ ‎（1）当A与M重合时，求A点的极坐标及l2的极坐标方程；‎ ‎（2）当点A为曲线C上动点且M在线段OA的延长线上时，求M点轨迹的极坐标方程．‎ ‎23． [选修4—5：不等式选讲]（10分）‎ 设函数．‎ ‎（1）画出的图像；‎ ‎（2）当， 有两个不同的实数根，求a的取值范围．‎ 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎ ‎2020年葫芦岛市普通高中高三第二次模拟考试 数学（文）参考答案及评分标准 一、选择题：1-5 ：CCAAB 6-10：ADCDC 11-12 BD 二、填空题：13. 14. 8 15. 0c得 ‎ ……………………………………………………………………………8‎ 由（1）知，所以 ‎ …………………………………………………………………………………10‎ 所以 ……………………………………………………………………12‎ ‎（本题仅提供一种方法，采用其他方法亦赋分）‎ ‎20.解：（Ⅰ）法一：依题意可得解得 所以椭圆的标准方程为. ……………………………………………6‎ 法二：设椭圆的右焦点为，则，‎ 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎ ‎，‎ ‎， ，‎ 所以椭圆的标准方程为. ……………………………………………6‎ ‎（2）设，，则，易知，.‎ 由，，所以直线的方程为. ………………8‎ ‎ 若使的面积是的面积的4倍，只需使得， ‎ 法一：即 ① . ‎ 设直线的方程为，由 得， ……10‎ 由 得，， …13分 代入①可得，即：‎ 解得，所以. …………………………………………12‎ 法二：所以，即. …………………………8‎ 设直线的方程为，由 得， ‎ 所以………………………………………………………10‎ 因为点在椭圆上，所以， ‎ 代入可得，即：‎ 解得，所以. ………………………………………12‎ 法三：所以，即. …………………………8‎ 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎ 点在线段上，所以，整理得，-----① ‎ 因为点在椭圆上，所以，------② ‎ 把①式代入②式可得，解得. ………………10‎ 于是，所以，.‎ 所以，所求直线的方程为. ……………………………………12‎ ‎21.解：（1）a=1时，f(x)= ex-1- ，………………………………………………2‎ ‎ f¢(x)=ex- ∴f¢(1)=e-1,f(1)=e-1 …………………………………………………4‎ 所以切线方程为：y-(e-1)=(e-1)(x-1) 即：y=(e-1)x ………………………………6‎ ‎(2) 法一：f(x)≥Ûxex-a(x+lnx)-1≥0 令t(x)= xex-a(x+lnx)-1≥0 则t¢(x)= a=0时，t(x)=xex，显然不合题意；……………………………………………………8‎ a>0时，令j(x)=xex-a,则显然j(x)在(0，+¥)上单调递增，j(0)=-a<0, j(a)=aea-a>0,故存在唯一x0Î(0,+¥),使得j(x0)=0,即：x0ex0=a,lnx0+x0=lna 当xÎ(0,x0)时，j(x)<0即t¢(x)<0,当xÎ(x0,+¥)时，j(x)>0即t¢(x)>0,‎ ‎∴t(x)在(0,x0)单调递减，在(x0,+¥)单调递增，………………………………………10‎ ‎∴tmin(x)=t(x0)= x0ex0-a(x0+lnx0)-1≥0‎ 即：a-alna-1≥0 令h(a)= a-alna-1,h¢(a)=-lna, ‎ ‎∴h(a)在（0，1）递增，在（1，+¥）上递减 ‎∴h(a)≤h(1)=0 ∴h(a)=0,即a=1,综上,a的取值范围为{1};…………………………12‎ 法二：f(x)≥Ûxex-a(x+lnx)-1≥0Ûex+lnx-a(x+lnx)-1≥0,令t=x+lnxÎR,h(t)=et-at-1‎ 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎ 则h¢(t)=et-a, hmin(t)=h(lna)=a-alna-1 ∴a-alna-1≥0 以下同法一。（此法亦赋分）‎ ‎…………5‎ 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎ 高三数学（文）试卷 第6页 （共6页）‎ 高三数学（文）试卷 第5页 （共6页）‎