高中数学必修2教案：平面与平面垂直的性质 4页

课时41 平面与平面垂直的性质 一、选择题 ‎1. 二面角－l－是直二面角，a ∈ ，b∈，且a、b与l都是斜交，那么 ( D )‎ A. a与b可能垂直，但不可能平行． B. a与b可能垂直，也可能平行．‎ C.a与b不可能垂直，但可能平行． D. a与b不可能平行，也不可能垂直．‎ ‎2. 在下列关于直线l、m与平面α、β的命题中,真命题是 ( B )‎ A.若lβ且α⊥β,则l⊥α. B. 若l⊥β且α∥β,则l⊥α.‎ C.若l⊥β且α⊥β,则l∥α. D. 若α∩β=m且l∥m,则l∥α.‎ ‎3. 在互相垂直的两个平面中，下列命题中①一个平面内的已知直线必垂直于另一个平面内的任意一条直线；②一个平面内的已知直线必垂直于另一个平面内的无数条直线；③一个平面内的任意一直线必垂直于另一个平面内的无数条直线；④过一个平面内的任意一点作垂直于另一个平面的直线必在第一个平面内；正确的个数是 （ C ）‎ ‎ A．1 B．‎2 C．3 D．4‎ ‎4.下列四个命题中错误的一个是 （ D ）‎ A．空间存在不共面的四个点A、B、C、D，如果AB⊥CD，AD⊥BC，则AC⊥BD；‎ B．若lβ，且l⊥α，则α⊥β；‎ C．若α，β，γ是三个不同的平面，a 表示直线，如果α∩β=a,α⊥γ,β⊥γ，则a⊥γ；‎ D．与两条异面直线都垂直的直线是这两条异面直线的公垂线 ‎5. 关于直线l，m，n以及平面，下列命题中正确的是 （ D ）‎ ‎ A．若 B．若 C．若 D．若 二、填空题 ‎6. 设有不同的直线、和不同的平面、、，给出下列三个命题：‎ ‎（1）若，，则．（2）若，，则．‎ ‎（3）若，，则． 其中正确的个数是 ‎ ‎7. 设P是的二面角内一点，垂足，则AB的长为 . ‎ ‎8. 、是两个不同的平面，m、n是平面、之外的两条不同的直线，给出四个论断：‎ ‎ ①m⊥n，②⊥，③n⊥，④m⊥，以其中三个论断作为条件，余下一个论断 ‎ 作为结论，写出你认为正确的一个命题 ．‎ ‎9. 已知m、n是直线，是平面，给出下列命题（1）若，，则（2）若则（3）若内不共线三点 A，B，C到的距离都相等，则（4）若且（5）若m,n为异面直线，且. 则其中正确的是 .‎ ‎10. 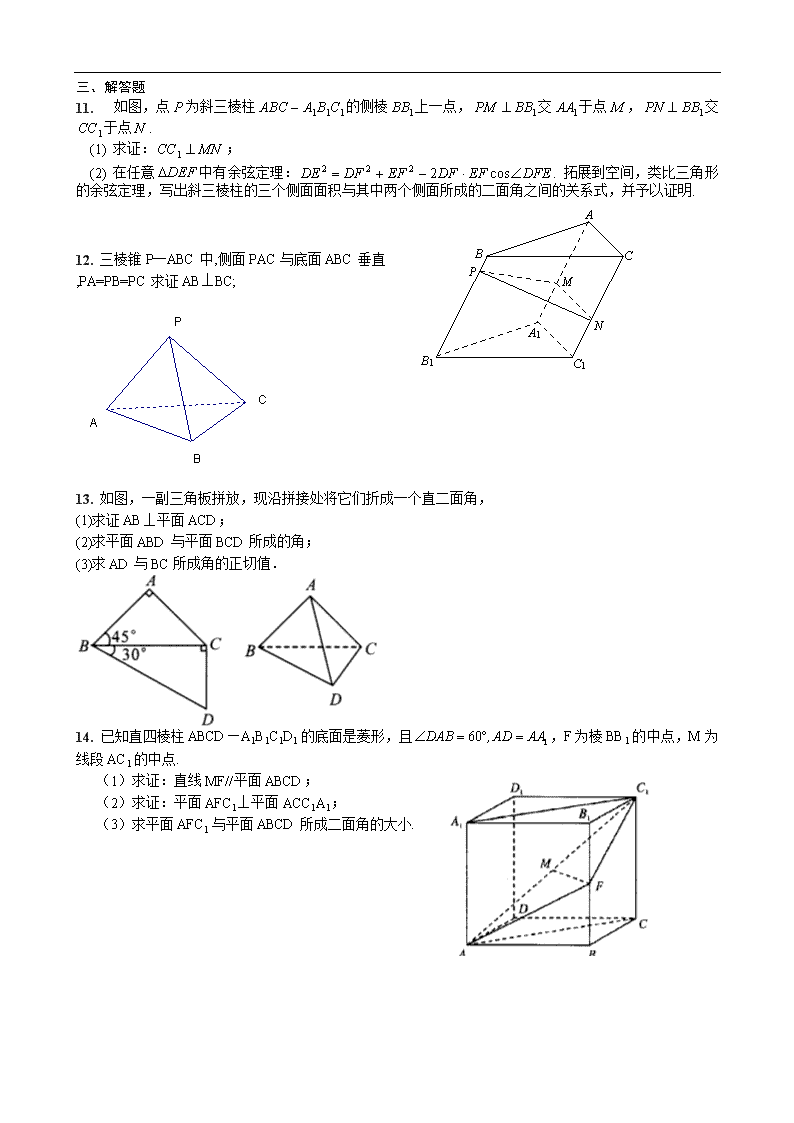已知平面α和平面交于直线，P是空间一点，PA⊥α，垂足为A，PB⊥β，垂足为B，且PA=1，PB=2，若点A在β内的射影与点B在α内的射影重合，则点P到的距离为 .‎ 三、解答题 ‎11. 如图，点为斜三棱柱的侧棱上一点，交于点，交于点.‎ ‎ (1) 求证：；‎ ‎ (2) 在任意中有余弦定理：. 拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明.‎ A A1‎ B1‎ B C1‎ C M N P ‎12. 三棱锥P─ABC中,侧面PAC与底面ABC垂直 ‎,PA=PB=PC求证AB⊥BC;‎ ‎13. 如图，一副三角板拼放，现沿拼接处将它们折成一个直二面角，‎ ‎(1)求证AB⊥平面ACD；‎ ‎(2)求平面ABD与平面BCD所成的角；‎ ‎(3)求AD与BC所成角的正切值．‎ ‎14. 已知直四棱柱ABCD—A1B‎1C1D1的底面是菱形，且，F为棱BB1的中点，M为线段AC1的中点.‎ ‎ （1）求证：直线MF//平面ABCD；‎ ‎ （2）求证：平面AFC1⊥平面ACC‎1A1；‎ ‎ （3）求平面AFC1与平面ABCD所成二面角的大小.‎ ‎【课时41答案】‎ ‎1.D 2.B 3.C 4.D 5. D ‎6.0.‎ ‎7. 设平面PAB交棱l于点Q，则由PA⊥平面α，PB⊥平面β知：l⊥PA，l⊥PB．‎ 于是∠AQB为二面角α－l—β的平面角，从而∠AQB=60°，故∠APB=1 20°．‎ 在△APB中，AB 2=PA 2 ＋PB 2—2 PA·PB cos 1 20°=28．．‎ ‎8. ②、③、④ ① 或 ①、③、④ ② 9. （2）（5） 10.‎ ‎11. (1) 证：；‎ ‎ (2) 解：在斜三棱柱中，有，其中为 ‎ 平面与平面所组成的二面角. ‎ 上述的二面角为,在中，‎ ‎，‎ ‎ 由于，‎ ‎ 有.‎ ‎12. 如图,取AC中点D,连结PD、BD.‎ 因为PA=PC,所以PD⊥AC,‎ 又已知面PAC⊥面ABC.‎ 所以PD⊥面ABC,D为垂足.‎ 因为PA=PB=PC,‎ 所以DA=DB=DC,可知AC为ΔABC的外接圆直径,‎ 因此AB⊥BC.‎ ‎13. (1)∵CD⊥BC，平面ABC⊥平面BCD,CD⊥平面ABC，CD⊥AB, 又∵AB⊥AC,AB⊥平面ACD．‎ ‎(2)过A作AE⊥BC于E．∵平面ABC⊥平面BCD．∴AE⊥平面BCD．过E作EF⊥BD于F，连结AF．得AF⊥ BD ∴∠AFE就是平面ABD与平面BCD所成二面角的平面 ‎ ‎14.（Ⅰ）延长C‎1F交CB的延长线于点N，连结AN.因为F是BB1的中点，‎ 所以F为C1N的中点，B为CN的中点.‎ 又M是线段AC1的中点，故MF//AN.‎ ‎ ‎ ‎（Ⅱ）证明：连BD，由直四棱柱ABCD—A1B1C1D1‎ 可知：平面ABCD, ‎ 又∵BD平面ABCD， ‎ 四边形ABCD为菱形，‎ ‎ ‎ 在四边形DANB中，DA∥BN且DA=BN，所以四边形DANB为平行四边形.‎ 故NA∥BD，平面ACC1A1. ‎ ACC‎1A1. ‎ ‎（Ⅲ）由（Ⅱ）知BD⊥ACC1A1，又AC1 ACC1A1，‎ ‎ ∴BD⊥AC1，∵BD//NA，∴AC1⊥NA.‎ ‎ 又由BD⊥AC可知NA⊥AC，‎ ‎∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角. ‎ 在Rt△C1AC中，， ‎ 故∠C1AC=30°.‎ ‎∴平面AFC1与平面ABCD所成二面角的大小为30°或150°.‎