高中数学必修2教案：第二章 2_3_3-2_3_4平面与平面垂直的性质 15页

‎2．3.3　直线与平面垂直的性质 ‎2．3.4　平面与平面垂直的性质 ‎[学习目标]　1.理解直线和平面垂直、平面与平面垂直的性质定理，并能用文字、符号和图形语言描述定理.2.会用线面垂直、面面垂直的性质定理证明相关问题.3.理解“平行”与“垂直”之间的相互转化．‎ ‎[知识链接]‎ ‎1．线面垂直的判定定理：若一条直线垂直于平面内的两条相交直线，则该直线与此平面垂直．‎ ‎2．面面垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直．‎ ‎[预习导引]‎ ‎1．直线与平面垂直的性质定理 文字语言 垂直于同一个平面的两条直线平行 符号语言 ⇒a∥b 图形语言 作用 ‎①线面垂直⇒线线平行②作平行线 ‎2.平面与平面垂直的性质定理 文字语言 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直 符号语言 ⇒a⊥β 图形语言 作用 ‎①面面垂直⇒线面垂直 ‎②作面的垂线 要点一　直线与平面垂直的性质及应用 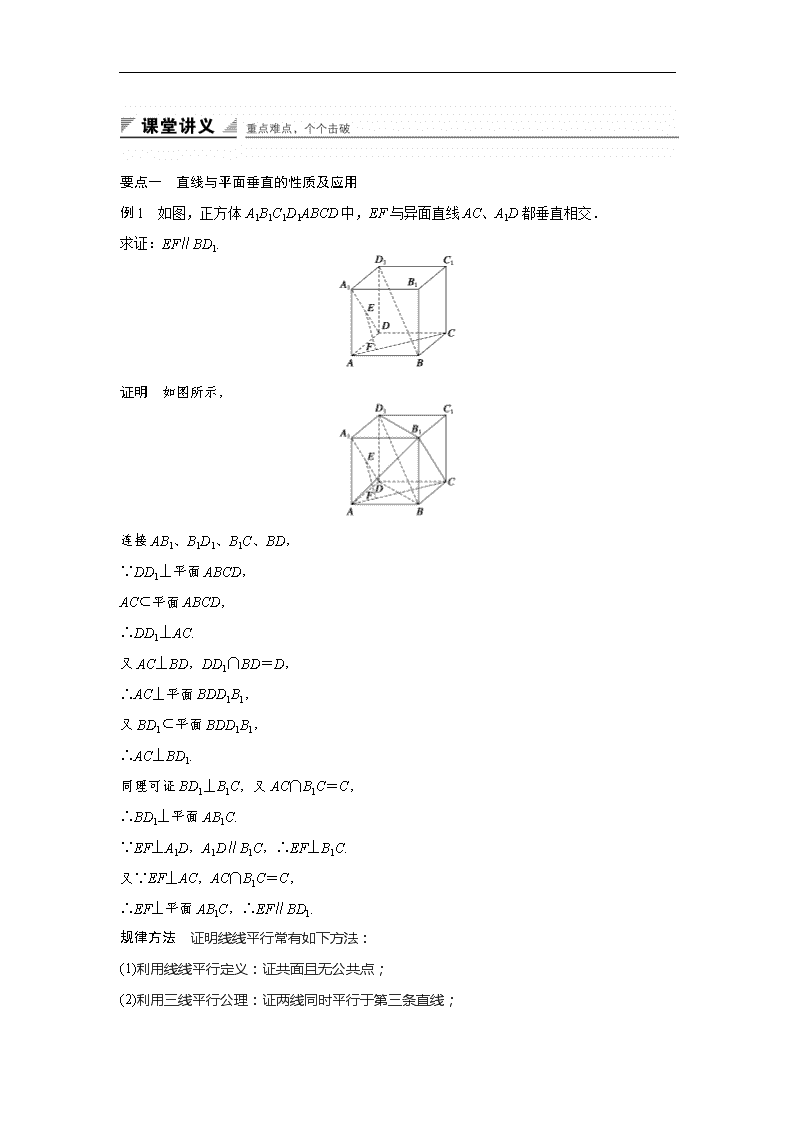例1　如图，正方体A1B1C1D1ABCD中，EF与异面直线AC、A1D都垂直相交．‎ 求证：EF∥BD1.‎ 证明　如图所示，‎ 连接AB1、B1D1、B1C、BD，‎ ‎∵DD1⊥平面ABCD，‎ AC⊂平面ABCD，‎ ‎∴DD1⊥AC.‎ 又AC⊥BD，DD1∩BD＝D，‎ ‎∴AC⊥平面BDD1B1，‎ 又BD1⊂平面BDD1B1，‎ ‎∴AC⊥BD1.‎ 同理可证BD1⊥B1C，又AC∩B1C＝C，‎ ‎∴BD1⊥平面AB1C.‎ ‎∵EF⊥A1D，A1D∥B1C，∴EF⊥B1C.‎ 又∵EF⊥AC，AC∩B1C＝C，‎ ‎∴EF⊥平面AB1C，∴EF∥BD1.‎ 规律方法　证明线线平行常有如下方法：‎ ‎(1)利用线线平行定义：证共面且无公共点；‎ ‎(2)利用三线平行公理：证两线同时平行于第三条直线；‎ ‎(3)利用线面平行的性质定理：把证线线平行转化为证线面平行；‎ ‎(4)利用线面垂直的性质定理：把证线线平行转化为证线面垂直；‎ ‎(5)利用面面平行的性质定理：把证线线平行转化为证面面平行．‎ 跟踪演练1　如图，已知平面α∩平面β＝l，EA⊥α，垂足为A，EB⊥β，垂足为B，直线a⊂β，a⊥AB.求证：a∥l.‎ 证明　因为EA⊥α，α∩β＝l，即l⊂α，所以l⊥EA.‎ 同理l⊥EB，又EA∩EB＝E，所以l⊥平面EAB.‎ 因为EB⊥β，a⊂β，‎ 所以EB⊥a，‎ 又a⊥AB，EB∩AB＝B，‎ 所以a⊥平面EAB.因此，a∥l.‎ 要点二　平面与平面垂直的性质及应用 例2　已知：α、β、γ是三个不同平面，l为直线，α⊥γ，β⊥γ，α∩β＝l.求证：l⊥γ.‎ 证明　方法一　设α∩γ＝a，β∩γ＝b，在γ内任取一点P，过P在γ内作直线m⊥a，n⊥b，如图．‎ ‎∵α⊥γ，β⊥γ，∴m⊥α，n⊥β，‎ 又∵α∩β＝l，‎ ‎∴m⊥l，n⊥l，又m∩n＝P，∴l⊥γ.‎ 方法二　如图，α∩γ＝a，‎ β∩γ＝b，在α内作m⊥a，‎ 在β内作n⊥b.‎ ‎∵α⊥γ，β⊥γ，∴m⊥γ，n⊥γ，‎ ‎∴m∥n.‎ 又∵n⊂β，m⊄β，∴m∥β，‎ 又α∩β＝l，m⊂α，∴m∥l，∴l⊥γ.‎ 规律方法　1.证明或判定线面垂直的常用方法：‎ ‎(1)线面垂直的判定定理；‎ ‎(2)面面垂直的性质定理；‎ ‎(3)若a∥b，a⊥α则b⊥α；(a，b为直线，α为平面)．‎ ‎(4)若a⊥α，α∥β则a⊥β；(a为直线，α，β为平面)．‎ ‎2．两平面垂直的性质定理告诉我们要将面面垂直转化为线面垂直，方法是在其中一个面内作(找)与交线垂直的直线．‎ 跟踪演练2　设平面α⊥平面β，点P在平面α内，过点P作平面β的垂线a，试判断直线a与平面α的位置关系．‎ 解　如图，设α∩β＝c，过点P在平面α内作直线b⊥c，‎ 根据平面与平面垂直的性质定理有b⊥β.‎ 因为过一点有且只有一条直线与平面β垂直，‎ 所以直线a与直线b重合，‎ 因此a⊂α.‎ 要点三　线线、线面、面面垂直的综合应用 例3　如图所示，在四棱锥PABCD中，底面ABCD是边长为a的菱形，且∠DAB＝60°，侧面PAD为正三角形，其所在的平面垂直于底面ABCD.‎ ‎(1)若G为AD边的中点，求证：BG⊥平面PAD；‎ ‎(2)求证：AD⊥PB.‎ 证明　(1)∵在菱形ABCD中，‎ G为AD的中点，∠DAB＝60°，∴BG⊥AD.‎ 又平面PAD⊥平面ABCD，‎ 平面PAD∩平面ABCD＝AD，∴BG⊥平面PAD.‎ ‎(2) 连接PG，如图，‎ ‎∵△PAD为正三角形，‎ G为AD的中点，∴PG⊥AD.‎ 由(1)知BG⊥AD，PG∩BG＝G，‎ ‎∴AD⊥平面PGB，‎ ‎∵PB⊂平面PGB，∴AD⊥PB.‎ 规律方法　证明线面垂直，一种方法是利用线面垂直的判定定理，另一种方法是利用面面垂直的性质定理．本题已知面面垂直，故可考虑面面垂直的性质定理．利用面面垂直的性质定理．证明线面垂直的问题时，要注意以下三点：(1)两个平面垂直；(2)直线必须在其中一个平面内；(3)直线必须垂直于它们的交线．‎ 跟踪演练3　如图，已知四棱锥PABCD的底面是直角梯形，∠ABC＝∠BCD＝90°，AB＝BC＝PB＝PC＝2CD，侧面PBC⊥底面ABCD.PA与BD是否相互垂直？请证明你的结论．‎ 解　PA与BD相互垂直．证明过程如下：‎ 如图，取BC的中点O，连接PO、AO.‎ ‎∵PB＝PC，‎ ‎∴PO⊥BC，‎ 又侧面PBC⊥底面ABCD，‎ ‎∴PO⊥底面ABCD，又BD⊂平面ABCD.‎ ‎∴PO⊥BD，‎ 在直角梯形ABCD中，易证△ABO ≌△BCD，‎ ‎∠BAO＝∠CBD，∠CBD＋∠ABD＝90°，‎ ‎∴∠BAO＋∠ABD＝90°，∴AO⊥BD，‎ 又PO∩AO＝O，∴BD⊥平面PAO，∴BD⊥PA，‎ 即PA与BD相互垂直.‎ ‎1．下列说法正确的是(　　)‎ A．垂直于同一条直线的两直线平行 B．垂直于同一条直线的两直线垂直 C．垂直于同一个平面的两直线平行 D．垂直于同一条直线的一条直线和平面平行 答案　C 解析　由线面垂直的性质定理知C正确．‎ ‎2．△ABC所在的平面为α，直线l⊥AB，l⊥AC，直线m⊥BC，m⊥AC，则直线l，m的位置关系是(　　)‎ A．相交 B．异面 C．平行 D．不确定 答案　C 解析　因为l⊥AB，l⊥AC，AB⊂α，AC⊂α且AB∩AC＝A，所以l⊥α，同理可证m⊥α，所以l∥m.‎ ‎3．设αlβ是直二面角，直线a⊂α，直线b⊂β，a，b与l都不垂直，那么(　　)‎ A．a与b可能垂直，但不可能平行 B．a与b可能垂直，也可能平行 C．a与b不可能垂直，但可能平行 D．a与b不可能垂直，也不可能平行 答案　C 解析　当a，b都与l平行时，‎ 则a∥b，所以A、D错，‎ 如图，若a⊥b，过a上一点P在α内作a′⊥l，‎ 因为α⊥β，所以a′⊥β，‎ 又b⊂β，∴a′⊥b，∴b⊥α，‎ 而l⊂α，∴b⊥l，与b和l不垂直矛盾，所以B错．‎ ‎4．已知a、b为直线，α、β为平面．在下列四个命题中，正确的命题是________．‎ ‎①若a⊥α，b⊥α，则a∥b；②若a∥α，b∥α，则a∥b；③若a⊥α，a⊥β，则α∥β；④若α∥b，β∥b，则α∥β.‎ 答案　①③‎ 解析　由“垂直于同一平面的两直线平行”知①真；由“平行于同一平面的两直线平行或异面或相交”知②假；由“垂直于同一直线的两平面平行”知③真；易知④假．‎ ‎5. 如图，在三棱锥PABC内，侧面PAC⊥底面ABC，且∠PAC＝90°，PA＝1，AB＝2，则PB＝________.‎ 答案　 解析　∵侧面PAC⊥底面ABC，交线为AC，∠PAC＝90°(即PA⊥AC)，‎ ‎∴PA⊥平面ABC，‎ ‎∴PA⊥AB，∴PB＝＝＝.‎ ‎1.线面垂直的性质定理揭示了空间中“平行”与“垂直”关系的内在联系，提供了“垂直”与“平行”关系相互转化的依据．‎ ‎2．面面垂直的性质定理揭示了“面面垂直、线面垂直及线线垂直”间的内在联系，体现了数学中的转化与化归思想，其转化关系如下：‎ 一、基础达标 ‎1．下列命题中错误的是(　　)‎ A．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β B．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β C．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥平面γ D．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β 答案　D 解析　由平面与平面垂直的有关性质可以判断出D项错误．‎ ‎2．在长方体ABCDA1B1C1D1的棱AB上任取一点E，作EF⊥A1B1于F，则EF与平面A1B1C1D1的关系是(　　)‎ A．平行 B．EF⊂平面A1B1C1D1‎ C．相交但不垂直 D．相交且垂直 答案　D 解析　在长方体ABCDA1B1C1D1中，平面A1ABB1⊥平面A1B1C1D1且平面A1ABB1∩平面A1B1C1D1＝A1B1，又EF⊂面A1ABB1，EF⊥A1B1，∴EF⊥平面A1B1C1D1，答案D正确．‎ ‎3．如图所示，三棱锥PABC中，平面ABC⊥平面PAB，PA＝PB，AD＝DB，则(　　)‎ A．PD⊂平面ABC B．PD⊥平面ABC C．PD与平面ABC相交但不垂直 D．PD∥平面ABC 答案　B 解析　∵PA＝PB，AD＝DB，‎ ‎∴PD⊥AB.‎ 又∵平面ABC⊥平面PAB，‎ 平面ABC∩平面PAB＝AB，‎ ‎∴PD⊥平面ABC.‎ ‎4. 如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥ABCD，则在三棱锥ABCD中，下列命题正确的是(　　)‎ A．平面ABD⊥平面ABC B．平面ADC⊥平面BDC C．平面ABC⊥平面BDC D．平面ADC⊥平面ABC 答案　D 解析　如图，在平面图形中CD⊥BD，折起后仍然满足CD⊥BD，由于平面ABD⊥平面BCD，故CD⊥平面ABD，CD⊥AB.又AB⊥AD，故AB⊥平面ADC，又AB⊂平面ABC，所以平面ADC⊥平面ABC.‎ ‎5．设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是(　　)‎ A．若α⊥β，m⊂α，n⊂β，则m⊥n B．若α∥β，m⊂α，n⊂β，则m∥n C．若m⊥n，m⊂α，n⊂β，则α⊥β D．若m⊥α，m∥n，n∥β，则α⊥β 答案　D 解析　如图，在长方体ABCDA1B1C1D1中，平面BCC1B1⊥平面ABCD，BC1⊂平面BCC1B1，BC⊂平面ABCD，而BC1不垂直于BC，故A错误．‎ 平面A1B1C1D1∥平面ABCD，B1D1⊂平面A1B1C1D1，‎ AC⊂平面ABCD，但B1D1和AC不平行，故B错误．‎ AB⊥A1D1，AB⊂平面ABCD，A1D1⊂平面A1B1C1D1，但平面A1B1C1D1∥平面ABCD，故C错误．故选D.‎ ‎6．如图，边长为2a的正△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，现给出下列结论，其中正确的结论有________．(填上所有正确结论的序号)‎ ‎①动点A′在平面ABC上的射影在线段AF上．‎ ‎②三棱锥A′－FED的体积有最大值．‎ ‎③恒有平面A′GF⊥平面BCED.‎ ‎④异面直线A′E与BD不可能互相垂直．‎ 答案　①②③‎ 解析　因为DE⊥A′G，DE⊥GF，A′G ∩GF＝G，‎ 所以DE⊥平面A′GF，‎ 又DE⊂平面BCED，‎ 所以平面A′GF⊥平面BCED，故③正确．‎ 过A′作A′H⊥AF，垂足为H，‎ 则A′H⊂平面A′GF，‎ 所以A′H⊥DE，又DE∩AF＝G，‎ 所以A′H⊥平面ABC，故①正确．‎ 三棱锥A′－FED的底面△FED的面积是定值，高是点A′到平面FED的距离．‎ 易证当A′G⊥平面FED时距离(即高)最大，三棱锥A′－FED的体积最大，故②正确．‎ 易知BD∥EF，所以∠A′EF是异面直线A′E与BD所成的角．正△ABC的边长为2a，AE＝a，EF＝a，‎ 而A′F的长度的取值范围是(0，a)，‎ 当A′F＝a时，A′E2＋EF2＝A′F2，∠A′EF＝90°，‎ 此时直线A′E与BD互相垂直，故④错误．‎ ‎7. 如图三棱锥PABC中，已知△ABC是等腰直角三角形，∠ABC＝90°，△PAC是直角三角形，∠PAC＝90°，∠ACP＝30°，平面PAC⊥平面ABC.求证：平面PAB⊥平面PBC.‎ 证明　∵平面PAC⊥平面ABC，‎ 平面PAC∩平面ABC＝AC，PA⊥AC，‎ ‎∴PA⊥平面ABC.‎ 又BC⊂平面ABC，‎ ‎∴PA⊥BC.‎ 又AB⊥BC，AB∩PA＝A，‎ ‎∴BC⊥平面PAB.‎ 又BC⊂平面PBC，‎ ‎∴平面PAB⊥平面PBC.‎ 二、能力提升 ‎8. 如图所示，在斜三棱柱ABCA1B1C1中，∠BAC＝90°，BC1⊥AC，则点C1在底面ABC上的投影H必在(　　)‎ A．直线AB上 B．直线BC上 C．直线AC上 D．△ABC内部 答案　A 解析　连接AC1，∠BAC＝90°，即AC⊥AB，又AC⊥BC1，AB∩BC1＝B，所以AC⊥平面ABC1.又AC⊂平面ABC，于是平面ABC1⊥平面ABC，且AB为交线，因此，点C1在平面ABC上的投影必在直线AB上，故选A.‎ ‎9. 如图，正方形SG1G2G3中，E、F分别是G1G2、G2G3的中点，现在沿SE、SF、EF 把这个正方形折成一个四面体，使G1、G2、G3重合，重合后的点记为G.给出下列关系：‎ ‎①SG⊥平面EFG；②SE⊥平面EFG；③GF⊥SE；④EF⊥平面SEG.其中成立的有(　　)‎ A．①与② B．①与③‎ C．②与③ D．③与④‎ 答案　B 解析　由SG⊥GE，SG⊥GF，得SG⊥平面EFG，排除C、D；若SE⊥平面EFG，则SG∥SE，这与SG∩SE＝S矛盾，排除A，故选B.‎ ‎10．如图所示，已知两个正方形ABCD和DCEF不在同一平面内，M，N分别为AB，DF的中点．若CD＝2，平面ABCD⊥平面DCEF，则线段MN的长等于________．‎ 答案　 解析　取CD的中点G，连接MG，NG.‎ 因为ABCD，DCEF为正方形，且边长为2，‎ 所以MG⊥CD，MG＝2，NG＝.‎ 因为平面ABCD⊥平面DCEF，‎ 所以MG⊥平面DCEF，可得MG⊥NG，‎ 所以MN＝＝.‎ ‎11．如图，在四棱锥PABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：‎ ‎(1)PA⊥底面ABCD；‎ ‎(2)BE∥平面PAD；‎ ‎(3)平面BEF⊥平面PCD.‎ 证明　(1)因为平面PAD⊥底面ABCD，‎ 且PA垂直于这两个平面的交线AD，‎ 所以PA⊥底面ABCD.‎ ‎(2)因为AB∥CD，CD＝2AB，‎ E为CD的中点，‎ 所以AB∥DE，且AB＝DE.‎ 所以四边形ABED为平行四边形．‎ 所以BE∥AD.‎ 又因为BE⊄平面PAD，‎ AD⊂平面PAD，‎ 所以BE∥平面PAD.‎ ‎(3)因为AB⊥AD，而且四边形ABED为平行四边形，‎ 所以BE⊥CD，AD⊥CD.‎ 由(1)知PA⊥底面ABCD，‎ 所以PA⊥CD.‎ 所以CD⊥平面PAD.‎ 所以CD⊥PD.‎ 因为E和F分别是CD和PC的中点，‎ 所以PD∥EF.‎ 所以CD⊥EF.‎ 又因为CD⊥BE，EF∩BE＝E，‎ 所以CD⊥平面BEF.‎ 所以平面BEF⊥平面PCD.‎ 三、探究与创新 ‎12．如图所示，在平行四边形ABCD中，已知AD＝2AB＝2a，BD＝a，AC∩BD＝E，将其沿对角线BD折成直二面角．‎ 求证：(1)AB⊥平面BCD；‎ ‎(2)平面ACD⊥平面ABD.‎ 证明　(1)在△ABD中，AB＝a，AD＝2a，BD＝a，‎ ‎∴AB2＋BD2＝AD2，‎ ‎∴∠ABD＝90°，AB⊥BD.‎ 又∵平面ABD⊥平面BCD，‎ 平面ABD∩平面BCD＝BD，AB⊂平面ABD，‎ ‎∴AB⊥平面BCD.‎ ‎(2)∵折叠前四边形ABCD是平行四边形，‎ 且AB⊥BD，‎ ‎∴CD⊥BD.‎ ‎∵AB⊥平面BCD，CD⊂平面BCD.‎ ‎∴AB⊥CD.‎ ‎∵AB∩BD＝B，‎ ‎∴CD⊥平面ABD.‎ 又∵CD⊂平面ACD，‎ ‎∴平面ACD⊥平面ABD.‎ ‎13．在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．‎ ‎(1)若AC⊥BC，证明：直线BC⊥平面ACC1A1；‎ ‎(2)设D，E分别是线段BC，CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．‎ ‎(1)证明　因为四边形ABB1A1和ACC1A1都是矩形，‎ 所以AA1⊥AB，AA1⊥AC.‎ 因为AB，AC为平面ABC内两条相交的直线，‎ 所以AA1⊥平面ABC.‎ 因为直线BC⊂平面ABC，‎ 所以AA1⊥BC.‎ 又由已知，AC⊥BC，AA1，AC为平面ACC1A1内两条相交的直线，所以BC⊥平面ACC1A1.‎ ‎(2)解　取线段AB的中点M，连接A1M，MC，A1C，AC1，设O为A1C，AC1的交点．‎ 由已知，O为AC1的中点．‎ 连接MD，OE，则MD，OE分别为△ABC，△ACC1的中位线，‎ 所以MD綊AC，OE綊AC，‎ 因此MD綊OE.‎ 连接OM，从而四边形MDEO为平行四边形，‎ 则DE∥MO.‎ 因为直线DE⊄平面A1MC，MO⊂平面A1MC，‎ 所以直线DE∥平面A1MC.‎ 即线段AB上存在一点M(线段AB的中点)，使直线DE∥平面A1MC.‎