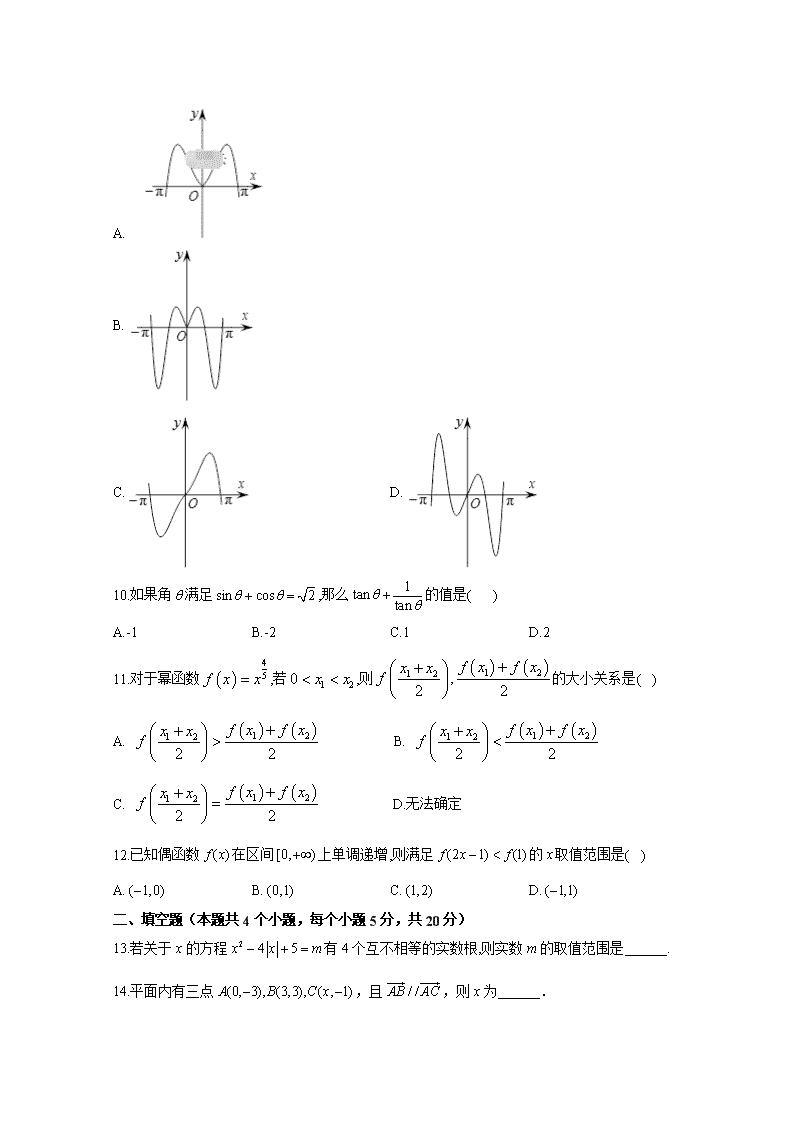2019-2020学年吉林省榆树市第一高级中学高一上学期尖子生第二次考试数学（理）试卷（解析版） 10页

吉林省榆树市第一高级中学 2019-2020 学年高一上学期尖子 生第二次考试数学（理）试卷 总分 150 分 时间 120 分 一、选择题（本题共 12 个小题，每题 5 分，共 60 分） 1.已知集合 ， ，则 ( ) A. B. C. D. 2.已知函数 ，则 的值域是（ ） A． B． C． D． 3.若向量 ,则 （ ） A. B. C. D. 4.已知 ,则 ( ). A. B. C. D. 5.若将函数 的图像向左平移 个单位长度,则平移后图像的一个对称中心可以 为( ) A. B. C. D. 6.设 ,向量 若 ,则 m 等于（ ） A． B． C． D． 7.将函数 的图象上所有点的横坐标伸长到原来的 2 倍(纵坐标不变),再将所得的 图象向左平移 个单位,得到的图象对应的解析式是( ) A. B. C. D. 8.函数 的单调递增区间是（ ） A. B. C. D. 9.函数 的图象可能是( ) 2{ | 4 }A x x x= < { | 2 5}B x x= < < A B = { | 0 2}x x< < { | 4 5}x x< < { | 2 4}x x< < { | 0 5}x x< < 2( ) 2 ( 2 1 )Zf x x x x x= + − ≤ ≤ ∈且 ( )f x [0,3] { }1,0,3− { }0,1,3 [ 1,3]− (1,2), (3,4)AB BC= =  AC = ( )4,6 ( )4, 6− − ( 2, 2)− − ( )2,2 tan 3α = 2 2 2 sin 2cos sin cos sin α α α α α + =+ 3 8 9 16 11 12 7 9 1( ) cos22f x x= π 6 π ,012      π ,06      π ,03      π ,02      Rm∈ (1, 2), ( , 2)a b m m= − = − a b⊥  2 3 − 2 3 4− 4 πsin 3y x = −   π 3 1sin 2y x= 1 πsin 2 6y x = −   1 πsin 2 2y x = −   πsin 2 6y x = −   ( ) ( )2ln 2 8f x x x= − − ( ), 2−∞ − ( 1),−∞ (1, )+∞ (4, )+∞ 2 sin 2xy x= A. B. C. D. 10.如果角 满足 ,那么 的值是( ) A.-1 B.-2 C.1 D.2 11.对于幂函数 ,若 ,则 的大小关系是( ) A. B. C. D.无法确定 12.已知偶函数 在区间 上单调递增,则满足 的 取值范围是( ) A. B. C. D. 二、填空题（本题共 4 个小题，每个小题 5 分，共 20 分） 13.若关于 x 的方程 有 4 个互不相等的实数根,则实数 m 的取值范围是______. 14.平面内有三点 ，且 ，则 x 为______． θ sin cos 2θ θ+ = 1tan tan θ θ+ ( ) 4 5f x x= 1 20 x x< < ( ) ( )1 21 2 ,2 2 f x f xx xf ++     ( ) ( )1 21 2 2 2 f x f xx xf ++  >   ( ) ( )1 21 2 2 2 f x f xx xf ++  <   ( ) ( )1 21 2 2 2 f x f xx xf ++  =   ( )f x [0, )+∞ (2 1) (1)f x f− < x ( 1,0)− (0,1) (1,2) ( 1,1)− 2 4 5x x m− + = (0, 3), (3,3), ( , 1)A B C x− − / /AB AC  15.将函数 的图象上所有的点向右平行移动 个单位长度,再把所得各点的横坐标 伸长到原来的 倍(纵坐标不变),所得图象的函数解析式是______________. 16.已知 ，则函数 的值域为______. 三、解答题（本题共 6 个题，共 70 分） 17.（本题满分 12 分） 已知向量 ， ， ． (1)求 ； (2)求满足 的实数 m，n；(3)若 ，求实数 k. 18.（本题满分 12 分） 已知三个点 . 1.求证: ; 2.要使四边形 为矩形,求点 的坐标,并求矩形 两对角线所夹锐角的余值。 19.（本题满分 12 分） 函数 的部分图象如图所示 1. 写出 的最小正周期及图中 的值; 2.求 在区间 上的最大值和最小值. 20.（本题满分 12 分） 设 为奇函数, 为常数. 1.求 的值; 2.判断函数 在区间 上的单调性并证明. 21.（本题满分 12 分） siny x= 10 π 2 51 22 x x −  ≤   2 4 1y x x= − + ( )3,2a= ),3( 1b= － ( )5,2c= 6 2a b c  ＋ － a mb nc  ＝ ＋ //( ) (2 )a kc b a   ＋ － ( ) ( ) ( )2,1 , 3,2 , 1,4A B D − AB AD⊥  ABCD C ABCD ( ) 3 (2 )6f x sin x π= + f ( )x 0 0,x y f ( )x [ , ]2 12 π π− − ( ) 1 2 1log 1 axf x x −= − a a ( )f x ( )1,+∞ 已知函数 . (1)化简 ; (2)若 ,且 ,求 的值; (3)若 ,求 的值. 22.（本题满分 10 分）已知定义在区间(0，＋∞)上的函数 f(x)满足 f(x1 x2 )＝f(x1)－f(x2)，且当 x>1 时，f(x)<0． ①求 f(1)的值； ②证明：f(x)为单调递减函数； ③若 f(3)＝－1，求 f(x)在[2，9]上的最小值． 3sin cos tan(2 )2 2( ) tan( )sin( )f α α α α α α π π   − + π −      = + π + π ( )f α 1( ) 2 8f fα α π ⋅ + = −   5 3 4 2 απ π≤ ≤ ( ) 2f fα α π + +   2 ( )2f fα απ + =   ( ) 2f fα α π ⋅ +   （理科试卷参考答案） 一、选择题 1.答案：D 解析： 2.答案：B 解析：由已知得函数 的定义域为 , 则 , , 所以函数的值域为 . 故正确答案为 B 3.答案：A 解析：∵ ,故选 A. 4.答案：C 解析：因为 ，所以 ，于是有 ，故本题选 C. 5.答案：A 解析：向左平移 个单位长度后得到 的图像,则其对称中心为 ;或将选项进行逐个验证. 6.答案：D 解析：本题主要考查平面向量基本定理及坐标表示. 因为 ， 所以 ， 所以 ， 解得 . 7.答案：B ta n 3α = 2c o s 0α ≠ 2 2 2 2 2 22 2 2 2 sin 2cos sin 2cos 2 11 sin cos sinsin cos sin tan tan 1 tancos cos 2 α α α α α α α α αα α α α α α + + += = =++ + ( ) 2 2f x x x= + { }2, 1,0,1− − ( ) ( ) ( )2 0, 1 1, 0 0f f f− = − = − = ( )1 3f = { }1,0,3− (1,2) (3,4) (4,6)AC AB BC= + = + =   π 6 1 πcos 22 3y x = +   π π ,0 ( )12 2 k k Z + ∈   a b⊥  0a b⋅ =  1 ( 2) ( 2) 0m m× + − × − = 4m = 解析：依题意得,最后得到的曲线相应的解析式是 ,故选 B 8.答案：D 解析：由 ，得 或 因此，函数 的定义域是 .注意到函数 在 上单调递增，由复合函数的单调性知， 的单调递增区间是 ，选 D. 9.答案：D 解析：令 ， 因为 ，所以 为奇函数，排除选项 A,B;因为 时， ，所以排除选项 C，选 D. 10.答案：D 解析：∵ ,∴ , 即 , 那么 . 11.答案：A 解析：幂函数 在 上是增函数,大致图像如图所示, 设 ,其中 ,则 的中点 E 的坐标为 ∵ ∴ 故选 A 12.答案：B 解析： 1 π π 1 πsin sin2 3 3 2 6y x x     = + − = −         2 2 8 0x x− − > 2x < − 4x > ( ) ( )2ln 2 8f x x x= − − ( ), 2 4,( ) ∪−∞ − +∞ 2 2 8y x x= − − (4, )+∞ ( ) ( )2ln 2 8f x x x= − − (4, )+∞ ( ) 2 sin 2xf x x= , ( ) 2 sin 2( ) 2 sin 2 ( )x xx R f x x x f x−∈ − = − = − = − ( ) 2 sin 2xf x x= π( ,π)2x∈ ( ) 0f x < sin cos 2θ θ+ = 1 2sin cos 2θ θ+ = 1sin cos 2 θ θ = 1 sin cos 1tan 2tan cos sin sin cos θ θθ θ θ θ θ θ+ = + = = ( ) 4 5f x x= ( )0,+∞ ( ) ( )1 2,0 , ,0A x C x 1 20 x x< < AC ( ) ( )1 2 1 2 1 2,0 , , ,2 2 x x x xAB f x CD f x EF f + +   = = =       ( )1 2EF AB CD> + ( ) ( )1 21 2 2 2 f x f xx xf ++  >   根据题意,由函数的奇偶性分析可得 f(2x-1) − −  1 21 x x< < 2 1 0x x− > 1 2 2 21 1 11 1x x    + > + >   − −    1 1 1 22 2 2 2log 1 log 11 1x x    + < +   − −    ( ) ( )2 1 0f x f x− > ( )f x ( )1,+∞ ( cos )sin ( tan )( ) costan ( sin )f α α αα αα α − −= = −− cos sin2 2f α α απ π   + = − + =       1( ) 2 8f fα α π ⋅ + = −   1cos sin 8 α α⋅ = 2 3(sin cos ) 4 α α− = 5 3 4 2 απ π≤ ≤ cos sinα α> 3( ) sin cos2 2f fα α α απ + + = − = −   (3) , 即 ,联立 ,解得 , 所以 . 解析： 22. 答案：(1) f(1)=0 (2) 略 (3) f(x)min=-2 2 ( )2f fα απ + =   sin 2cosα α= − 2 2sin cos 1α α+ = 2 1cos 5 α = 2 2( ) sin cos 2cos2 5f fα α α α απ ⋅ + = − = =  