高中数学第五章一元函数的导数及其应用5-1导数的概念及其意义5-1-1变化率问题课件新人教A版选择性必修第二册 28页

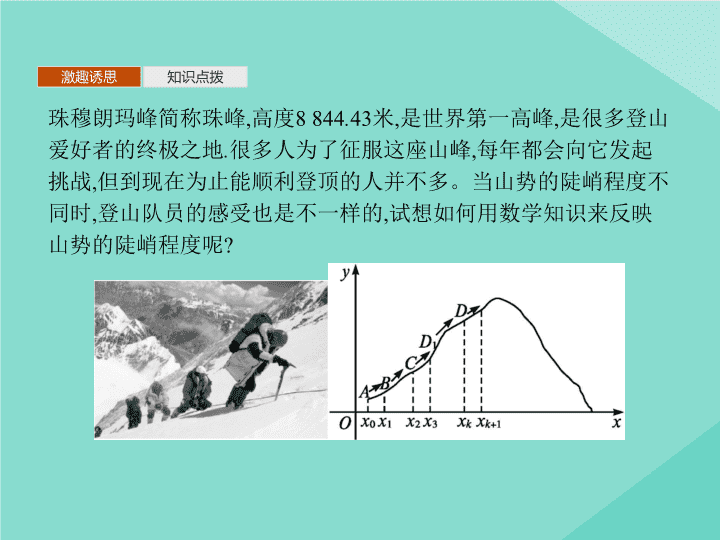
5.1.1 　变化率问题 激趣诱思 知识点拨 珠穆朗玛峰简称珠峰 , 高度 8 844 . 43 米 , 是世界第一高峰 , 是很多登山爱好者的终极之地 . 很多人为了征服这座山峰 , 每年都会向它发起挑战 , 但到现在为止能顺利登顶的人并不多。当山势的陡峭程度不同时 , 登山队员的感受也是不一样的 , 试想如何用数学知识来反映山势的陡峭程度呢 ? 激趣诱思 知识点拨 一、平均速度与瞬时速度 1 . 平均速度 : 物体的位移与所用时间的比值 , 通常指物体在 某一时间段 的速度 . 若物体运动的位移与时间的关系式是 s=f ( t ), 函数 f ( t ) 在 t 0 与 t 0 + Δ t 之间的平均速度是 2 . 瞬时速度 : 在物理中 , 做变速运动的物体在不同的时刻 , 速度是不同的 , 我们把物体在某一时刻的速度称为瞬时速度 . 激趣诱思 知识点拨 名师点析 从物理的角度看 , 瞬时速度就是将平均速度的时间段改为时间点 , 即让时间段 [ t , t+ Δ t ] 或者 [ t+ Δ t , t ] 中的时间间隔 | Δ t| 无限趋近于 0, 此时时间段 [ t , t+ Δ t ] 或者 [ t+ Δ t , t ] 内的平均速度就无限趋近于 t 时刻的瞬时速度 . 激趣诱思 知识点拨 微练习 一物体按规律 s ( t ) = 2 t 2 运动 , 则其在时间段 [1,2] 内的平均速度为 　　　　 , 在 t= 3 时的瞬时速度是 　　　　 .   答案 : 6 　 12 激趣诱思 知识点拨 微思考 平均速度与瞬时速度有什么不同 ? 提示 : 平均速度表示的是运动的物体在某或某一段时间内的快慢程度 . 瞬时速度反映的是物体在运动过程的某一时刻的运动情况 , 能精确表示任一时刻物体运动的快慢和方向 . 激趣诱思 知识点拨 二、割线斜率与切线斜率 1 . 割线与切线的关系 如图所示 , 当点 P n ( x n , f ( x n )) 沿着曲线无限接近点 P ( x 0 , f ( x 0 )) 时 , 割线 PP n 趋近于确定的位置。这个确定位置的直线 PT 称为曲线在点 P 处的切线。 激趣诱思 知识点拨 2 . 割线斜率与切线斜率的 关系 激趣诱思 知识点拨 微 练习 过曲线 y=f ( x ) = 图象 上一点 (2, - 2) 及邻近一点 (2 + Δ x , - 2 + Δ y ) 作割线 , 则当 Δ x= 0 . 5 时割线的斜率为 　　　　 , 在点 (2, - 2) 处的切线斜率为 　　　　 .   激趣诱思 知识点拨 微点拨 (1) 当 Δ x →0 时 , 割线 PP n 的斜率称为曲线在点 P 处的切线的斜率 . 这样就提供了求曲线上某点切线的斜率的一种方法 . (2) 曲线在某点处的切线 : ① 与该点的位置有关 . ② 要根据割线是否有极限位置来判断与求解 . 如割线有极限位置 , 则在此点有切线 , 且切线是唯一的 ; 如割线不存在极限位置 , 则曲线在此点处无切线 . ③ 曲线的切线 , 并不一定与曲线只有一个交点 , 可以有多个交点 . 探究一 探究二 素养形成 当堂检测 求物体运动的平均速度及瞬时速度 例 1 (2019 大同煤矿第四中学高二月考 ) 某质点沿曲线运动的方程为 f ( x ) =- 2 x 2 + 1( x 表示时间 , f ( x ) 表示位移 ), 则该质点从 x= 1 到 x= 2 的平均速度为 ( 　　 ) A .- 4 B .- 8 C . 6 D .- 6 解析 : 由题得该质点从 x= 1 到 x= 2 的平均速度 为 故选 D . 答案 : D 探究一 探究二 素养形成 当堂检测 反思感悟 求物体运动的平均速度的三个步骤 第一步 , 求时间的增量 Δ x=x 2 -x 1 ; 第二步 , 求位移的增量 Δ y=f ( x 2 ) -f ( x 1 ); 探究一 探究二 素养形成 当堂检测 变式训练 1 (2020 定远县育才学校高二月考 ) 质点的运动规律为 s=t 2 + 3( t 表示时间 , s 表示位移 ), 则在时间 [3,3 + Δ t ] 中 , 质点的平均速度等于 ( 　　 ) 答案 : A 探究一 探究二 素养形成 当堂检测 例 2 某物体的运动路程 s ( 单位 :m) 与时间 t ( 单位 :s) 的关系可用函数 s ( t ) =t 2 +t+ 1 表示 , 求物体在 t= 1 s 时的瞬时速度 . 分析 : 计算物体在 [1,1 + Δ t ](Δ t> 0) 或 [1 + Δ t ,1](Δ t< 0) 内的 平均速度 探究一 探究二 素养形成 当堂检测 延伸探究 1 在本例条件不变的前提下 , 试求物体的初速度 . 探究一 探究二 素养形成 当堂检测 延伸探究 2 在本例条件不变的前提下 , 试问物体在哪一时刻的瞬时速度为 9 m/s. 则 2 t 0 + 1 = 9, ∴ t 0 = 4 . 则物体在 4 s 时的瞬时速度为 9 m/s. 反思感悟 求运动物体在 t=t 0 的瞬时速度的三个步骤 (1) 求时间改变量 Δ t 和位移改变量 Δ s=s ( t 0 + Δ t ) -s ( t 0 ) . 探究一 探究二 素养形成 当堂检测 求解曲线在某点处的割线、切线斜率 例 3 设函数 f ( x ) =x ( x- 6), 则此函数图象在 x= 0 处的切线斜率为 ( 　　 ) A.0 B.-1 C.3 D.-6 答案 : D 探究一 探究二 素养形成 当堂检测 反思感悟 求曲线上某点处的割线或切线的 步骤 探究一 探究二 素养形成 当堂检测 A.-1 B.0 C.1 D.2 答案 : A 探究一 探究二 素养形成 当堂检测 求解较为复杂函数图象在某点处的斜率 问题 分析 : 利用立方和公式化简求解 . 答案 : B 探究一 探究二 素养形成 当堂检测 反思感悟 复杂函数在某点处的斜率求解 1 . 关键是利用公式进行合理准确的运算 . 2 . 常见的公式有 : (1) 平方差公式 : ( a+b )( a-b ) =a 2 -b 2 ; (2) 完全平方和与完全平方差公式 : ( a ± b ) 2 =a 2 ± 2 ab+b 2 ; (3) 立方差公式 : a 3 -b 3 = ( a-b )( a 2 +ab+b 2 ); 立方和公式 : a 3 +b 3 = ( a+b )( a 2 -ab+b 2 ) . (4) 完全立方差公式 : ( a-b ) 3 =a 3 - 3 a 2 b+ 3 ab 2 -b 3 . 完全立方和公式 : ( a+b ) 3 =a 3 + 3 a 2 b+ 3 ab 2 +b 3 . 探究一 探究二 素养形成 当堂检测 变式训练 已知曲线 y=x 4 +ax 2 + 1 在点 ( - 1, a+ 2) 处切线的斜率为 8, 则 a 的值是 ( 　　 ) A.9 B.6 C.-9 D.-6 =- 4 - 2 a= 8 . 故 a=- 6 . 答案 : D 探究一 探究二 素养形成 当堂检测 1 . (2020 河北石家庄二中高二月考 ) 函数 f ( x ) =x 2 在区间 [ - 1,2] 上的平均变化率为 ( 　　 ) A. - 1 B.1 C.2 D.3 解析 : 因为 f ( x ) =x 2 , 所以 f ( x ) 在区间 [ - 1,2] 上的平均变化率为 答案 : B 探究一 探究二 素养形成 当堂检测 2 . 已知一直线运动的物体 , 当时间从 t 变到 t+ Δ t 时 , 物体的位移 为 A . 时间从 t 变到 t+ Δ t 时物体的速度 B . 在 t 时刻该物体的瞬时速度 C . 当时间为 Δ t 时物体的速度 D . 时间从 t 变到 t+ Δ t 时物体的平均速度 答案 : B 探究一 探究二 素养形成 当堂检测 3 . (2020 陕西高二期末 ) 某运动物体的位移 s ( 单位 : 米 ) 关于时间 t ( 单位 : 秒 ) 的函数关系式为 s= 2 t+ 1, 则该物体在 t= 1 秒时的瞬时速度为 ( 　　 ) A . 1 米 / 秒 B . 2 米 / 秒 C . 3 米 / 秒 D . 4 米 / 秒 则物体在 t= 1 秒时的瞬时速度为 2 米 / 秒 . 故选 B . 答案 : B 探究一 探究二 素养形成 当堂检测 4 . (2019 全国高一课时练习 ) 过曲线 y=x 2 上两点 A (2,4) 和 B (2 + Δ x ,4 + Δ y ) 作割线 , 当 Δ x= 0 . 1 时 , 割线 AB 的斜率为 　　　　　 .   答案 : 4 . 1 探究一 探究二 素养形成 当堂检测 5 . 函数 f ( x ) =x 2 - 2 x+ 1 在 x= 4 处切线的斜率为 　　　 .   答案 : 6