2020_2021学年新教材高中数学第7章三角函数章末综合提升教学案含解析苏教版必修第一册 9页

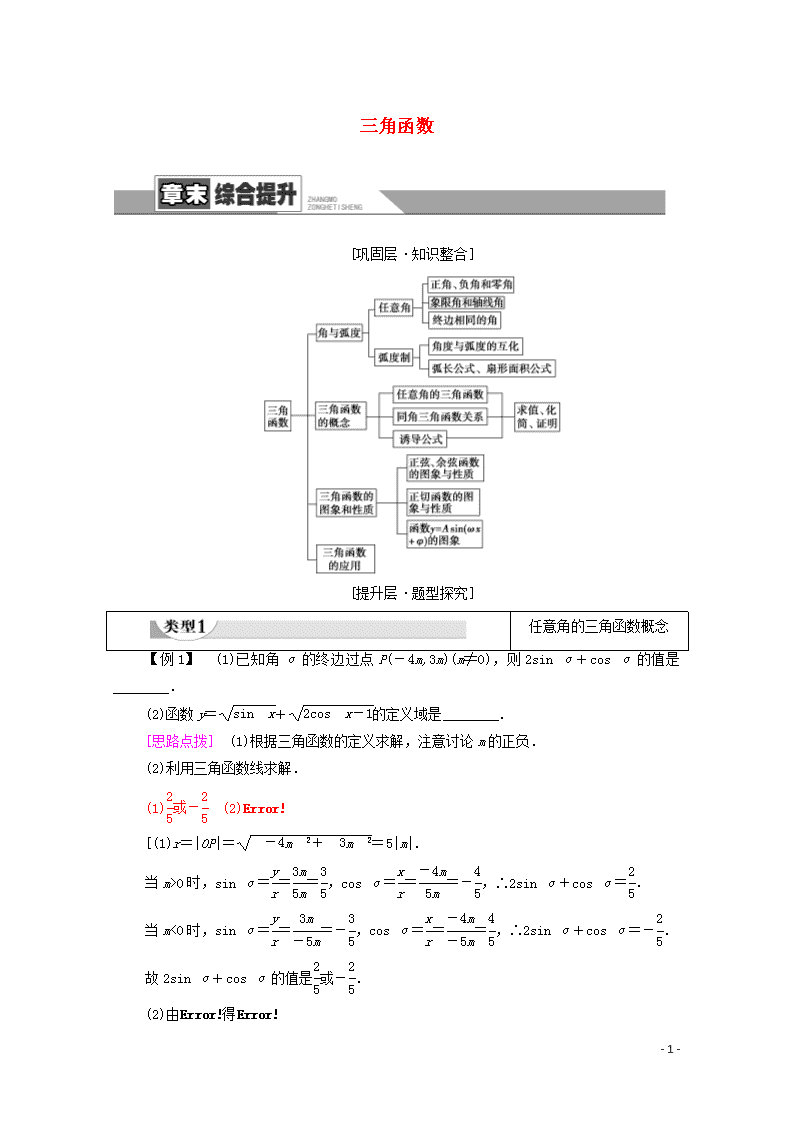
三角函数 ‎[巩固层·知识整合]‎ ‎[提升层·题型探究]‎ 任意角的三角函数概念 ‎【例1】　(1)已知角α的终边过点P(－‎4m,‎3m)(m≠0)，则2sin α＋cos α的值是________．‎ ‎(2)函数y＝＋的定义域是________．‎ ‎[思路点拨]　(1)根据三角函数的定义求解，注意讨论m的正负．‎ ‎(2)利用三角函数线求解．‎ ‎(1)或－　(2) ‎[(1)r＝|OP|＝＝5|m|．‎ 当m>0时，sin α＝＝＝，cos α＝＝＝－，∴2sin α＋cos α＝．‎ 当m<0时，sin α＝＝＝－，cos α＝＝＝，∴2sin α＋cos α＝－．‎ 故2sin α＋cos α的值是或－．‎ ‎(2)由得 - 9 -‎ 如图，结合三角函数线知：‎ 解得2kπ≤x≤2kπ＋(k∈Z)，‎ ‎∴函数的定义域为 ．]‎ 三角函数的概念所涉及的内容主要有以下两方面：‎ (1)任意角和弧度制.理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算.‎ (2)任意角的三角函数.掌握任意角的正弦、余弦、正切的定义及三角函数线，能够利用三角函数线判断三角函数的符号，借助三角函数线求三角函数的定义域.‎ ‎1．(1)已知角α的顶点在原点，始边为x轴的非负半轴．若角α的终边经过点P(－，y)，且sin α＝y(y≠0)，判断角α所在的象限，并求cos α和tan α的值；‎ ‎(2)若角α的终边在直线y＝－3x上，求10sin α＋的值．‎ ‎[解]　(1)依题意，点P到原点O的距离为|PO|＝，∴sin α＝＝＝y．‎ ‎∵y≠0，∴9＋3y2＝16，∴y2＝，‎ ‎∴y＝±．‎ ‎∴点P在第二或第三象限．‎ 当点P在第二象限时，y＝，cos α＝＝－，tan α＝－．‎ 当点P在第三象限时，y＝－，cos α＝＝－，‎ - 9 -‎ tan α＝．‎ ‎(2)设角α终边上任一点为P(k，－3k)(k≠0)，‎ 则r＝＝＝|k|．‎ 当k>0时，r＝k．‎ ‎∴sin α＝＝－，＝＝．‎ ‎∴10sin α＋＝－3＋3＝0．‎ 当k<0时，r＝－k．‎ ‎∴sin α＝＝，＝＝－．‎ ‎∴10sin α＋＝3－3＝0．‎ 综上，10sin α＋＝0．‎ 同角三角函数的基本关系与诱导公式 ‎【例2】　已知关于x的方程2x2－(＋1)x＋m＝0的两根为sin θ，cos θ，θ∈(0,2π)．求：‎ ‎(1)＋；‎ ‎(2)m的值；‎ ‎(3)方程的两根及此时θ的值．‎ ‎[思路点拨]　先利用根与系数的关系得到sin θ＋cos θ与sin θcos θ，再利用诱导公式和三角函数的基本关系式求解．‎ ‎[解]　由根与系数的关系，得 sin θ＋cos θ＝，sin θcos θ＝．‎ ‎(1)原式＝＋＝＋＝－＝sin θ＋cos θ＝．‎ ‎(2)由sin θ＋cos θ＝，两边平方可得1＋2sin θcos θ＝，把sin θcos θ＝‎ - 9 -‎ 代入得1＋2×＝1＋，∴m＝．‎ ‎(3)由m＝可解方程2x2－(＋1)x＋＝0，‎ 得两根为和．∴或 ‎∵θ∈(0,2π)，‎ ‎∴θ＝或．‎ 同角三角函数的基本关系和诱导公式是三角恒等变换的主要依据，主要应用方向是三角函数式的化简、求值和证明.常用以下方法技巧：(1)化弦：当三角函数式中三角函数名称较多时，往往把三角函数化为弦，再化简变形.(2)化切：当三角函数式中含有正切及其他三角函数时，有时可将三角函数名称都化为正切，再化简变形.(3)“1”的代换：在三角函数式中，有些会含有常数1，常数1虽然非常简单，但有些三角函数式的化简却需要利用三角函数公式将1代换为三角函数式.‎ ‎2．已知f(α)＝．‎ ‎(1)化简f(α)；‎ ‎(2)若f(α)＝，且<α<，求cos α－sin α的值；‎ ‎(3)若α＝－，求f(α)的值．‎ ‎[解]　(1)f(α)＝＝sin α·cos α．‎ ‎(2)由f(α)＝sin α·cos α＝可知，(cos α－sin α)2＝cos2α－2sin α·cos α＋sin2α ‎＝1－2sin α·cos α＝1－2×＝．‎ 又∵<α<，∴cos α|cos x|成立的x的取值范围是(　　)‎ A． B．∪ C． D． A　[sin x>|cos x|，∴sin x>0，∴x∈(0，π)．在同一坐标系中画出y＝sin x，x∈(0，π)与y＝|cos x|，x∈(0，π)的图象，如图．‎ - 9 -‎ 观察图象易得使sin x>|cos x|成立的x∈，故选A．]‎ - 9 -‎