2018年河南省开封市高考数学一模试卷（文科） 23页

‎2018年河南省开封市高考数学一模试卷（文科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）设集合A={1，3，5，7}，B={x|2≤x≤5}，则A∩B的真子集个数为（　　）‎ A．2个 B．3个 C．4个 D．8个 ‎2．（5分）复数在复平面内对应的点在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3．（5分）已知向量=（m﹣1，1），=（m，﹣2），则“m=2”是“⊥”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．（5分）在△ABC中，a=2，b=，B=，则A=（　　）‎ A． B． C． D．或 ‎5．（5分）若，则sin2α=（　　）‎ A． B． C． D．‎ ‎6．（5分）如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损，则乙的平均成绩超过甲的平均成绩的概率为（　　）‎ A． B． C． D．‎ ‎7．（5分）已知曲线﹣=1（a＞0，b＞0）为等轴双曲线，且焦点到渐近线的距离为，则该双曲线的方程为（　　）‎ A． B．x2﹣y2=1 C． D．x2﹣y2=2‎ ‎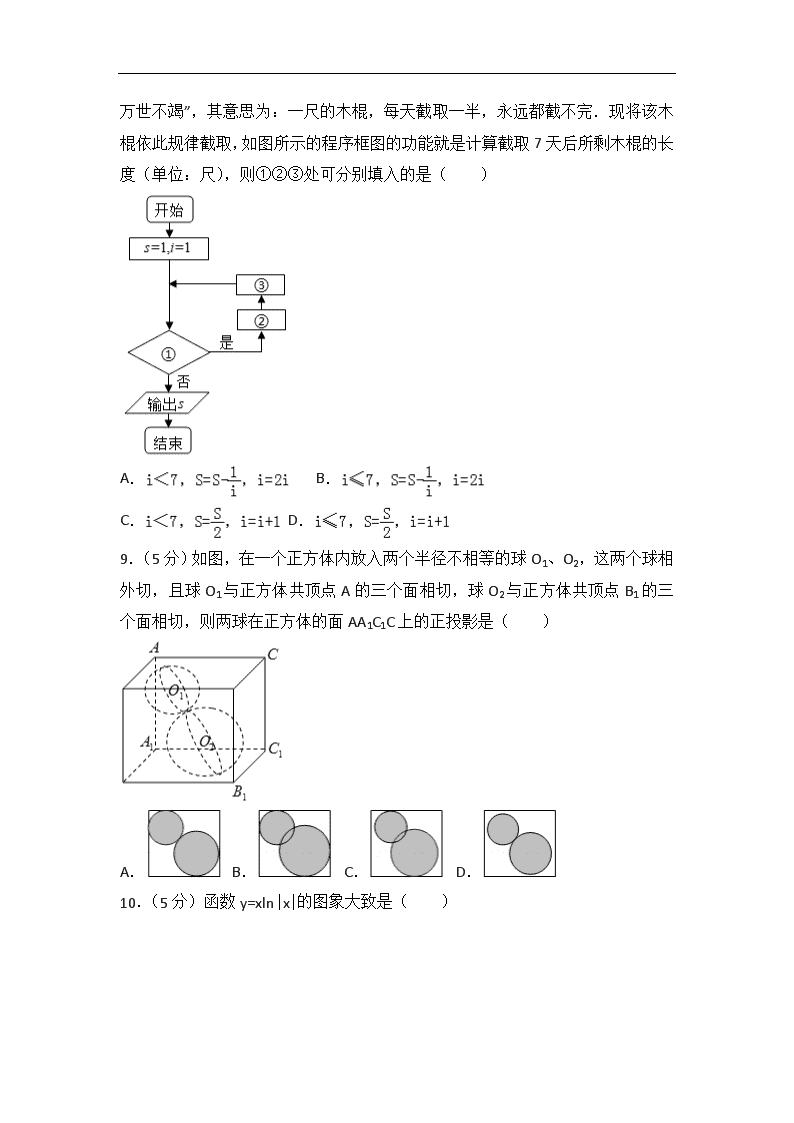8．（5分）我国古代名著《庄子•天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完．现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（　　）‎ A． B．‎ C． D．‎ ‎9．（5分）如图，在一个正方体内放入两个半径不相等的球O1、O2，这两个球相外切，且球O1与正方体共顶点A的三个面相切，球O2与正方体共顶点B1的三个面相切，则两球在正方体的面AA1C1C上的正投影是（　　）‎ A． B． C． D．‎ ‎10．（5分）函数y=xln|x|的图象大致是（　　）‎ A． B． C． D．‎ ‎11．（5分）抛物线M：y2=4x的准线与x轴交于点A，点F为焦点，若抛物线M上一点P满足PA⊥PF，则以F为圆心且过点P的圆被y轴所截得的弦长约为（参考数据：≈2.24）（　　）‎ A． B． C． D．‎ ‎12．（5分）已知函数，若函数F（x）=f（x）﹣3的所有零点依次记为x1，x2，x3，…，xn，且x1＜x2＜x3＜…＜xn，则x1+2x2+2x3+…+2xn﹣1+xn=（　　）‎ A． B．445π C．455π D．‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．（5分）则f（f（2））的值为　 　．‎ ‎14．（5分）已知函数f（x）=ax3+bx+1的图象在点（1，f（1））处的切线方程为4x﹣y﹣1=0，则a+b=　 　．‎ ‎15．（5分）设x，y满足约束条件，且x，y∈Z，则z=3x+5y的最大值为　 　．‎ ‎16．（5分）一个棱长为5的正四面体（棱长都相等的三棱锥）纸盒内放一个小正四面体，若小正四面体在纸盒内可以任意转动，则小正四面体的棱长的最大值为　 　．‎ ‎　‎ 三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（12分）已知正项等比数列{an}满足a3a9=4a52，a2=1．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）记bn=2nan，求数列{bn}的前n项和Sn．‎ ‎18．（12分）如图1，在矩形ABCD中，AD=2AB=4，E是AD的中点．将△ABE沿BE折起使A到点P的位置，平面PEB⊥平面BCDE，如图2．‎ ‎（Ⅰ）求证：PB⊥平面PEC；‎ ‎（Ⅱ）求三棱锥D﹣PEC的高．‎ ‎19．（12分）近年来我国电子商务行业迎来蓬勃发展的新机遇，2017年双11期间，某购物平台的销售业绩高达1271亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．‎ ‎（Ⅰ）完成下面的 2×2列联表，并回答是否有99%的把握，认为商品好评与服务好评有关？‎ 对服务好评 对服务不满意 合计 对商品好评 对商品不满意 合计 ‎200‎ ‎（Ⅱ）若针对商品的好评率，采用分层抽样的方式从这200次交易中取出5次交易，并从中选择两次交易进行客户回访，求至少有一次好评的概率．‎ 附：‎ P（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎（，其中n=a+b+c+d）‎ ‎20．（12分）给定椭圆C：+=1（a＞b＞0），称圆心在原点O，半径为的圆是椭圆C的“准圆”．已知椭圆C的离心率，其“准圆”的方程为x2+y2=4．‎ ‎（I）求椭圆C的方程；‎ ‎（II）点P是椭圆C的“准圆”上的动点，过点P作椭圆的切线l1，l2交“准圆”于点M，N．‎ ‎（1）当点P为“准圆”与y轴正半轴的交点时，求直线l1，l2的方程，并证明l1⊥l2；‎ ‎（2）求证：线段MN的长为定值．‎ ‎21．（12分）已知函数f（x）=（t﹣1）xex，g（x）=tx+1﹣ex．‎ ‎（Ⅰ）当t≠1时，讨论f（x）的单调性；‎ ‎（Ⅱ）f（x）≤g（x）在[0，+∞）上恒成立，求t的取值范围．‎ ‎　‎ 选修4-4：极坐标与参数方程 ‎22．（10分）已知直线l：3x﹣y﹣6=0，在以坐标原点O为极点，x轴正半轴为极轴的极坐标系中，曲线C：ρ﹣4sinθ=0．‎ ‎（Ⅰ）将直线l写成参数方程（t为参数，α∈[0，π），）的形式，并求曲线C的直角坐标方程；‎ ‎（Ⅱ）过曲线C上任意一点P作倾斜角为30°的直线，交l于点A，求|AP|的最值．‎ ‎　‎ 选修4-5：不等式选讲 ‎23．已知关于x的不等式|x+1|+|2x﹣1|≤3的解集为{x|m≤x≤n}．‎ ‎（I）求实数m、n的值；‎ ‎（II）设a、b、c均为正数，且a+b+c=n﹣m，求++的最小值．‎ ‎　‎ ‎2018年河南省开封市高考数学一模试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）设集合A={1，3，5，7}，B={x|2≤x≤5}，则A∩B的真子集个数为（　　）‎ A．2个 B．3个 C．4个 D．8个 ‎【解答】解：集合A={1，3，5，7}，B={x|2≤x≤5}，‎ 则A∩B={3，5}，‎ ‎∴A∩B的真子集是∅，{3}，{5}，共3个．‎ 故选：B．‎ ‎　‎ ‎2．（5分）复数在复平面内对应的点在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【解答】解：∵=，‎ ‎∴复数在复平面内对应的点的坐标为（），在第四象限．‎ 故选：D．‎ ‎　‎ ‎3．（5分）已知向量=（m﹣1，1），=（m，﹣2），则“m=2”是“⊥”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【解答】解：∵=（m﹣1，1），=（m，﹣2），‎ ‎∴⇔m（m﹣1）﹣2=0．‎ 由m（m﹣1）﹣2=0，解得m=﹣1或m=2．‎ ‎∴“m=2”是“⊥”的充分不必要条件．‎ 故选：A．‎ ‎　‎ ‎4．（5分）在△ABC中，a=2，b=，B=，则A=（　　）‎ A． B． C． D．或 ‎【解答】解：在△ABC中，∵a=2，b=，B=，‎ ‎∴由正弦定理可得：sinA===，‎ ‎∵A∈（，π），‎ ‎∴A=或．‎ 故选：D．‎ ‎　‎ ‎5．（5分）若，则sin2α=（　　）‎ A． B． C． D．‎ ‎【解答】解：∵，‎ ‎∴sin2α=﹣cos（）=﹣cos2（）‎ ‎=﹣[2﹣1]=1﹣=1﹣2×=．‎ 故选：C．‎ ‎　‎ ‎6．（5分）如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损，则乙的平均成绩超过甲的平均成绩的概率为（　　）‎ A． B． C． D．‎ ‎【解答】解：茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损，‎ 甲的平均成绩为：=（88+89+90+91+92）=90，‎ ‎∵乙的平均成绩超过甲的平均成绩，‎ 设数字被污损为x，‎ ‎∴83+83+87+（90+x）+99＞450，x＞8，‎ ‎∴x=9，‎ ‎∴乙的平均成绩超过甲的平均成绩的概率为p=．‎ 故选：A．‎ ‎　‎ ‎7．（5分）已知曲线﹣=1（a＞0，b＞0）为等轴双曲线，且焦点到渐近线的距离为，则该双曲线的方程为（　　）‎ A． B．x2﹣y2=1 C． D．x2﹣y2=2‎ ‎【解答】解：根据题意，若曲线﹣=1（a＞0，b＞0）为等轴双曲线，则a2=b2，‎ c==a，即焦点的坐标为（±a，0）；‎ 其渐近线方程为x±y=0，‎ 若焦点到渐近线的距离为，则有=a=，‎ 则双曲线的标准方程为﹣=1，即x2﹣y2=2；‎ 故选：D．‎ ‎　‎ ‎8．（5分）我国古代名著《庄子•天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完．现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（　　）‎ A． B．‎ C． D．‎ ‎【解答】解：由题意可得：由图可知第一次剩下，第二次剩下，…由此得出第7次剩下，‎ 可得①为i≤7？‎ ‎②s=‎ ‎③i=i+1‎ 故选：D．‎ ‎　‎ ‎9．（5分）如图，在一个正方体内放入两个半径不相等的球O1、O2，这两个球相外切，且球O1与正方体共顶点A的三个面相切，球O2与正方体共顶点B1的三个面相切，则两球在正方体的面AA1C1C上的正投影是（　　）‎ A． B． C． D．‎ ‎【解答】解：由题意可以判断出两球在正方体的面AA1C1C上的正投影与正方形相切，排除C、D，把其中一个球扩大为与正方体相切，则另一个球被挡住一部分，由于两球不等，所以排除A；B正确；‎ 故选B ‎　‎ ‎10．（5分）函数y=xln|x|的图象大致是（　　）‎ A． B． C． D．‎ ‎【解答】解：∵函数f（x）=xln|x|，可得f（﹣x）=﹣f（x），‎ f（x）是奇函数，其图象关于原点对称，排除A，D，‎ 当x→0时，f（x）→0，故排除B 又f′（x）=lnx+1，令f′（x）＞0得：x＞，得出函数f（x）在（，+∞）上是增函数，‎ 故选：C．‎ ‎　‎ ‎11．（5分）抛物线M：y2=4x的准线与x轴交于点A，点F为焦点，若抛物线M上一点P满足PA⊥PF，则以F为圆心且过点P的圆被y轴所截得的弦长约为（参考数据：≈2.24）（　　）‎ A． B． C． D．‎ ‎【解答】解：由题意，A（﹣1，0），F（1，0），‎ 点P在以AF为直径的圆x2+y2=1上．‎ 设点P的横坐标为m，联立圆与抛物线的方程得x2+4x﹣1=0，‎ ‎∵m＞0，∴m=﹣2+，‎ ‎∴点P的横坐标为﹣2+，‎ ‎∴|PF|=m+1=﹣1+，‎ ‎∴圆F的方程为（x﹣1）2+y2=（﹣1）2，‎ 令x=0，可得y=±，‎ ‎∴|EF|=2=2=，‎ 故选：D．‎ ‎　‎ ‎12．（5分）已知函数，若函数F（x）=f（x）﹣3的所有零点依次记为x1，x2，x3，…，xn，且x1＜x2＜x3＜…＜xn，则x1+2x2+2x3+…+2xn﹣1+xn=（　　）‎ A． B．445π C．455π D．‎ ‎【解答】解：函数，‎ 令2x﹣=+kπ得x=+，k∈Z，即f（x）的对称轴方程为x=+，k∈Z．‎ ‎∵f（x）的最小正周期为T=π，0≤x≤，‎ 当k=30时，可得x=，‎ ‎∴f（x）在[0，]上有30条对称轴，‎ 根据正弦函数的性质可知：函数与y=3的交点x1，x2关于对称，x2，x3关于对称，…，‎ 即x1+x2=×2，x2+x3=×2，…，xn﹣1+xn=2×（）‎ 将以上各式相加得：x1+2x2+2x3+…+2x28+x29=2（++…+）=（2+5+8+…+89）×=455π 则x1+2x2+2x3+…+2xn﹣1+xn=（x1+x2）+（x2+x3）+x3+…+xn﹣1+（xn﹣1+xn）=2（）=455π，‎ 故选：C ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．（5分）则f（f（2））的值为　2　．‎ ‎【解答】解：由题意，自变量为2，‎ 故内层函数f（2）=log3（22﹣1）=1＜2，‎ 故有f（1）=2×e1﹣1=2，‎ 即f（f（2））=f（1）=2×e1﹣1=2，‎ 故答案为 2‎ ‎　‎ ‎14．（5分）已知函数f（x）=ax3+bx+1的图象在点（1，f（1））处的切线方程为4x﹣y﹣1=0，则a+b=　2　．‎ ‎【解答】解：函数f（x）=ax3+bx+1的导数为f′（x）=3ax2+b，‎ f（x）的图象在点（1，f（1））处的切线方程为4x﹣y﹣1=0，‎ 可得3a+b=4，f（1）=3=a+b+1，‎ 解得a=1，b=1，‎ 则a+b=2．‎ 故答案为：2．‎ ‎　‎ ‎15．（5分）设x，y满足约束条件，且x，y∈Z，则z=3x+5y的最大值为　13　．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 作出直线3x+5y=0，‎ ‎∵x，y∈Z，‎ ‎∴平移直线3x+5y=0至（1，2）时，目标函数z=3x+5y的最大值为13．‎ 故答案为：13．‎ ‎　‎ ‎16．（5分）一个棱长为5的正四面体（棱长都相等的三棱锥）纸盒内放一个小正四面体，若小正四面体在纸盒内可以任意转动，则小正四面体的棱长的最大值为　　．‎ ‎【解答】解：∵在此纸盒内放一个小正四面体，若小正四面体在纸盒内可以任意转动，‎ ‎∴小正四面体的外接球是纸盒的内切球，‎ 设正四面体的棱长为a，则内切球的半径为a，外接球的半径是a，‎ ‎∴纸盒的内切球半径是=，‎ 设小正四面体的棱长是x，则=x，解得x=，‎ ‎∴小正四面体的棱长的最大值为，‎ 故答案为：．‎ ‎　‎ 三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（12分）已知正项等比数列{an}满足a3a9=4a52，a2=1．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）记bn=2nan，求数列{bn}的前n项和Sn．‎ ‎【解答】解：（Ⅰ）正项等比数列{an}满足a3a9=4a52，a2=1．‎ 则：，‎ 解得：，‎ 所以：；‎ ‎（Ⅱ）由于：，‎ 则：=n•2n﹣1，‎ 所以：+…+n•2n﹣1①，‎ 则：+…+n•2n②‎ ‎①﹣②得：，‎ 即：．‎ ‎　‎ ‎18．（12分）如图1，在矩形ABCD中，AD=2AB=4，E是AD的中点．将△ABE沿BE折起使A到点P的位置，平面PEB⊥平面BCDE，如图2．‎ ‎（Ⅰ）求证：PB⊥平面PEC；‎ ‎（Ⅱ）求三棱锥D﹣PEC的高．‎ ‎【解答】解：（Ⅰ）证明：∵AD=2AB，E为线段AD的中点，‎ ‎∴AB=AE，‎ 取BE中点O，连接PO，则PO⊥BE，‎ 又平面PEB⊥平面BCDE，平面PEB∩平面BCDE=BE，‎ ‎∴PO⊥平面BCDE，则PO⊥EC，‎ 在矩形ABCD中，∴AD=2AB，E为AD的中点，‎ ‎∴BE⊥EC，则EC⊥平面PBE，‎ ‎∴EC⊥PB，‎ 又PB⊥PE，且PE∩EC=E，‎ ‎∴PB⊥平面PEC．‎ ‎（Ⅱ）以OB所在直线为x轴，以平行于EC所在直线为y轴，以OP所在直线为z轴建立空间直角坐标系，‎ ‎∵PB=PE=2，则B（，0，0），E（﹣，0，0），P（0，0，），D（﹣2，，0），C（﹣，2，0），‎ ‎∴=（﹣，0，﹣），=（﹣，2，﹣），‎ ‎∴cos∠EPC===，可得：sin∠EPC==，可得：S△EPC=||•||•sin∠EPC=2×2×=2，‎ ‎∵VP﹣ECD=VD﹣EPC，设三棱锥D﹣PEC的高为h，则可得：S△ECD•OP=S△EPC•h，可得：=2×h，‎ ‎∴解得：三棱锥D﹣PEC的高h=1．‎ ‎　‎ ‎19．（12分）近年来我国电子商务行业迎来蓬勃发展的新机遇，2017年双11期间，某购物平台的销售业绩高达1271亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．‎ ‎（Ⅰ）完成下面的 2×2列联表，并回答是否有99%的把握，认为商品好评与服务好评有关？‎ 对服务好评 对服务不满意 合计 对商品好评 对商品不满意 合计 ‎200‎ ‎（Ⅱ）若针对商品的好评率，采用分层抽样的方式从这200次交易中取出5次交易，并从中选择两次交易进行客户回访，求至少有一次好评的概率．‎ 附：‎ P（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎（，其中n=a+b+c+d）‎ ‎【解答】解：（Ⅰ）根据题意，对商品好评次数为200×0.6=120，‎ 对服务好评次数为200×0.75=150，‎ 填写2×2列联表如下； ‎ 对服务好评 对服务不满意 合计 对商品好评 ‎80‎ ‎40‎ ‎120‎ 对商品不满意 ‎70‎ ‎10‎ ‎80‎ 合计 ‎150‎ ‎50‎ ‎200‎ 计算K2=≈11.11＞6.635，‎ ‎∴有99%的把握认为商品好评与服务好评有关；‎ ‎（Ⅱ）根据分层抽样原理，从这200次交易中取出5次交易，‎ 抽取商品好评次数为120×=3，不满意次数为2，‎ 分别记为a、b、c、D、E，从中选择两次交易，基本事件为 ab、ac、aD、aE、bc、bD、bE、cD、cE、DE共10种，‎ 至少有一次好评的事件为 ab、ac、aD、aE、bc、bD、bE、cD、cE共9种，‎ 故所求的概率为P=．‎ ‎　‎ ‎20．（12分）给定椭圆C：+=1（a＞b＞0），称圆心在原点O，半径为的圆是椭圆C的“准圆”．已知椭圆C的离心率，其“准圆”的方程为x2+y2=4．‎ ‎（I）求椭圆C的方程；‎ ‎（II）点P是椭圆C的“准圆”上的动点，过点P作椭圆的切线l1，l2交“准圆”于点M，N．‎ ‎（1）当点P为“准圆”与y轴正半轴的交点时，求直线l1，l2的方程，并证明l1⊥l2；‎ ‎（2）求证：线段MN的长为定值．‎ ‎【解答】解：（I）由准圆方程为x2+y2=4，则a2+b2=4，椭圆的离心率e===，‎ 解得：a=，b=1，‎ ‎∴椭圆的标准方程：；‎ ‎（Ⅱ）证明：（1）∵准圆x2+y2=4与y轴正半轴的交点为P（0，2），‎ 设过点P（0，2）且与椭圆相切的直线为y=kx+2，‎ 联立，整理得（1+3k2）x2+12kx+9=0．‎ ‎∵直线y=kx+2与椭圆相切，∴△=144k2﹣4×9（1+3k2）=0，解得k=±1，‎ ‎∴l1，l2方程为y=x+2，y=﹣x+2．∵=1，=﹣1，‎ ‎∴•=﹣1，则l1⊥l2．‎ ‎（2）①当直线l1，l2中有一条斜率不存在时，不妨设直线l1斜率不存在，‎ 则l1：x=±，‎ 当l1：x=时，l1与准圆交于点（，1）（，﹣1），‎ 此时l2为y=1（或y=﹣1），显然直线l1，l2垂直；‎ 同理可证当l1：x=时，直线l1，l2垂直．‎ ‎②当l1，l2斜率存在时，设点P（x0，y0），其中x02+y02=4．‎ 设经过点P（x0，y0）与椭圆相切的直线为y=t（x﹣x0）+y0，‎ ‎∴由得 （1+3t2）x2+6t（y0﹣tx0）x+3（y0﹣tx0）2﹣3=0．‎ 由△=0化简整理得 （3﹣x02）t2+2x0y0t+1﹣y02=0，‎ ‎∵x02+y02=4．，∴有（3﹣x02）t2+2x0y0t+（x02﹣3）=0．‎ 设l1，l2的斜率分别为t1，t2，‎ ‎∵l1，l2与椭圆相切，∴t1，t2满足上述方程（3﹣x02）t2+2x0y0t+（x02﹣3）=0，‎ ‎∴t1•t2=﹣1，即l1，l2垂直．‎ 综合①②知：∵l1，l2经过点P（x0，y0），又分别交其准圆于点M，N，且l1，l2‎ 垂直．‎ ‎∴线段MN为准圆x2+y2=4的直径，|MN|=4，‎ ‎∴线段MN的长为定值．‎ ‎　‎ ‎21．（12分）已知函数f（x）=（t﹣1）xex，g（x）=tx+1﹣ex．‎ ‎（Ⅰ）当t≠1时，讨论f（x）的单调性；‎ ‎（Ⅱ）f（x）≤g（x）在[0，+∞）上恒成立，求t的取值范围．‎ ‎【解答】解：（Ⅰ）由f（x）=（t﹣1）xex，得f′（x）=（t﹣1）（x+1）ex，‎ 若t＞1，则x＜﹣1时，f′（x）＜0，f（x）递减，x＞﹣1时，f′（x）＞0，f（x）递增，‎ 若t＜1，则x＜﹣1时，f′（x）＞0，f（x）递增，x＞﹣1时，f′（x）＜0，f（x）递减，‎ 故t＞1时，f（x）在（﹣∞，﹣1）递减，在（﹣1，+∞）递增，‎ t＜1时，f（x）在（﹣∞，﹣1）递增，在（﹣1，+∞）递减；‎ ‎（2）f（x）≤g（x）在[0，+∞）上恒成立，‎ 即（t﹣1）xex﹣tx﹣1+ex≤0对∀x≥0成立，‎ 设h（x）=（t﹣1）xex﹣tx﹣1+ex，‎ h（0）=0，h′（x）=（t﹣1）（x+1）ex﹣t+ex，h′（0）=0，‎ h″（x）=ex[（t﹣1）x+2t﹣1]，‎ t=1时，h″（x）=ex≥0，h′（x）在[0，+∞）递增，‎ ‎∴h′（x）≥h′（0）=0，故h（x）在[0，+∞）递增，‎ 故h（x）≥h（0）=0，显然不成立，‎ ‎∴t≠1，则h″（x）=ex（x+）（t﹣1），‎ 令h″（x）=0，则x=﹣，‎ ‎①当﹣≤0即t＜或t＞1时，‎ 若t≤，则h″（x）在[0，+∞）为负，h′（x）递减，‎ 故有h′（x）≤h′（0）=0，h（x）在[0，+∞）递减，‎ ‎∴h（x）≤h（0）=0成立，‎ 若t≥1，则h″（x）在[0，+∞）上为正，h′（x）递增，‎ 故有h′（x）≥h′（0）=0，故h（x）在[0，+∞）递增，‎ 故h（x）≥h（0）=0，不成立，‎ ‎②﹣≥0即≤t≤1时，‎ h″（x）在[0，﹣）内有h′（x）≥h′（0）=0，h（x）递增，‎ 故h（x）在[0，﹣）内有h（x）≥h（0）=0不成立，‎ 综上，t的范围是（﹣∞，]．‎ ‎　‎ 选修4-4：极坐标与参数方程 ‎22．（10分）已知直线l：3x﹣y﹣6=0，在以坐标原点O为极点，x轴正半轴为极轴的极坐标系中，曲线C：ρ﹣4sinθ=0．‎ ‎（Ⅰ）将直线l写成参数方程（t为参数，α∈[0，π），）的形式，并求曲线C的直角坐标方程；‎ ‎（Ⅱ）过曲线C上任意一点P作倾斜角为30°的直线，交l于点A，求|AP|的最值．‎ ‎【解答】解：（Ⅰ）直线l：3x﹣y﹣6=0，转化为直角坐标方程为：（t为参数），‎ 曲线C：ρ﹣4sinθ=0．转化为直角坐标方程为：x2+y2﹣4y=0．‎ ‎（Ⅱ）首先把x2+y2﹣4y=0的方程转化为：x2+（y﹣2）2=4，‎ 所以经过圆心，且倾斜角为30°的直线方程为：，‎ 则：，‎ 解得：，‎ 则：=，‎ 则：|AP|的最大值为：，‎ ‎|AP|的最小值为：．‎ ‎　‎ 选修4-5：不等式选讲 ‎23．已知关于x的不等式|x+1|+|2x﹣1|≤3的解集为{x|m≤x≤n}．‎ ‎（I）求实数m、n的值；‎ ‎（II）设a、b、c均为正数，且a+b+c=n﹣m，求++的最小值．‎ ‎【解答】解：（Ⅰ）∵|x+1|+|2x﹣1|≤3，‎ ‎∴或或，‎ 解得：﹣1≤x≤1，‎ 故m=﹣1，n=1；‎ ‎（Ⅱ）由（Ⅰ）a+b+c=2，‎ 则++‎ ‎=（++）（a+b+c）‎ ‎=[1+1+1+（+）+（+）+（+）]‎ ‎≥+（2+2+2）‎ ‎=+3=，‎ 当且仅当a=b=c=时“=”成立．‎ ‎　‎