高中数学必修2教案：2_3_1直线与平面垂直的判定 (4) 5页

第一课时 直线与平面垂直的判定 ‎（一）教学目标 ‎1．知识与技能 ‎（1）使学生掌握直线和平面垂直的定义及判定定理；‎ ‎（2）使学生掌握直线和平面所成的角求法；‎ ‎（3）培养学生的几何直观能力，使他们在直观感知，操作确认的基础上学会归纳、概括结论.‎ ‎2．过程与方法 ‎（1）通过教学活动，使学生了解，感受直线和平面垂直的定义的形成过程；‎ ‎（2）探究判定直线与平面垂直的方法.‎ ‎3．情态、态度与价值观 培养学生学会从“感性认识”到“理性认识”过程中获取新知.‎ ‎（二）教学重点、难点 重点：（1）直线与平面垂直的定义和判定定理；‎ ‎ （2）直线和平面所成的角.‎ 难点：直线与平面垂直判定定理的探究.‎ 教学过程 教学内容 师生互动 设计意图 新课导入 问题：直线和平面平行的判定方法有几种？‎ 师投影问题，学生回答.‎ 生：可用定义可判断，也可依判定定理判断.‎ 复习巩固 探索新知 一、直线和平面垂直的定义、画法 如果直线l与平面内的任意一条直线都垂直，我们说直线l与平面互相垂直，记作l⊥.直线l叫做平面的垂线，平面叫做直线l的垂面.直线与平面垂直时，它们惟一的公共点P叫做垂足.‎ 画直线与平面垂直时，通常把直线画成与表不平面的平行四边形的一边垂直，如图. ‎ 师：日常生活中我们对直线与平面垂直有很多感性认识，如旗杆与地面，桥柱与水面等，你能举出更多的例子来吗？‎ 师：在阳光下观察，直立于地面的旗杆及它在地面的影子，它们的位置关系如何？‎ 生：旗杆与地面内任意一条经B的直线垂直.‎ 师：那么旗杆所在直线与平面内不经过B点的直线位置关系如何，依据是什么？（图）‎ 生：垂直，依据是异面直线垂直的定义.‎ 师：你能尝试给线面垂直下定义吗？‎ ‎……‎ 师：能否将任意直线改为无数条直线？学生找一反例说明.‎ 培养学生的几何直观能力使他们在直观感知，操作确认的基础上学会归纳概括结论.‎ 探索新知 二、直线和平面垂直的判定 ‎1．试验 如图，过△ABC的顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触）.‎ ‎（1）折痕AD与桌面垂直吗？‎ ‎（2）如何翻折才能使折痕AD与桌面所在平面垂直？‎ ‎2．直线与平面垂直的判定定理：‎ 一条直线与一个平面内两条相交直线都垂直，则该直线与此平面垂直.‎ 思考：能否将直线与平面垂直的判定定理中的“两条相交直线”改为一条直线或两条平行直线？‎ 师：下面请同学们准备一块三角形的小纸片，我们一起来做一个实验，（投影问题）.‎ 学生动手实验，然后回答问题.‎ 生：当且仅当折痕AD是BC边上的高时，AD所在直线与桌面所在平面垂直.‎ 师：此时AD垂直上的一条直线还是两条直线？‎ 生：AD垂直于桌面两条直线，而且这两条直线相交.‎ 师：怎么证明？‎ 生：折痕AD⊥BC，翻折之后垂直关系不变，即AD⊥CD，AD⊥BD ‎……‎ 师：直线和平面垂直的判定定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.‎ 培养学生的几何直观能力使他们在直观感知，操作确认的基础上学会归纳概括结论.‎ 典例剖析 例1 如图，已知a∥b，a⊥，求证：b⊥.‎ 证明：在平面内作两条相交直线m、n.‎ 因为直线a⊥，根据直线与平面垂直的定义知 a⊥m，a⊥n.‎ 又因为b∥a，‎ 所以b⊥m，b⊥n.‎ 又因为，m、n是两条相交直线，‎ b⊥.‎ 师：要证b⊥，需证b与内任意一条直线的垂直，又a∥b，问题转化为a与面内任意直线m垂直，这个结论显然成立.‎ 学生依图及分析写出证明过程.‎ ‎……‎ 师：此结论可以直接利用，判定直线和平面垂直.‎ 巩固所知识培养学生转化化归能力、书写表达能力.‎ 探索新知 二、直线和平面所成的角 如图，一条直线PA和一个平面相交，但不与这个平面垂直，这条直线叫做这个平面的斜线，斜线的平面的交点A叫做斜足.过斜线上斜足以外的一点向平面引垂线 教师借助多媒体直接讲授，注意直线和平面所成的角是分三种情况定义的.‎ 借助多媒体讲授，提高上课效率.‎ PO，过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角.‎ 一条直线垂直于平面，我们说它们所成的角是直角；一条直线和平面平行，或在平面内，我们说它们所成的角是0°的角.‎ 典例剖析 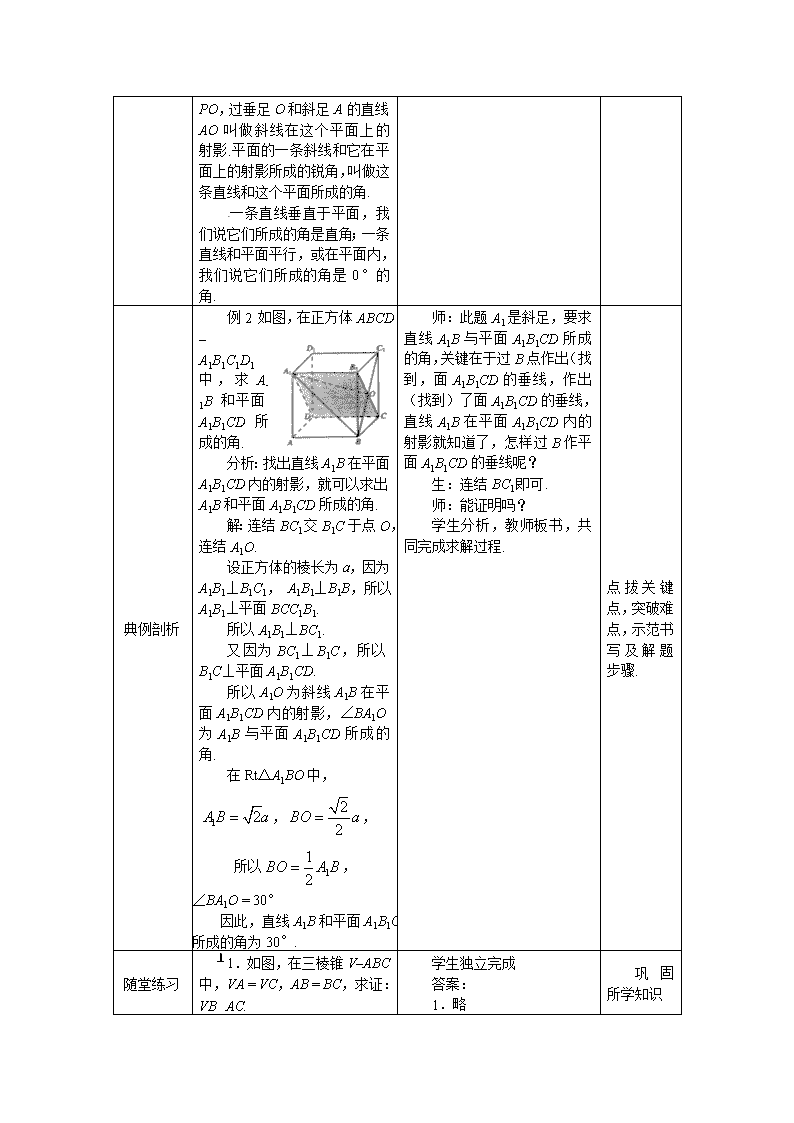例2 如图，在正方体ABCD – A1B‎1C1D1中，求A1B和平面A1B1CD所成的角.‎ 分析：找出直线A1B在平面A1B1CD内的射影，就可以求出A1B和平面A1B1CD所成的角.‎ 解：连结BC1交B‎1C于点O，连结A1O.‎ 设正方体的棱长为a，因为A1B1⊥B‎1C1， A1B1⊥B1B，所以A1B1⊥平面BCC1B1.‎ 所以A1B1⊥BC1.‎ 又因为BC1⊥B‎1C，所以B‎1C⊥平面A1B1CD.‎ 所以A1O为斜线A1B在平面A1B1CD内的射影，∠BA1O为A1B与平面A1B1CD所成的角.‎ 在Rt△A1BO中，‎ ‎，，‎ 所以，‎ ‎∠BA1O = 30°‎ ‎ 因此，直线A1B和平面A1B1CD所成的角为30°.‎ 师：此题A1是斜足，要求直线A1B与平面A1B1CD所成的角，关键在于过B点作出（找到，面A1B1CD的垂线，作出（找到）了面A1B1CD的垂线，直线A1B在平面A1B1CD内的射影就知道了，怎样过B作平面A1B1CD的垂线呢？‎ 生：连结BC1即可.‎ 师：能证明吗？‎ 学生分析，教师板书，共同完成求解过程.‎ 点拔关键点，突破难点，示范书写及解题步骤.‎ 随堂练习 ‎1．如图，在三棱锥V–ABC中，VA = VC，AB = BC，求证：VB⊥AC.‎ 学生独立完成 答案：‎ ‎1．略 巩固所学知识 ‎2．过△ABC所在平面外一点P，作PO⊥，垂足为O，连接PA ，PB，PC.‎ ‎（1）若PA= PB = PC，∠C =90°，则点O是AB边的 心.‎ ‎（2）若PA = PB =PC，则点O是△ABC的 心.‎ ‎（3）若P A⊥PB，PB⊥PC，PB⊥P A，则点O是△ABC的 . 心.‎ ‎3．两条直线和一个平面所成的角相等，这两条直线一定平行吗？‎ ‎4．如图，直四棱柱A′B′C′D′ – ABCD（侧棱与底面垂直的棱柱称为直棱柱）中，底面四边形ABCD满足什么条件时，A′C⊥B′D′？‎ ‎2．（1）AB边的中点；（2）点O是△ABC的外心；（3）点O是△ABC的垂心.‎ ‎3．不一定平行.‎ ‎4．AC⊥BD.‎ 归纳总结 ‎1．直线和平面垂直的定义判定 ‎2．直线和平面所成的角定义与解答步骤、完善.‎ ‎3．线线垂直线面垂直 学生归纳总结教师补充 巩固学习成果，使学生逐步养成爱总结，会总结的习惯和能力.‎ 课后作业 ‎2.7 第一课时 习案 学生独立完成 强化知识 提升能力 备选例题 例1 如图，在空间四边形ABCD中，AB = AD，CB = CD，M为BD中点，作AO⊥MC，交MC于O．求证：AO⊥平面BCD．‎ ‎【解析】连结AM ‎∵AB = AD，CB = CD，M为BD中点．‎ ‎∴BD⊥AM，BD⊥CM．‎ 又AM∩CM = M，∴BD⊥平面ACM．‎ ‎≠‎ ‎≠‎ ‎∵AO 平面ACM，∴BD⊥AO．‎ 又MC⊥AO，BD∩MC = M，∴AO⊥平面貌BCD．‎ ‎【评析】本题为了证明AO⊥平面BCD，先证明了平面BCD内的直线垂直于AO所在的平面．这一方法具有典型性，即为了证明线与面的垂直，需要转化为线与线的垂直；为了解决线与线的垂直，又需转化为另一个线与面的垂直，再化为新的线线垂直．这样互相转化，螺旋式往复，最终使问题得到解决．‎ 例2 已知棱长为1的正方体ABCD – A1B‎1C1D1中，E是A1B1的中点，求直线AE与平面ABC1D1所成的角的正弦值．‎ ‎【解析】取CD的中点F，连接EF交平面ABC1D1于O，连AO．‎ 由已知正方体，易知EO⊥ABC1D1，所以∠EAO为所求．‎ 在Rt △EOA中，‎ ‎ ，‎ ‎，‎ sin∠EAO = ．‎ 所以直线AE与平面ABC1D1所成的角的正弦值为．‎ ‎【评析】求直线和平面所成角的步骤：‎ ‎（1）作——作出斜线和平面所成的角；‎ ‎（2）证——证明所作或找到的角就是所求的角；‎ ‎（3）求——常用解三角形的方法（通常是解由垂线、斜线、射影所组成的直角形）‎ ‎（4）答．‎