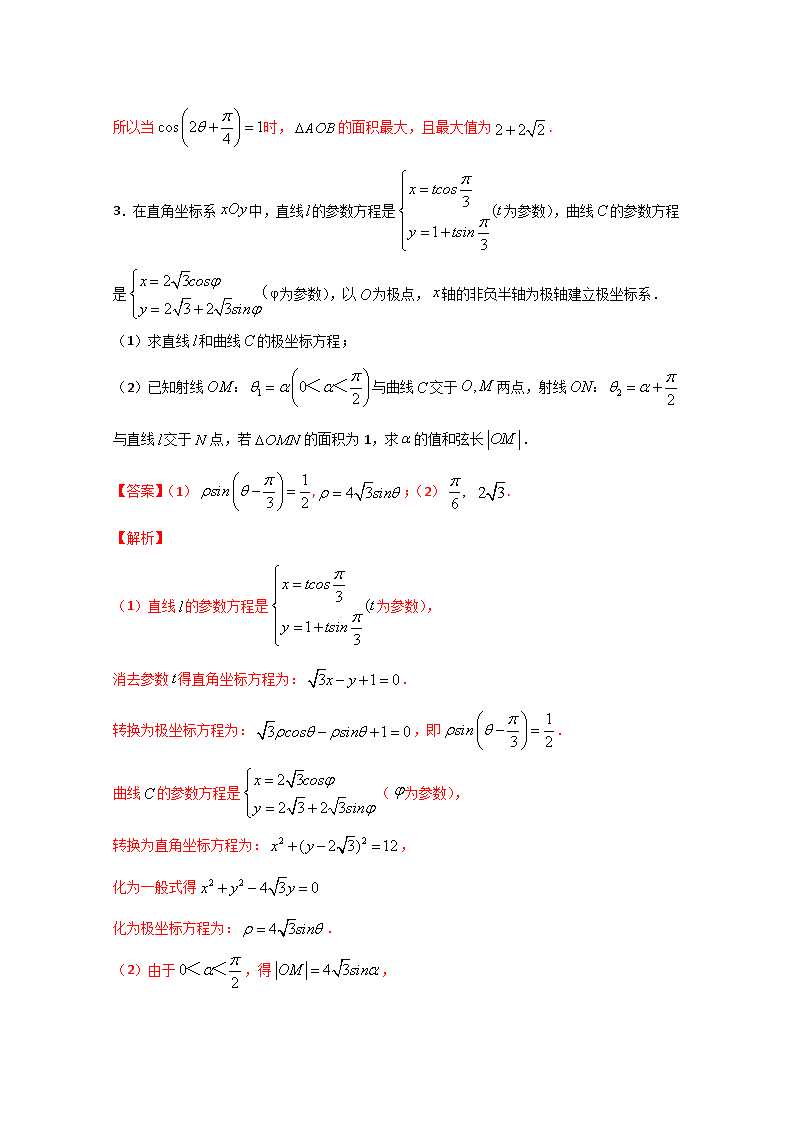第13章 参数方程与极坐标 检测B卷-2020年领军高考数学一轮复习（文理通用） Word版含解析 19页

‎2020年领军高考数学一轮复习(文理通用)‎ 选修系列—坐标系与参数方程 章节验收测试卷B卷 姓名 班级 准考证号 ‎ ‎ 1．在平面真角坐标系xOy中，曲线的参数方程为（t为参数），以原点O为极点，x轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为．‎ ‎（1）求曲线的普通方程和曲线的直角坐标方程；‎ ‎（2）若曲线与曲线交于M，N两点，直线OM和ON的斜率分别为和，求的值．‎ ‎【答案】（1），（2）1‎ ‎【解析】‎ ‎（1）．由，（t为参数），消去参数t，得，即的普通方程为，由，得，即，‎ 将代入，得，即的直角坐标方程为．‎ ‎（2）．由（t为参数），得，则的几何意义是抛物线上的点（原点除外）与原点连线的斜率．由题意知，‎ 将，（t为参数）代入，得．‎ 由，且得，且．‎ 设M，N对应的参数分别为、，则，，‎ 所以． 2．在直角坐标系中，曲线的参数方程为 （为参数），以坐标原点 为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，且曲线与恰有一个公共点.‎ ‎(Ⅰ)求曲线的极坐标方程；‎ ‎(Ⅱ)已知曲线上两点，满足，求面积的最大值.‎ ‎【答案】(Ⅰ) .(Ⅱ) .‎ ‎【解析】‎ ‎(Ⅰ)曲线的极坐标方程为，‎ 将代入上式可得直角坐标方程为，‎ 即，所以曲线为直线．‎ 又曲线是圆心为,半径为的圆，‎ 因为圆与直线恰有一个公共点，‎ 所以，‎ 所以圆的普通方程为，‎ 把代入上式可得的极坐标方程为，‎ 即.‎ ‎(Ⅱ)由题意可设，‎ ‎ ‎ ‎ ‎ ‎，‎ 所以当时，的面积最大，且最大值为. 3．在直角坐标系中，直线的参数方程是为参数），曲线的参数方程是为参数），以为极点，轴的非负半轴为极轴建立极坐标系．‎ ‎（1）求直线和曲线的极坐标方程；‎ ‎（2）已知射线与曲线交于两点，射线与直线交于点，若的面积为1，求的值和弦长．‎ ‎【答案】（1）,；（2） .‎ ‎【解析】‎ ‎（1）直线的参数方程是为参数），‎ 消去参数得直角坐标方程为：．‎ 转换为极坐标方程为：，即．‎ 曲线的参数方程是（为参数），‎ 转换为直角坐标方程为：， ‎ 化为一般式得 化为极坐标方程为：．   ‎ ‎（2）由于，得，‎ ‎．‎ 所以，‎ 所以，‎ 由于，所以，‎ 所以． 4．在平面直角坐标系中,直线的参数方程为 (为参数),曲线的参数方为 (为参数),以为极点, 轴的非负半轴为极轴建立极坐标系.‎ ‎(1)求直线和曲线的极坐标方程;‎ ‎(2)设,,为直线与曲线的两个交点,求的最大值.‎ ‎【答案】（1） ，（2）4‎ ‎【解析】‎ ‎（1）直线的极坐标方程为（）； ‎ 曲线的普通方程为， ‎ 因为，，，‎ 所以曲线的极坐标方程为. ‎ ‎（2）设，且，‎ 将代入曲线的极坐标方程，有 ‎， ‎ 因为，‎ ‎，‎ 根据极坐标的几何意义，分别表示点的极径，‎ 因此， ‎ 因为，所以，‎ 所以，当，即时，取最大值. 5．在平面直角坐标系中，曲线过点，其参数方程为（为参数，）.以为极点，轴非负半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求曲线的普通方程和曲线的直角坐标方程；‎ ‎（2）已知曲线与曲线交于两点，且，求实数的值.‎ ‎【答案】(1) ;.(2) 或.‎ ‎【解析】‎ ‎（1）曲线参数方程为为参数，消去参数，得，‎ ‎∴曲线的普通方程，‎ 又由曲线的极坐标方程为，∴，‎ 根据极坐标与直角坐标的互化公式，代入得，‎ 整理得，即曲线的直角坐标方程.‎ ‎（2）设两点所对应参数分别为，，‎ 将代入，得，‎ 要使与有两个不同的交点，则，即，‎ 由韦达定理有，根据参数的几何意义可知，，‎ 又由，可得，即或，‎ ‎∴当时，有，符合题意.‎ 当时，有，符合题意.‎ 综上所述，实数的值为或. 6．在平面直角坐标系xOy中，曲线的参数方程为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线 是圆心的极坐标为（）且经过极点的圆 ‎（1）求曲线C1的极坐标方程和C2的普通方程；‎ ‎（2）已知射线分別与曲线C1，C2交于点A，B（点B异于坐标原点O），求线段AB的长 ‎【答案】(1) ;.(2) .‎ ‎【解析】‎ ‎（1）由曲线的参数方程为（为参数），消去参数得，‎ 又代入得的极坐标方程为，‎ 由曲线是圆心的极坐标为且经过极点的圆.‎ 可得其极坐标方程为，‎ 从而得的普通方程为.‎ ‎（2）将代入得，‎ 又将代入得，‎ 故. 7．在平面直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为（1+cos2θ）=8sinθ．‎ ‎（1）求曲线C的普通方程；‎ ‎（2）直线l的参数方程为,t为参数直线与y轴交于点F与曲线C的交点为A，B，当|FA|•|FB|取最小值时，求直线的直角坐标方程．‎ ‎【答案】（1）x2=4y；（2）y=1‎ ‎【解析】‎ ‎（1）由题意得ρ（1+cos2θ）=8sinθ，得2ρcos2θ=8sinθ，得ρ2cos2θ=4ρsinθ，‎ ‎∵x=ρcosθ，y=ρsinθ，∴x2=4y，即曲线C的普通方程为x2=4y．‎ ‎（2）由题意可知，直线与y轴交于点F（0，1）即为抛物线C的焦点，‎ 令|FA|=|t1|，|FB|=|t2|，将直线的参数方程代入C的普通方程x2=4y中，‎ 整理得t2cos2α-4tsinα-4=0，‎ 由题意得cosα≠0，根据韦达定理得：t1+t2=，t1t2=，‎ ‎∴|FA||FB|=|t1||t2|=|t1t2|=≥4，（当且仅当cos2α=1时，等号成立），‎ ‎∴当|FA|•|FB|取得最小值时，直线的直角坐标方程为y=1． 8．在直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的参数方程为为参数）．‎ ‎（1）写出的普通方程，求的极坐标方程；‎ ‎（2）若过原点的直线与相交于两点，中点的极坐标为，求的直角坐标．‎ ‎【答案】（1），；（2）.‎ ‎【解析】‎ ‎（1）C的普通方程,‎ ‎∴‎ C的极坐标方程；‎ ‎（2）由已知得直线l的极坐标方程为 代入 得 ‎ ‎∴ ，设则 ‎∵D是AB中点 ‎∴‎ ‎∴‎ ‎∴D的直角坐标为． 9．在同一直角坐标系中，经过伸缩变换后，曲线C的方程变为.以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线/的极坐标方程为.‎ ‎（1）求曲线C和直线l的直角坐标方程；‎ ‎（2）过点作l的垂线l0交C于A，B两点，点A在x轴上方，求的值.‎ ‎【答案】（1），（2）‎ ‎【解析】‎ ‎（1）将代入得，曲线C的方程为，‎ 由，得，‎ 把，代入上式得直线l的直角坐标方程为. ‎ ‎（2）因为直线l的倾斜角为，所以其垂线l0的倾斜角为，‎ 则直线l0的参数方程为（t为参数），即（t为参数）‎ 代入曲线C的方程整理得，‎ 设A，B两点对应的参数为t1，t2，由题意知，，‎ 则，且，‎ 所以. 10．在平面直角坐标系中，直线的参数方程为（为参数）.以原点为极点，轴的正半轴为极轴建立极坐标系，且曲线的极坐标方程为.‎ ‎（1）写出直线的普通方程与曲线的直角坐标方程；‎ ‎（2）设直线上的定点在曲线外且其到上的点的最短距离为，试求点的坐标.‎ ‎【答案】（1）的普通方程为．的直角坐标方程为 （2）（-1，0）或（2，3）‎ ‎【解析】‎ ‎（1）由消去参数，得．‎ 即直线的普通方程为． ‎ 因为 又，‎ ‎∴曲线的直角坐标方程为 ‎ ‎（2）由知，曲线C是以Q（1,1）为圆心，为半径的圆 设点P的坐标为，则点P到上的点的最短距离为|PQ|‎ 即，整理得，解得 ‎ 所以点P的坐标为（-1，0）或（2，3） 11．在直角坐标系中，直线的参数方程为（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为 ‎（1）求曲线的直角坐标方程；‎ ‎（2）设直线与曲线交于，两点，求线段的长 ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎（1）的方程可化为，将，，代入其中 得，所以曲线的直角坐标方程为.‎ ‎（2）直线过定点，将直线的参数方程代入曲线的直角坐标方程得，，，‎ 所以 . 12．在平面直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴的非负半轴为极轴且取相同的单位长度建立极坐标系，直线的极坐标方程为（）.‎ ‎（1）写出直线的直角坐标方程与曲线的普通方程；‎ ‎（2）平移直线使其经过曲线的焦点，求平移后的直线的极坐标方程.‎ ‎【答案】(1) ，；(2) 或.‎ ‎【解析】‎ ‎（1）直线的极坐标方程为化为直角坐标方程是.‎ 由（为参数）得，‎ 所以曲线的普通方程是.‎ ‎（2）因为直线的斜率是1，‎ 所以平移后的直线的斜率仍然是1. ‎ 因为曲线的焦点坐标是，， ‎ 所以当平移后的直线经过焦点时，直线方程是，即， ‎ 化为极坐标方程是； ‎ 当平移后的直线经过焦点时，直线方程是，即，‎ 化为极坐标方程是. 13．在直角坐标系中，曲线的参数方程为（为参数），直线的方程为．‎ ‎（1）以坐标原点为极点，轴的正半轴为极轴建立极坐标系，求曲线的极坐标方程和直线的极坐标方程；‎ ‎（2）在（1）的条件下，直线的极坐标方程为，设曲线与直线的交于点和点，曲线与直线的交于点和点，求的面积．‎ ‎【答案】（1）极坐标方程为：.直线的极坐标方程为：．（2）‎ ‎【解析】‎ ‎（1）由，‎ 得曲线C的普通方程为， ‎ 把，代入该式化简得曲线C的极坐标方程为：. ‎ 因为直线：是过原点且倾斜角为的直线，‎ 所以直线的极坐标方程为：． ‎ ‎（2）把代入得，故，‎ 把代入得，故， ‎ 因为, ‎ 所以的面积为. 14．已知曲线的极坐标方程为，曲线的参数方程为（为参数），曲线的参数方程为（为参数）.‎ ‎（Ⅰ）若曲线与无公共点，求正实数的取值范围；‎ ‎（Ⅱ）若曲线的参数方程中，，且曲线与交于，两点，求.‎ ‎【答案】(1) .(2)8.‎ ‎【解析】‎ ‎（Ⅰ）的直角坐标方程为①，‎ 的直角坐标方程为②，‎ 将①②联立，可求得，‎ 由题意:，求得. ‎ ‎（II）当时，曲线为直线，‎ 解方程组，得，，‎ 所以易得. 15．以平面直角坐标系xOy的原点为极点，x轴的正半轴为极轴，取相同的长度单位建立极坐标系，直线l的坐标方程为，曲线C的参数方程为（θ为参数）．‎ ‎（1）求直线l的直角坐标方程和曲线C的普通方程；‎ ‎（2）以曲线C上的动点M为圆心、r为半径的圆恰与直线l相切，求r的最小值．‎ ‎【答案】（1），；（2）.‎ ‎【解析】‎ ‎（1）由，‎ 得，‎ 将，代入上式，‎ 得直线的直角坐标方程为.‎ 由曲线的参数方程（为参数），‎ 得曲线的普通方程为.‎ ‎（2）设点的坐标为，‎ 则点到直线的距离为 ‎ （其中 当时，圆与直线相切，‎ 故当时，取最小值，‎ 且的最小值为. ‎ ‎16．以坐标原点为极点，以轴正半轴为极轴，建立的极坐标系中，直线；在平面直角坐标系中，曲线（为参数，）.‎ ‎（1）求直线的直角坐标方程和曲线的极坐标方程；‎ ‎（2）曲线的极坐标方程为 ，且曲线分别交，于，两点，若，求的值.‎ ‎【答案】（1）,；（2）.‎ ‎【解析】‎ ‎（1），即.‎ 由，消去参数得的普通方程：.‎ 又，的极坐标方程为：.‎ 即的极坐标方程为.‎ ‎（2）曲线的直角坐标方程为 ，由，得.‎ ‎，.即点B的极坐标为代入，得. 17．在平面直角坐标系中，已知曲线的参数方程为（为参数），以原点为极点，轴的非负半轴为极轴建立极坐标系.‎ ‎（1）求曲线的极坐标方程；‎ ‎（2）过点倾斜角为的直线与曲线交于两点，求的值.‎ ‎【答案】（1）;（2）8.‎ ‎【解析】‎ ‎（1）依题意，曲线的普通方程为，‎ 即，故，故，‎ 故所求极坐标方程为；‎ ‎（2）设直线的参数方程为（为参数），‎ 将此参数方程代入中，‎ 化简可得，‎ 显然.设所对应的参数分别为，，则.‎ ‎∴. 18．已知平面直角坐标系，直线过点，且倾斜角为，以为极点，轴的非负半轴为极轴建立极坐标系，圆的极坐标方程为.‎ ‎（1）求直线的参数方程和圆的标准方程；‎ ‎（2）设直线与圆交于、两点，若，求直线的倾斜角的值.‎ ‎【答案】（1）直线的参数方程为（为参数），圆的标准方程为：.（2）或.‎ ‎【解析】‎ ‎（1）因为直线过点，且倾斜角为，‎ 所以直线的参数方程为（为参数），‎ 因为圆的极坐标方程为，‎ 所以，‎ 所以圆的普通方程为：，‎ 圆的标准方程为：.‎ ‎（2）直线的参数方程为，代入圆的标准方程得，‎ 整理得，‎ 设、两点对应的参数分别为、，则恒成立， ，=-4<0‎ 所以，.‎ 因为，所以或. 19．在直角坐标系中，曲线的参数方程为，（为参数，且，）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求的普通方程和的直角坐标方程；‎ ‎（2）若与的交点为，且，求.‎ ‎【答案】（1）,；（2）1.‎ ‎【解析】‎ ‎（1）利用消去参数， ‎ 得的普通方程为. ‎ 由得，将 代入上式并整理得的直角坐标方程为. ‎ ‎（2）根据对称性知，和关于轴对称，‎ 不妨设，，，‎ 因为，所以， ‎ 代入的直角坐标方程得， ‎ 又在上，所以， ‎ 解得a=1. 20．在平面直角坐标系中，直线的方程为，圆的参数方程为（为参数）.以为极点，轴的非负半轴为极轴建立极坐标系，圆的极坐标方程为.‎ ‎（1）求的极坐标方程；‎ ‎（2）设与，异于原点的交点分别是，求的面积.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎（1）由 得，‎ 化为.‎ 即.‎ 因为，，‎ 所以的极坐标方程为.‎ ‎（2）因为直线的斜率为，即倾斜角为，‎ 所以其极坐标方程为.‎ 设，.‎ 由，‎ 得，‎ 即，‎ 由，‎ 得，‎ 即.‎ 由的极坐标方程得，‎ 所以，‎ ‎.‎ 因为，‎ 所以的面积为.‎