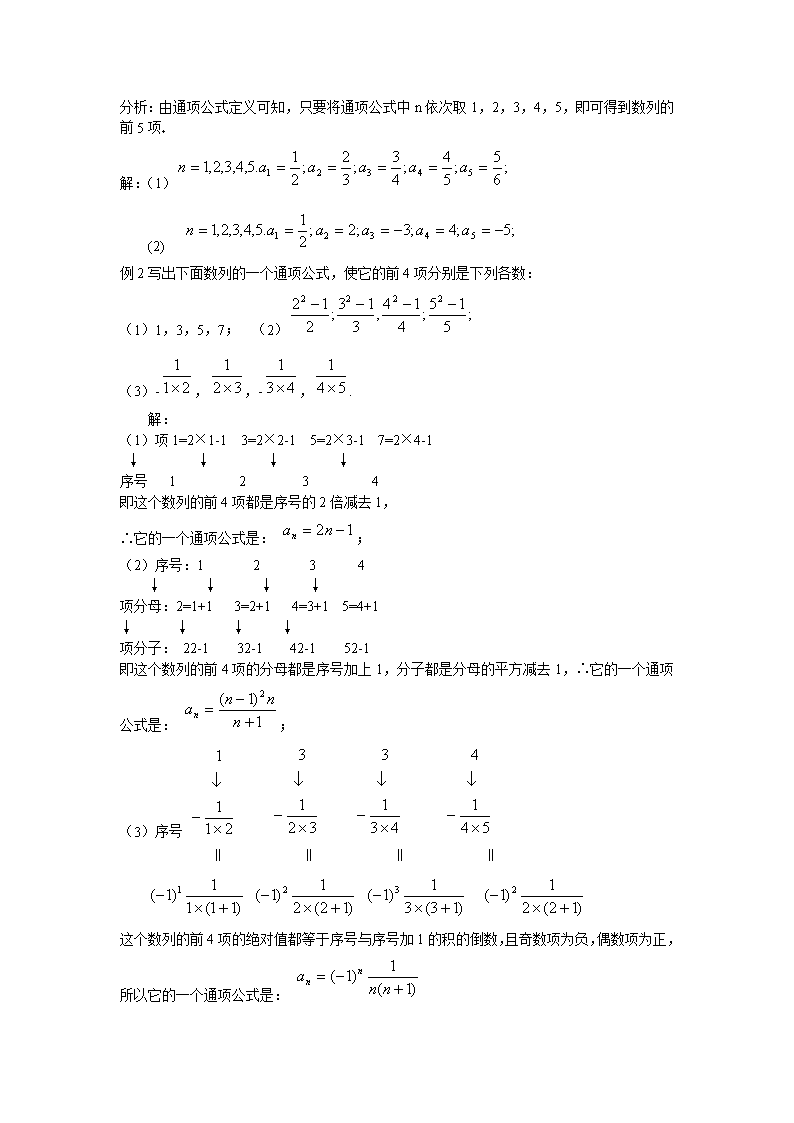高中数学必修5教案：2_1数列的概念 19页

第二章数列 课题 §‎2.1.1‎数列的概念与简单表示法 授课类型：新授课 ‎（第1课时）‎ ‎●教学目标 知识与技能：理解数列及其有关概念，了解数列和函数之间的关系；了解数列的通项公式，并会用通项公式写出数列的任意一项；对于比较简单的数列，会根据其前几项写出它的个通项公式。‎ 过程与方法：通过对一列数的观察、归纳，写出符合条件的一个通项公式，培养学生的观察能力和抽象概括能力．‎ 情感态度与价值观：通过本节课的学习，体会数学来源于生活，提高数学学习的兴趣 ‎●教学重点 数列及其有关概念，通项公式及其应用 ‎●教学难点 根据一些数列的前几项抽象、归纳数列的通项公式 ‎●教学过程 Ⅰ.课题导入 ‎4，5，6，7，8，9，10． ①‎ ‎1，，，，，…. ②‎ ‎1，0.1，0.01，0.001，0.0001，…. ③‎ ‎1，1.4，1.41，1.414，…. ④‎ ‎-1，1，-1，1，-1，1，…. ⑤‎ ‎2，2，2，2，2，…. ⑥‎ 观察这些例子，看它们有何共同特点？（启发学生发现数列定义）‎ 上述例子的共同特点是：⑴均是一列数；⑵有一定次序. ‎ 从而引出数列及有关定义 ‎ Ⅱ.讲授新课 ‎⒈ 数列的定义：按一定次序排列的一列数叫做数列.‎ 注意：⑴数列的数是按一定次序排列的，因此，如果组成两个数列的数相同而排列次序不同，那么它们就是不同的数列；‎ ‎⑵定义中并没有规定数列中的数必须不同，因此，同一个数在数列中可以重复出现.‎ ‎⒉ 数列的项：数列中的每一个数都叫做这个数列的项. 各项依次叫做这个数列的第1项（或首项），第2项，…，第n 项，….‎ 例如，上述例子均是数列，其中①中，“4”是这个数列的第1项（或首项），“9”是这个数列中的第6项.‎ ‎⒊数列的一般形式：，或简记为，其中是数列的第n项 结合上述例子，帮助学生理解数列及项的定义. ②中，这是一个数列，它的首项是“1”，“”是这个数列的第“3”项，等等 下面我们再来看这些数列的每一项与这一项的序号是否有一定的对应关系？这一关系可否用一个公式表示？（引导学生进一步理解数列与项的定义，从而发现数列的通项公式）对于上面的数列②，第一项与这一项的序号有这样的对应关系：‎ 项 ‎ ‎↓ ↓ ↓ ↓ ↓‎ 序号 1 2 3 4 5‎ 这个数的第一项与这一项的序号可用一个公式：来表示其对应关系 即：只要依次用1，2，3…代替公式中的n，就可以求出该数列相应的各项 结合上述其他例子，练习找其对应关系 ‎⒋ 数列的通项公式：如果数列的第n项与n之间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的通项公式.‎ 注意：⑴并不是所有数列都能写出其通项公式，如上述数列④；‎ ‎⑵一个数列的通项公式有时是不唯一的，如数列：1，0，1，0，1，0，…它的通项公式可以是，也可以是.‎ ‎⑶数列通项公式的作用：①求数列中任意一项；②检验某数是否是该数列中的一项.‎ 数列的通项公式具有双重身份，它表示了数列的第 项，又是这个数列中所有各项的一般表示．通项公式反映了一个数列项与项数的函数关系，给了数列的通项公式，这个数列便确定了，代入项数就可求出数列的每一项．‎ ‎5.数列与函数的关系 数列可以看成以正整数集N*（或它的有限子集{1，2，3，…，n}）为定义域的函数，当自变量从小到大依次取值时对应的一列函数值。‎ 反过来，对于函数y=f(x),如果f(i)（i=1、2、3、4…）有意义，那么我们可以得到一个数列f(1)、 f(2)、 f(3)、 f(4)…，f(n)，…‎ ‎6．数列的分类：‎ ‎1）根据数列项数的多少分：‎ 有穷数列：项数有限的数列.例如数列1，2，3，4，5，6。是有穷数列 无穷数列：项数无限的数列.例如数列1，2，3，4，5，6…是无穷数列 ‎2）根据数列项的大小分：‎ 递增数列：从第2项起，每一项都不小于它的前一项的数列。‎ 递减数列：从第2项起，每一项都不大于它的前一项的数列。‎ 常数数列：各项相等的数列。‎ 摆动数列：从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列 ‎ [范例讲解] 例1 根据下面数列的通项公式，写出前5项：‎ ‎（1）‎ 分析：由通项公式定义可知，只要将通项公式中n依次取1，2，3，4，5，即可得到数列的前5项 解：（1）‎ ‎ (2) ‎ 例2写出下面数列的一个通项公式，使它的前4项分别是下列各数：‎ ‎（1）1，3，5，7； （2）‎ ‎（3）-，，-，.‎ ‎ 解：‎ ‎（1）项1=2×1-1 3=2×2-1 5=2×3-1 7=2×4-1‎ ‎ ↓ ↓ ↓ ↓ ‎ 序号 1 2 3 4‎ 即这个数列的前4项都是序号的2倍减去1，‎ ‎∴它的一个通项公式是： ；‎ ‎（2）序号：1 2 3 4‎ ‎ ↓ ↓ ↓ ↓ ‎ 项分母：2=1+1 3=2+1 4=3+1 5=4+1‎ ‎↓ ↓ ↓ ↓ ‎ 项分子： 22-1 32-1 42-1 52-1‎ 即这个数列的前4项的分母都是序号加上1，分子都是分母的平方减去1，∴它的一个通项公式是： ； ‎ ‎（3）序号 ‎ ‎ ‖ ‖ ‖ ‖‎ ‎ ‎ 这个数列的前4项的绝对值都等于序号与序号加1的积的倒数，且奇数项为负，偶数项为正，所以它的一个通项公式是： ‎ Ⅲ.课堂练习 课本[练习]3、4、5‎ ‎[补充练习]：根据下面数列的前几项的值，写出数列的一个通项公式：‎ ‎(1) 3, 5, 9, 17, 33,……； (2) , , , , , ……；‎ ‎ (3) 0, 1, 0, 1, 0, 1,……； (4) 1, 3, 3, 5, 5, 7, 7, 9, 9, ……；‎ ‎(5) 2, －6, 12, －20, 30, －42,…….‎ ‎ 解：(1) ＝2n＋1； (2) ＝； (3) ＝； ‎ ‎(4) 将数列变形为1＋0, 2＋1, 3＋0, 4＋1, 5＋0, 6＋1, 7＋0, 8＋1, ……, ‎ ‎∴＝n＋；‎ ‎(5) 将数列变形为1×2, －2×3, 3×4, －4×5, 5×6,……，‎ ‎∴ ＝(－1)n(n＋1)‎ Ⅳ.课时小结 本节课学习了以下内容：数列及有关定义，会根据通项公式求其任意一项，并会根据数列的前n项求一些简单数列的通项公式。‎ Ⅴ.课后作业 课本习题‎2.1A组的第1题 ‎§‎2.1.1‎数列的概念与简单表示法 ‎【课前预习】‎ ‎1、在数列1，1，2，3，5，8，13，x，34，55，…中，x的值是　‎ A、19 　　 B、 ‎20 ‎‎ ‎ 　 C、 21 D 、22‎ ‎2、观察下面数列的特点，用适当的数填空 ‎（1） ，，，， ； ‎ ‎（2），， ，，， 。‎ ‎3 .已知数列，，则 .‎ ‎4 根据下列数列的前几项的值，写出它的一个通项公式。‎ ‎（1）数列0.7,0.77,0.777,0.7777,…的一个通项公式为 .‎ ‎（2）数列4,0,4,0,4,0,…的一个通项公式为 .‎ ‎（3）数列的一个通项公式为 .‎ ‎5.已知数列满足，，则 .‎ ‎1 C‎ 2 （1）1， （2） 3.29 ‎ ‎4. （1）an=;（2）an=2+2·(-1)n+1 （3） 5.‎ ‎【课内探究】‎ ‎1 展示三角形数、正方形数，提问：这些数有什么规律？与它所表示的图形的序号有什么关系？‎ ‎（1）概括数列的概念：按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项。‎ ‎（2）辩析数列的概念：“1，2，3，4，‎5”‎与“5，4，3，2，‎1”‎是同一个数列吗？与“1，3，2，4，‎5”‎呢？给出首项与第n 项的定义及数列的记法：{an}‎ ‎（3）数列的分类: 有穷数列与无穷数列；递增数列与递减数列，常数列。‎ ‎3 数列的表示方法 ‎（1）函数y=7x+9 与y=3 x ，当依次取1，2，3，…时，其函数值构成的数列各有什么特点？‎ ‎（2）定义数列{an}的通项公式 ‎（3）数列{an}的通项公式可以看成数列的函数解析式，利用一个数列的通项公式，你能确定这个数列的哪些方面的性质？‎ ‎（4）用列表和图象等方法表示数列，数列的图象是一系列孤立的点。‎ ‎4、例1 写出下面数列的一个通项公式，使它的前4项分别是下列各数：‎ ‎ （1）1，-1/2，1/3，-1/4；‎ ‎ （2）2，0，2，0．‎ ‎【课后提高】‎ ‎1.数列1，2，2，3，3，3，4，4，4，4，5，…的第100项是 .‎ ‎2.数列{an}中，a1=1,对于所有的n≥2，n∈N*都有a1·a2·a3·…·an=n2，则a3+a5= .‎ ‎3.数列-1,，-，，…的一个通项公式是 .‎ ‎4.下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案，则按此规律第n个图案中需用黑色瓷砖 块.（用含n的代数式表示）‎ ‎5.若数列{an}的通项公式an=，记f（n）=2(1-a1)(1-a2)…(1-an)，试通过计算f(1),f(2),f(3)的值，推测出f(n)= (用含n的代数式表示）.‎ ‎6.根据下面各数列前几项的值，写出数列的一个通项公式：‎ ‎（1），，，，，…‎ ‎（2），2，，8，，…‎ ‎（3）5，55，555，5 555，55 555，…‎ ‎（4）5，0，-5，0，5，0，-5，0，…‎ ‎（5）1，3，7，15，31，…‎ ‎（3）联想=10n-1,‎ 则an===(10n-1),‎ 即an= (10n-1).‎ ‎（4）数列的各项都具有周期性，联想基本数列1，0，-1，0，…，‎ 则an=5sin.‎ ‎（5）∵1=2-1，3=22-1，7=23-1，…‎ ‎∴an=2n-1‎ 故所求数列的通项公式为an=2n-1.‎ 学校：二中 学科：数学 编写人：赵云雨 一审：李其智 二审：马英济 课题 ‎ ‎§‎2.1.2‎数列的概念与简单表示法 授课类型：新授课 ‎（第２课时）‎ ‎●教学目标 知识与技能：了解数列的递推公式，明确递推公式与通项公式的异同；会根据数列的递推公式写出数列的前几项；理解数列的前n项和与的关系 过程与方法：经历数列知识的感受及理解运用的过程。‎ 情感态度与价值观：通过本节课的学习，体会数学来源于生活，提高数学学习的兴趣。‎ ‎●教学重点 根据数列的递推公式写出数列的前几项 ‎●教学难点 理解递推公式与通项公式的关系 ‎●教学过程 Ⅰ.课题导入 ‎[复习引入]‎ 数列及有关定义 Ⅱ.讲授新课 数列的表示方法 通项公式法 如果数列的第n项与序号之间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的通项公式。‎ 如数列 的通项公式为 ；‎ ‎   的通项公式为 ；‎ ‎　　 的通项公式为 ；‎ 图象法 启发学生仿照函数图象的画法画数列的图形．具体方法是以项数 为横坐标，相应的项 为纵坐标，即以 为坐标在平面直角坐标系中做出点（以前面提到的数列 为例，做出一个数列的图象），所得的数列的图形是一群孤立的点，因为横坐标为正整数，所以这些点都在 轴的右侧，而点的个数取决于数列的项数．从图象中可以直观地看到数列的项随项数由小到大变化而变化的趋势．‎ 递推公式法 知识都来源于实践，最后还要应用于生活用其来解决一些实际问题．‎ ‎ 观察钢管堆放示意图，寻其规律，建立数学模型．‎ ‎ 模型一：自上而下：‎ ‎ 第1层钢管数为4；即：14＝1+3‎ ‎ 第2层钢管数为5；即：25＝2+3‎ ‎ 第3层钢管数为6；即：36＝3+3‎ ‎ 第4层钢管数为7；即：47＝4+3‎ ‎ 第5层钢管数为8；即：58＝5+3‎ ‎ 第6层钢管数为9；即：69＝6+3‎ ‎ 第7层钢管数为10；即：710＝7+3‎ 若用表示钢管数，n表示层数，则可得出每一层的钢管数为一数列，且≤n≤7）‎ 运用每一层的钢筋数与其层数之间的对应规律建立了数列模型，运用这一关系，会很快捷地求出每一层的钢管数这会给我们的统计与计算带来很多方便。‎ 让同学们继续看此图片，是否还有其他规律可循？（启发学生寻找规律）‎ 模型二：上下层之间的关系 自上而下每一层的钢管数都比上一层钢管数多1。‎ 即；；‎ 依此类推：（2≤n≤7）‎ 对于上述所求关系，若知其第1项，即可求出其他项，看来，这一关系也较为重要。‎ 定义：‎ 递推公式：如果已知数列的第1项（或前几项），且任一项与它的前一项（或前n项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式 递推公式也是给出数列的一种方法。‎ 如下数字排列的一个数列：3，5，8，13，21，34，55，89‎ 递推公式为：‎ 数列可看作特殊的函数，其表示也应与函数的表示法有联系，首先请学生回忆函数的表示法：列表法，图象法，解析式法．相对于列表法表示一个函数，数列有这样的表示法：用 表示第一项，用 表示第一项，……，用 表示第 项，依次写出成为 ‎4、列表法 ‎．简记为 ．‎ ‎[范例讲解]‎ 例1 设数列满足写出这个数列的前五项。‎ 解：分析：题中已给出的第1项即，递推公式：‎ 解：据题意可知：，‎ ‎[补充例题]‎ 例2已知， 写出前5项，并猜想． ‎ 法一： ，观察可得 ‎ 法二：由 ∴ 即 ‎ ∴ ‎ ‎ 5．数列的前n项和：‎ 数列中，称为数列的前n项和，记为. ‎ 表示前1项之和：= ‎ ‎ 表示前2项之和：=‎ ‎……‎ 表示前n-1项之和：=‎ 表示前n项之和：=.‎ ‎∴当n≥1时才有意义；当n-1≥1即n≥2时才有意义.‎ ‎3．与之间的关系：‎ 由的定义可知，当n=1时，=；当n≥2时，=-，‎ 即=.‎ 说明：数列的前n项和公式也是给出数列的一种方法.‎ 三、例题讲解 例3已知数列的第1项是1，以后的各项由公式给出，写出这个数列的前5项 分析：题中已给出的第1项即，递推公式：‎ 解：据题意可知：‎ ‎ ‎ 例4已知数列中，≥3），试写出数列的前4项 解：由已知得 ‎ 例5已知， 写出前5项，并猜想． ‎ 法一： ，观察可得 ‎ 法二：由 ∴ 即 ‎ ∴ ‎ ‎ ∴ ‎ 例6 已知数列的前n项和，求数列的通项公式：‎ ‎⑴ =n+2n； ⑵ =n-2n-1.‎ 解：⑴①当n≥2时，=-=(n+2n)-[(n-1)+2(n-1)]=2n+1；‎ ‎②当n=1时，==1+2×1=3；‎ ‎③经检验，当n=1时，2n+1=2×1+1=3，‎ ‎∴=2n+1为所求.‎ ‎⑵①当n≥2时，=-=(n-2n-1)-[(n-1)+2(n-1)-1]=2n-3；‎ ‎②当n=1时，==1-2×1-1=-2；‎ ‎③经检验，当n=1时，2n-3=2×1-3=-1≠-2，‎ ‎∴=为所求.‎ Ⅲ.课堂练习 课本P36练习2‎ Ⅳ.课时小结 本节课学习了以下内容：‎ ‎1．递推公式及其用法；‎ ‎2．通项公式反映的是项与项数之间的关系，而递推公式反映的是相邻两项（或n项）之间的关系.‎ Ⅴ.课后作业 习题2。‎1A组的第4、6题 ‎§‎2.1.2‎数列的概念与简单表示法 课前预习 ‎1.数列的一个通项公式是 （ ）‎ A. B. C. D. ‎ ‎2.已知，则数列是 （ ） ‎ A. 递增数列 B. 递减数列 C. 常数列 D. 摆动数列 ‎3.数列的通项公式为，则数列各项中最小项是 （ ）‎ A. 第4项 B. 第5项 C. 第6项 D. 第7项 ‎4.已知数列的通项公式为，则3 （ ）‎ A. 不是数列中的项 B. 只是数列中的第2项 ‎ C. 只是数列中的第6项 D. 是数列中的第2项或第6项 ‎5.数列中，由给出的数之间的关系可知的值是（ ） ‎ A. 12 B. ‎15 C. 17 D. 18‎ ‎6.下列说法正确的是 （ ）‎ 数列1，3，5，7可表示为 ‎ 数列1，0，与数列是相同的数列 ‎ 数列的第项是 ‎ D. 数列可以看做是一个定义域为正整数集的函数 ‎7.数列的前n项和，则 。‎ ‎1.B2.A3.B4.D5.B6.C7‎ 课内探究 ‎1．根据各个数列的首项和递推公式，写出它的前五项，并归纳出通项公式 ‎(1) ＝0, ＝＋(2n－1) (n∈N)；‎ ‎(2) ＝1, ＝ (n∈N)；‎ ‎(3) ＝3, ＝3－2 (n∈N).‎ ‎ 解：(1) ＝0, ＝1, ＝4, ＝9, ＝16, ∴ ＝(n－1);‎ ‎(2) ＝1,＝,＝, ＝, ＝, ∴ ＝;‎ ‎(3) ＝3＝1+2, ＝7＝1+2, ＝19＝1+2, ‎ ‎＝55＝1+2, ＝163＝1+2, ∴ ＝1＋2·3;‎ ‎ 2． ．已知下列各数列的前n项和的公式，求的通项公式 ‎(1) ＝2n－3n; (2) ＝－2.‎ ‎ 解：(1) ＝－1, ‎ ‎=-＝2n－3n－[2(n－1)－3(n－1)]＝4n－5, ‎ 又符合＝4·1－5, ∴ ＝4n－5;‎ ‎(2) ＝1, =-＝－2－(－2)＝2·, ‎ ‎∴＝‎ ‎∴ ‎ 课后提高 ‎1. 设数列则是这个数列的 ‎ ‎ A.第六项 B.第七项 C.第八项 D.第九项 ‎2. 数列的前n项积为，那么当时，的通项公式为 ‎ ‎ A. B. C. D.‎ ‎3、若一数列的前四项依次是2，0，2，0，则下列式子中，不能作为它的通项公式的是（ ）。‎ ‎ （A）an= 1－(－1)n （B）an=1＋(－1)n＋1 ‎ ‎ （C）an=2sin2 （D）an=(1－cosnπ)＋(n－1)(n－2)‎ ‎4. 在数列中，，，则的值是 ‎ ‎ A. B. C. D.‎ ‎5. 数列的一个通项公式是 。‎ ‎6. 数列的前n项和，则 。‎ ‎7. 数列满足，则 。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎。‎ ‎8. 根据下列5个图形及相应点的个数的变化规律，猜测第个图中有___________个点.‎ ‎（1） （2） 　（3） 　　 （4） 　　　　　　　（5）‎ ‎9. 已知数列的前n项和，数列的前n项和，‎ ‎（1）若，求的值； （2）取数列中的第1项, 第3项, 第5项, 构成一个新数列, 求数列的通项公式.‎ ‎10.（1）已知数列的前n项和公式，求的通项公式　‎ ‎①；　　　　‎ ‎②‎ ‎ 1—4、BDDA 　　5、　　6、　　7、161　 8、8、　　‎ ‎9、（1）36　　（2）　　　　　10 (1) (2)‎ 等差数列教案 教学目标：‎ 知识与能力：理解等差数列的定义；掌握等差数列的通项公式；培养学生的观察、归纳能力，应用数学公式的能力及渗透函数、方程思想 ‎ 过程与方法：经历等差数列的产生过程和应用等差数列的基本知识解决问题的能力。‎ 情感态度与价值观：通过等差数列概念的归纳概括，培养学生的观察、分析能力，体验从特殊到一般认知规律，培养学生积极思维，追求新知的创新意识。‎ 教学重点：理解等差数列的概念，掌握等差数列的通项公式，体会等差数列与一次函数之间的联系。‎ 教学难点：概括通项公式推导过程中体现出的数学思想方法。‎ 教学准备：根据本节知识的特点，为突出重点、突破难点，增加教学容量，便于学生更好的理解和掌握所学的知识，我利用计算机辅助教学。‎ 教学过程：‎ 创设情境，课题导入 复习上节课学习的数列的定义及数列的表示法。这些方法从不同的角度反映了数列的特点，下面我们来看这样的一些数列：（大屏幕显示课本41页的四个例子）‎ ‎⑴、0 5 10 15 20 … …‎ ‎⑵、48 53 58 63‎ ‎⑶、18 15.5 13 10.5 8 5.5‎ ‎⑷、10072 10144 10216 10288 10360‎ 提出问题：以上四个数列有什么共同的特征？请同学们互相讨论。‎ ‎（二）设置问题，形成概念 ‎ 等差数列：一般地，如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列。这个常数就叫做等差数列的公差，常用字母d表示。‎ ‎ 提出问题：等差数列的概念中的几个关键点是什么？ ‎ ‎ 数学语言： 或 ≥1)‎ ‎ 理解等差数列的概念是本节课的重点，为了加深对概念的理解，让学生讨论课本45页练习第4题，教师总结。 ‎ ‎（三）等差数列的通项公式 ‎ 提出问题：如同我们在前一节看到的，能否确定一个数列的通项公式对研究这个数列具有重要的意义。数列⑴、⑵、⑶、⑷的通项公式存在吗？如果存在，分别是什么？‎ ‎ 再问：若一个无穷等差数列｛｝，首项是，公差为d，怎样得到等差数列的通项公式？（引导学生根据等差数列的定义进行归纳）‎ ‎ 即：‎ ‎ 即：‎ ‎ 即：‎ ‎ … …‎ ‎ 至此，让学生自己猜想通项公式是什么，使学生体会归纳、猜想在得出新结论中的作用。‎ ‎ 此处由归纳得出的公式只是一个猜想，严格的证明需要用数学归纳法的知识，在这里，我们暂且先承认它，我们能否再探索一下其他的推导方法？‎ ‎　（然后学生在教师的引导下一起探索另外的推导方法）‎ 叠加法：｛｝是等差数列，所以：‎ ‎ ‎ ‎ … …‎ ‎ ‎ ‎ 两边分别相加得： 所以：‎ 迭代法：｛｝是等差数列，则： ‎ ‎ = … …=‎ ‎ 所以：‎ ‎　　由以上关系还可得： 即：‎ ‎ 则：‎ ‎ =‎ 即得等差数列的第二通项公式：‎ ‎（四）通项公式的应用：‎ 观察通项公式并提出问题：要求等差数列的通项公式只需要求谁？‎ 再追问：通项公式中有几个未知量？‎ 再追问：要求其中的一个，需要知道其余的几个？‎ 例1、等差数列｛｝中，‎ ‎⑴已知： 求 ‎⑵已知： 求 ‎⑶已知： 求 ‎⑷已知： 求 ‎（题目比较简单，照顾到全体学生，使学生深刻掌握等差数列的通项公式，从而打好基础。）‎ 例2、1、求等差数列8、5、2… …的第20项 ‎ 解：由 得：‎ ‎ ‎ ‎ 2、是不是等差数列、、… …的项？如果是，是第几项？‎ ‎ 解：由 得 ‎ 由题意知，本题是要回答是否存在正整数n，使得：‎ ‎ 成立 ‎ 解得：即是这个数列的第100项。‎ 例3、某市出租车的计价标准为1.2元/km，起步价为10元，即最初的‎4km（不含‎4km）计费为10元，如果某人乘坐该市的出租车去往‎14km处的目的地，且一路畅通，等候时间为0，需要支付多少车费？‎ ‎ 分析：可以抽象为等差数列的数学模型。‎4km处的车费记为： 公差 当出租车行至目的地即‎14km处时，n=11 求 ‎ 所以：‎ 例4：数列是等差数列吗？‎ ‎（引导学生根据等差数列的定义求解，就是看 是不是一个与n无关的常数。）‎ ‎ 所以：｛｝是等差数列 引申：已知数列｛｝的通项公式，其中、为常数，这个数列是等差数列吗？若是，首项和公差分别是多少？‎ ‎　　（指定学生求解）‎ 解：取数列｛｝中任意两项和 ‎ ‎ ‎ ‎ 它是一个与n无关的常数，所以｛｝是等差数列？‎ ‎ 并且： ‎ 小结：上节课我们已学习过数列是一种特殊的函数，那么由此题启示，等差数列是哪一类函数？等差数列是关于正整数ｎ的一次函数，还可以是常数函数，当ｄ＝０的时候。‎ 通过例三，我们能否总结一下，到目前为至我们有哪些方法来判断一个数列是等差数列？‎ ‎　（学生讨论、回答，教师补充）‎ 一是利用定义： 或 ≥1)‎ 二是利用通项公式：　　是关于ｎ的一次函数或常数函数。‎ 课堂检测反馈：‎ 求等差数列10、８、６… 的第２０项。‎ ‎－20是不是等差数列０、3.5、－7… 的项？如果是，是第几项？如果不是，说明理由。‎ 等差数列｛｝中，已知： 求和 等差数列｛｝中，已知： 求 等差数列｛｝中，已知： 求、‎ ‎（五）课时小结：‎ ‎（学生自己归纳、补充，培养学生的口头表达能力和归纳概括能力，教师总结）‎ 等差数列的定义： 或 ≥1)‎ 等差数列的通项公式：或 ‎（六）课后作业：‎ ‎ 课本45页习题2．2（A组）3、4 ‎