江苏省南通市如东县2020-2021学年高三上学期期末考试数学试题 （word版含答案） 21页

2020~2021 学年度第一学期期末考试 高三数学 一､单项选择题:本题共 8 小题,每小题 5 分,共 40 分｡在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合 2{ ,0, 1}, { , ,0}A a B a b   ,若 A=B,则 2021( )ab 的值为() A.0 B.-1 C.1 D.±1 2.已知 a∈R,i 是虚数单位,若(1-i)(1+ai)=2,则 a=() A.1 . 5B C.3 . 6D 3.某大学 4 名大学生利用假期到 3 个山村参加基层扶贫工作,每名大学生只去 1 个山村,每个山村至少有 1 人 去,则不同的分配方案共有() A.6 种 B.24 种 C.36 种 D.72 种 4.胡夫金字塔的形状为四棱锥,1859 年,英国作家约翰｡泰勒(John Taylor, 1781-1846)在其《大金字塔》一书中提 出:古埃及人在建造胡夫金字塔时利用黄金比例 1 5( 1.618)2   ,泰勒还引用了古希腊历史学家希罗多德的记 载:胡夫金字塔的每一个侧面的面积都等于金字塔高的平方｡如图,若 2 ,h as 则由勾股定理, 2 2 ,as s a  即 2( ) 1 0,s s a a    因此可求得 s a 为黄金数,已知四棱锥底面是边长约为 856 英尺的正方形 (2 856),a  顶点 P 的 投影在底面中心 O，H 为 BC 中点,根据以上信息,PH 的长度(单位:英尺)约为() A.611.6 B.692.5 C.481.4 D.512.4 5.电影《我和我的家乡》于 2020 年 10 月 11 日在中国内地上映,到 2020 年 10 月 14 日已累计票房 22.33 亿, 创造了多个票房记录,某新闻机构想了解全国人民对《我和我的家乡》的评价,决定从某市 3 个区按人口数用 分层抽样的方法抽取一个样本｡若 3 个区人口数之比为 2:3:5,且人口最多的一个区抽出 100 人,则这个样本的 容量等于() A.100 B.160 C.200 D.240 6.若 1sin cos , (0, ),3       则 1 tan 1 tan     （） 17. 17A 17. 17B  15. 15C 15. 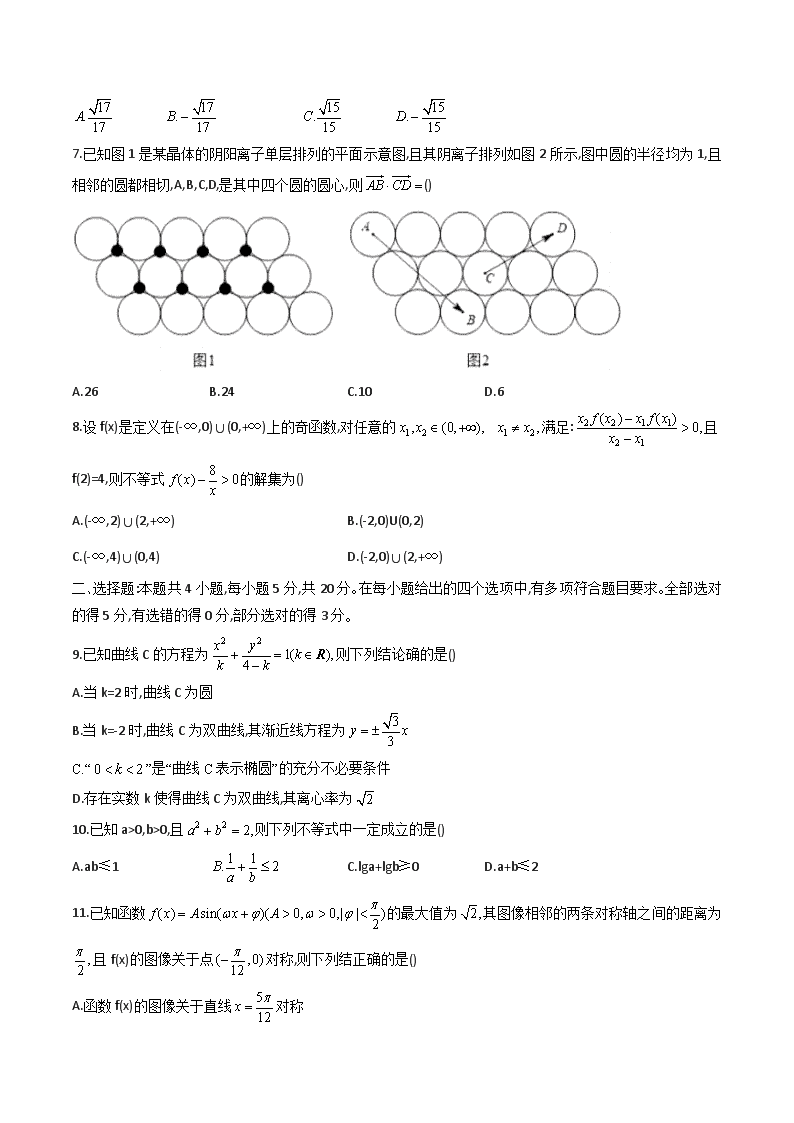15D  7.已知图 1 是某晶体的阴阳离子单层排列的平面示意图,且其阴离子排列如图 2 所示,图中圆的半径均为 1,且 相邻的圆都相切,A,B,C,D,是其中四个圆的圆心,则 AB CD   () A.26 B.24 C.10 D.6 8.设 f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,对任意的 1 2 1 2, (0, ), ,x x x x   满足: 2 2 1 1 2 1 ( ) ( ) 0,x f x x f x x x   且 f(2)=4,则不等式 8( ) 0f x x   的解集为() A.(-∞,2)∪(2,+∞) B.(-2,0)U(0,2) C.(-∞,4)∪(0,4) D.(-2,0)∪(2,+∞) 二､选择题:本题共 4 小题,每小题 5 分,共 20 分｡在每小题给出的四个选项中,有多项符合题目要求｡全部选对的 得 5 分,有选错的得 0 分,部分选对的得 3 分｡ 9.已知曲线 C 的方程为 2 2 1( ),4 x y kk k    R 则下列结论确的是() A.当 k=2 时,曲线 C 为圆 B.当 k=-2 时,曲线 C 为双曲线,其渐近线方程为 3 3y x  C.“ 0 2k  ”是“曲线 C 表示椭圆”的充分不必要条件 D.存在实数 k 使得曲线 C 为双曲线,其离心率为 2 10.已知 a>0,b>0,且 2 2 2,a b  则下列不等式中一定成立的是() A.ab≤1 1 1. 2B a b   C.lga+lgb≥0 D.a+b≤2 11.已知函数 ( ) sin( )( 0, 0,| | )2f x A x A         的最大值为 2,其图像相邻的两条对称轴之间的距离为 ,2  且 f(x)的图像关于点 ( ,0)12  对称,则下列结正确的是() A.函数 f(x)的图像关于直线 5 12x  对称 B.当 [ , ]6 6x    时,函数 f(x)的最小值为 2 2  C.若 3 2( ) ,6 5f    则 4 4sin cos  的值为 4 5y  D.要得到函数 f(x)的图像,只需要将 ( ) 2 cos2g x x 的图像向右平移 6  个单位 12.如图,在棱长为 1 的正方体 1 1 1 1ABCD A B C D 中,P 为线段 1 1B D 上一动点(包括端点),则以下结论正确的有() A.三棱锥 1P A BD 的体积为定值 1 3 B.过点 P 平行于平面 1A BD 的平面被正方体 1 1 1 1ABCD A B C D 截得的多边形的面积为 3 2 C.直线 1PA 与平面 1A BD 所成角的正弦值的范围为 3 6[ , ]3 3 D.当点 P 与 1B 重合时,三棱锥 1P A BD 的外接球的体积为 3 2  三､填空题:本大题共 4 小题,每小题 5 分,共 20 分｡不需写出解答过程,请把答案直接填写在答题卡相应位置上 ｡ 13.若双曲线 2 2 13 x y m   的右焦点与抛物线 2 12y x 的焦点重合,则 m=____. 14.朱载堉是中国明代一位杰出的音乐家､数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二 平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频 率之比完全相等,亦称"十二等程律”.即一个八度 13 个音,相邻两个音之间的频率之比相等,且最后一个音是最 初那个音的频率的 2 倍｡设第三个音的频率为 1,f 第七个音的频率为 2f ，则 2 1 f f  ____. 15. 设 向 量 1 1 2 2( , ), ( , ),a x y b x y   记 1 2 1 2 ,a b x x y y   若 圆 2 2: 4 8 0C x y x y    上 的 任 意 三 点 1 2 3 2 31 2, , ,A A A A A A A且 ,则 1 2 2 3| |OA OA OA OA      的最大值是____. 16.已知函数 2 1( 0) ( ) , 2 1( 0) x x x f x e x x x         则方程 2021( ) 2020f x  的实根的个数为____.函数 y=f(f(x)-a)-1 有三个零点, 则 a 的取值范围是_____. 四､解答题:本大题共 6 小题,共 70 分｡解答应写出文字说明､证明过程或演算步骤｡ 17.(本小题满分 10 分) 在   2 2 2, 1 cos cos cos sin sin2 B Casin A C bsin A B C B C     ① ② 两个条件中任选一个,补充到下面问题 中,并解答, 在△ABC 中,内角 A,B,C 的对边分别为 a,b,c,已知______. (1)求 A; (2)已知函数 1( ) cos(4 ), [0, ],2 4f x x A x    求 f(x)的最小值｡ 18.(本小题满分 12 分) 已知正项等比数列{ }na 的前 n 项和为 1 2 2 3, 2, 2nS a S a a   . (1)求数列{ }na 的通项公式; (2)设 2 1,n n nb a  求数列{ }nb 的前 n 项和 . 19.(本小题满分 12 分) 2020年国庆节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握国庆节期间车辆出 行的高峰情况,在某高速公路收费站点记录了 3日,上午9:20~10:40这一时间段内通过的车辆数,统计发现这一 时间段内共有 600 辆车通过该收费站点,它们通过该收费站点的时刻的频率分布直方图如下图所示,其中时间 段 9:20~9:40 记作[20,40)､9:40~10:00 记作[40,60),10:00~10:20 记作[ 60,80),10:20~10:40 记作[80,100),例如:10 点 04 分,记作时刻 64. (I)估计这 600 辆车在 9:20~10:40 时间内通过该收费站点的时刻的平均值(同一组中的数据用该组区间的中点 值代表); (I)为了对数据进行分析,现采用分层抽样的方法从这 600 辆车中抽取 10 辆,再从这 10 辆车随机抽取 4 辆,设抽 到的 4 辆车中,在 9:20~10:00 之 间通过的车辆数为 X,求 X 的分布列; (II)根据大数据分析,车辆在每天通过该收费站点的时刻 T 服从正态分布 2~ ( , ),T   其中μ可用 3 日数据中的 600 辆车在 9:20~10:40 之间通过该收费站点的时刻的平均值近似代替, 2 用样本的方差近似代替(同一组中 的数据用该组区间的中点值代表) .假如 4 日全天共有 1000 辆车通过该收费站点,估计在 9: 46~10:40 之间通过 的车辆数(结果保留到整数). 附:若随机变量 T 服从正态分布 2( , ),N   则 P(μ-σ