成人高考数学知识点梳理 10页

第一部分代数 第一章　集合和简易逻辑 一.元素与集合的关系： ‎ ‎ 或 ｘA 二.集合的运算：‎ ‎１.交集　　A∩B=｛ｘ︱且｝‎ ‎２.并集　　A∪B＝｛ｘ︱或｝‎ 三.充分条件.必要条件：‎ ‎１.充分条件：若，则是充分条件.‎ ‎２.必要条件：若，则是必要条件.‎ ‎３.充要条件：若，且，则是充要条件.‎ 注：如果甲是乙的充分条件，则乙是甲的必要条件；反之亦然.‎ 第二章 函数 一、 函数的定义：‎ ‎１.理解ｆ的含义，掌握求函数解析式的方法－配方法 ‎２.求函数值 ‎３.求函数定义域：１）分式的分母不等于０；２）偶次根式的被开方数≥０；３）对数的真数＞０；‎ 二.函数的性质 ‎１.单调性：（１）设那么 上是增函数；‎ 上是减函数.‎ ‎(2)设函数在某个区间内可导，如果，则为增函数；如果，则为减函数 ‎２.奇偶性　（１）定义：若，则函数是偶函数；若，则函数是奇函数.（２）奇偶函数的图象特征：奇函数的图象关于原点对称，偶函数的图象关于y轴对称;反过来，如果一个函数的图象关于原点对称，那么这个函数是奇函数；如果一个函数的图象关于y轴对称，那么这个函数是偶函数。（３）常见函数的图象及性质（熟记）‎ ‎３.反函数定义及求法：（１）反解；（２）互换ｘ，ｙ；（３）写出定义域。（文科不考）‎ ‎４.互为反函数的两个函数的关系：（文科不考）‎ ‎５.函数和与其反函数的图象关于直线y=x对称（文科不考）‎ ‎６.一次函数ｙ＝ｋｘ＋ｂ 图像是一条直线 ‎7.二次函数的解析式的三种形式：‎ ‎(1)一般式； ‎ ‎(2)顶点式；‎ ‎(3)两根式 ‎８.二次函数的最值： 二次函数在闭区间上的最值只能在处及区间的两端点处取得，具体如下：‎ ‎(1)当a>0时，若，则；‎ 若，，.‎ ‎(2)当a<0时，若，则；‎ 若，则，‎ 分数指数幂 ‎ ‎(1)（，且）；(2)（，且）.‎ ‎９. 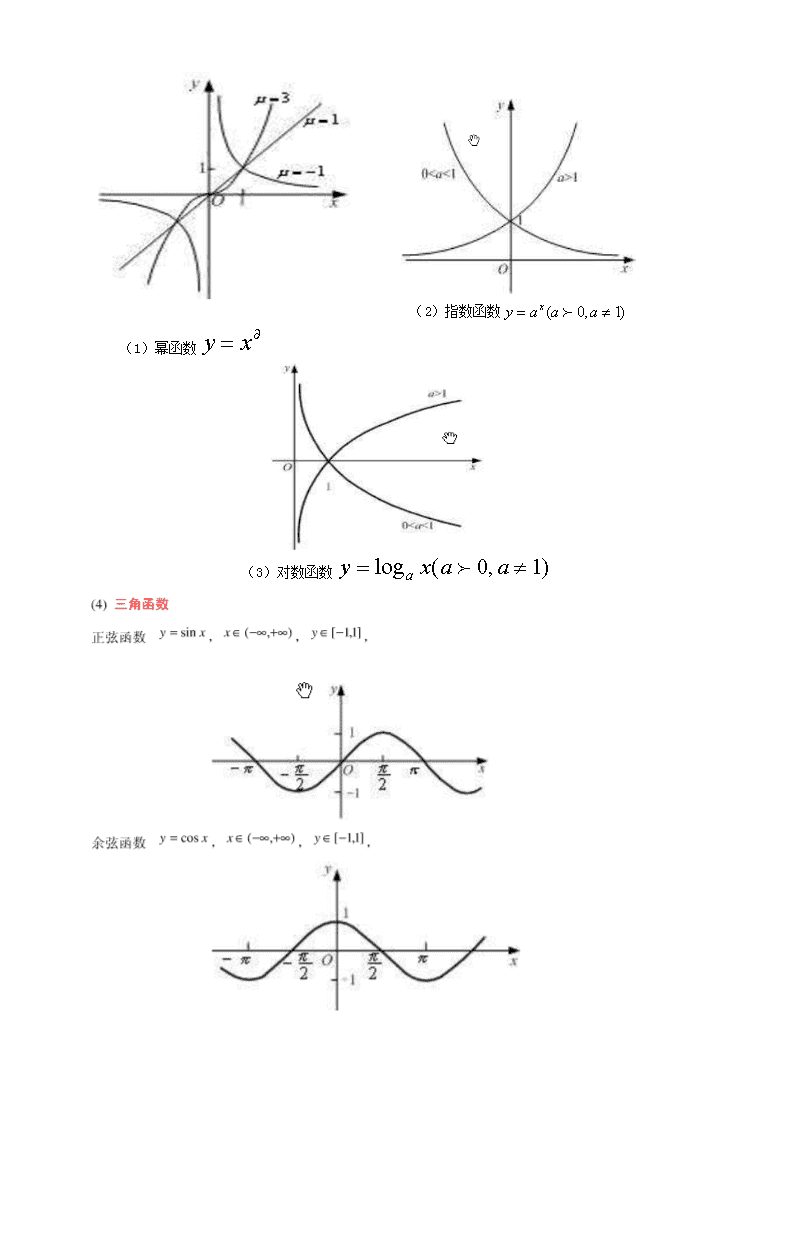二次函数图像、性质 ‎10.根式的性质 ‎（1）.（2）当为奇数时，； 当为偶数时，.‎ ‎11.有理指数幂的运算性质 ‎(1)；(2)；(3)‎ ‎12.指数式与对数式的互化式★‎ ‎ .‎ ‎13.对数的换底公式 ‎ ‎ (,且,,且, ).‎ 推论 (,且,,且,, ).‎ ‎14.对数的四则运算法则 若a＞0，a≠1，M＞0，N＞0，则 ‎(1) ;‎ ‎(2) ;(3).‎ ‎15.常见函数的图像 ‎ ‎ （2）指数函数 ‎（1）幂函数 ‎ ‎（3）对数函数 第三章　不等式与不等式组 ‎１.含绝对值的不等式　‎ 当a>0时，有；或 ‎２.一元二次不等式，如果与同号，则其解集在两根之外；如果与异号，则其解集在两根之间.简言之：同号两根之外，异号两根之间.‎ ‎；‎ 第四章　数列 ‎１.数列的通项公式与前n项的和的关系 . ★‎ ‎２.等差数列：‎ ‎３.等差数列的通项公式：；‎ 其前n项和公式为：.‎ ‎４.等比数列：‎ ‎５.等比数列的通项公式：；★‎ 其前n项的和公式为：或.‎ 第五章　复数（文科不考）‎ ‎１.复数的相等：.（）‎ ‎２.复数的模（或绝对值）：==.实部：；虚部：ｂ ‎３.复数的四则运算法则（ｉ２＝－１）★‎ ‎(1);(2);‎ ‎(3);‎ ‎(4)‎ ‎４.实系数一元二次方程的解：实系数一元二次方程，①若,则;②若,则;③若，它在实数集内没有实数根；在复数集内有且仅有两个共轭复数根 ‎５.★一元二次方程根与系数的关系：‎ 第六章　导数★★★★★‎ ‎１.导数的计算　‎ ‎（１）公式　‎ ‎（为常数）　（） （文科不考）（文科不考）　　（文科不考）‎ ‎（２）求导数的四则运算法则：（其中必须是可导函数.）‎ ‎（为常数）（文科不考）　　　（文科不考）‎ ‎２.导数的应用　　‎ ‎（１）利用几何意义求曲线的切线方程：函数在点处的导数的几何意义就是曲线在点处的切线的斜率，也就是说，曲线在点P处的切线的斜率是，切线方程为 ‎（２）判断函数单调性.求极值.求最值： ‎ ‎１０.函数单调性的判定方法：设函数在某个区间内可导，如果＞0，则为增函数；如果＜0，则为减函数 ‎２０.极值的判别方法：（极值是在附近所有的点，都有＜，则是函数的极大值，极小值同理）当函数在点处连续时，‎ ①如果在附近的左侧＞0，右侧＜0，那么是极大值；‎ ②如果在附近的左侧＜0，右侧＞0，那么是极小值.‎ 也就是说是极值点的充分条件是点两侧导数异号，而不是=0①. 此外，函数不可导的点也可能是函数的极值点②. 当然，极值是一个局部概念，极值点的大小关系是不确定的，即有可能极大值比极小值小（函数在某一点附近的点不同）.‎ 注①： 若点是可导函数的极值点，则=0. 但反过来不一定成立. 对于可导函数，其一点是极值点的必要条件是若函数在该点可导，则导数值为零. 例如：函数，使=0，但不是极值点.‎ ②例如：函数，在点处不可导，但点是函数的极小值点.‎ ‎３.极值与最值的区别：极值是在局部对函数值进行比较，最值是在整体区间上对函数值进行比较.‎ 注：函数的极值点一定要有意义.‎ 第二部分　三角 ‎１.三角函数在四个象限内的符号：函.弦.切.余 ‎２.★同角三角函数的基本关系式：， =， .‎ ‎ 1‎ ‎ ‎ ‎ ‎ ‎２.正弦.余弦的诱导公式：奇变偶不变，符号看象限。‎ ‎， ‎ ‎３.★和角与差角公式 ‎;‎ ‎;‎ ‎.‎ ‎４.二倍角：‎ ‎；‎ ‎；‎ ‎.‎ ‎５.★三角函数的周期公式 ：‎ 函数及函数的周期；‎ 函数的周期.‎ ‎６.★正弦定理：‎ ‎（为的外接圆半径）.‎ ‎７．★余弦定理：‎ ‎；；‎ ‎８.三角形内角和定理 ‎ 在△ABC中，有 ‎9.三角形面积公式：‎ ‎10.特殊角三角函数值 三角函数 α ‎30°‎ ‎45°‎ ‎60°‎ 三角函数值的前三行，分子被开方数排列特征依次为“1，2，3，3，2，1，3，9，27”。‎ ‎“一二三，三二一，三九二十七”。记此歌诀即可。‎ 角度 函数 ‎0‎ ‎90‎ ‎180‎ ‎270‎ ‎360‎ 角a的弧度 ‎0‎ π/2‎ π ‎3π/2‎ ‎2π sin ‎0‎ ‎1‎ ‎0‎ ‎-1‎ ‎0‎ cos ‎1‎ ‎0‎ ‎-1‎ ‎0‎ ‎1‎ tan ‎0‎ 不存在 ‎0‎ 不存在 ‎0‎ Cot 不存在 ‎0‎ 不存在 ‎0‎ 不存在 记忆歌诀：0,1,0，负，0；1,0，负，0,1；0，不，0，不，0；不，0，不，0，不。‎ 第三部分 平面解析几何 ‎１.★平面向量基本定理：如果e1.e 2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数λ1.λ2，使得a=λ1e1+λ2e2．不共线的向量e1.e2叫做表示这一平面内所有向量的一组基底．‎ ‎２.★向量平行的坐标表示： 设a=,b=，则a∥b.‎ ‎３.★ a与b的数量积(或内积)　　a·b=|a||b|cosθ．（文科不考）‎ ‎４. a·b的几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积．（文科不考）‎ ‎５.★平面向量的坐标运算 ‎(1)设a=,b=，则a+b=.‎ ‎(2)设a=,b=，则a-b=. ‎ ‎ (3)设A，B,则.‎ ‎(4)设a=，则a=.‎ ‎(5)设a=,b=，则a·b=.‎ ‎６.两向量的夹角公式 ‎(a=,b=).‎ ‎７.平面两点间的距离公式 ‎ = (其中A，B).‎ ‎８.线段的中点公式  ‎ 设，，是线段的中点，则　　.‎ ‎８.向量的平行与垂直 ★‎ 设a=,b=，则a∥bb=λa ；‎ aba·b=0.‎ ‎９.斜率公式：（.）.‎ ‎10.直线的五种方程 ‎ ‎★（1）点斜式 (直线过点，且斜率为)．‎ ‎（2）斜截式 (b为直线在y轴上的截距).‎ ‎（3）两点式 ()(. ()).‎ ‎(4) 截距式 (分别为直线的横.纵截距，)‎ ‎（5）一般式 (其中A.B不同时为0).‎ ‎11.★两条直线的平行和垂直 ‎ ‎(1)若，‎ ‎①；②.‎ ‎(2)若,,且A2.B2 .C2都不为零,‎ ‎①；②；‎ ‎12.夹角公式：.(，,)‎ ‎13.★点到直线的距离：(点，直线：).‎ ‎14.★点在曲线上，则点的坐标满足曲线的方程。‎ ‎15.★求曲线与曲线的交点，将曲线方程联立方程组求解，以方程的解为坐标即为交点坐标。‎ ‎16.★圆的三种方程 ‎（1）圆的标准方程 .‎ ‎（2）圆的一般方程 (＞0).‎ ‎（3）圆的参数方程 ‎ ‎17.直线与圆的位置关系：‎ 直线与圆的位置关系有三种:；；.‎ 其中.‎ ‎18.★椭圆的方程 ‎（１）标准方程（焦点在ｘ轴）‎ ‎（焦点在ｙ轴）‎ ‎（２）参数方程是　　‎ ‎19.★椭圆的长轴长：，短轴长；２ｂ；焦距：２ｃ；离心率： ‎ 其中：ｃ２＝－ｂ２，注意：分母大的为 ‎20.★双曲线的方程：（焦点在ｘ轴）‎ ‎（焦点在ｙ轴）‎ ‎21.★双曲线的实轴长：，虚轴长；２ｂ；焦距：２ｃ；离心率： ‎ 其中：ｃ２＝＋ｂ２，注意：被减量的分母为 ‎22.★双曲线的方程与渐近线方程的关系：‎ ‎(1）若双曲线方程为渐近线方程：‎ ‎(２）若双曲线方程为渐近线方程：‎ ‎23.★抛物线的标准方程…………焦点坐标…………准线方程…………开口方向 ‎（１）…………F()……………………　向右 ‎（２）…………F()……………………向左 ‎（３）…………F()……………………　向上 ‎（４）…………F()……………………　向下 其中：P表示定点（焦点）到定直线（准线）的距离 第四部分　立体几何（文科不考）‎ ‎１.体.锥体的体积 ‎（是柱体的底面积.是柱体的高）‎ ‎（是锥体的底面积.是锥体的高）‎ ‎２.★球的半径是R，则其体积,其表面积．‎ ‎３.异面直线的定义及异面直线所成的角 第五部分　概率与统计 ‎１.★分类加法原理（加法原理）‎ ‎.‎ ‎２.★分步计数原理（乘法原理）‎ ‎.　　　　　总结：分类之间算加法；分步之间算乘法。‎ ‎３.排列数公式 ‎ ‎==.(，∈N*，且)．注:规定.‎ ‎４.二项式定理 ;‎ 二项展开式的通项公式.‎ ‎５★.等可能性事件的概率 ‎（其中：ｍ表示一次试验共有ｎ种等可能出现的结果，其中试验A包含的结果有ｍ种）‎ ‎６.互斥事件A，B分别发生的概率的和P(A＋B)=P(A)＋P(B)．‎ ‎７.个互斥事件分别发生的概率的和P(A1＋A2＋…＋An)=P(A1)＋P(A2)＋…＋P(An)．‎ ‎８.独立事件A，B同时发生的概率P(A·B)= P(A)·P(B).‎ ‎９.n个独立事件同时发生的概率 P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An)．‎ ‎10.n次独立重复试验中某事件恰好发生k次的概率 ‎11.离散型随机变量的分布列的两个性质：（1）；（2）.‎ ‎12★.随机变量的分布列是 ｘ１‎ ｘ２‎ ｘ３‎ ｘ４‎ ‎……‎ ｘｎ ｐ P1‎ P２‎ P３‎ P４‎ ‎……‎ Pｎ 数学期望 ‎13★.设样本数据为，则样本平均数，‎ 样本方差：‎ 注意：计算样本平均数与样本方差可以使用计算器。‎