高中数学必修3教案：5_示范教案（1_2_3循环语句） 8页

‎1.2.3循环语句 整体设计 教学分析 ‎ 通过前面的学习，学生学会了输入语句、输出语句、赋值语句和条件语句的基本用法，本节将介绍循环语句的用法. 程序中的循环语句与程序框图中的循环结构存在一一对应关系，这种对应关系对于学生理解循环语句的结构，进一步理解算法中的循环结构都是很有帮助的.我们可以给出循环语句的一般格式，让学生自己画出相应的程序框图，也可以给出程序框图，让学生写出算法语句，提高学生的应用能力.‎ 三维目标 ‎1．理解学习基本算法语句的意义.‎ ‎2．学会循环语句的基本用法.‎ ‎3.理解算法步骤、程序框图和算法语句的关系，学会算法语句的写法.‎ 重点难点 教学重点：循环语句的基本用法.‎ 教学难点：循环语句的写法.‎ 课时安排1课时 教学过程 导入新课 ‎ 思路1（情境导入）‎ ‎ 一位同学不小心违反了学校纪律，班主任令其写检查，他写完后交给班主任，班主任看后说：“认识不深刻，拿回去重写，直到认识深刻为止”.这位同学一想，这不是一个循环结构吗？可惜我还没学循环语句，不然可以写一个算法语句输入计算机了.同学们，今天我们开始学习循环语句.‎ ‎ 思路2（直接导入）‎ ‎ 前面我们学习了程序框图的画法,为了让计算机能够理解算法步骤、程序框图，上一节我们学习了输入语句、输出语句、赋值语句和条件语句，今天我们开始学习循环语句.‎ 推进新课 新知探究 提出问题 ‎（1）试用程序框图表示循环结构.‎ ‎（2）指出循环语句的格式及功能.‎ ‎（3）指出两种循环语句的相同点与不同点.‎ ‎（4）揭示程序中的循环语句与程序框图中的条件结构存在一一对应关系.‎ 讨论结果：‎ ‎（1）循环结构 ‎ 循环结构有两种形式：当型循环结构和直到型循环结构.‎ ‎ 1°当型循环结构，如图（1）所示 ‎ 2°直到型循环结构，如图（2）所示，‎ ‎ ‎ ‎（1）当型循环结构 （2）直到型循环结构 ‎（2）循环语句 ‎ 1°当型循环语句 ‎ 当型（WHILE型）语句的一般格式为：‎ ‎ WHILE 条件 ‎ 循环体 ‎ WEND ‎ 功能：计算机执行此程序时，遇到WHILE语句，先判断条件是否成立，如果成立，则执行WHILE和WEND之间的循环体；然后返回到WHILE语句再判断上述条件是否成立，如果成立，再执行循环体，这个过程反复执行，直到一次返回到WHILE语句判断上述条件不成立为止，这时不再执行循环体，而是跳到WEND语句后，执行WEND后面的语句.因此当型循环又称“前测试型”循环，也就是我们经常讲的“先测试后执行”“先判断后循环”.‎ ‎2°直到型循环语句 ‎ 直到型（UNTIL型）语句的一般格式为：‎ ‎ DO ‎ 循环体 ‎ LOOP UNTIL 条件 功能：计算机执行UNTIL语句时，先执行DO和LOOP UNTIL之间的循环体，然后判断“LOOP UNTIL”后面的条件是否成立，如果条件不成立，返回DO语句处重新执行循环体.这个过程反复执行，直到一次判断“LOOP UNTIL”后面的条件成立为止，这时不再返回执行循环体，而是跳出循环体执行“LOOP UNTIL条件”下面的语句.‎ ‎ 因此直到型循环又称“后测试型”循环，也就是我们经常讲的“先执行后测试”“先循环后判断”.‎ ‎(3)相同点：都是反复执行循环体语句.‎ 不同点：当型循环语句是先判断后循环，直到型循环语句是先循环后判断.‎ ‎(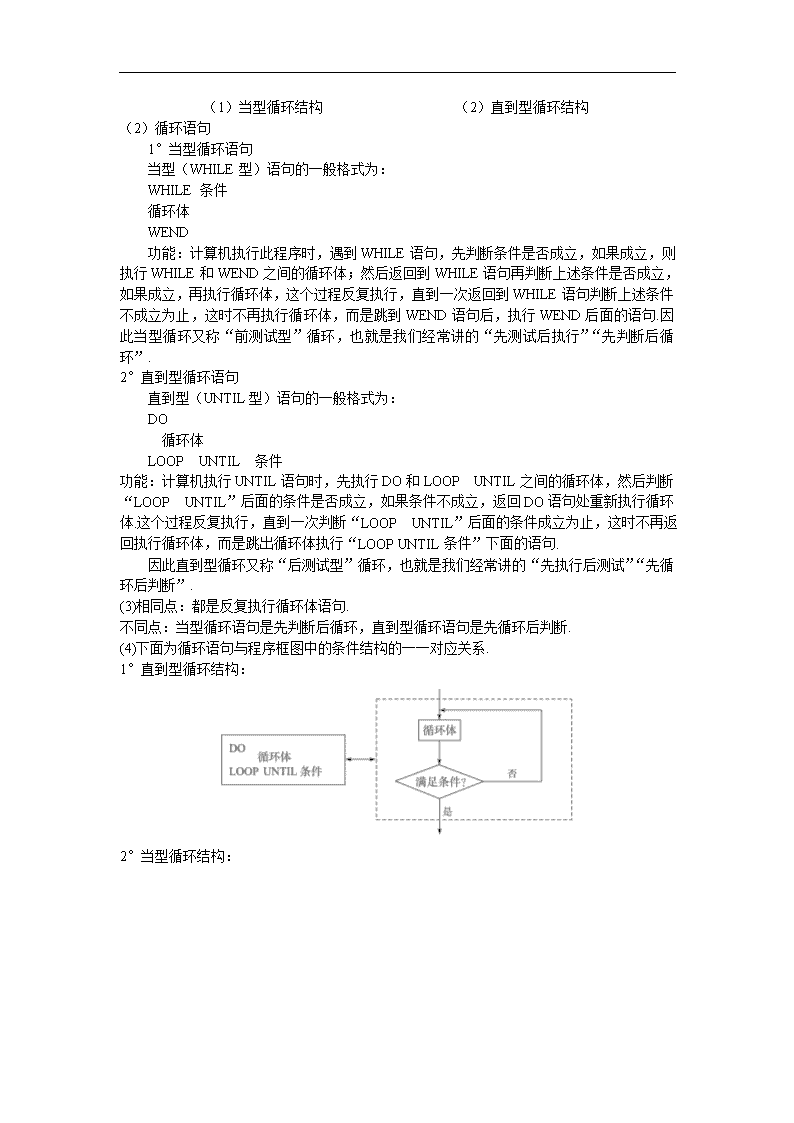4)下面为循环语句与程序框图中的条件结构的一一对应关系.‎ ‎1°直到型循环结构：‎ ‎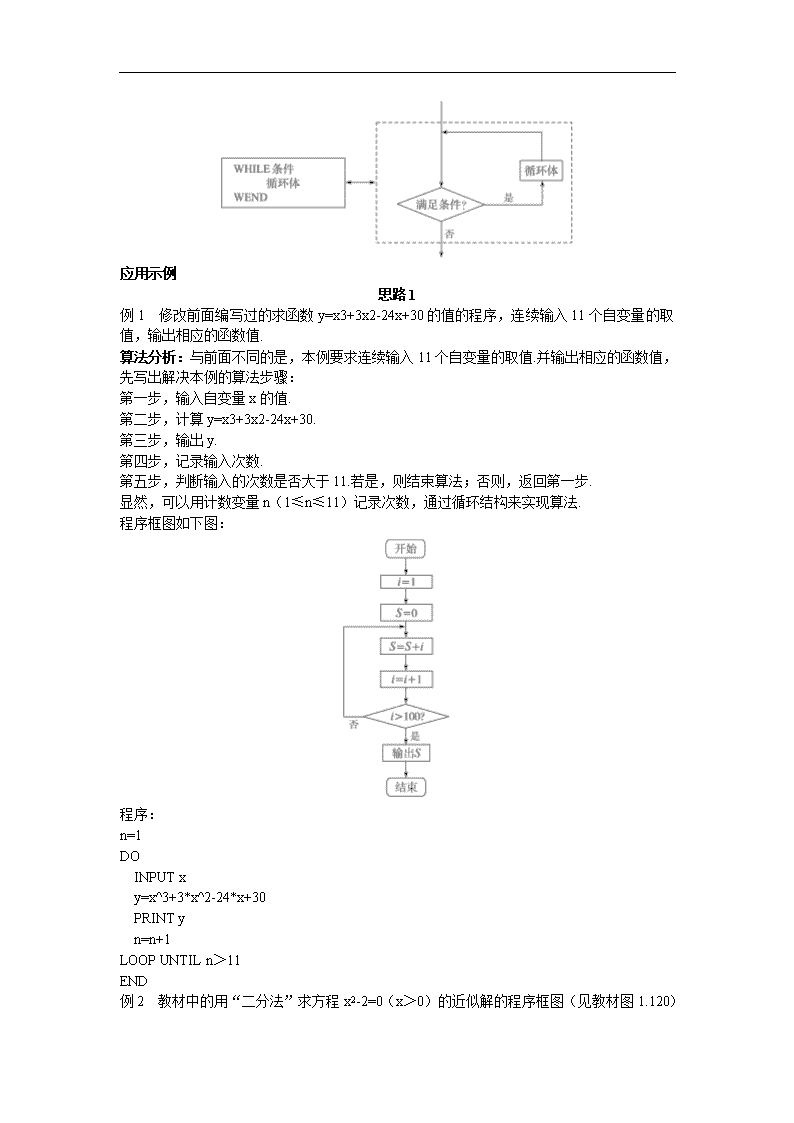2°当型循环结构：‎ 应用示例 思路1‎ 例1 修改前面编写过的求函数y=x3+3x2-24x+30的值的程序，连续输入11个自变量的取值，输出相应的函数值.‎ 算法分析：与前面不同的是，本例要求连续输入11个自变量的取值.并输出相应的函数值，先写出解决本例的算法步骤：‎ 第一步，输入自变量x的值.‎ 第二步，计算y=x3+3x2-24x+30.‎ 第三步，输出y.‎ 第四步，记录输入次数.‎ 第五步，判断输入的次数是否大于11.若是，则结束算法；否则，返回第一步.‎ 显然，可以用计数变量n（1≤n≤11）记录次数，通过循环结构来实现算法.‎ 程序框图如下图：‎ 程序：‎ n=1‎ DO ‎ INPUT x ‎ y=x^3+3*x^2-24*x+30‎ ‎ PRINT y ‎ n=n+1‎ LOOP UNTIL n＞11‎ END 例2 教材中的用“二分法”求方程x2-2=0（x＞0）的近似解的程序框图（见教材图1.120‎ ‎）包含了顺序结构、条件结构和循环结构.下面，我们把这个程序框图转化为相应的程序.‎ 解：程序为：‎ INPUT “a,b,d=”；a,b,d DO ‎ m=(a+b)/2‎ ‎ g=a^2-2‎ ‎ f=m^2-2‎ ‎ IF g*f＜0 THEN ‎ b=m ‎ ELSE ‎ a=m ‎ END IF LOOP UNTIL ABS(a-b)＜d OR f=0‎ PRINT m END 点评：ABS（）是一个函数，用来求某个数的绝对值，即ABS（x）=|x|.‎ 例3 设计一个计算1×3×5×7×…×99的算法，编写算法程序.‎ 解：算法如下：‎ 第一步，s＝1.‎ 第二步，i＝3.‎ 第三步，s＝s×i.‎ 第四步，i＝i＋2.‎ 第五步，如果i≤99，那么转到第三步.‎ 第六步，输出s.‎ 程序如下：（“WHILE型”循环语句）‎ s＝1‎ i＝3‎ WHILE i＜＝99‎ ‎ s＝s*i ‎ i＝i＋2‎ WEND PRINT s END 点评：前面我们已经学过“求和”问题，这是一个“求积”问题，这两个问题都是典型的算法问题，注意它们的联系与区别.‎ 例4 编写一个程序，求1!+2!+…+10!的值（其中n！=1×2×3×…×n）.‎ 分析：这个问题可以用“WHILE+ WHILE”循环嵌套语句格式来实现.‎ 程序结构要做到如下步骤：‎ ‎①处理“n！”的值；（注：处理n！的值的变量是一个内循环变量）‎ ‎②累加“n！”的值.（注：累加n！的值的变量是一个外循环变量）‎ 显然，通过10次循环可分别求出1!、2!、…、10!的值，并同时累加起来, 可求得S的值.而求T=n！，又可以用一个循环（内循环）来实现.‎ 解：程序为：‎ s=0‎ i=1‎ WHILE i<=10‎ ‎ j=1‎ ‎ t=1‎ ‎ WHILE j<=i ‎ t=t*j ‎ j=j+1‎ WEND ‎ s=s+t ‎ i=i+1‎ WEND PRINT s END 思考：上面程序中哪个变量是内循环变量，哪个变量是外循环变量？‎ 解答：内循环变量：j，t.外循环变量：s，i.‎ ‎ 上面的程序是一个的“WHILE+WHILE”型循环嵌套语句格式.这是一个比较好想的方法，但实际上对于求n！，我们也可以根据求出的(n－1)!乘上n即可得到，而无需重新从1再累乘到n.‎ 程序可改为：‎ s=0‎ i=1‎ j=1‎ WHILE i<=10‎ ‎ j=j*i ‎ s=s+j ‎ i=i+1‎ WEND PRINT s END ‎ 显然第二个程序的效率要比第一个高得多.第一程序要进行1+2+…+10=55次循环，而第二程序进行10次循环.如题目中求的是1！＋2！＋…＋1 000！，则两个程序的效率区别会更明显.‎ 点评：解决具体的构造循环语句的算法问题，要尽可能地少引入循环变量，否则较多的变量会使得设计程序比较麻烦，并且较多的变量会使得计算机占用大量的系统资源，致使系统缓慢.另外，也尽可能使得循环嵌套的层数少，否则也浪费计算机的系统资源.‎ 变式训练 ‎ 某种蛋白质是由四种氨基酸组合而成.这四种氨基酸的相对分子质量分别是57，71，97，101.实验测定蛋白质的相对分子质量为800.问这种蛋白质的组成有几种可能？‎ 分析：该问题即求如下不定方程的整数解：设四种氨基酸在蛋白质的组成中分别各有x，y，z，w个.则由题意可得57x+71y+97z+101w=800，（x，y，z，w是非负整数）‎ ‎ 这里0≤x≤14，0≤y≤11，0≤z≤8，0≤w≤7，利用穷取法，考虑一切可能出现的情况.运用多层循环嵌套处理即可.‎ 解：编写程序如下：‎ w=0‎ WHILE w<=7‎ ‎ z=0‎ WHILE z<=8‎ ‎ y=0‎ WHILE y<=11‎ ‎ x=0‎ WHILE x<=14‎ ‎ IF 57*x+71*y+97*z+101*w=800 THEN ‎ PRINT x，y，z，w ‎ END IF ‎ x=x+1‎ WEND ‎ y=y+1‎ WEND ‎ z=z+1‎ WEND ‎ w=w+1‎ WEND END 知能训练 设计算法求的值.要求画出程序框图，写出用基本语句编写的程序.‎ 解：这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示：‎ 程序如下：‎ s=0‎ i=1‎ Do s=s+1/（i*(i+1)）‎ i=i+1‎ LOOP UNTIL i>99‎ PRINT s END 拓展提升 ‎ 青年歌手电视大赛共有10名选手参加，并请了12名评委，在计算每位选手的平均分数时，为了避免个别评委所给的极端分数的影响，必须去掉一个最高分和一个最低分后再求平均分.试设计一个算法解决该问题，要求画出程序框图，写出程序（假定分数采用10分制，即每位选手的分数最高分为10分，最低分为0分）.‎ 解：由于共有12位评委，所以每位选手会有12个分数，我们可以用循环语句来完成这12个分数的输入，同时设计累加变量求出这12个分数的和，本问题的关键在于从这12个输入分数中找出最大数与最小数，以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间，我们可以先假设其中的最大数为0，最小数为10，然后每次输入一个评委的分数，就进行一次比较，若输入的数大于0,就将之代替最大数，若输入的数小于10，就用它代替最小数，依次下去，就能找出这12个数中的最大数与最小数，循环结束后，从总和中减去最大数与最小数，再除以10，就得到该选手最后的平均分.‎ 程序框图如右图：‎ 程序如下：s=0‎ i=1‎ max=0‎ min=10‎ DO INPUT x s=s+x IF max<=x THEN max=x END IF IF min>=x THEN min=x END IF i=i+1‎ LOOP UNTIL i>12‎ s1=s－max－min a=s1/10‎ PRINT a END 课堂小结 ‎（1）学会两种循环语句的应用.‎ ‎(2)熟练应用两种循环语句编写计算机程序，巩固算法应用.‎ 作业 ‎ 习题1.2A组3.‎ 设计感想 ‎ 本节的导入符合学生心理要求，能够激发学生的学习兴趣.算法像一个故事，循环语句就是故事的高潮，它以前面的内容为基础，是前面内容的总结和发展.本节选用了大量的精彩例题为故事高潮的到来作好了铺垫，精彩的点评把本节推向了高潮，所以本节教案值得期待.‎