2020年天津市滨海新区高考数学模拟试卷(5月份) (含答案解析) 16页

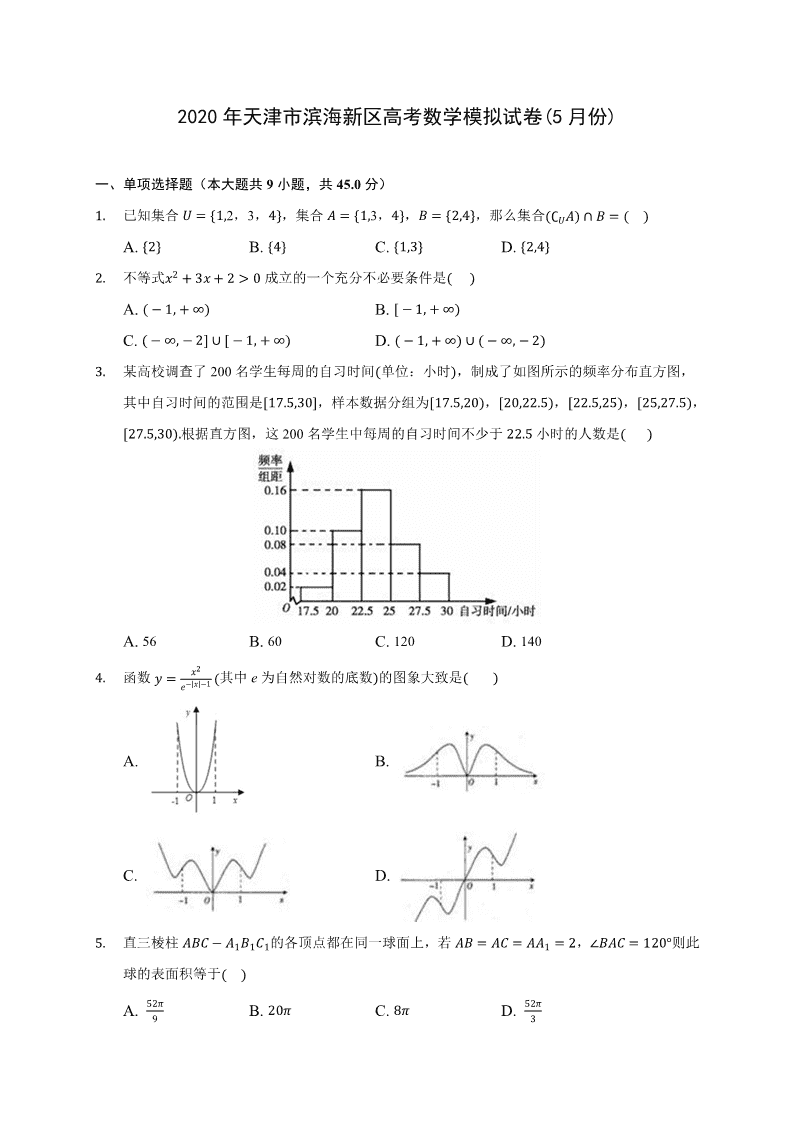
2020 年天津市滨海新区高考数学模拟试卷(5 月份) 一、单项选择题（本大题共 9 小题，共 45.0 分） 1. 已知集合 ൌ 1 2，3， ，集合 ൌ 1 3， ， ൌ ሼ ，那么集合 ൌ A. ሼ B. C. 1ǡ D. ሼ ሼ. 不等式 ሼ ǡ ሼ ൅ 成立的一个充分不必要条件是 A. െ 1 B. െ 1 C. െ െ ሼ െ 1 D. െ 1 െ െ ሼ ǡ. 某高校调查了 200 名学生每周的自习时间 单位：小时 ，制成了如图所示的频率分布直方图， 其中自习时间的范围是 1.ǡ ，样本数据分组为 1.ሼ ， ሼሼሼ. ， ሼሼ.ሼ ， ሼሼ. ， ሼ.ǡ. 根据直方图，这 200 名学生中每周的自习时间不少于 ሼሼ. 小时的人数是 A. 56 B. 60 C. 120 D. 140 . 函数 ൌ ሼ െ െ1 其中 e 为自然对数的底数 的图象大致是 A. B. C. D. . 直三棱柱 棱 െ 11棱1 的各顶点都在同一球面上，若 ൌ 棱 ൌ 1 ൌ ሼ ， 棱 ൌ 1ሼ 则此 球的表面积等于 A. ሼ B. ሼ C. D. ሼ ǡ 6. 已知函数 ൌെ ，则 是 A. 奇函数 B. 偶函数 C. 既是奇函数又是偶函数 D. 非奇函数非偶函数 . 已知函数 ൌ sin ，其中 ൅ ， ，若 图象上相邻两条对称轴之间的 距离为 ，且当 时， 取得最大值，则 在 上 A. 是减函数 B. 是增函数 C. 先增后减函数 D. 先减后增函数 . 已知双曲线 ሼ െ ሼ ൌ 1 与抛物线 ሼ ൌ 的一个交点为 P，F 为抛物线的交点，若 晦䁪 ൌ ，则 双曲线的离心率为 A. ሼ B. 4 C. ǡ D. 2 . 已知函数 ，若函数 ൌ 1 有三个零点，则实数 m 的 取值范围是 A. ሼ B. ሼǡ C. ሼǡ D. 1ǡ二、填空题（本大题共 6 小题，共 30.0 分） 1. 复数 െሼ ൌ ______ ． 11. ሼ ሼ 的展开式中 的系数为________． 1ሼ. 圆心在直线 ሼ െ െ ǡ ൌ 上，且过点 ሼ ， ǡ െ ሼ 的圆的标准方程为___________ 1ǡ. 已知袋子中有大小相同的红球 1 个，黑球 2 个，从中任取 2 个．设 表示取到红球的个数，则 ൌ ______， ൌ ______． 1. 已知实数 ൅ ， ൅ ，且 1 ൌ ሼ ，则 xy 的最小值为______． 1. 在平面四边形 ABCD 中，点 E，F 分别是边 AD，BC 的中点，且 ൌ 1 ， 䁪 ൌ ሼ ， 棱 ൌ ， 则 棱 的值为______ ． 三、解答题（本大题共 5 小题，共 75.0 分） 16. 在 棱 中，内角 A，B，C 所对的边为 a，b，c，且满足 െ棱 ൌ െ h ． Ⅰ 求 C； Ⅱ 若 h݋ ൌ 1 ，求 cosሼ െ 棱 的值． 1. 如图，在四棱锥 晦 െ 棱 中，底面 ABCD 为平行四边形， ൌ ， 晦 平面 ABCD， 晦 ． 1 证明： 棱 平面 PDB； ሼ 若 ൌ ሼ晦 与平面 APD 所成角为 ，求二面角 െ 晦棱 െ 的大小． 1. 设 是公比不为 1 的等比数列， 1 为 ሼ 、 ǡ 的等差中项． 1 求 的公比； ሼ 若 1 ൌ 1 ，求数列 的前 n 项和． 1. 已知椭圆 棱 ： ሼ ሼ ሼ ሼ ൌ 1 ൅ ൅ 的上、下顶点分别为 A，B，且 ൌ ሼ ，离心率为 ǡ ሼ ，O 为 坐标原点． Ⅰ 求椭圆 C 的方程； Ⅱ 设 P，Q 是椭圆 C 上的两个动点 不与 A，B 重合 ，且关于 y 轴对称，M，N 分别是 OP， BP 的中点，直线 AM 与椭圆 C 的另一个交点为 . 求证：D，N，Q 三点共线． ሼ. 已知函数 ൌ ሼ െ 1 െ ，其中 ． 1 讨论 的单调性； ሼ 若 对 1 成立，求实数 a 的取值范围． 【答案与解析】 1.答案：A 解析：解：集合 ൌ 1 2，3， ，集合 ൌ 1 3， ， ൌ ሼ ， ൌ ሼ ， ൌ ሼ ． 故选：A． 根据补集与交集的定义，进行运算即可． 本题考查了交集与补集的定义与运算问题，是基础题目． 2.答案：A 解析： 本题考查了充分必要条件，考查不等式问题，是一道基础题． 解不等式，根据集合的包含关系求出答案即可． 解： ሼ ǡ ሼ ൅ ， 1 ሼ ൅ ， 解得： ൅െ 1 或 㐠െ ሼ ， 故不等式 ሼ ǡ ሼ ൅ 成立的一个充分不必要条件是 െ 1 ， 故选：A． 3.答案：D 解析： 本题考查了频率分布直方图的应用问题，是基础题． 根据频率分布直方图，算出自习时间不少于 ሼሼ. 小时的频率，再求出对应的频数． 解：自习时间不少于 ሼሼ. 小时的频率为： .16 . . ሼ. ൌ . ， 故自习时间不少于 ሼሼ. 小时的人数为： . ሼ ൌ 1 ， 故选：D． 4.答案：A 解析： 本题考查函数的单调性和奇偶性，以及函数的图象的判断，考查分析问题解决问题的能力，属于基 础题． 先判断函数的奇偶性，然后用定义法判断函数在 上的单调性，排除选项 B，C，D． 解：设函数 ൌ ൌ ሼ െ െ1 ， 则 െ ൌ െ ሼ െ െ െ1 ൌൌ ሼ െ െ1 ൌ ， 所以 为偶函数，排除 D 选项， 设 1 ൅ ሼ ൅ ， 1 െ ሼ ൌ 1 ሼ െ 1 െ1 െ ሼ ሼ െ ሼ െ1 ൌ 1 ሼ 1 1 െ ሼ ሼ ሼ 1 ， 1 ൅ ሼ ൅ ， ൌ ሼ 1 在 上单调递增， 1 ሼ 1 1 െ ሼ ሼ ሼ 1 ൅ ， 即 1 െ ሼ ൅ ， 在 上单调递增，排除 B，C， 故选 A． 5.答案：B 解析：解：如图，在 棱 中 ൌ 棱 ൌ ሼ ， 棱 ൌ 1ሼ ， 可得 棱 ൌ ሼ ǡ ， 由正弦定理，可得 棱 外接圆半径 ， 设此圆圆心为 ，球心为 O，在 中， 易得球半径 ൌ ， 故此球的表面积为 ሼ ൌ ሼ ． 故选：B． 通过已知条件求出底面外接圆的半径，设此圆圆心为 ，球心为 O，在 中，求出球的半 径，然后求出球的表面积． 本题考查三棱柱的外接球，考查正余弦定理在解三角形中的应用，考查球的表面积公式，属于中档 题． 6.答案：B 解析：解： ൌെ ， െ ൌെ െ ൌെ ൌ െ ൌ ， 函数 是偶函数 答案选：B 直接根据偶函数的定义判断即可 本题考查函数奇偶性，属于基础题． 7.答案：A 解析：解： 若 图象上相邻两条对称轴之间的距离为 ， 三角函数的周期 ൌ ሼ ，即 ൌ ሼ ൌ ሼ ，即 ൌ 1 ， 则 ൌ sin ， 当 ൌ 6 时， 取得最大值， 即 6 ൌ sin 6 ൌ 1 ， 即 6 ൌ ሼ ሼ洠 ， 即 ൌ ǡ ሼ洠 ， ሼ ， ൌ ǡ ， 则 ൌ sin ǡ ， 当 6 6 ， 则 ǡ ሼ ǡ ሼ ，此时函数单调递减， 即 在 6 6 上是减函数， 故选：A 根据三角函数的图象和性质，分别求出周期，利用正弦函数的单调性即可得到结论． 本题主要考查三角函数的图象和性质，利用条件求出函数的解析式是解决本题的关键． 8.答案：D 解析：解：根据题意，双曲线 ሼ െ ሼ ൌ 1 与抛物线 ሼ ൌ 的一个交点为 P，设 P 的坐标为 抛物线的方程为 ሼ ൌ ， 其准线为 ൌെ ሼ ， 若 晦䁪 ൌ ，则 P 到准线 ൌെ ሼ 的距离为 5，则 ൌ ǡ ， 则有 ሼ ൌ ǡ ，解可得 ൌ ሼ 6 ， 即 晦ǡ ሼ 6 ， 又由 P 在双曲线上，则有 െ ሼ ൌ 1 ，解可得 ൌ ǡ ， 则双曲线的方程为： ሼ െ ሼ ǡ ൌ 1 ， 其中 ൌ 1 ， ൌ ǡ ，则 h ൌ 1 ǡ ൌ ሼ ， 其离心率 ൌ h ൌ ሼ ； 故选：D． 根据题意，设 P 的坐标为 ，由 晦䁪 ൌ 结合抛物线的性质分析可得 ൌ ǡ ，代入抛物线的方 程可得 的值，即可得 P 的坐标，将 P 的坐标代入双曲线的方程，计算可得 m 的值，即可得双曲线 的标准方程，由双曲线离心率公式计算可得答案． 本题考查抛物线、双曲线的几何性质，关键是求出 P 的坐标． 9.答案：C 解析： 本题考查了函数图象的运用，运用图象判断函数零点的问题，考查了数形结合思想，属于中档题． 作出函数图象，确定关键的点，再结合图象判断即可． 解：易知当 ൅െ 1 时，函数 ， ， 易知此时当 ൌെ 1 ሼ 时， ൌ ， 所以此时 有一个零点， 要使 ൌ 1 有三个零点， 即使函数 ൌ 1 ൌ ሼ 1 在 െ 1 处有两个零点， 此时 ൌ 等价于 ൌെ ሼ െ െ 1 ൌെ ሼ ሼ ǡ 在 െ 1 处有两个零点， 即等价于函数 ൌ 与函数 ൌെ ሼ െ െ 1 ൌെ ሼ ሼ ǡ 在 െ 1 处有两个交点， 作出函数图象如下： 要使函数 ൌ 与函数 ൌെ ሼ െ െ 1 ൌെ ሼ ሼ ǡ 在 െ 1 处有两个交点， 结合图象可知 ሼ 㐠 ǡ ， 故选 C． 10.答案： െ ሼ െ 解析： 利用复数的四则运算即可得出． 本题考查了复数的四则运算，属于基础题． 解：原式 ൌ ሼ െሼെሼ ൌ ሼ െ ൌെ ሼ െ ． 故答案为： െ ሼ െ ． 11.答案：40 解析： 本题考查二项展开式的特定项与特定项的系数． 求出二项展开式的通项，计算可得结果． 解：根据题意得， 1 ൌ 棱 ሼ െ ሼ ൌ 棱 ሼ 1െǡ ， 令 1 െ ǡ ൌ ，得 ൌ ሼ ， ሼ ሼ 的展开式中 的系数为 棱 ሼ ሼ ሼ ൌ ． 故答案为 40． 12.答案： െ ሼ ሼ െ 1 ሼ ൌ 1 解析： 本题考查由条件求圆的标准方程，属于基础题． 解： 点 ሼ ， ǡ െ ሼ ， 的中点坐标为 ， 洠 ൌ ሼሼ െǡ ൌ ሼ ， 的垂直平分线方程为 ൌെ 1 ሼ െ ， 圆心在直线 ሼ െ െ ǡ ൌ 上， 由 ሼ െ െ ǡ ൌ ൌെ 1 ሼ െ 得 ൌ ሼ ൌ 1 ，即圆心为 ሼ1 ， 半径 ൌ െ ሼ ሼ ሼ െ 1 ሼ ൌ 1 ， 所以圆的方程为 െ ሼ ሼ െ 1 ሼ ൌ 1 ． 故答案为 െ ሼ ሼ െ 1 ሼ ൌ 1 ． 13.答案： ሼ ǡ ； ሼ 解析： 表示取出的 2 个球中红球的个数，则 的所有可能取值为 0、1，得到概率，然后求出期望与方差． 解： 可取 0、1，且 晦 ൌ ൌ 1 ǡ ， 晦 ൌ 1 ൌ ሼ ǡ ， 所以 ൌ 1 ǡ 1 ሼ ǡ ൌ ሼ ǡ ． ൌ െ ሼ ǡ ሼ 1 ǡ 1 െ ሼ ǡ ሼ ሼ ǡ ൌ ሼ ． 故答案为： ሼ ǡ ； ሼ ． 14.答案：4 解析：解：由 1 ൌ ሼ 可得， ൌ ሼ ሼ ， 所以 当且仅当 ൌ ， ൌ 1 时取等号 ． 故答案为：4． 先将 1 ൌ ሼ 整理成 ൌ ሼ ，再利用基本不等式的性质即可得解． 本题考查基本不等式的应用，属于基础题． 15.答案：1 解析：解：如图， 䁪 ൌ 䁪 ， 䁪 ൌ 棱 棱䁪 ； 所以根据点 E，F 分别是边 AD，BC 的中点，两式相加得： ሼ䁪 ൌ 棱 ； 等式两边平方得 䁪 ሼ ൌ ሼ ሼ 棱 棱 ሼ ； ൌ 1 ሼ 棱 ； 棱 ൌ 1 ． 故答案为：1． 根据向量的加法表示出向量 䁪 ： 䁪 ൌ 䁪 ， 䁪 ൌ 棱 棱䁪 ，根据已知条件有 ൌ 䁪 棱䁪 ൌ ，所以对上面两等式相加得 ሼ䁪 ൌ 棱 ，两边平方即可出现 棱 并将其求 出． 考查向量加法的几何意义，以及向量数量积的运算，要求 棱 而先去构造出 棱 的方法． 16.答案：解： Ⅰ െ棱 ൌ െ h ， 在 棱 中，由正弦定理得： െh ൌ െ h ， 即 ሼ െ h ሼ ൌ െ ሼ ， 由余弦定理得： h݋棱 ൌ ሼ ሼ െh ሼ ሼ ൌ 1 ሼ ， 又 角 C 是三角形 ABC 的内角， 棱 ൌ ǡ ； Ⅱ 由 h݋ ൌ 1 及 sin ሼ cos ሼ ൌ 1 得 ൌ 1 െ cos ሼ ൌ 1 െ 1 ሼ ൌ ǡ ， h݋ሼ ൌ ሼh݋ ሼ െ 1 ൌെ ， ሼ ൌ ሼh݋ ൌ ሼ ǡ 1 ൌ ǡ ， cosሼ െ 棱 ൌ cosሼ െ ǡ ൌ h݋ሼh݋ ǡ ሼ ǡ ൌെ 1 ሼ ǡ ǡ ሼ ൌെ ሼǡ ． 解析：本题考查的知识点是正弦定理，两角和与差的余弦公式，诱导公式，属于中档题． Ⅰ 利用正弦定理得到 ሼ െ h ሼ ൌ െ ሼ ，再结合余弦定理和特殊角的三角函数求得 C 的值； Ⅱ 由同角三角函数关系，二倍角公式进行转化并求值． 17.答案： 1 证明：由 晦 平面 ABCD， 平面 ABCD，得 晦 ， 又 晦 ， 晦 晦 ൌ 晦 ，AP， 晦 平面 APD， 所以 平面 APD， 又 平面 APD， 所以 ， 又 䁠䁠棱 ， 所以 棱 ， 因为 晦 平面 ABCD， 棱 平面 ABCD， 所以 晦 棱 ， 又 晦 ൌ ，BD， 晦 平面 PDB， 所以 棱 平面 PDB； ሼ 解：由 1 可知 ，又 ൌ ሼ ， ൌ ， 所以 ൌ ൌ 1 ， 又 平面 APD， 所以 DP 为 BP 在平面 APD 内的射影，故 晦 ൌ ， 所以 晦 ൌ ൌ 1 ， 以 D 为坐标原点，DA，DB，DP 所在直线为 x 轴，y 轴，z 轴，建立空间直角坐标系， 则 晦 0， 1 ， 1 0， ， 1， ， 棱 െ 1 1， ， 所以 晦 ൌ 1 െ 1晦棱 ൌ െ 11 െ 1 ， 晦 ൌ 1 െ 1 ， 设 ൌ 为平面 APC 的法向量， 则 晦棱 ൌെ െ ൌ 晦 ൌ െ ൌ ，故 ൌ 1ሼ1 ， 设平面 PCB 的法向量 ൌ h ， 则 晦棱 ൌെ െ h ൌ 晦 ൌ െ h ൌ ，得 ൌ 11 ， 故 cos 㐠 ൅ൌ ǡ ሼ ǡ ൌ ǡ ሼ ， 因为二面角 െ 晦棱 െ 为锐二面角， 所以二面角 െ 晦棱 െ 的大小为 6 ． 解析：本题考查线面垂直的判定定理与性质定理，考查空间想象能力和运算能力，是中档题． 1 根据题意，先判断 平面 APD，得到 晦 棱 ，根据线面垂直的判定定理得出结论； ሼ 根据题意，以 D 为坐标原点，DA，DB，DP 所在直线为 x 轴，y 轴，z 轴，建立空间直角坐标系， 求出平面 APC 和平面 PCB 的法向量，进行求解即可． 18.答案：解： 1 设 是公比 q 不为 1 的等比数列， 1 为 ሼ ， ǡ 的等差中项，可得 ሼ1 ൌ ሼ ǡ ， 即 ሼ1 ൌ 1 1 ሼ ， 即为 ሼ െ ሼ ൌ ， 解得 ൌെ ሼ ൌ 1 舍去 ， 所以 的公比为 െ ሼ ； ሼ 若 1 ൌ 1 ，则 ൌ െ ሼ െ1 ， ൌ െ ሼ െ1 ， 则数列 的前 n 项和为 ൌ 11 ሼ െ ሼ ǡ െ ሼ ሼ െ ሼ െ1 ， െ ሼ ൌ 1 െ ሼ ሼ െ ሼ ሼ ǡ െ ሼ ǡ െ ሼ ， 两式相减可得 ǡ ൌ 1 െ ሼ െ ሼ ሼ െ ሼ ǡ െ ሼ െ1 െ െ ሼ ൌ 1െെሼ 1െെሼ െ െ ሼ ， 化简可得 ൌ 1െ1ǡെሼ ． 所以数列 的前 n 项和为 1െ1ǡെሼ ． 解析：本题考查等比数列的通项公式和求和公式的运用，以及等差数列的中项性质，考查数列的错 位相减法求和，主要考查方程思想和化简运算能力，属于中档题． 1 设 是公比 q 不为 1 的等比数列，运用等差数列的中项性质和等比数列的通项公式，解方程可 得公比 q； ሼ 求得 ， ，运用数列的数列的错位相减法求和，结合等比数列的求和公式，化简整理，可得 所求和． 19.答案：解： Ⅰ 因为椭圆的焦点在 x 轴上， ൌ ሼ ，离心率 ൌ ǡ ሼ ， 所以 ൌ 1 ， h ൌ ǡ ሼ . 所以由 ሼ ൌ ሼ h ሼ ，得 ሼ ൌ ． 所以椭圆 C 的标准方程是 ሼ ሼ ൌ 1 ． Ⅱ 设点 P 的坐标为 ，所以 Q 的坐标为 െ . 因为 M，N 分别是 OP，BP 的中点， 1 ， െ 1 ， 所以 M 点的坐标为 ሼ ሼ ，N 点的坐标为 ሼ െ1 ሼ ． 所以直线 AD 的方程为 ൌ െሼ 1 ． 代入椭圆方程 ሼ ሼ ൌ 1 中，整理得 ሼ െ ሼ ሼ ሼ െ ሼ ൌ ． 所以 ൌ ，或 ൌ ሼെ ሼ െሼ ሼ ൌ ሼሼെ െ ． 所以 ൌ െሼ ሼሼെ െ 1 ൌ െሼ ሼ െǡ െ ． 所以 D 的坐标为 ሼሼെ െ െሼ ሼ െǡ െ ． 所以 洠 ൌ െ1 ሼ െ ሼ ൌെ 1 ǡ ． 又 洠 ൌ െሼ ሼെǡ െ െ ሼሼെ െ ൌ 1ሼെǡ ǡǡെሼ ൌെ 1 ǡ ൌ 洠 ． 所以 D，N，Q 三点共线． 解析： Ⅰ 通过椭圆的焦点在 x 轴上， ൌ ሼ ，离心率 ൌ ǡ ሼ ，求出 a，b，然后求解椭圆方程． Ⅱ 设点 P 的坐标为 ，所以 Q 的坐标为 െ . 求出 M 点的坐标为 ሼ ሼ ，N 点的坐标为 ሼ െ1 ሼ ，得到直线 AD 的方程，代入椭圆方程．求出 D 的坐标然后根据斜率相等证明 D，N，Q 三点共线． 本题考查椭圆方程的求法，直线与椭圆的位置关系的综合应用，考查计算能力． 20.答案：解： 1 函数 ൌ ሼ െ 1 െ 的导数为 ൌ ሼ െ 1 ൌ ሼ ሼ െ1 ， 当 时， 㐠 ， 在 为减函数； 当 ൅ 时， ൌ 可得 ൌ 1 ሼ ， 当 㐠 㐠 1 ሼ 时， 㐠 ；当 ൅ 1 ሼ 时， ൅ ． 可得 在 1 ሼ 为减函数，在 1 ሼ 为增函数， 综上可得，当 时， 在 为减函数； 当 ൅ 时， 在 1 ሼ 为减函数，在 1 ሼ 为增函数； ሼ 对 1 成立， 可得 ሼ 1 ， 当 ൅ 1 时， 1 ሼ 1 ሼ ， 令 ൌ 1 ሼ 1 ሼ ， ൌെ ሼ ǡ െ 1 ሼ 1െሼ ǡ ൌ െ1െെሼ ǡ ， 当 1 时， െ 1 െ െ ሼ 㐠 ，即 㐠 ， 在 1 递减， 可得 1 ൌ ሼ ， 则 a 的取值范围是 ሼ ． 解析： 1 求出 的导数，讨论当 时，当 ൅ 时，由导数大于 0，可得增区间；导数小于 0，可得减区间； ሼ 由题意可得 ሼ 1 ，当 ൅ 1 时， 1 ሼ 1 ሼ ，令 ൌ 1 ሼ 1 ሼ ，求出导数， 判断单调性，可得 的最大值，可得 a 的范围． 本题考查导数的运用：求单调性，注意运用分类讨论的思想方法，考查不等式恒成立问题的解法， 注意运用参数分离和构造函数法，考查转化思想和运算能力，属于中档题．