2020_2021学年新教材高中数学第五章三角函数5 47页

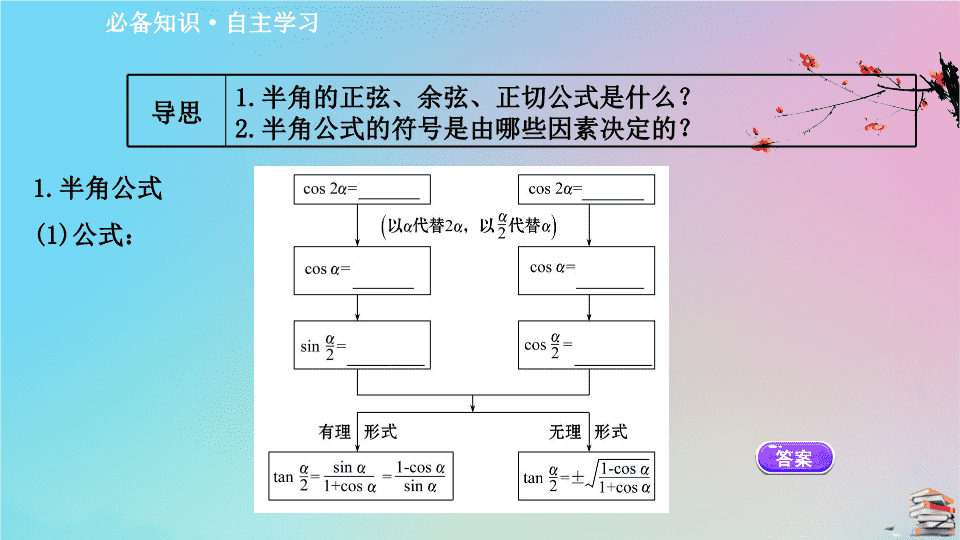
5.5.2 　简单的三角恒等变换 ( 一 ) 必备知识 · 自主学习 1. 半角公式 (1) 公式： 导思 1. 半角的正弦、余弦、正切公式是什么？ 2. 半角公式的符号是由哪些因素决定的？ (2) 本质： ①半角公式的正弦、余弦公式实际上是由二倍角公式变形得到的 . ② 半角公式给出了求 的正弦、余弦、正切的另一种方式，即只需知道 cos α 的值及相应 α 的条件，便可求出 sin ， cos ， tan . (3) 应用：①求值；②化简；③证明 . 【 思考 】 (1) 半角公式中的正负号能否去掉？该如何选择？ 提示： 不能 .① 若没有给出决定符号的条件，则在根号前保留正负两个符号； ②若给出 α 的具体范围 ( 即某一区间 ) 时，则先求 所在范围，然后根据 所在 范围选用符号 . (2) 半角公式对 α∈R 都成立吗？为什么？ 提示： 公式 对 α∈R 都成立，但公式 要求 α≠(2k+1)π(k∈Z). 2. 辅助角公式 (1) 公式 asin x+bcos x= sin(x+θ). (2) 本质：辅助角公式实际是两角和与差的正弦、余弦公式的逆用，它能把不同名的弦函数的和差转化成同名的弦函数，进而利用三角函数的性质解决问题 . (3) 应用：①化简；②求值 . 【 思考 】 (1)asin x+bcos x 化简的步骤有哪些？ (2) 在上述化简过程中，如何确定 θ 所在的象限？ 提示： (1)① 提常数，提出 得到 ②定角度，确定一个角 θ 满足： cos θ= ( 或 (sin θsin x+cos θcos x)). ③ 化简、逆用公式得 asin x+bcos x= sin(x+θ)( 或 asin x+bcos x= cos(x-θ)). (2)θ 所在的象限由 a 和 b 的符号确定 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) ( 　　 ) (2) 存在 α∈R ，使得 cos = cos α. ( 　　 ) (3) 对于任意 α∈R ， sin = sin α 都不成立 . ( 　　 ) (4) 若 α 是第一象限角，则 tan = . ( 　　 ) 提示： (1)×. 只有当 - +2kπ≤ ≤ +2kπ(k∈Z) ， 即 -π+4kπ≤α≤π+4kπ(k∈Z) 时， cos = . (2)√. 当 cos α=- +1 时，上式成立，但一般情况下不成立 . (3)×. 当 α=2kπ(k∈Z) 时，上式成立，但一般情况下不成立 . (4)√. 若 α 是第一象限角，则 是第一、三象限角，此时 tan = 成立 . 2.( 教材二次开发：例题改编 ) 若 cos α= ， α∈(0 ， π) ，则 cos 的值为 ( 　　 ) 　　　　　　　　　　　　　　　　　　 【 解析 】 选 C. 因为 ∈ ，所以 cos >0 ， cos = = . 3.cos α-sin α 的化简结果是 ( 　　 ) 【 解析 】 选 D.cos α-sin α= 关键能力 · 合作学习 类型一　求值问题 ( 数学运算 ) 【 题组训练 】 1. 设 5π<θ<6π ， cos =a ，那么 sin 等于 ( 　　 ) 　　　　　　　　　　　　　　　　　　 2. 已知 α∈ ， cos α= ，则 tan = ( 　　 ) A.3 B.-3 C. D.- 3. 已知 tan α= ，且 α 为第一象限角，则 sin 的值为 ( 　　 ) 【 解析 】 1. 选 D. 若 5π<θ<6π ，则 则 2. 选 D. 因为 α∈ ，且 cos α= ，所以 ∈ ， tan = 3. 选 C. 因为 tan α= ，所以 又 sin 2 α+cos 2 α=1 ， 所以 因为 α 为第一象限角， 所以 为第一、三象限角，且 【 解题策略 】 利用半角公式求值的思路 (1) 看角：若已知三角函数式中的角是待求三角函数式中角的两倍，则求解时常常借助半角公式求解 . (2) 明范围：由于半角公式求值常涉及符号问题，因此求解时务必依据角的范围，求出相应半角的范围 . (3) 选公式：涉及半角公式的正切值时，常用 tan = 其优点是计算时可避免因开方带来的求角的范围问题；涉及半角公式的正、 余弦值时，常先利用 计算 . (4) 下结论：结合 (2) 求值 . 【 补偿训练 】 已知 sin α=- ， π<α< ，求 sin ， cos ， tan 的值 . 【 解析 】 因为 π<α< ， sin α=- ，所以 cos α=- ， 且 类型二　化简问题 ( 数学运算 ) 【 典例 】 化简： 【 思路导引 】 利用二倍角公式及半角公式解决，注意角度的范围 . 【 解析 】 原式 = 又因为 180°<α<360° ， 所以 90°< <180° ， 所以 cos <0 ， 所以原式 = =cos α. 【 解题策略 】 化简问题中的“三变” (1) 变角：三角变换时通常先寻找式子中各角之间的联系，通过拆、凑等手段消除角之间的差异，合理选择联系它们的公式 . (2) 变名：观察三角函数种类的差异，尽量统一函数的名称，如统一为弦或统一为切 . (3) 变式：观察式子的结构形式的差异，选择适当的变形途径 . 如升幂、降幂、配方、开方等 . 【 跟踪训练 】 化简： 【 解析 】 原式 因为 π<α< ， 所以 所以 cos <0 ， sin >0. 所以原式 【 拓展延伸 】 　　　 1. 积化和差公式 sin αcos β= cos αsin β= cos αcos β= sin αsin β= 2. 和差化积公式 sin θ+sin φ = sin θ-sin φ = cos θ+cos φ = cos θ -cos φ = 【 拓展训练 】 求值 ： sin 2 20°+cos 2 80°+ sin 20°cos 80°. 【 解析 】 sin 2 20°+cos 2 80°+ sin 20°cos 80° 类型三　恒等式的证明问题 ( 数学运算、逻辑推理 ) 　角度 1 　绝对恒等式的证明  【 典例 】 求证： 【 思路导引 】 左边切化弦，通分，变形，直至与右边相等 . 【 证明 】 因为左边 = 所以原式成立 . 【 变式探究 】 若本例变为：求证： =tan x ，试证明 . 【 证明 】 因为左边 = 所以原式成立 . 　角度 2 　条件恒等式的证明  【 典例 】 已知 0<α< ， 0<β< ，且 3sin β=sin(2α+β) ， 4tan =1-tan 2 . 证明： α+β= . 【 思路导引 】 结合已知条件，求 α+β 的某个三角函数值，进而求出角的大小 . 【 证明 】 因为 3sin β=sin(2α+β) ， 即 3sin(α+β-α)=sin(α+β+α) ， 所以 3sin(α+β)cos α-3cos(α+β)sin α =sin( α + β )cos α +cos( α + β )sin α ， 所以 2sin( α + β )cos α =4cos( α + β )sin α ，所以 tan( α + β )=2tan α . 又因为 4tan =1-tan 2 ， 所以 tan α = 所以 tan( α + β )=2tan α =1. 因为 α+β∈ ，所以 α+β= . 【 解题策略 】 (1) 证明三角恒等式的实质是消除等式两边的差异，有目的的化繁为简、左右归一 . (2) 三角恒等式的证明主要有两种类型：绝对恒等式与条件恒等式 . ① 证明绝对恒等式要根据等式两边的特征，化繁为简，左右归一，通过三角恒等式变换，使等式的两边化异为同 . ② 条件恒等式的证明则要认真观察，比较已知条件与求证等式之间的联系，选择适当途径 . 常用代入法、消元法、两头凑等方法 . 【 题组训练 】 1. 求证： 2sin 4 x+ sin 2 2x+5cos 4 x- (cos 4x+cos 2x)=2(1+cos 2 x). 【 证明 】 左边 = 所以原等式成立 . 2. 已知 sin β =msin(2 α + β )(m≠1) ， 求证： tan( α + β )= tan α . 【 证明 】 由 β=(α+β)-α ， 2α+β=(α+β)+α 得 sin[ (α ＋ β) － α] =m · sin[ (α ＋ β) ＋ α] ， 即 sin(α+β)cos α-cos(α+β)sin α =m[ sin(α ＋ β)cos α ＋ cos(α ＋ β)sin α] ， 即 (1-m)sin(α+β)cos α=(1+m)cos(α+β)sin α. 两边同除以 (1-m)cos(α+β)cos α ， 得 tan(α+β)= tan α(m≠1) ，即原等式成立 . 【 补偿训练 】 已知 sin α=Asin(α+β) ， |A|>1. 求证： tan(α+β)= . 【 证明 】 因为 sin α=sin[ (α ＋ β) － β] =sin(α+β)cos β-cos(α+β)sin β ， 所以 sin α=Asin(α+β) 化为 sin(α+β)cos β-cos(α+β) · sin β =Asin(α+β) ， 所以 sin(α+β)(cos β-A)=cos(α+β)sin β ，又因为 |A|>1 ， 所以 tan(α+β)= 课堂检测 · 素养达标 1. 已知 cos α=- ， <α<π ，则 sin 等于 ( 　　 ) 　　　　　　　　　　　　　　　　　　 【 解析 】 选 D. 因为 <α<π ，所以 2.( 教材二次开发：练习改编 ) 已知 cos θ=- (-180°<θ<-90°) ，则 cos = ( 　　 ) 【 解析 】 选 B. 因为 -180°<θ<-90° ，所以 -90°< <-45°. 又 cos θ= 3. 化简 的结果是 ( 　　 ) A.-cos 1 B.cos 1 C. cos 1 D.- cos 1 【 解析 】 选 C. 原式 = 4. 若 sin +2cos =0 ，则 tan θ=_______.  【 解析 】 由 sin +2cos =0 ，得 tan =-2 ， 答案： 5. 化简 =_______.  【 解析 】 原式 = 答案：