2020届河南省实验中学高三12月月考数学（文）试题 9页

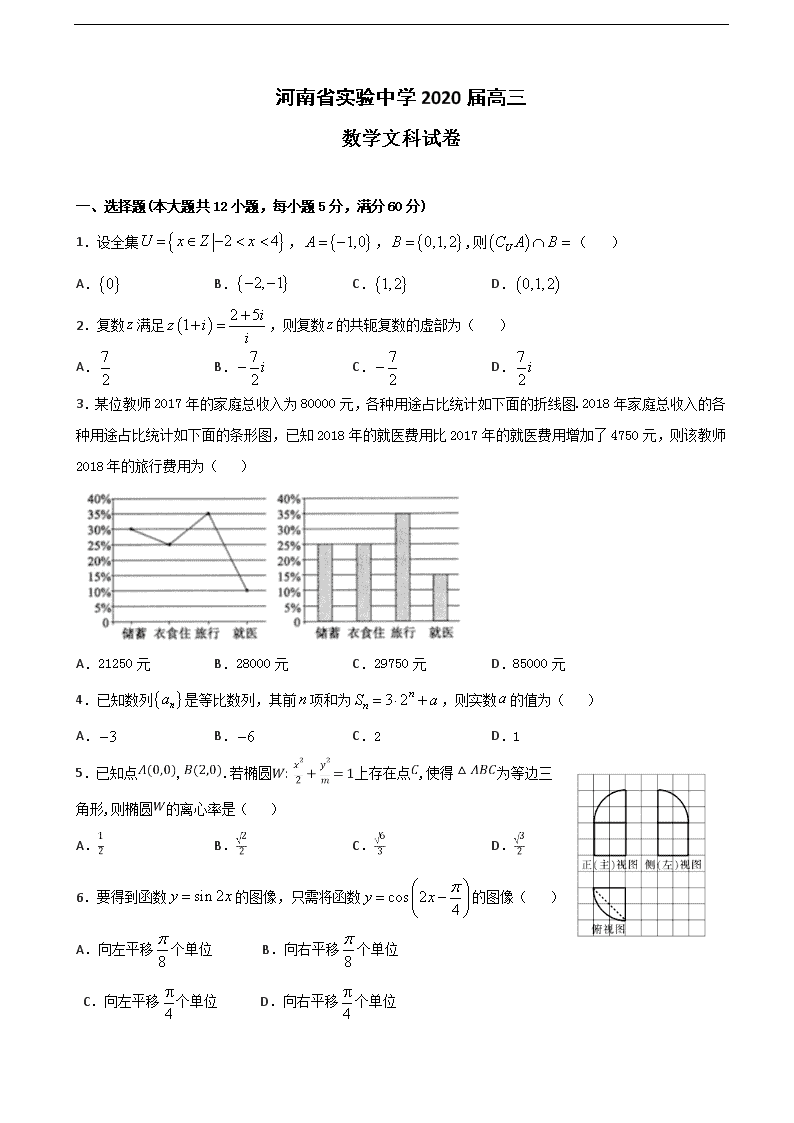
河南省实验中学2020届高三 数学文科试卷 一、选择题(本大题共12小题，每小题5分，满分60分)‎ ‎1．设全集，，,则（ ）‎ A． B． C． D．[来源:Zxxk.Com]‎ ‎2．复数满足，则复数的共轭复数的虚部为（ ）‎ A． B． C． D．‎ ‎3．某位教师2017年的家庭总收入为80000元，各种用途占比统计如下面的折线图.2018年家庭总收入的各种用途占比统计如下面的条形图，已知2018年的就医费用比2017年的就医费用增加了4750元，则该教师2018年的旅行费用为（ ）‎ A．21250元 B．28000元 C．29750元 D．85000元 ‎4．已知数列是等比数列，其前项和为，则实数的值为（ ）‎ A． B． C．2 D．1‎ ‎5．已知点,.若椭圆上存在点,使得为等边三角形,则椭圆的离心率是（ ）‎ A． B． C． D．‎ ‎6．要得到函数的图像，只需将函数的图像（ ）‎ A．向左平移个单位 B．向右平移个单位 ‎ ‎ C．向左平移个单位 D．向右平移个单位 ‎7．如图网格纸中小正方形的边长为，粗线画出的是某几何体的三视图，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎8．函数，则使得成立的取值范围是（ ）‎ A. B。 C。 D。 ‎ ‎9．如图,正方体的棱长为1,动点E在线段上,F、M分别是AD、CD的中点,则下列结论中错误的是(     )‎ A．‎ B．平面 C．存在点E,使得平面//平面 D．三棱锥的体积为定值 ‎10．已知数列的前项和，数列满足，记数列的前项和为，则（ ）‎ A．2016 B．2017 C．2018 D．2019‎ ‎11．一段1米长的绳子，将其截为3段，问这三段可以组成三角形的概率是（ ）‎ A． B． C． D．‎ ‎12．已知函数与函数的图象在区间上恰有两对关于轴对称的点，则实数m的取值范围是( )‎ A． B． C． D．‎ 二、填空题(本大题4小题，每小题5分，共20分)‎ ‎13．已知，则在的投影是__________[来源:学科网]‎ ‎14．已知函数与直线相切，则的取值是_________． （15题图）‎ ‎15．已知矩形的长，宽，将其沿对角线折起，得到四面体，如图所示：[来源:学科网]‎ 则四面体体积的最大值为____________.‎ ‎16．已知双曲线的左、右焦点分别为，，点是双曲线左支上的一点，若直线与直线平行且的周长为，则双曲线的离心率为______.‎ 三、解答题：（共70分，第17—21题为必考题，每题12分；22,23题为选考题，每题10分）‎ ‎17．(本题满分12分)《中华人民共和国道路交通安全法》第47条的相关规定：机动车行经人行横道时，应当减速慢行；遇行人正在通过人行横道，应当停车让行，俗称“礼让斑马线”，《中华人民共和国道路交通安全法》第90条规定：对不礼让行人的驾驶员处以扣3分，罚款50元的处罚．‎ ‎（1）交警从这5个月内通过该路口的驾驶员中随机抽查了50人，调查驾驶员不“礼让斑马线”行为与驾龄的关系，得到如下列联表：能否据此判断有97.5%的把握认为“礼让斑马线”行为与驾龄有关？‎ 不礼让斑马线 礼让斑马线 合计 驾龄不超过1年 ‎22‎ ‎8‎ ‎30‎ 驾龄1年以上 ‎8‎ ‎12‎ ‎20‎ 合计 ‎30‎ ‎20‎ ‎50‎ ‎（2）下图是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为的折线图：‎ 请结合图形和所给数据求违章驾驶员人数y与月份x之间的回归直线方程，并预测该路口7月份的不“礼让斑马线”违章驾驶员人数．‎ 附注：参考数据：，．‎ 参考公式：，，（其中）‎ ‎0.150‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.072[来源:Z*xx*k.Com]‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎18．(本题满分12分)已知是一个公差大于的等差数列，且满足，数列满足等式： ‎ ‎（1）求数列的通项公式； （2）求数列的前项和.‎ ‎19．(本题满分12分)如图，四棱锥P一ABCD中，AB=AD=2BC=2，BC∥AD，AB⊥AD，△PBD为正三角形．且PA=2．‎ ‎（1）证明：平面PAB⊥平面PBC；‎ ‎（2）若点P到底面ABCD的距离为2，E是线段PD上一点，且PB∥平面ACE，求四面体A-CDE的体积．‎ ‎20．(本题满分12分)已知函数存在极值点．‎ ‎（1）求的取值范围；‎ ‎（2）设的极值点为，若，求的取值范围．‎ ‎21．(本题满分12分)已知点，圆:，过点的动直线与圆交于两点，线段的中点为，为坐标原点.‎ ‎(1)求的轨迹方程； (2)当时，求的方程及的面积 选做题 ‎22．(本题满分10分)如图，在极坐标系中，，，，，弧，，所在圆的圆心分别是，，，曲线是弧，曲线是弧，曲线是弧.‎ ‎（1）分别写出，，的极坐标方程；‎ ‎（2）曲线由，，构成，若点在上，且，求的极坐标.‎ ‎23．(本题满分10分)设，且.‎ ‎（1）求的最小值；‎ ‎（2）若成立，证明：或.‎ 河南省实验中学2020届高三 数学文科试卷 参考答案 一、选择题：1．C 2．A 3．C 4．A 5．C 6．B 7．C 8．B 9．C 10．A 11．A 12．A 二、填空题：13． 14． 15． 16．2‎ ‎17．解：（1）由列联表中数据，计算，‎ 由此能判断有97.5%的把握认为“礼让斑马线”行为与驾龄有关 ‎（2）利用所给数据，计算，‎ ‎；‎ ‎；‎ ‎∴与之间的回归直线方程；‎ 当时，，‎ 即预测该路口7月份的不“礼让斑马线”违章驾驶员有66人．‎ ‎18．（1）在等差数列中，由，得，‎ 又，可得或．，，则．‎ ‎.‎ ‎（2）由，‎ 得，，即，‎ 满足上式，．则，‎ 数列的前项和，‎ ‎．‎ ‎19．（1），且，，‎ 又为正三角形，，又，，‎ ‎，，又，，，，‎ 平面，又平面，‎ 平面平面． ‎ ‎（2）如图，设，交于点，，‎ 且，，连接，‎ 平面，，则，‎ 又点到平面的距离为2，‎ 点到平面的距离为，‎ ‎，‎ 即四面体的体积为．‎ ‎20．（1）函数的定义域为，，‎ 当时，，即函数单调递减，无极值点； 当时，由或，‎ 设，则 当时，的两根一个小于1、一个大于1，故有一个极值点；‎ 当时，由对称轴为，知的两根均小于1，故无极值点；‎ 综上所述，；‎ ‎（2）由（1）知且，∴，‎ 令，显然在上单增，‎ 又，∴即，‎ ‎∴， ∴.‎ ‎21．（1）圆C的方程可化为，所以圆心为，半径为4，‎ 设，则，，‎ 由题设知，故，即.[来源:学科网]‎ 由于点P在圆C的内部，所以M的轨迹方程是.‎ ‎（2）由（1）可知M的轨迹是以点为圆心，为半径的圆.‎ 由于，故O在线段PM的垂直平分线上，又P在圆N上，从而.‎ 因为ON的斜率为3，所以的斜率为，故的方程为.‎ 又，O到的距离为，，所以的面积为.‎ ‎22．(1)由题意得，这三个圆的直径都是2，并且都过原点.‎ ‎，‎ ‎,.‎ ‎(2)解方程得，此时P的极坐标为 解方程得或，此时P的极坐标为或 解方程得，此时P的极坐标为 故P的极坐标为,,,.‎ ‎23．‎