【数学】2019届一轮复习北师大版直观图学案 3页

‎ 2019年高考数学总复习 ‎ ‎ ‎ 旋转体，多面体与直观图 考点一。旋转体，多面体　‎ ‎1．（1）用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是(　　)‎ A．圆柱 B．圆锥 C．球体 D．圆柱、圆锥、球体的组合体 解 选C　由球的性质可知，用平面截球所得的截面都是圆面．‎ ‎（2）下列结论中正确的是(　　)‎ A．各个面都是三角形的几何体是三棱锥、‎ B．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥 C．棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是六棱锥 D．圆锥的顶点与底面圆周上的任一点的连线都是母线 解 A错误．如图1所示，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不是棱锥．‎ B错误．如图2所示，若△ABC不是直角三角形，或是直角三角形但旋转轴不是直角边，所得的几何体不是圆锥． ‎ ‎ ‎ ‎ 图2 ‎ ‎ 图1‎ C错误．若六棱锥的所有棱都相等，则底面多边形是正六边形．但由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长．故选D.‎ ‎（3）给出下列四个命题 ‎ ‎①各侧面都是全等四边形的棱柱一定是正棱柱；②对角面是全等矩形的六面体一定是长方体；‎ ‎③棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥；④长方体一定是正四棱柱．‎ 其中正确的命题个数是(　　)‎ A．0 B．1 C．2 D．3‎ 解 选A　反例 ①直平行六面体底面是菱形，满足条件但不是正棱柱；②底面是等腰梯形的直棱柱，满足条件但不是长方体；③若以正六边形为底面，侧棱长必然要大于底面边长，故③中不能组成正六棱锥；④显然错误。‎ ‎（4）下列说法正确的是(　　)‎ A．有两个面平行，其余各面都是四边形的几何体叫棱柱 B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱 C．有一个面是多边形，其余各面都是三角形的几何体叫棱锥 D．棱台各侧棱的延长线交于一点 解 选D　由棱柱和棱锥的概念可知，A、B、C均错误．由于棱台是平行于棱锥底面的平面截棱锥，截面与底面之间的部分，故棱台各侧棱的延长线交于一点．‎ B项. 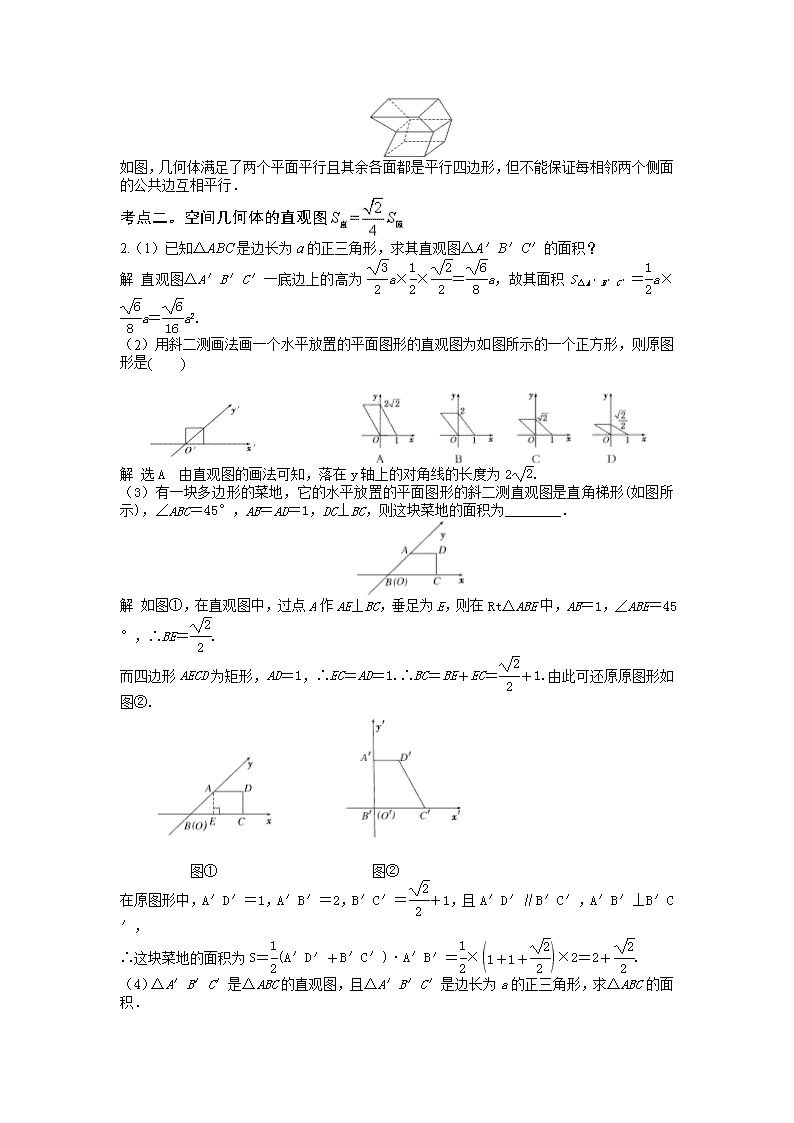‎ 如图，几何体满足了两个平面平行且其余各面都是平行四边形，但不能保证每相邻两个侧面的公共边互相平行．‎ 考点二。空间几何体的直观图 ‎2.（1）已知△ABC是边长为a的正三角形，求其直观图△A′B′C′的面积？‎ 解 直观图△A′B′C′一底边上的高为a××＝a，故其面积S△A′B′C′＝a×a＝a2.　‎ ‎（2）用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原图形是(　　)‎ ‎ ‎ 解 选A　由直观图的画法可知，落在y轴上的对角线的长度为2.‎ ‎（3）有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示)，∠ABC＝45°，AB＝AD＝1，DC⊥BC，则这块菜地的面积为________．‎ 解 如图①，在直观图中，过点A作AE⊥BC，垂足为E，则在Rt△ABE中，AB＝1，∠ABE＝45°，∴BE＝.‎ 而四边形AECD为矩形，AD＝1，∴EC＝AD＝1.∴BC＝BE＋EC＝＋1.由此可还原原图形如图②.‎ ‎ ‎ ‎　 ‎ 在原图形中，A′D′＝1，A′B′＝2，B′C′＝＋1，且A′D′∥B′C′，A′B′⊥B′C′，‎ ‎∴这块菜地的面积为S＝(A′D′＋B′C′)·A′B′＝××2＝2＋.‎ ‎（4）△A′B′C′是△ABC的直观图，且△A′B′C′是边长为a的正三角形，求△ABC的面积．‎ 解：‎ ‎△A′B′C′的顶点C′在y′轴上，A′B′边在x轴上，把y′轴绕原点逆时针旋转45°得y轴，在y轴上取点C使OC＝2OC′，A、B点即为A′、B′点，长度不变．已知A′B′＝A′C′＝a，在△OA′C′中，由正弦定理得＝，所以OC′＝a＝a，所以原三角形ABC的高OC＝a，所以S△ABC＝×a×a＝a2.‎