天津市滨海七所重点学校2021届高三上学期期末考试数学试题 Word版含答案 17页

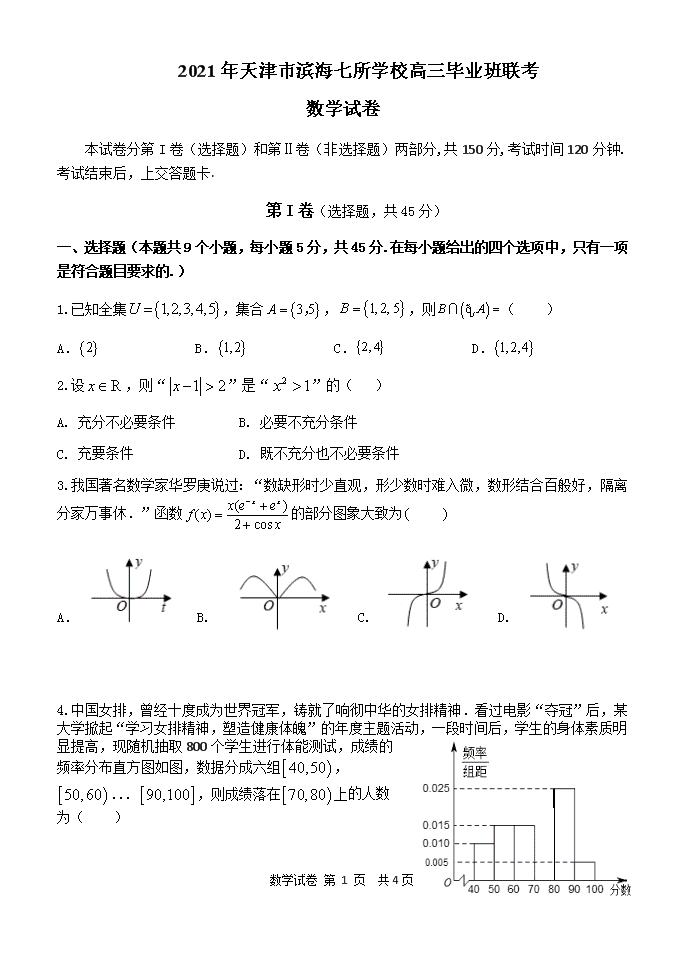
数学试卷 第 1 页 共 4 页 2021 年天津市滨海七所学校高三毕业班联考 数学试卷 本试卷分第 I 卷（选择题）和第Ⅱ卷（非选择题）两部分,共 150 分,考试时间 120 分钟. 考试结束后，上交答题卡. 第 I 卷（选择题，共 45 分） 一、选择题（本题共 9 个小题，每小题 5 分，共 45 分.在每小题给出的四个选项中，只有一项 是符合题目要求的.） 1.已知全集  1,2,3,4,5U  ，集合  3 5A  ， ，  1,2,5B  ，则  UB A  ð （ ） A． 2 B． 1,2 C． 2,4 D． 1,2,4 2.设 Rx ，则“ 21 x ”是“ 12 x ”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 3.我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离 分家万事休．”函数 ( )( ) 2 cos x xx e ef x x    的部分图象大致为 ( ) A． B. C. D. 4.中国女排，曾经十度成为世界冠军，铸就了响彻中华的女排精神．看过电影“夺冠”后，某 大学掀起“学习女排精神，塑造健康体魄”的年度主题活动，一段时间后，学生的身体素质明 显提高，现随机抽取 800 个学生进行体能测试，成绩的频 率分布直方图如图，数据分成六组 40,50 ，  50,60 ．．． 90,100 ，则成绩落在 70,80 上的人数为 （ ） A．12 B．120 数学试卷 第 2 页 共 4 页 C． 24 D． 240 5.在正方体 1 1 1 1ABCD A B C D 中，三棱锥 1 1A B CD 的表面积为 4 3 ，则正方体外接球的体 积为( ) A． 4 3 B． 6 C．  32 3 D．  8 6 6.已知函数 xexf )( ， )3 1(logefa  ， )1(log3 efb  ， )9 1(log 1 e fc  ，则下述关系式正 确的是（ ） A．b a c  B．b c a  C． c a b  D． a b c  7.已知抛物线 2 2 ( 0)y px p  上一点 (1    )M m， 到其焦点的距离为 5 ，双曲线 2 2 2 2 1x y a b   ( 0, 0)a b  的左顶点为 A 且离心率为 2 5 ，若双曲线的一条渐近线与直线 AM 垂直，则双曲线的方程为 （ ） A． 14 2 2  yx B． 14 2 2  yx C． 12 22  yx D． 14 22  yx 8.设函数   3 cos2 2sin cosf x x x x  ，给出下列结论： ①  f x 的最小正周期为 π ②  y f x 的图像关于直线 π 12x  对称 ③  f x 在 π 2,6 π 3      单调递减 ④把函数 2cos2y x 的图象上所有点向右平移 π 12 个单位长度，可得到函数  y f x 的图象。 其中所有正确结论的编号是（ ）． 数学试卷 第 3 页 共 4 页 A．①④ B．②④ C．①②④ D．①②③ 9.已知函数   2 1 log , 1( ) ( +1) 4 1 2 , af x x a x x x          ( 0a  ，且 1a  )在区间 ( , )  上为单调函数， 若函数 ( ) ( ) 2g x f x x   有三个不同的零点，则实数 a 的取值范围是（ ） A． 1 1 4 2      ， B． 1 3 4 4      ， C． 1 1 13 4 2 16           ， D． 1 3 13 4 4 16           ， 第Ⅱ卷 (非选择题，共 105 分) 二.填空题(本大题共 6 小题，每小题 5 分，共 30 分.) 10.若复数 z 满足 1 3i 1 iz   (其中i 是虚数单位)，则 z 为_____________. 11.在二项式 9 2x x     的展开式中，含 6x 的项的系数为__________. 12.已知直线l ： y x m  被圆C ： 2 2 4 02 1x xy y    截得的弦长等于该圆的半径，则 实数 m  ． 13.为了抗击新冠肺炎疫情，现从 A 医院 150 人和 B 医院 100 人中, 按分层抽样的方法，选出 5 人加入“援鄂医疗队”，现拟再从此 5 人中选出两人作为联络人，则这两名联络人中 B 医院 至少有一人的概率是________.设两名联络人中 B 医院的人数为 X ，则 X 的期望为 . 14.已知正实数 ,a b 满足 2lg( ) lg lgb aa b a b    ，则 b a ba  2 1 2 1 的最小值为__________． 15.已知平行四边形 ABCD 的两条对角线相交于点 M ， AB 2 ， AD 1 ， DAB 60  ，其 中点 P 在线段 MD 上且满足 AP CP  = 25 16  ， DP  =_______，若点 N 是线段 AB 上的动点，则 ND NP  的最小值为_______. 数学试卷 第 4 页 共 4 页 三.解答题(本大题 5 小题，共 75 分．解答应写出文字说明，证明过程或演算步骤．) 16.（本小题满分 14 分） ABC 中，角 , ,A B C 所对边分别为 , , ,a b c 且 21,cos , 5.3 ABCb c A S    （Ⅰ）求边 a 及sin B 的值； （Ⅱ）求 cos 2 6C     的值. 17.（本小题满分 15 分） 如图，在四棱锥 ABCDP  中，底面 ABCD 为直角梯形， BCAD// ， 12 1  ADBC 且 3CD ， 2PAPAFADE 的中点，是棱的中点，为 ， ,ABCDPE 底面 （Ⅰ）证明： PCDBF 平面// ； （Ⅱ）求二面角 FBDP  的正弦值； （Ⅲ）在线段 PC （不含端点）上是否存在一点 M ,使得直线 BM 和平面 BDF 所成角的正弦值为 13 39 ？若存在，求出此时 PM 的 长；若不存在，说明理由. E A P B C D F 数学试卷 第 5 页 共 4 页 18.（本小题满分 15 分） 已知椭圆 2 2 2 2: 1( 0)x yE a ba b     的离心率为 2 2 ， 1F 、 2F 分别为椭圆 E 的左、右焦点，M 为 E 上任意一点， 1 2F MFS 的最大值为 1，椭圆右顶点为 A . （Ⅰ）求椭圆 E 的方程； （Ⅱ）若过 A 的直线l 交椭圆于另一点 B ，过 B 作 x 轴的垂线交椭圆于C （C 异于 B 点），连 接 AC 交 y 轴于点 P .如果 1 2PA PB   时，求直线l 的方程． 19.（本小题满分 15 分） 设 na 是等比数列，公比大于 0， nb 是等差数列, *n N .已知 1 1a  ， 3 2 2a a  ， 4 3 5a b b  ， 5 4 62a b b  . （Ⅰ）求 na 和 nb 的通项公式； （Ⅱ）设数列 nc 满足       ,3, ,33,1,1 1 21 k k kk n na nccc 其中 k N （i）求数列 3 3( 1)n nb c  的通项公式； （ii）若 )()2)(1(         Nnnn nan 的前 n 项和为 nT ，求 )( 3 1 3     NncbT n i iin . 20.（本小题满分 16 分） 数学试卷 第 6 页 共 4 页 已知函数 2( ) 2 ln lnf x x x a x    . ( )a R （Ⅰ）令 ( ) ( )g x xf x ，讨论 ( )g x 的单调性并求极值； （Ⅱ）令 2( ) ( ) 2 lnh x f x x   ，若 ( )h x 有两个零点； （i）求 a 的取值范围； （ii）若方程 (ln ) 0xxe a x x   有两个实根 1x ， 2x ，且 1 2x x .证明： 1 2 2 1 2 x x ee x x   数学试卷 第 7 页 共 4 页 2021 年天津市滨海七所学校高三毕业班联考 数学试卷（理科） 评分标准 一、选择题（本题共 9 个小题，每小题 5 分，共 45 分） BACDB ADCD 二、填空题(本大题共 6 小题，每小题 5 分，共 30 分). 10. 5 11．144 12. 2 4或 13． 7 10 4 5 14． 1 5 2  15． 3 4 135 256 (注：两个空的答对一个空给 3 分) 三.解答题(本大题 5 小题，共 75 分．解答应写出文字说明，证明过程或演算步骤．) 16. （本小题满分 14 分） 解：（Ⅰ）因为   3 5sin,0,3 2cos  AAA 得 ， …… ………… 1 分 由 53 5 2 1sin2 1  bcAbcS ABC 得 6bc ， …… ………… 3 分 2,31  cbcb ，得由 …… ………… 4 分 53 2 2cos 222  abc acbA 得由余弦定理 …… ………… 6 分 由正弦定理 C c B b A a sinsinsin  得 1sin B …… ………… 8 分 （Ⅱ）   2,0   BBABC 由（Ⅰ）可知中，在 …… ………… 9 分 由于 3 5sincos,3 2cossin  ACAC ， …… ………… 10 分 数学试卷 第 8 页 共 4 页 ，所以 9 54 3 5 3 22cossin22sin  CCC ， 9 11cos22cos 2  CC …… ………… 12 分 .18 543 6sin2sin6cos2cos62cos        CCC所以 …… ………… 14 分 17. （本小题满分 15 分） 解：（Ⅰ）法一：取 PD 的中点为 H， ………… 1 分 连接 FH，HC.因为 F 为 PA 的中点，所以 FH // 1 2 AD ， 又因为 BC // 1 2 AD ，所以 BC // FH ,所以四边形 BCHF 为平行四边形， 所以 CBF//H ， ………… 2 分 又因为 PCD.BF//PCD,PCD,C 平面所以平面平面  BFH ………… 3 分 （Ⅰ）法二：由题意得： BC // DE , 90 ,ADC   BCDE所以四边形 为矩形， 数学试卷 第 9 页 共 4 页 ,PE ABCD又 面 ,E xyz如图建立空间直角坐标系        0 0 0 , 1,0,0 , 0, 3,0 , 1,0,0 ,E A B D 则 ，，           2 3,0,2 1,0,3,1,3,0,0 FCP …… ………… 2 分 设平面 PCD 的法向量为  zyxm ,, ，  0,3,0DC ，  3,0,1DP 0, 0 DC m DP m         则 3 0 , 3 0 y x z     则 0,则y 3,x  不妨设 1,则z ( 3,0,1)m  可得 ………… 3 分 ,02 3,3,2 1        mBFBF ，可得又 ………… 4 分 .//, BCDBFBCDBF 平面所以平面又因为直线  ……… 5 分 （Ⅱ）设平面 PBD 的法向量为  1111 ,, zyxn  ，  ,0,3,1DB  ,3,3,0 BP 则  ，可得，不妨设，即 1,1,3,3 033 03 0 0 1 11 11 1 1            nx zy yx nBP nDB …… 6 分 设平面 BDF 的法向量为  2222 ,, zyxn  ， ,2 3,0,2 3      DF 数学试卷 第 10 页 共 4 页 则  ，可得，不妨设，即 3,1,3,3 02 3 2 3 03 0 0 22 22 22 2 2            nx zx yx nDF nDB …… 7 分 因此有 1 2 1 2 1 2 7 65cos ,65 n nn n n n         ， …… ………… 8 分 （注：结果正负取决于法向量方向） 于是 ,65 654,cos1,sin 21 2 21  nnnn …… ………… 9 分 所以二面角 FBDP  的正弦值为 .65 654 …… ………… 10 分 (注：前面设角后面不写答话不扣分) （Ⅲ）设    1, 3, 3 , 3 , 3PM PC            ，…… ………… 11 分  0,1   ， 33,33,  PMBPBM …… ………… 12 分 由（Ⅱ）可知平面 BDF 的法向量为  ，3,1,32 n   ， 13 39 33213 3333333 ,cos 222 2 2          nBM nBM nBM …… ………… 13 分 有 ，0143 2   解得   ，或舍 3 11   …… ………… 14 分 可得 ，       3 3,3 3,3 1PM 数学试卷 第 11 页 共 4 页 所以 .3 7PM …… ………… 15分 18. （本小题满分 15 分） 解： （Ⅰ）当 M 为椭圆的短轴端点时， 1 2F MFS 取得最大值 即 1 2 12S c b    ； …… ………… 1 分 又因为 2 2 c a  ， 2 2 2a b c  …… ………… 2 分 解得： 2a  ， 1b  ， 1c  …… ………… 3 分 所以椭圆方程为 2 2 12 x y  …… ………… 4 分 （Ⅱ） ( 2,0)A ，根据题意，直线l 斜率存在且不为 0 设直线l ： ( 2)y k x  ， …… ………… 5 分 ( , )o oB x y 联立 2 2 ( 2) 12 y k x x y      得 2 2 2 2(1 2 ) 4 2 4 2 0k x k x k     …… ………… 6 分 2 2 4 22 1 2o kx k    ， 2 2 4 22 1 2o kx k   …… ………… 7 分 即 2 2 2 2(2 1) 2 2( , )1 2 1 2 k kB k k     …… ………… 8 分 由题意得： 2 2 2 2(2 1) 2 2( , )1 2 1 2 k kC k k    2 2 2 2 2 1 2 2(2 1) 21 2 AC k kk k k k      …… ………… 9 分 数学试卷 第 12 页 共 4 页 （注：因为直线 AB 与直线 AC 关于 x 轴对称，所以 ACk k  也可） 所以直线 AC ： ( 2)y k x   ，令 0x  ，则 (0, 2 )P k …… ………… 10 分 (注：写出 P 点坐标才给分) 2 2 2 2(2 1) 2 2( 2, 2 ) ( , 2 )1 2 1 2 k kPA PB k kk k          4 2 2 4 10 2 1 1 2 2 k k k    …… ………… 12 分 （注：写出向量坐标，没整理对给 1 分） 即 4 28 18 5 0k k   …… ………… 13 分 解得： 2 5 ( )2k   舍 2 1 4k  …… ………… 14 分 所以： 1 2k   直线l ： 2 2 2 xy   或 2 2 2 xy    …… ………… 15 分 19. （本小题满分 15 分） （Ⅰ）设等比数列 na 的公比为 q.由 1 3 21, 2,a a a   可得 2 2 0q q   .因为 0q  ，可得 2q  ， …… ………… 1 分 故 12n na  . …… ………… 2 分 设等差数列{ }nb 的公差为 d，由 4 3 5a b b  ，可得 1 3 4.b d  由 5 4 62a b b  ，可得 13 13 16,b d  数学试卷 第 13 页 共 4 页 从而 1 1, 1,b d  …… ………… 3 分 故 .nb n …… ………… 4 分 所以数列 na 的通项公式为 12n na  ，数列{ }nb 的通项公式为 .nb n （Ⅱ） （i）        ,3,2 ,33,1 1 1 kk kk n n nc …… ………… 5 分 )1()1( 333  nabcb nnn …… ………… 6 分 nnnn 363)12(3 11   …… …………7 分 （ii） 1 2 2 2 )2)(1( 2 )2)(1( 11    nnnn n nn na nnn n . …… ………… 8 分 13 2 23 2 4 4 5 8 3 2 4 4 2 1 3 2 133 3   nnT nn n  …… ………… 9 分 （注：先求 nT 再求 3nT 也没问题） 2 1 23 23 3  nT n n …… ………… 10 分    nnnn i i i iii i ii i ii bcbbcbcb 3 1 3 1 3 1 3 1 1-)1-( ）（）（ …… ………… 11 分    n ii i i n i bcb 3 11 33 )1( 数学试卷 第 14 页 共 4 页 3 1 1 1 3 1-6 ) 3 (1 3 ) (1 3 ) 3(3 6 3 ) 1-6 1 3 2 n n n n nn i i i i i               （ （等比求和 1 分，等差求和 1 分） …… ………… 13 分 2 323 10 96 2 3)31( 2 )1-3(3 5 )1-63 21 nnnnnnn  （ … ………… 14 分 （注：写成 3 3 3 3 3 1 1 1 1 n n n i i n n i i i i i i i bc b b b c           (1 3 ) 3 3 (1 3 ) 3 1-6 ) 2 1 3 1-6 n n n n       （ 1 26 9 3 2 3 10 2 n n n     没问题 ） 2 329 10 46 23 8 13 1 3 nnnn i iin ncbT n     …… ………… 15 分 （注：结果对即可如） 20. （本小题满分 16 分） 解：（Ⅰ）因为 2ln( ) 1 x af x x x     所以 ( ) ( ) 2 lng x xf x x x a    …… ………… 1 分 (0, )x  2( ) xg x x   …… ………… 2 分 x (0,2) 2 (2, ) ( )g x 负 0 正 ( )g x 单调递减 极小值 单调递增 数学试卷 第 15 页 共 4 页 (注意：没有列表，写清楚导函数符号单调性不减分，没有写导函数符号直接出单调区间减 1 分) …… ………… 3 分 所以 ( )g x 单调递减区间为 (0,2) ，单调递增区间为 (2, ) 极小值为 (2) 2 2ln 2g a   , 无极大值. …… ………… 4 分 （Ⅱ） ( ) lnh x x a x  有两个零点. 因为 ( ) 1 a x ah x xx     所以 …… ………… 5 分 ①当 0a  时， ( ) 0h x  ， ( )h x 单调递增，不可能有两个零点； …… ………… 6 分 ②当 0a  时，令 ( ) 0h x  ，得 0 x a  ， ( )h x 单调递减； 令 ( ) 0h x  ，得 x a ， ( )h x 单调递增. …… ………… 7 分 所以 min( ) ( ) lnh x h a a a a   要使 ( )h x 有两个零点，即使 ( ) 0h a  ，得 ea  ， .…… ………… 8 分 又因为 (1) 1 0h   ，所以 ( )h x 在(1, )e 存在唯一一个零点 …… ………… 9 分 且 ea  ，   2e e 0a ah a   ， 所以 ( )h x 在 e,ea 上存在唯一一个零点，符合题意. …… ………… 10 分 综上，当 a e 时，函数 ( )h x 有两个零点. 法二： ( ) lnh x x a x  有两个零点， 等价于 1 ln xx x  时，a 有两个实根，（1） …… ……5 分 令 ( ) ln xF x x  2 ln 1( ) ln xF x x   …… ……6 分 当 (0,1)x 时， ( ) 0F x  ， ( )F x 单调递减，且 ( ) 0F x  ； …… ……7 分 当 (1, )x e 时， ( ) 0F x  ， ( )F x 单调递减； 数学试卷 第 16 页 共 4 页 当 ( , )x e  时， ( ) 0F x  ， ( )F x 单调递增；…… ……8 分 ( )F e e ， 1 , ( )x F x   ， , ( )x F x    …… ……9 分 要使（1）有两个实数根，即使 ( )a F e e  ， 综上，当 a e 时，函数 ( )h x 有两个零点. …… ……10 分 （Ⅲ）   e (ln ) e ln e 0x x xx a x x x a x x     有两个实根， 令 ext x ， ( ) lng t t a t  有两个零点 1t , 2t , 1 1 1ext x ， 2 2 2ext x 所以 1 1 2 2 ln 0 ln 0 t a t t a t      …… …………11 分 （注意：上来没有直接换元，写 1 2 1 1 1 2 2 2 (ln ) 0 (ln ) 0 x x x e a x x x e a x x        给 1 分） 所以  2 1 2 1ln lna t t t t   （1）  2 1 2 1ln lna t t t t   （2） …… …………12 分 （注意：写 2 1 2 1 2 1 2 2 1 1 2 1 2 2 1 1 (ln ln ) 0 (ln ln ) 0 x x x x x e x e a x x x x x e x e a x x x x              给 1 分） 要证 1 2 2 1 2 ex xe x x   ，只需证   1 2 2 1 2e e ex xx x  ，即证    1 2 1 2ln e ln e 2x xx x  ，………13 分 所以只需证 1 2ln ln 2t t  . 由（1）（2）可得   2 2 1 12 1 2 1 2 1 22 1 1 1 ln ln ln ln ln 1 t t t tt tt t t t tt t t          ， 数学试卷 第 17 页 共 4 页 只需证 2 2 1 1 2 1 1 ln 2 1 t t t t t t       . …… …………14 分 设 1 20 t t  ，令 2 1 tt t  ，则 1t  ，所以只需证 1ln 2 1 tt t   ，即证 4ln 2 01t t    . 令 4( ) ln 21h t t t    ， 1t  ，则 2 2 2 1 4 ( 1)( ) 0( 1) ( 1) th t t t t t       ， …… …………15 分 ( ) (1) 0h t h  . 即当 1t  时， 4ln 2 01t t    成立. 所以 1 2ln ln 2t t  ，即   1 2 2 1 2e e ex xx x  ， 即 1 2 2 1 2 e ex xx x  . …… …………16 分